基于锈蚀模型的钢闸门动力性能研究

张晓臣

（中国水利水电第十一工程局有限公司,河南 郑州 450001）

1 引言

水工钢闸门在整个水利枢纽中扮演重要的角色,它是开启和关闭泄水通道的重要部位,它拦截水流、控制水位、调节流量,必要时还要进行排放泥沙。钢闸门的损坏引发事故的案例目前已经有很多,对于水工钢闸门来说,因其材料都为钢材,锈蚀是对钢结构性能影响的重要因素,由于钢闸门几乎都处在潮湿、干湿交替、被水流冲刷、水生物腐蚀的环境中,极易发生化学腐蚀,导致闸门的刚度、强度以及动力学性能发生变化,使其不具备良好的性能,因此对钢闸门锈蚀后性能的研究是非常有必要的,不仅如此对于现役钢闸门进行定期检测和维护也是十分有必要的。

闸门锈蚀后,锈蚀部件的截面尺寸都会减小,这将会引起闸门强度、刚度和稳定性发生变化,使其变形增大,力学性能减退,导致闸门的使用寿命降低,从安全的状态转变为不安全的状态,因此锈蚀是水工钢闸门运行中必不可少的一个需要考虑的要素[1-2]。

另外,锈蚀对闸门的自振频率也有一定的影响。水体的自振频率较多为低阶频率,当闸门发生锈蚀以后,自振频率会发生改变,可能会与水体相近,这个时候就会引起共振,导致闸门的振动幅值增加,当幅值大到一定程度的时候,就将引起闸门的振动破坏。为了更加贴进实际情况,应考虑在流固耦合的情况下来研究锈蚀对闸门自振频率的影响。

2 流固耦合理论

流固耦合是同时研究流体和固体之间相互作用的一门交叉学科,在动水作用下,流体与闸门会有耦合作用,流体对闸门具有一定的影响,即可能会导致闸门的振动特性发生一定的变化。因此,要充分考虑流体的作用,此时的运动方程为：

式中：[Ms]为闸门的质量矩阵；[Cs]为闸门的阻尼矩阵；[Ks]为闸门的刚度矩阵；[Mf]为水流作用的附加质量矩阵{u}为节点加速度列向量；{u}为节点速度列向量；{u}为节点位移列向量；{Ff}为水流引起的荷载向量；{Fs}为闸门结构上的其他荷载向量。

最终得到考虑水流影响闸门系统的特征方程为：

3 钢结构锈蚀计算模型

徐善华教授[1]提出锈蚀后钢材弹性模量与屈服强度的计算模型,在锈蚀弹性性能的测试中引入了细观力学概念,建立了相关计算模型,并进行相关实验,最后得到含有表面锈蚀坑损伤的材料等效体积模量：

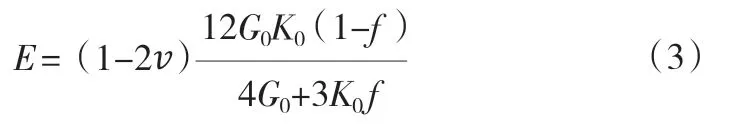
式中：v 取0.25；K0为120 GPa；G0为72 GPa；f 为锈蚀损失率,即为锈蚀材料质量与未锈蚀前质量之比。

将以上各参数带入（3）可以得到：

通过该弹性模量计算公式,得出锈蚀后的等效弹性模量,即可对闸门锈蚀后的动力性能进行研究。

4 实例分析

本文采用ANSYS 对平面钢闸门锈蚀后的动力性能进行研究。以某水利工程的平面钢闸门为例,闸门形式为直升式,进水口检修闸门为平板定轮钢闸门,闸门总体高度为4.68 m；闸门结构类型为板梁结构,布置方式为登高等高布置,主横梁则为截面组合梁,每节门均有2根主横梁,整扇闸门共4根；纵梁为焊接T 形截面组合梁,共3根；小横梁为∠100×65的角钢,共4根；顶、底梁均为20 号槽钢。

闸门使用40年后的锈蚀情况经过检测由表1给出。

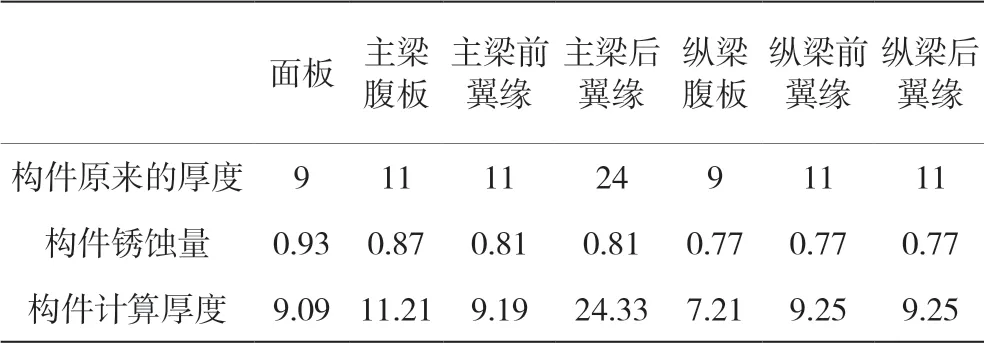
表1 闸门主要构件锈蚀量和锈蚀速率的平均值 单位：mm

采用ANSYS APDL 来建立有限元分析模型,其中：x 轴垂直水流方向,指向右方表示正向；y 轴顺水流方向,指向下游则表示正向；z 轴铅直向上,零点位于闸门左侧角点处。约束条件取为：底面采用竖向链杆约束,支铰较轴采用轴向链杆约束,闸门侧向链杆约束。

建立闸门模型,所有构件均采用shell181 单元,水体单元采用fluid30 单元。考虑水体作用,为了能够更加贴近实际情况,选取水体的长度为4 倍闸门的宽度来模拟。整个有限元模型共有483213 个单元,504210 个节点。考虑锈蚀影响一般采用生死单元来进行模拟,而本文引入了基于锈蚀后弹性模量计算模型,通过采用弹性模量的等效来模拟锈蚀的情况。比较在设计水头下,闸门非锈蚀情况和锈蚀情况下的动力性能,以及在锈蚀状态下,不同的水位情况下,闸门的动力变化。模型见图1。

图1 水工钢闸门有限元分析模型

通过考虑流固耦合作用对闸门动力性能进行分析,提取前6 阶振型。通过给出的监测数据,可以计算出锈蚀损失率。然后将锈蚀损失率带入到（4）中,即可求出闸门使用40年后的等效弹性模量E=1.47×105Pa,将未锈蚀状态下的弹性模量用该弹性模量替代后计算即可得到闸门锈蚀后的动力特征。具体见图2。

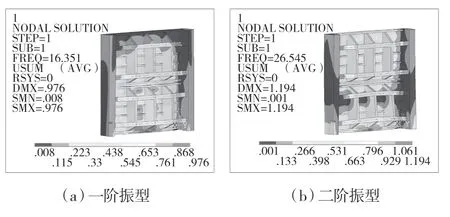
图2 闸门锈蚀后在设计水位下的自振频率

在设计水位时,闸门锈蚀状态和未锈蚀状态的自振频率见表2。

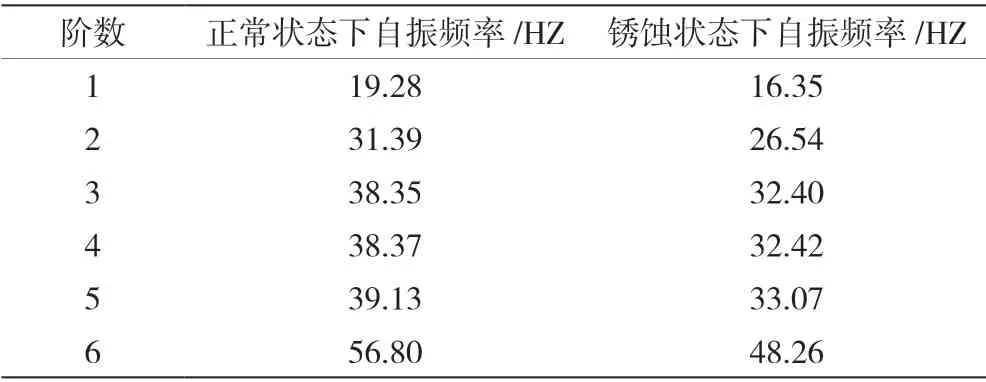
表2 闸门设计水位时两种状态下自振频率

图3 设计水位两种状态闸门自振频率比较

对比在设计水位时锈蚀闸门和非锈蚀闸门的振型,可知当闸门锈蚀之后,自振频率降低。无论是闸门在锈蚀还是非锈蚀状态下,闸门在门前有水且全关的状态下,由于底部受到约束的影响,门体总体的振动幅度不大,主要振型特征为被水面空间联接系的摆动。在低阶次下,背水面空间联接系振型比较明显。

表2和图2表示在锈蚀以及非锈蚀状态下闸门结构的振动频率,根据表2可以看出,闸门在锈蚀状态下的振动频率出现了明显下降,并且前六阶自振频率降幅都在15%左右。结果显示闸门在锈蚀后,振动情况会有显著的变化。闸门长期在水中关闭和开启,由于电化学反应的存在,导致闸门发生了锈蚀,进而引起锈蚀部分材料的退化,导致强度变低,所以闸门的自振频率相应降低。因此闸门的锈蚀问题值得进一步重视。

由上述可知,当闸门使用40年锈蚀后自振频率几乎稳定的以15%左右的降幅下降,但闸前水位是动态变化的,因此为了研究不同水位对锈蚀闸门的影响,取依次降低的水位进行模拟,来研究不同水位对锈蚀闸门的影响。计算结果见图4。

图4 水位为4.14m 时锈蚀闸门自振频率

当锈蚀状态下的闸门在不同水位下,自振频率见表3。

表3 水位为4.14 m 两种状态的闸门自振频率

通过表3可以得出,当水位在逐渐降低的过程中,锈蚀后的闸门每一阶振型所对应的自振频率在逐渐增大并且在不同水位的作用下,闸门以面板和横隔板的振动为主,其中从图5中可以看出不管处于什么水位,对边梁的自振频率影响非常小,几乎都在同一个值附近稍微波动。闸门未锈蚀的情况下,随着水位的升高而自振频率减少,当闸门拦蓄水流时的水位高时,在此高水位状态下,自振频率将降低得更快并且如果闸门出现了锈蚀,那么共振的机会将会大大增加,导致闸门运行不稳定。因此对于高水位的闸门,应该重点关注锈蚀作用对闸门的影响。

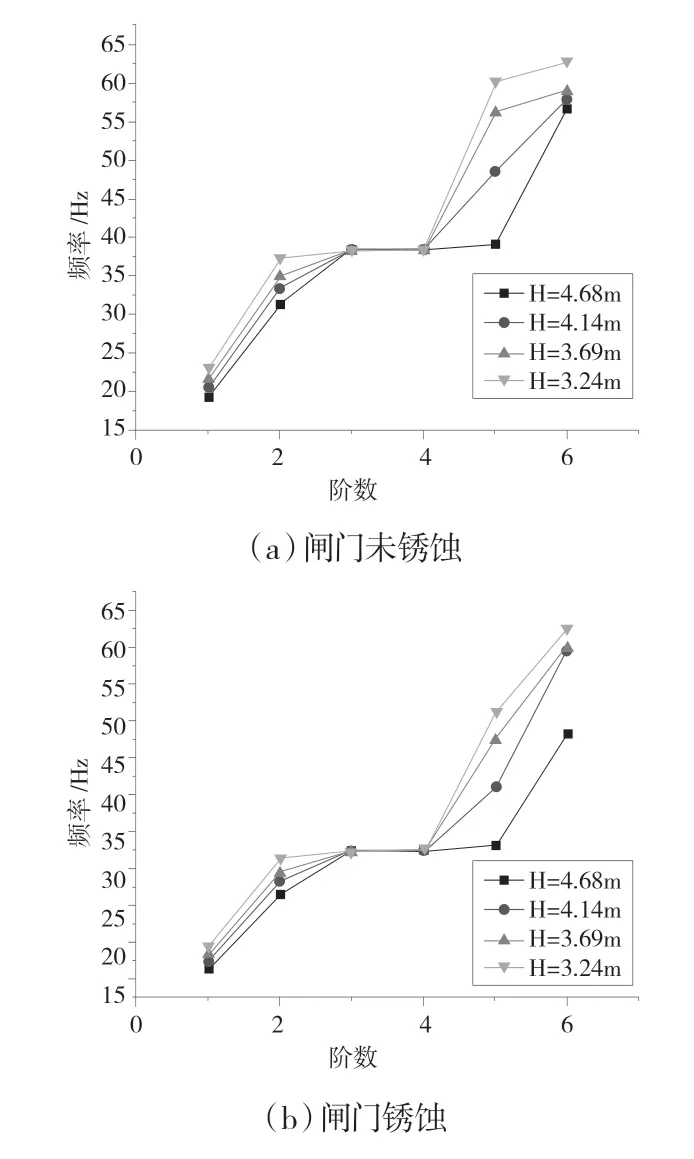
图5 不同水位下闸门自振频率

5 结论

（1）采用等效替代的弹性模量来模拟计算锈蚀的闸门动力特性,规律性较好。等效替代的弹性模量从细观力学的角度出发,建立锈蚀损伤模型,通过进行严格的推导,得出了等效弹性模量的计算公式,该方法简化了对锈蚀的计算,通过引入锈蚀损失率来进行求解。

（2）水工钢闸门在水流的影响下,振动主要以低频的振动为主,当闸门出现锈蚀之后,材料性能减弱,截面尺寸削弱,导致闸门整体刚度变小,从而自振频率降低。

（3）通过选取不同的水位进行模拟,随着水位的逐渐升高,闸门的自振频率在逐渐的减小,若闸门锈蚀后,则自振频率将会降低更快,但边梁的振动受水位的影响不大,因此主要对锈蚀后闸门的面板和梁结构进行加固。