面向6G通感算融合的多粒度资源分配算法

金仙美，王佳妮，赵力强， 朱伏生

(1.西安电子科技大学 通信工程学院，陕西 西安 710068;2.广东省新一代通信与网络创新研究院,广东 广州 510700)

0 引言

随着信息技术的发展，接入互联网的流量大小 与移动网络应用场景数量都在飞速增长[1]。多样化的业务场景对时延、可靠性、带宽、接入数量等通信需求越发严苛，数目激增的无线通信和IoT设备导致用户需求和无线资源与算力资源之间的矛盾愈发突出。现有的资源分配模式单一，且缺少用户行为感知，难以精确刻画业务需求变化趋势，导致运营商提供的网络服务质量和网络管理质量下降[2]。解决问题要求运营商实时感知网络状态，预测用户需求变化，提前调配、预留网络资源，避免资源紧缺现象发生。因此需要设计面向6G(6th Generation Mobile Communication System)网络的通感算融合资源分配算法，实现无线资源精确、按需分配，提高网络资源利用率的同时保证用户的服务质量(Quality of Service，QoS)。

而无线接入网中，网络环境复杂多变，网络中的资源种类繁多，但资源总量有限[3]，传统的基于数学模型的网络优化方法不再适用[4-6],因此算力、存储以及网络资源分配问题得到许多研究人员的关注。其中深度强化学习(Deep Reinforcement Learning，DRL)算法可以通过与未知环境交互来实现系统性能的自我优化，从而受到极大的研究关注[7-9]。文献[10]使用几种DRL算法敏锐地捕捉来自不同切片的用户需求，从而产生资源分配策略，并在平台上实施和评估这些算法，验证所研究方法的优越性能。为使资源分配更加精细化，有研究者提出基于多时间尺度的资源分配方法。文献[11]提出一个分层DL框架，在每个长时隙中，服务提供商采用DRL算法来确定切片配置参数，在每个短时隙和小时隙中增强移动带宽(Enhanced Mobile Broadband，eMBB)和低时延高可靠通信(Ultra-Reliable Low-Latency Communications，uRLLC)调度器使用DNN算法分别将无线资源分配给相应的用户。文献[12]中也提出一种双层控制粒度的智能无线接入网(Radio Access Network，RAN)切片策略，旨在最大化服务的长期QoS和切片SE，其中上层控制器通过业务流量的动态变化自适应调节切片配置以确保QoS性能，而下层控制器在小时间尺度上给用户分配无线资源来提高切片的SE。但是上述资源分配算法没有考虑频繁调整资源分配策略带来的损耗问题。

综上，常见的资源分配算法均只考虑在同一时间粒度内对资源进行调整，资源管理粒度单一，难以应对高度复杂的场景建模，随后衍生出双时间尺度资源分配算法。双时间尺度的资源分配算法在两个不同的层面分别采用大尺度的粗粒度资源管控和小尺度的精细化资源调配，对资源的管理更加高效方便。但在无线通信的实际应用场景中，基站内资源分配操作的更新，需要耗费基站本身的计算资源。因此，适当的改进资源调整的频率，在多时间粒度上给基站和用户的资源进行调整，可以减少调整资源的成本，从而缓解算法在实际场景中占用资源较多的问题。

针对上述面临的一些复杂的无线接入网智能感知与资源分配问题，提出一种面向6G通感算融合的多粒度资源分配算法。将RAN中的通信、感知、计算资源联合优化问题建模为最大化效用函数问题(即所有用户的时延、频谱效率以及调整资源成本的加权和)，并满足用户所能容忍的最小数据传输速率、所有用户与基站占用的资源不超过系统总资源等约束，进而获得最优的资源分配策略。

1 系统模型

对于用户的感知信息(用户未来流量、业务类型)，采用常用的方法进行感知。文中对流量的预测包含用户的流量预测和基站的流量预测，统称为流量预测，采用多步预测的Seq2Seq模型，由于其内部存在编码器和解码器两部分，可以更好地表征历史数据特征并且用此特征进行未来数据的预测。在业务估计方面采用的卷积神经网络(CNN)自动提取流量数据特征进行业务估计。本文重点在于利用流量预测与业务估计的结果实现基于通感算融合的多粒度资源分配算法，下面重点说明对多粒度资源分配算法的建模。

1.1 数据传输模型

时间维度被划分为多个传输时间间隔(Transmission Time Interval，TTI)，某一时间间隔被记为t∈{0,1,2,3,…,T}，T为资源分配策略中的最大有效时间长度。共有N个用户设备与基站之间通过无线链路进行信息传输，某一用户设备被记为n∈{1,2,3,…,N}。则用户n在某一时间间隔t内占用的带宽资源表示为：

Bn,t=1.8×105×en,t,

(1)

式中，en,t为基站在某一时间间隔t内分配给用户n的RB数量，而每个RB所占用的带宽为180 kHz。

在时间间隔t内用户n与基站之间的信噪比(signal-to-Noise Ratio，SNR)可以定义为：

(2)

式中，σ2为加性高斯白噪声功率，gn,t为用户n与基站相连接的无线信道在时间间隔t内的信道增益，pn,t为无线信道的发射功率，那么基站在时间间隔t内向用户n传输数据的速率可以表示为：

(3)

(4)

1.2 基站计算模型

基站处理数据的速率也是影响用户QoE的一个重要因素，而基站处理数据的速率与基站的计算资源有关。因此，本节对基站的计算过程进行建模。

基站在某一时隙t内的计算速率定义为：

(5)

式中，ωt为基站分配的计算资源，单位为cycles/s，φBS>0表示基站处理一位数据流所需的计算周期，单位为cycles/bit，由应用程序的属性决定，假设该值为一个定值，不会随时间的变化而变化，则基站在时间间隔t内处理所有数据的时延可以表示为：

(6)

式中，ft为基站在某一时间间隔t内需要处理的数据量大小，为所有用户的流量之和。

1.3 用户QoE建模

记基站在时间间隔t内发送给某一用户设备n的数据量为fn,t，则下一个时间间隔t+1内基站需要发送给用户n的流量可以表示为：

(7)

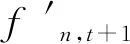
(8)

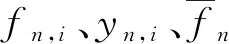
数据流从基站侧传输到用户端的时延包括传输延迟和基站处理延迟两部分，其中传输时延由基站与用户n之间的数据传输速率决定，而基站处理时延由基站的计算资源决定。在本节所述的系统模型中，时延被定义为传输时延和基站处理时延的总和。因此，数据流从基站传输到用户端n的总时延被建模为：

Dn,t=μt+δn,t,

(9)

式中，μt为基站处理时延，δn,t为传输时延。当基站需要传输到用户端的数据流较小时，基站处理时延接近于0，此时，Dn,t主要由传输时延决定；当基站需要传输到用户端的数据流较大时，Dn,t主要由基站处理时延和传输时延共同决定。

1.4 优化问题建模

本文所提算法与其他资源分配算法的不同之处在于考虑由于实时调整资源分配策略而造成的资源损耗问题，并将该问题转化为一个多时间粒度资源分配问题，多时间粒度体现在算法所生成策略的有效作用时间，尽可能减少资源调整的次数。本文通过调整两次资源调整之间的时间间隔实现资源调整频率的降低，而该时间间隔的大小是由资源分配算法本身所决定的，与当前以及未来的环境状态有关，是一个不确定的值，也就是在多个时间粒度上进行资源分配，不是以固定的频次分配资源，即多粒度资源分配。所设计的资源分配算法在状态Si下进行第i次决策时所产生的资源分配策略Ai中不仅包含多种资源分配的数值大小，也包含这些资源的有效作用时间τi，其中Si与Ai将在下一节进行详细介绍。本节从用户的QoE、SE和执行动作的成本三个角度出发构建系统的效用函数，可表示为：

(10)

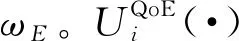
(11)

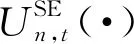
(12)

式中，βn,t,1,β2分别为数据流总时延和平均SE的权重因子，η为资源调整成本的权重因子，表示这三个量在效用函数中的重要性。由于不同的业务对时延需求不同，因此权重因子βn,t,1在用户访问不同的业务时所取的值也不相同。对于用户的业务估计采用常用的CNN进行。

本文的目标是获得最优的RAN资源分配策略，该策略能够在满足资源调度约束的同时，最大化系统的效用函数，总结如下：

maxUi(Si,Ai)

C4:ωt+ωE<ωmax,∀t∈τi,

(13)

2 基于Dueling DQN的多粒度资源分配方案设计

决斗深度Q网络(Dueling Deep Q-network，Dueling DQN)算法是DQN算法的改进版。两者的主要区别在于所采用的用于拟合Q函数的神经网络结构不同，如图1所示。

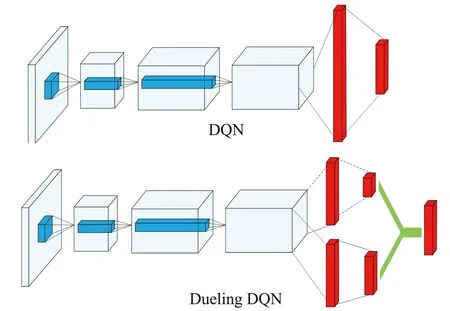
图1 DQN算法与Dueling DQN算法Q网络结构对比图

DQN算法中采用Q网络由三个卷积层以及两个全连接层构成，DQN的Q网络是单流的，该网络结构只考虑在当前状态下采用哪个动作可以获得最大的奖励值。而Dueling DQN算法中采用的Q网络是双流的，分别表示状态值函数和动作优势函数，利用汇聚的两种状态函数拟合Q函数，该网络结构着重关注重要状态，忽略不重要状态，因此收敛速度更快，更容易寻找最优策略。

根据Dueling DQN算法的网络结构，状态值函数可以表示为Vπ(Si;θ,ξ)，动作优势函数可以表示为Aπ(Si,Ai;θ,α)。其中，θ为三个卷积层的网络参数，ξ表示状态值函数的全连接层的网络参数，α表示动作优势函数全连接层的网络参数，为得到唯一的V(Si;θ,ξ)和A(Si,Ai;θ,α)，得到Q函数为：

Q(Si,Ai;θ,α,ξ)=V(Si;θ,ξ)+

(14)

由于DQN算法架构均需要构建状态集、动作集以及奖励函数，因此根据本文的场景，将分别介绍这三者在本文中的定义。

(1) 状态集定义

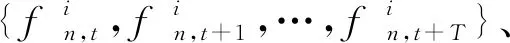
(15)

所以，本系统的状态集可以表示为：

S={S1,S2,…,Si}。

(16)

(2) 动作集定义

在本文所构建的模型中，资源分配算法需要求解出基站所需的计算资源、基站为每个用户分配的RB资源和发射功率资源。因此每一次动作Ai包含需要分配的各种资源的数值大小以及资源分配结果的有效作用时间，可以表示为：

(17)

(3) 奖励函数

在强化学习中奖励值越大，代表选择的策略越符合优化目标。在本节中，目标是在满足约束的同时最大化系统效用函数值。所以系统效用函数值越大，策略获得的奖赏越大，奖赏可以表示为：

R(Si,Ai)=Ui(Si,Ai)。

(18)

DQN的目标在于求解出累积奖赏最大时所对应的策略，表示为：

(19)

式中，Q(Si,Ai)是一个无限期折扣报酬，λi是一个折扣因子，当i足够大时，λi趋近于零。

在状态Si下采取行动Ai是一个马尔科夫过程，根据马尔科夫状态转移的过程可知，下一个状态Si，与之前的状态均无关，仅仅与此刻的状态以及所采取的行动有关，因此Q函数的更新可以为：

Q(Si,Ai)→Q(Si,Ai)+ψ(R(Si,Ai)+

λmaxQ(Si，,Ai，)-Q(Si,Ai))，

(20)

式中，ψ为学习率。

在Dueling DQN算法中包含两个与Q函数相关并且结构相同的DNN，其中一个DNN用于拟合Q函数的值，被称为评估Q网络，表示为：

Q(Ai,Si;θ,α,ξ)≈Q*(Ai,Si),

(21)

式中，θ为评估Q网络中设定的三个卷积层的网络参数，ξ表示评估Q网络中状态值函数全连接层的网络参数，α表示评估Q网络中动作优势函数全连接层的网络参数。另一个DNN用于得到目标Q值，被称为目标Q网络，表示为：

(22)

式中，θ-为目标Q网络中设定的三个卷积层的网络参数，ξ-表示目标Q网络中状态值函数全连接层的网络参数，α-表示目标Q网络中动作优势函数全连接层的网络参数。

在学习阶段，会将随机抽样的样本(Si,Ai,R(Si,Ai),Si，)存放到经验池中，只有当经验池中所存储的样本数量大于随机抽样的样本数量时才开始训练。在训练阶段，agent从经验池中随机抽取小批量样本(si,ai,r(si,ai),si，)，将si作为评估Q网络的输入，(r(si,ai),si，)作为目标Q网络的输入。在每一步训练中，Dueling DQN都通过最小化损失函数的方式对两个DNN的参数进行更新，损失函数可以表示为：

将从经验池中抽取的样本输入到评估Q网络中计算该网络参数θ对应的梯度θ，再使用Adam算法对网络参数θ进行更新。并每隔一段时间将评估Q网络的参数〈θ,α,ξ〉直接赋值给〈θ-,α-,ξ-〉，实现目标Q网络参数更新。整体算法流程如算法1所示。

算法1 基于Dueling DQN的多粒度资源分配算法输入:动作集A,奖励衰减因子λ,经验池K的最大容量,最大允许误差ε,更新参数的样本批次,目标Q网络参数<θ-,α-,ξ->更新间隔Z。输出:最优策略,满足用户QoS条件下,得到资源分配的结果以及资源分配的有效时间所组成的最佳动作序列。1. 初始化:经验池K,评估Q网络参数<θ,α,ξ>,目标Q网络参数<θ-,α-,ξ->=<θ,α,ξ>。2. 初始化存储空间3. Step = 04. for episode = 1,2,... do5. for t= 1,2,... do6. 初始化网络状态Si;7. agent的Q网络使用状态Si作为输入,输出所有动作对应的Q值,根据公式π*从所有Q值中选择动作Ai;8. 将agent所选定的动作Ai输入环境中执行,然后获得R(Si,Ai)以及下一个状态Si,;9. agent将经验(Si,Ai,R(Si,Ai),Si,)存入经验池D中;10. Si←Si,;11. if Step > 10012. 从经验池K中随机抽取G个样本(si,ai,r(si,ai),si,)进行训练;13. 利用DNN计算Q值,用式(4)～(22)计算损失函数,并使用Adam算法对评估Q网络参数<θ,α,ξ>进行更新;每迭代Z步后,进行一次操作;14. end if;15. Step += 1;16. end for17. end for

3 平台部署与方案验证

本小节搭建的长期演进(Long Term Evolution，LTE)实验平台均借助开源软件实现，并且全部网元、算法实现等都部署在Docker容器中，统称为网络功能(Network Functions，NFs)，从而实现网络功能的虚拟化，然后由Kubenetes对这些NFs进行统一管理。

3.1 平台部署

平台所需的硬件环境包括三台x86通用服务器、一个NETGEAR开放虚拟交换机(Open vSwitch，OVS)型号为MT7621AT、一个通用软件无线电外设(Universal Software Radiio Peripheral，USRP)型号为USRP210、三个用户手机型号为华为Mate7。其中三台通用服务器分别用作CNN、SequentialSeq模型的训练与在线推理，实现网络感知；部署开源软件LTE无线接入网OAI-eNB和FlexRAN，实现无线接入网控制面与用户面；部署开源OAI软件核心网。

FlexRAN，用于给用户分配无线资源；Docker，用于承载各个面中每个虚拟化后的NFs，对服务器底层的硬件资源进行虚拟化处理，保证各个NFs能够正常工作；Python，主要用于感知面、智能融合面中各种与AI相关的网络功能的开发与实现；Nginx，用于搭建相关业务的服务器，满足用户对业务多样性的需求。

由于受到软硬件条件的限制，无法针对每个用户调整发射功率，因此在将算法部署到实验平台中时对其进行一定的简化。将资源分配算法部署在Dockers容器中。当该节点中所有的pod从containerCreating到running状态后即说明K8s集群以及基于网络智能感知的多粒度资源分配算法平台已经部署成功。

3.2 方案验证及结果分析

本节中基于深度强化学习的多粒度资源分配算法的参数配置主要根据经验进行选取,学习率为0.001，折扣因子为0.95，经验回放为5 000，随机采样样本数为128，更新频率为100，迭代次数为8 000。考虑到流量采样时间对流量预测与业务估计的影响，实验验证在保存完整流量信息的流量采样时间为1 s和10 s的情况，在结果图中用括号标注。

3.2.1 资源分配算法对频谱效率的影响

图2对比用户在访问电子书业务时采用不同分配算法对频谱效率的影响。

从图2(a)可以看出，采用平均分配算法时频谱效率只达到2.4 bit·s-1·Hz-1，而采用其他两种资源分配算法为用户分配RB资源时频谱效率可达3.2 bit·s-1·Hz-1左右。此外，采用基于网络智能感知的多粒度资源分配算法的频谱效率与单粒度接近。

从图2(b)图中看出，采用平均分配算法时频谱效率只达到2.4 bit·s-1·Hz-1，而采用其他两种资源分配算法为用户分配RB资源时频谱效率可达3.2 bit·s-1·Hz-1左右；同样，采用基于网络智能感知的多粒度资源分配算法的频谱效率与单粒度接近。

(a) 流量采样时间为1 s

导致以上结果的原因是平均资源分配方法给每个用户都分配15个RB资源，在用户下载电子书时RB资源非常充足，因此频谱效率较低，而其他两种资源分配算法综合考虑业务的时延和频谱效率两个因素，因此频谱效率较高。但是，由于基于网络智能感知的单粒度资源分配算法在每个TTI内都会执行一次资源分配动作，可以根据网络和资源状况灵活调整资源分配策略，而基于网络智能感知的多粒度资源分配算法每隔几个TTI才会重新执行一次资源分配动作，因此，基于网络智能感知的单粒度资源分配算法的频谱效率比较稳定。

3.2.2 不同分配算法对总时延的影响

图3对比采用不同资源分配算法后对数据传输总时延的影响。定义总时延为基站处理数据的时延与数据通过无线信道传输时的时延之和。图3(a)为流量采样时间为1 s的情况下流量传输所产生时延的累计概率分布图，可以看出，当采用平均资源分配算法时，只有一部分业务流量可以在1 s以内到达用户端，而采用其他两种资源分配算法，大多数业务流量可以在1 s以内到达用户端，而且单粒度资源分配算法的时延总体上稍微小于多粒度资源分配算法。

图3(b)为流量采样时间为10 s的情况下流量传输所产生时延的累计概率分布图，可以看出，采用平均资源分配算法时，只有一部分业务流量可以在10 s内到达用户端，而采用其他两种资源分配算法，大多数业务流量可以在1 s以内到达用户端，并且两种算法相差不大。

(a) 流量采样时间为1 s

这是由于采用平均资源分配算法时每个用户平均分配RB资源，当用户访问视频业务时会发生卡顿，造成传输时延增大，而其他两种资源分配算法会由于流量预测误差等因素，也会偶尔有RB资源分配不足的情况，造成传输时延稍微增大，但是本文所提出的算法根据基站所需发送的流量数据调整基站的计算资源从而降低处理时延，根据用户的未来流量调整用户的RB资源从而降低传输时延，因此总时延都小于平均资源分配算法。

3.2.3 不同流量采样时间对执行动作成本的影响

由于本文所提算法相较于其他资源分配算法，考虑基站执行资源分配动作时所消耗的成本，因此对相同建模下采用单粒度和多粒度资源分配算法的成本进行对比，如图4所示。

其中基站执行资源分配动作的成本使用perf工具进行测试。结合图2～图4可以看出，随着资源分配执行时间的增加，执行资源分配动作所耗费的成本越来越多，但是在频谱效率和总时延都达到类似性能的情况下，流量采样时间为1 s单粒度资源分配算法所耗费的成本远高于多粒度资源分配算法，流量采样时间为10 s单粒度资源分配算法所耗费的成本也高于多粒度资源分配算法，这是因为单粒度资源分配算法频繁更改资源分配策略所造成的。

图4 不同流量采样时间对执行动作成本的影响

3.2.4 用户的RB资源分配结果测试

本文中使用50 M带宽的LTE网络，以RBG(3个RB)[14]为单位给用户分配RB资源。图5和图6分别为在流量采样时间为1 s和流量采样时间为10 s的前提下基于网络智能感知的多粒度资源分配算法为用户分配的RB资源。

图5 用户的RB资源分配结果图(流量采样时间为1 s)

图6 用户的RB资源分配结果图(流量采样时间为10 s)

由图5和图6可以看出，当用户访问高清视频业务时，资源分配算法为其分配18个RB，当用户访问无损音乐时，资源分配算法为其分配3个RB，当用户访问电子书业务时，资源分配算法为其分配9个RB，均可以满足用户的需求。

3.2.5 流量预测精度对用户QoE的影响

QoE能够准确反映当前资源分配策略下用户的体验，而用户的QoE是由各项QoS综合后的结果，不能使用单一的指标描述各种业务的QoE[15]。有研究[16]针对视频业务给出常见的评估指标，如起始时延、卡顿次数等，本文将这些指标推广到本文所提供的高清视频、无损音乐和电子书业务，具体的评估指标定义如下文所述。

起始时延是指每项业务开始之前的持续时间。针对高清视频业务，是指从用户发出请求到视频开始播放的时间；针对无损音乐业务，是指从用户发出请求到音乐开始播放的时间；针对电子书业务，是指从用户发出请求到电子书内容展示在浏览器中经过的时间。

卡顿次数由于浏览器在业务开始前会将业务内容先放在缓冲区，只有当业务流填充缓冲区的速率大于或者等于业务播放的速率时，业务才不会发生卡顿。针对高清视频和无损音乐业务，是指视频或音乐在播放过程中发生卡顿的次数。针对电子书业务，是指电子书加载内容总量不变且持续时间大于2 s时发生的次数。

图7为流量采样时间为1 s的情况下，设置不同历史步长(H)和未来步长(T)的流量预测参数对业务平均起始时延的影响。从图中可以看出，无损音乐的平均起始时延最低，电子书的平均起始时延在0.5～1.9 s，高清视频的平均起始时延最高，在1.6～3.8 s，而且每种业务的平均起始时延大小与决定系数R2成负相关，即决定系数越大，该参数设置下的流量预测精度越高，资源分配策略越好，每种业务的平均起始时延越小。

(a) 历史步长为4 (b) 历史步长为6 (c) 历史步长为8

图8为流量采样时间为10 s的情况下，设置不同历史步长(H)和未来步长(T)的流量预测参数对业务平均起始时延的影响。从图中可以看出，无损音乐的平均起始时延最低，电子书的平均起始时延为0.8～2.4 s，高清视频的平均起始时延最高，为3.5～5.6 s，而且每种业务的平均起始时延大小与决定系数R2也成负相关。

(a) 历史步长为2 (b) 历史步长为4 (c) 历史步长为6

图9为流量采样时间为1 s的情况下，设置不同历史步长和未来步长的流量预测参数对业务平均中断次数的影响。从图中可以看出，无损音乐在播放过程中基本不会发生中断，电子书的平均中断次数在一次以下，高清视频的平均中断次数最高，而且每种业务的平均中断次数与决定系数R2成负相关，即决定系数越大，该参数设置下的流量预测精度越高，资源分配策略越好，每种业务的平均中断次数越小。

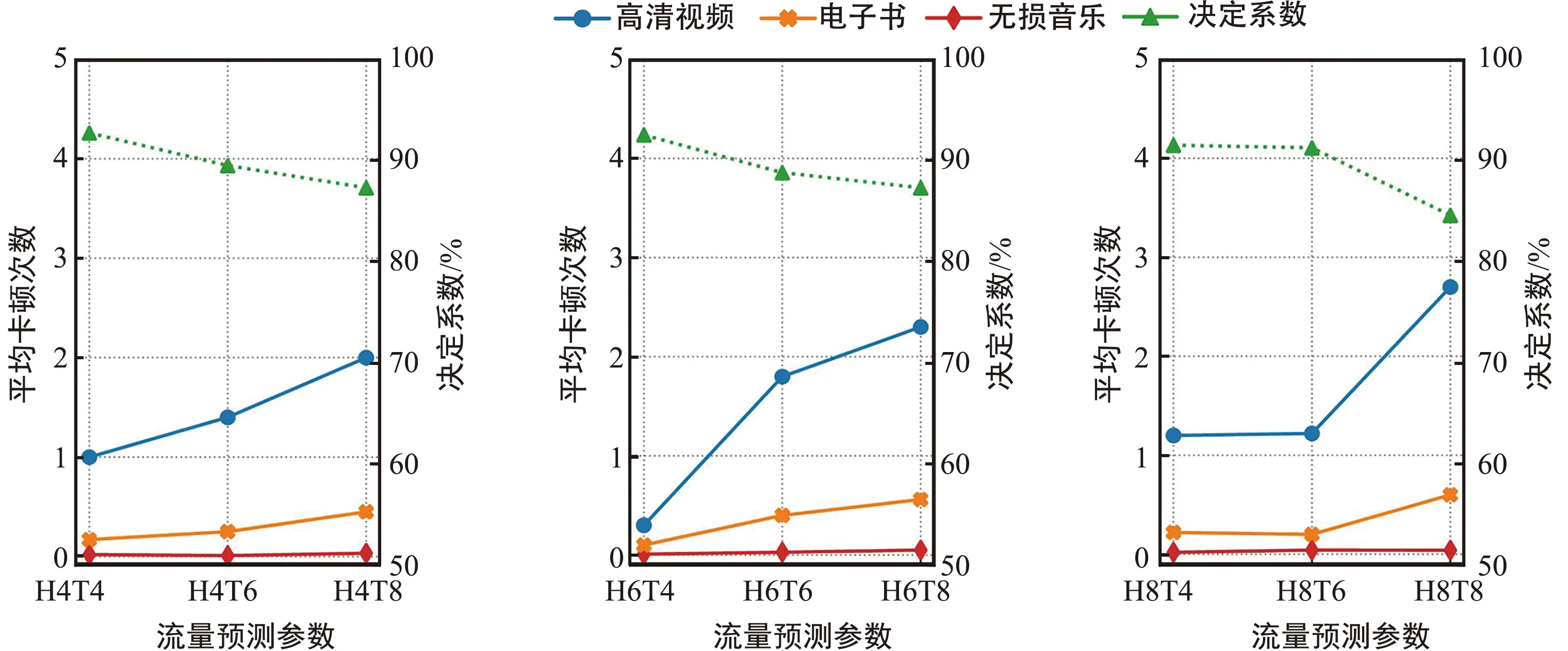
(a) 历史步长为4 (b) 历史步长为6 (c) 历史步长为8

图10为流量采样时间为10 s的情况下，设置不同历史步长和未来步长的流量预测参数对业务平均中断次数的影响。从图中可以看出，无损音乐在播放过程中基本不会发生中断，电子书的平均中断次数在2次以下，高清视频的平均中断次数最高，在3～6次之间。

(a) 历史步长为2 (b) 历史步长为4 (c) 历史步长为6

对比图7和图8、图9和图10可知，流量采样时间为1 s的用户QoE比流量采样时间为10 s的用户QoE好，这是由于流量采样时间越小，多粒度资源调整越精细，用户的QoE越好。

综上，实验结果证明，在面向6G通感算融合的多粒度资源分配算法可以满足用户QoE的情况下，本文算法能够提高网络频谱效率，并降低传输时延、处理时延和资源分配动作执行的成本。

4 结束语

本文提出一种面向6G通感算融合的多粒度资源分配算法，多时间粒度体现在算法所生成策略的有效作用时间。首先，将通信、感知、计算资源联合优化问题建模为多时间粒度上的最大化效用函数问题，并满足用户所能容忍的最小数据传输速率、所有用户与基站占用的资源不超过系统总资源等约束。其次，采用Dueling DQN算法对该问题进行求解，将感知信息(流量预测与业务类型估计结果)、通信信息(信噪比、发射功率、资源块数等)和计算信息(基站的计算资源)作为状态集；将资源分配策略有效作用时间粒度、资源块数、发射功率、基站的计算资源作为动作集；将所有用户的时延、频谱效率以及执行动作成本的加权和作为奖励值；最后，在基于开源软件搭建的实验平台中，将本文的算法与现有资源分配算法进行对比，验证本文所提的算法能够提高网络频谱效率，并降低传输时延、处理时延和资源分配动作执行的成本。