基于水文学法的沙颍河周口断面生态流量研究

张泽贤，檀 月，张钰萌，丁晓雯

(1.华北电力大学环境科学与工程学院，北京 102206；2.北京市排水管理事务中心，北京 100000)

1 概述

河流作为地球生命的重要组成部分、人类生存和发展的基础，对物质以及能量的运输与传递有重要影响作用。人们不合理地使用水资源，导致河流出现干枯、断流现象，生物多样性结构遭到破坏、生态系统发生退化现象[1]。河流生态系统一旦遭到破坏会难以恢复，因此河流应长期保持一定的基本水量即最小生态流量来维持自身健康发展。

目前，国内外河流生态需水量的计算方法[2]可分为：基于长序列历史流量数据进行计算，计算步骤简便，但精度较低的水文学方法；以研究断面的水力参数如宽度、流速等来计算生态流量并受河道断面影响较大的水力学方法；通过指示生物及其所需水力条件综合分析来确定生态流量的生境模拟法[3]；综合分析法是基于整体概念出发研究河流，涉及多个领域专家的共同研究，计算结果精度最高。采用水文学方法进行生态流量计算时只需依据多年历史流量资料，因此应用较其它3种计算方法更为广泛，并且适用于任何河流。生态流量的计算最先在美国西部得到应用，我国起步较晚，近年的研究多是基于原有方法进行改进并应用于实践。如Andrzej等[4]选用Tennant和Tessman方法对波兰杜纳耶茨河谷上的3条河流的生态流量进行了核算。栾清华等[5]采用细化到月尺度的基流比例法，根据年型、年际、年内的不同方面，分层次对洋河干流生态流量变化进行了解析，并评价了现状年河流生态基流的保障程度。林梦珂等[6]将改进年内展布法应用到渭河流域，将年径流过程分为汛期、非汛期两个过程计算生态基流，考虑了天然径流的季节性，减弱了极端天气对计算的影响，结果更加合理。周晓玉[7]以辽宁省下河套水库坝下河段当地的地理气候与河流特点为基础提出了一种改进Tennant法，对流域水资源开发提供借鉴。张小艳等[8]利用多种水文学方法计算了白龙江上游麻牙寺水文站和舟曲水文站断面的生态流量并比较分析了不同方法的经济效益。

沙颍河流域位于河南省中南部，是重要的能源基地，有着豫中南地区的母亲河之称。但沙颍河在枯水期因水动力不足而出现断流现象，因此有必要对其开展生态流量计算保障河流健康。基于水文学生态流量计算方法适用性以及研究发展，决定选用改进年内展布法、Tessman法以及基流比例法在周口断面进行生态流量核算，采用Tennant法[9]对计算得到的结果进行评价分析得出最小生态流量推荐范围。

2 研究区域概况和数据分析

2.1 沙颍河流域概况

沙颍河是淮河左岸的最大一级支流，流域总面积39075.3km2，跨河南与安徽两省，河道全长约621.2km[10]。流域气候表现为四季分明、夏季高温、冬季寒冷、雨热同期，属温带大陆性季风气候，平均年降水量为641.2mm，并有明显的季节性变化，汛期可能发生洪水，枯季可能出现断流现象；且降水量南部较北部大，山区较平原大。

2.2 核算断面的选择

沙河与颍河在周口交汇，在交汇之前沙河与颍河的水质相差较大，在周口断面交汇时流域的分布形状由扇形变为带状，在交汇之后下游水质则主要是受周口断面来水的影响。可见周口断面是沙颍河干流的起始断面，保障其生态流量对维护沙颍河干流的水生态系统至关重要[11]。因此以沙颍河分布形状改变的重要节点——周口断面作为核算断面。

2.3 数据选择

通过收集得到的资料，研究选用沙颍河1988—2017年共30年的实测流量数据进行生态流量核算，求得沙颍河多年逐月平均流量见表1。

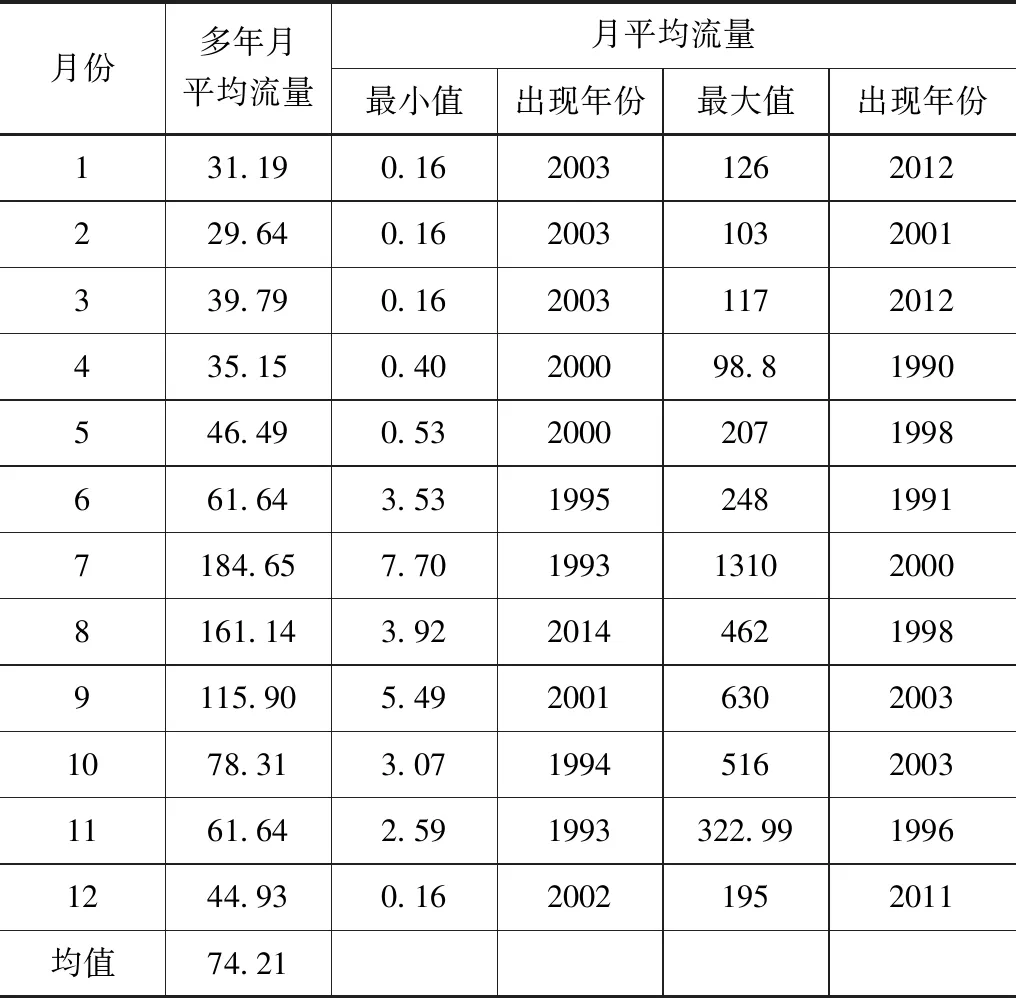
表1 1988—2017年周口断面逐月平均流量 单位：m3/s

由表1可知，沙颍河周口断面降水分布年内明显不均，流量变化较大，呈现出季节差异：最大值可达1310m3/s，而最小值仅为0.16m3/s。

2.4 数据检验

Mann-Kendall法[12]是一种非参数检验方法，因其对样本数据分布没有特别的要求，少数异常值的存在对计算结果基本没有影响，并兼有突变检验功能而被广泛使用。因此针对周口站1988—2017年共30年的年平均流量数据，采用Mann-Kendall法进行趋势检验。计算得到S=-9，Z=-0.14,小于0，说明流量数据整体呈下降趋势。同时结合图1所示的Mann-Kendall突变检验图可知，周口站这30年的年均流量数据没有显著性趋势变化，即流量与年份之间没有一定的相关性[13]。表明流量数据具有一定的科学性、代表性以及可操作性，可以用于沙颍河生态流量计算。

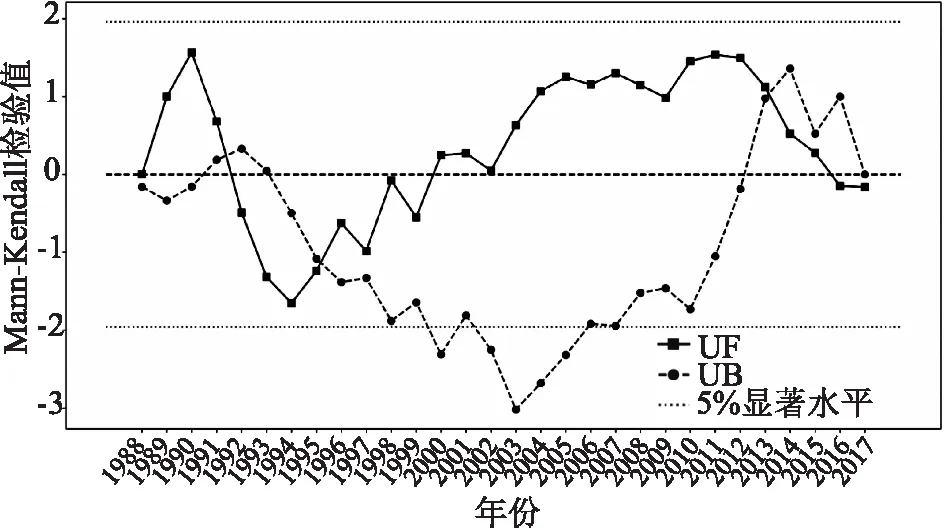
图1 Mann-Kendall突变检验图

3 研究方法与结果

3.1 改进年内展布法

先采用还原方法或模型将实测流量资料还原为天然流量[14]，最终还原结果参见表2。本研究采用逐项还原法[15]。公式如下：

W天然=W实测+W农耗+W工业+W蓄变+
W库蒸发+W引水+W其它

(1)

式中，W天然—天然年径流量，108m3；W实测—实测年径流量，108m3；W农耗—地表水农业灌溉耗损量，108m3；W工业—地表水工业耗损量，108m3；W蓄变—时段始末的水库、闸坝蓄变量，增加为正，减少为负，108m3；W库蒸发—水库、闸坝库区水面蒸发与陆面蒸发差值，108m3；W引水—跨流域引水，108m3；W其它—其他还原水量，108m3。

具体计算过程如下：

(1)依据沙颍河周口站1988—2017年的流量数据资料，将1年划分为丰、平、枯水期。

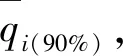
表2 1988—2017年周口断面天然年径流量 单位：108m3

(4)计算不同时期不同的同期均值比η1、η2、η3。

(5)依据公式Qi=ηi×qi，计算各月最小生态流量，计算结果见表3。

3.2 Tessman法

Tessman法[16]是由Tennant法修改而来的，需要划分为丰水期、平水期及枯水期。计算公式如下：

(2)

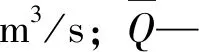
当P<40%时，该月的最小生态流量取为本月平均流量；当40%100%时，该月的最小生态流量为本月平均流量的40%。

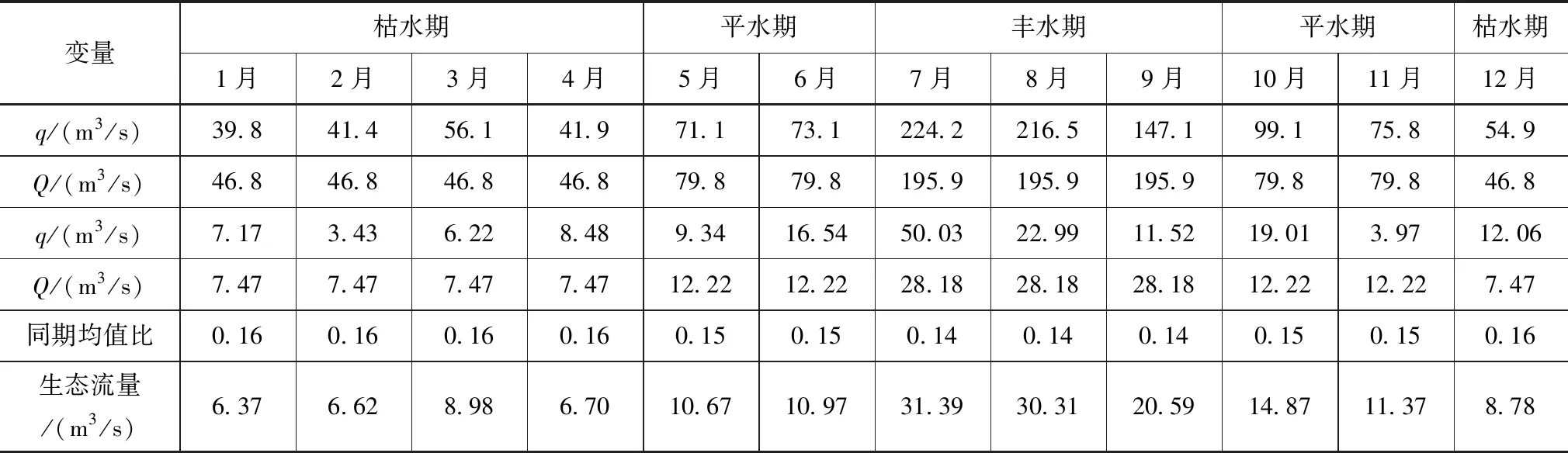
表3 改进年内展布法计算结果

最终计算得到各月P频率及最小生态流量见表4。

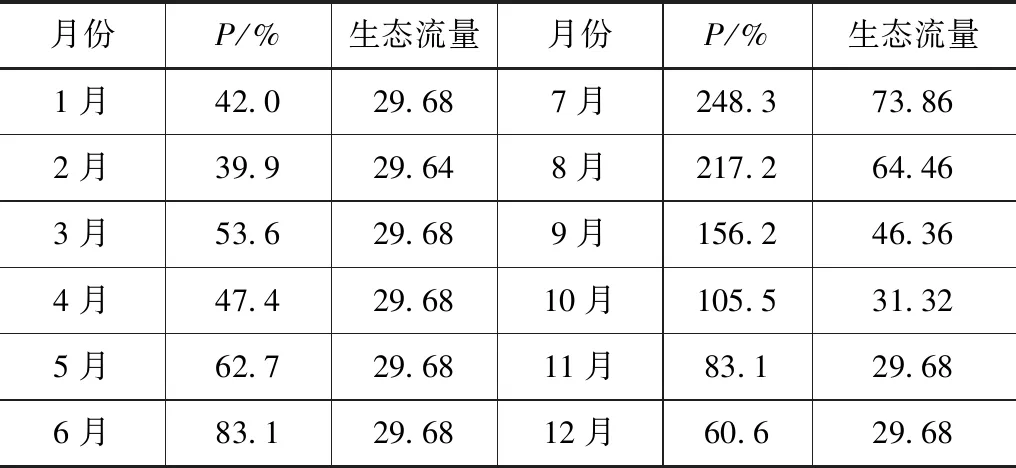
表4 Tessman法各月份频率及最小生态流量表 单位：m3/s

3.3 基流比例法

3.3.1年型划分及其生态流量计算

首先计算距平百分率的大小，再按年份划分标准将1988—2017年分为丰、平、枯及特枯水年等不同年型[17]。不同年型的划分标准见表5。不同年型对应不同基流比例值，但同一年型不同时段采用相同基流比例值。

表5 不同年型划分标准表

生态基流比例计算：

Ta+1=[1+(Qa/Qa+1-1)×μ]×Ta

(3)

设

α=1+(Qa/Qa+1-1)×μ

(4)

则

Ta+1=αTa

(5)

式中，Ta—断面a年型的基流比例，%，a=1(丰水年)、2(平水年)、3(枯水年)、4(特枯水年)；Qa—断面a年型的年均径流量值；μ—比例消减系数，本文中取为0.4。

各年型最小生态流量的计算：

(6)

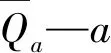
计算所得最小生态流量见表6。

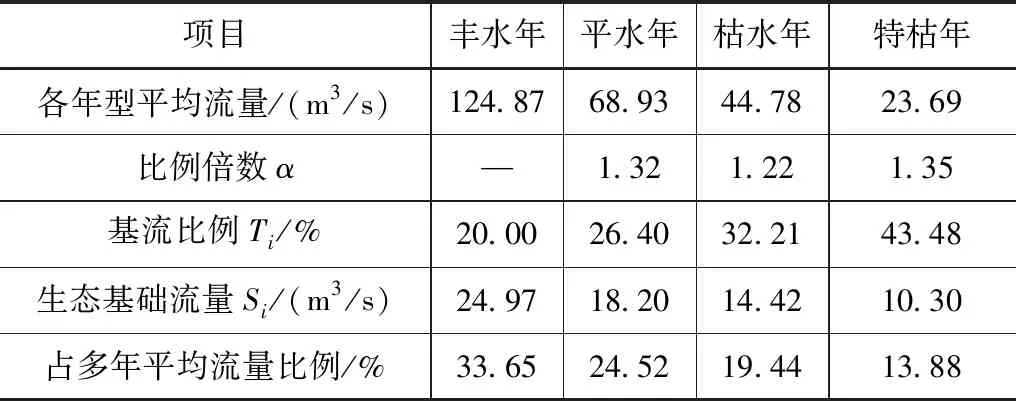
表6 周口站各年型最小生态流量表

从表6中可以看出，丰水年、平水年、枯水年及特枯水年的生态基础流量均达到了多年平均流量的10%以上，可以满足河流最低要求。而丰水年甚至达到了33.65%，可以为大多数水生生物提供较好的生存环境。

3.3.2同一年型内不同时段生态流量的计算

同一年型内根据不同月份的流量大小将其分为丰水期(7—9月)、平水期(10—11、6月)及枯水期(12—5月)等不同时段。3个时段根据同一年型采用同一基流比例分别计算生态流量。

同一年型不同时段最小生态流量的计算：

(7)

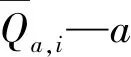
计算结果见表7。

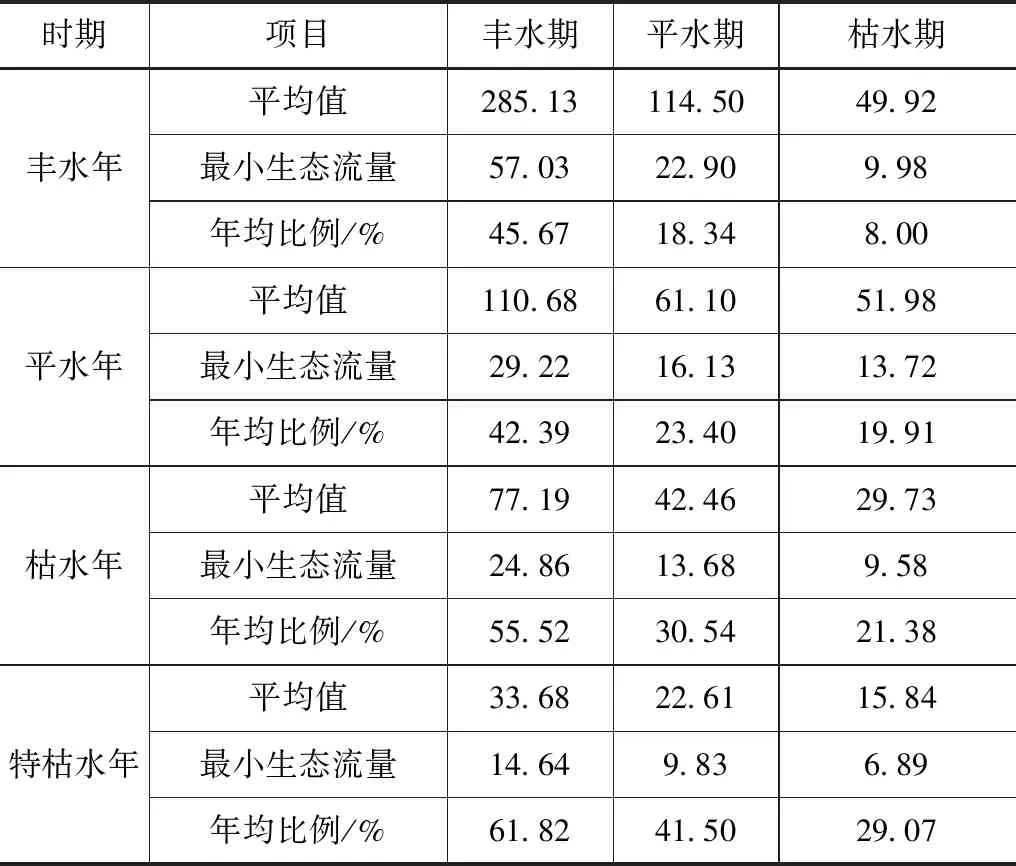
表7 基流比例法生态流量计算表 单位：m3/s

4 计算结果分析与讨论

郭利丹等[18]对Tennant法的应用及合理性进行分析发现：采用同时段的平均流量较多年平均流量进行评价更为合理。因此采用Tennant法对计算结果进行分析评价，其评估参数见表8。以水利部印发的《关于印发第一批重点河湖生态流量保障目标的函》(水资管函〔2020〕43号)[19]中的第一批重点河湖生态流量保障目标(试行)中规定的沙颍河周口断面最小生态流量4.3m3/s为参照值。

P1代表改进年内展布法，P2代表Tessman法，P3—P6分别代表基流比例不同年型比值，以4.3m3/s为参照进行对比表示为P7。各方法所得P值及评估结果见表9。

Tennant法认为多年平均流量的10%是维持河流水生态健康的最低要求，30%能为多数水生生物提供较好的生存环境[20]。而Tessman法的各月流量占多年平均流量比值范围为29.77%～74.57%，比值过大，现实中很难达到；改进年内展布法和基流比例特枯水年的评价结果处于10%～30%之间，较参考值稍好；基流比例法丰、平、枯水年的评价结果高于对比值P7，得到的最小生态流量偏大。

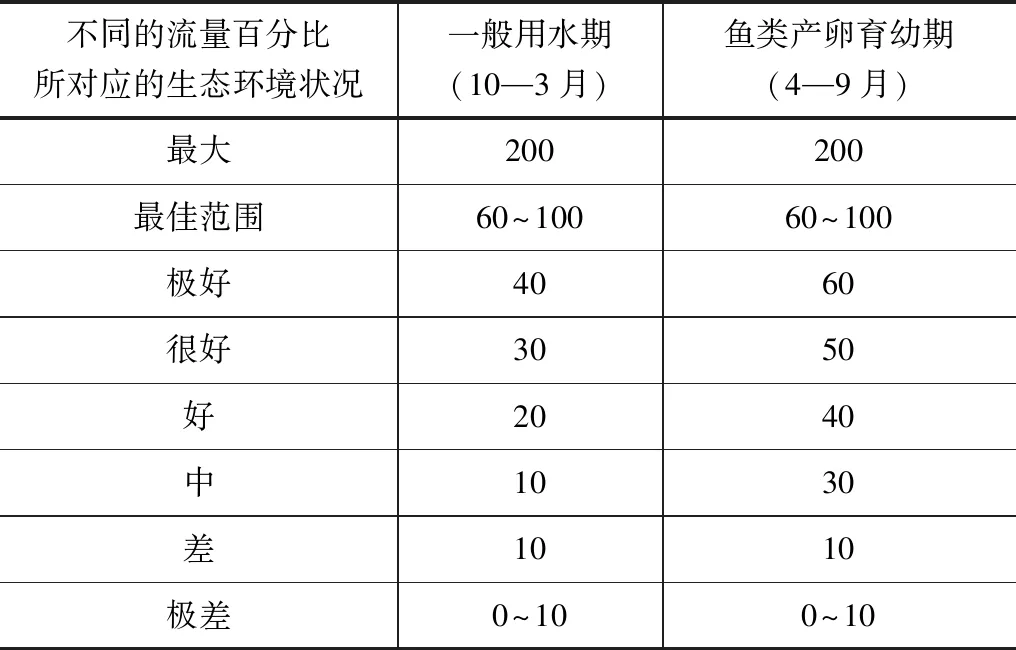
表8 Tennant法评估参数表

结合图2可得，3种方法计算结果均能体现出各月份流量值之间的差异。但Tessman法3月流量值较2月份未体现出上升趋势，与实际不符；基流比例法中7—9月流量是取这3个月多年平均值乘以基流比例得到，与实际情况8月较7月流量值呈下降趋势不符；改进年内展布法各月份流量峰值出现在7月份，符合实际情况。

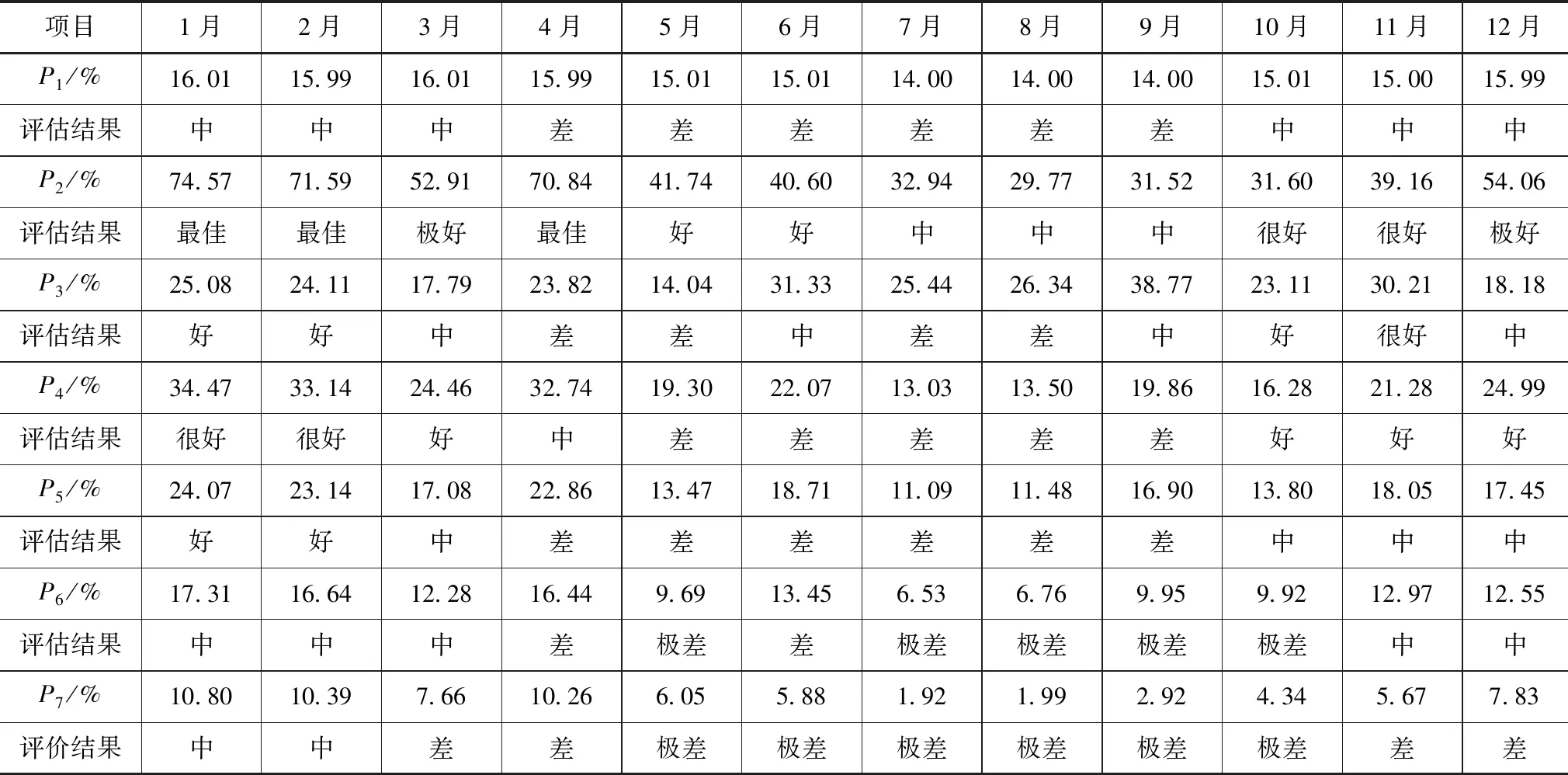
表9 P值及评估结果

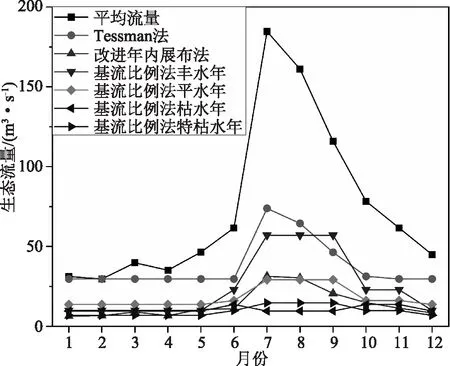
图2 各方法计算结果对比图

5 结论

本文选用了改进年内展布法、Tessman法以及基流比例法3种水文学方法对沙颍河周口断面生态流量进行核算并利用Tennant法对结果进行比较，得到以下结论：

(1)Tessman法计算结果过高，基流比例法丰、平、枯水年计算结果较参照值偏高，基流比例法特枯水年和改进年内展布法的评价结果能更好的贴合参照值。

(2)改进年内展布法计算结果能体现沙颍河实际各月份流量有明显季节性变化的特点，因此选择该法计算沙颍河周口断面生态流量更为合理，得到最小生态流量范围为6.37～31.39m3/s。

研究结果可用于管控沙颍河生态流量，促进流域水生态保护工作，此外，由于生态流量核算工作十分复杂，今后可结合水力学法及生境模拟法进一步完善研究。