LBSO-PID控制方法在工业控制中的应用

彭继慎，李希桐

（辽宁工程技术大学 电气与控制工程学院，葫芦岛 125105）

0 引言

PID控制作为一种算法结构简单且易实现的控制方法已经被广泛应用于各种工业控制系统中[1]。目前，大多数工业控制系统具有大时阶以及非线性的特点，为了提高工业控制效果，需要对影响PID控制效果的比例、积分以及微分三个参数进行整定选择[2]。传统的PID整定方法主要有Z-N法以及工程整定法，但是这两种方法存在受主观影响以及计算量大的问题。随着人工智能算法的不断发展进步，且由于基于人工智能算法的PID整定方法的自适应能力强且整定效果相对传统方法优良，相关研究人员提出利用诸如神经网络、遗传算法等智能算法对PID三个参数进行自整定计算[3～6]，但是这些算法大多存在易陷入局部解，迭代收敛速度慢以及求解精度低的问题。

因而为提高PID参数整定的精度，本文提出一种基于LBSO算法的PID整定方法。该方法结合了BAS算法的局部求解能力、PSO算法的全局搜索能力，从而有效提高了算法对最优解的求解能力，另外，算法结合了Levy随机步长特性，使算法陷入局部解的可能性降低，最后本文通过实验对所提方法进行了验证。

1 PID控制原理

PID控制方法是由比例、积分以及微分环节组成的一种控制方法，其中比例环节主要控制系统的响应速度、积分环节主要为了实现系统的无差调节，而微分环节主要为了减小超调进而改变系统的动态响应性能。其具体控制函数可由式(1)表示：

式中，Kp为比例环节系数、Ki为积分环节系数以及Kd为微分环节系数。由此，其传递函数如式(2)所示：

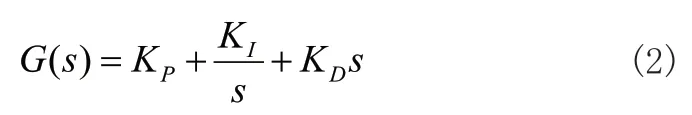
2 LBSO算法建模

有N个个体、D维的Levy-BSO算法其个体可初始化为Xi=(xi1...xii...xiD)，那么其群体即可表示为X=(X1...Xi...XN)，由于算法参考了PSO算法的群体机制，因而对于当前个体最优位置可用Pi=(Pi1...Pii...PiD)表示，那么群体当前最优位置便可表示为Pg=(Pg1...Pgi...PgN)。对个体速度更新计算如式(3)所示[7]：

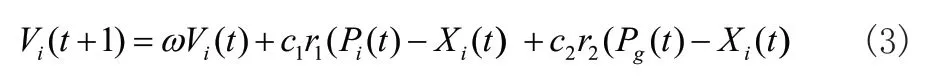
其中ω为算法惯性权重因子，为权衡算法全局与局部搜索能力，该因子更新计算如式(4)所示，另外，c1、c2为算法的两个调节系数，同样为了调节算法的全局与局部搜索范围，具体计算如式(5)所示，而r1与r2为两个0，1之间的随机数。

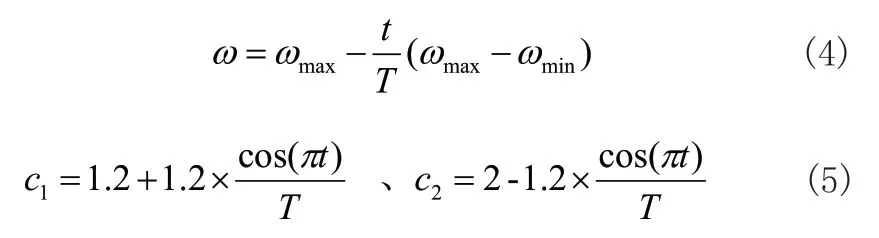
对于算法中个体移动方向与距离，参考了BAS算法的个体特性。对于BAS算法个体左右须位置Xir，Xil计算如式(6)所示：

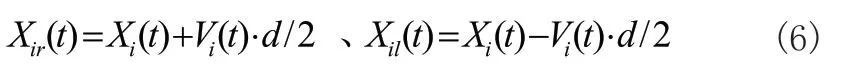
由此算法中个体移动距离与方向更新如式(7)所示：

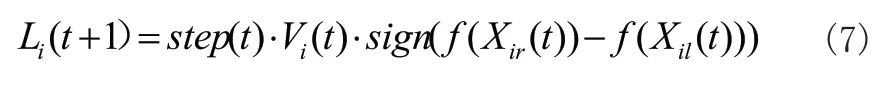
式中，步长step(t)按式(8)进行更新。

式中ept为变步长因子，从而未加入Levy飞行机制的算法个体更新计算如式(9)所示：

式中λ为步长比例因子，本文取0.4。由于Levy的长期短距离飞行、短期长距离飞行机制能够有效提高算法个体的多样性，从而提高算法的搜索范围，进而有效抑制易早熟现象的发生[8]。

对于Levy飞行机制所服从的Levy分布计算式如式(10)所示：

其中，α取值范围为[0,2]，主要用于控制Levy分布图峰的锐度，r为控制分布图跨度的参数取值应大于0。对于α，当其取值为非整数时，难以利用Levy分布的概率密度函数对问题进行分析，一般采用模拟方法来生成Levy分布的随机步长，因而对于加入Levy飞行机制的BSO算法的位置更新式如式(11)所示：

其中α为随机步长，文中经过多次实验，取值为0.45，对于Levy(β)为符合式(12)约束的随机搜索路径。

其中u，v服从标准的正态分布，对于φ计算如式(13)所示：

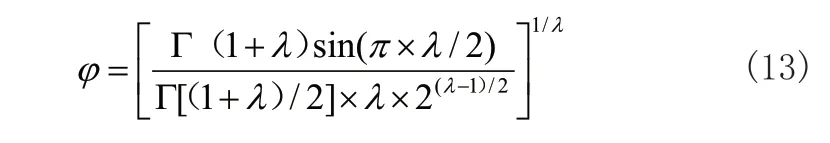
由上可得Levy-BSO算法流程图如图1所示。

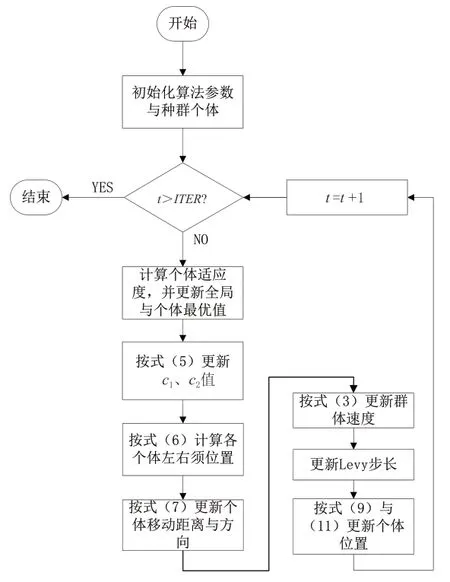
图1 LBSO算法运行流程

3 LBSO-PID控制器的设计

3.1 LBSO-PID控制原理

利用LBSO对PID控制器比例、积分以及微分参数进行优化整定，即通过实现对控制误差的采集与计算来实现对上述三个参数进行优化调节，进而使系统综合性能实现最优，对于LBSO-PID控制器的具体实现框图如图2所示。

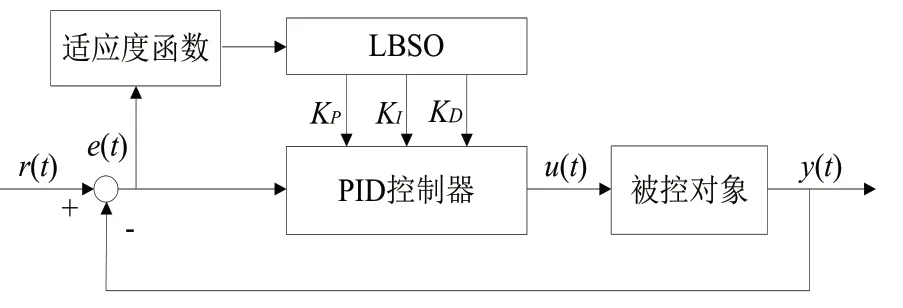
图2 LBSO-PID控制框图

3.2 适应度函数

为了实现对被控对象的良好控制，还须选择一个合适的适应度函数。由于仅考虑输出误差，那么系统的响应速度得不到保障，而若仅考虑响应速度，那么系统的稳定性会很低，因而本文选择了一种基于时间误差绝对值的适应度函数ITAE，其具体计算方式如式(14)所示：

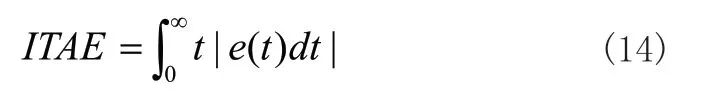
对式(14)进行离散化处理可得到式(15)：

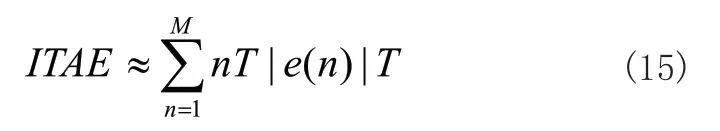
其中，n为采样的次数，M为总的采样次数，T是采样周期。

4 控制效果验证

为了验证所提方法的有效性以及优越性，本文分别利用所提方法以及基于PSO的PID参数自整定方法分别对如式(16)所示的一阶延时系数以及二阶系统进行单位阶跃响应PID控制参数整定。对于PSO以及LBSO参数设置分别如下。设置PSO最大与最小惯性因子分别为0.9与0.2，两个学习因子均为1.2。设置LBSO初始步长为20、须宽为6、变步长因子为0.995，最大与最小惯性因子分别为0.9与0.2，其它参数如前节所述。设置两种算法迭代次数均为150次，种群数均为20。利用上述算法对PID参数进行整定的结果分别如表1与图3、图4所示。

图3 G1系统控制响应结果

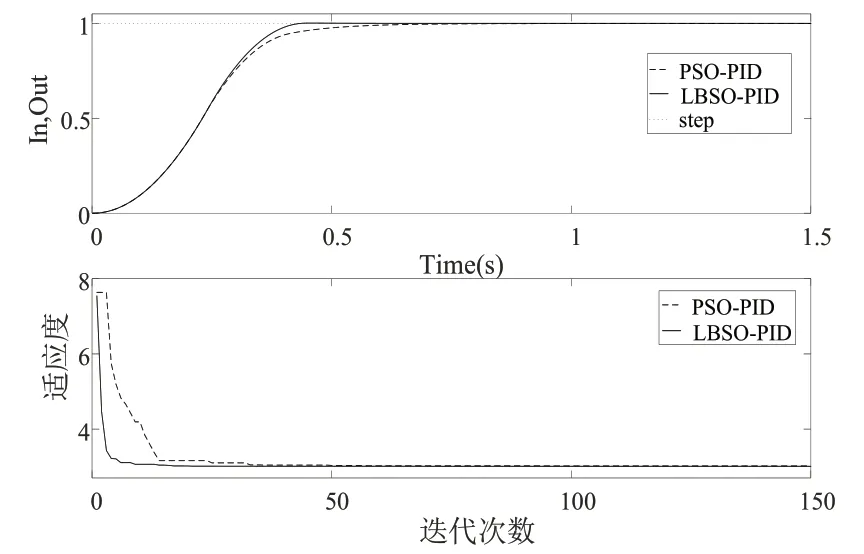
图4 G2系统控制响应结果

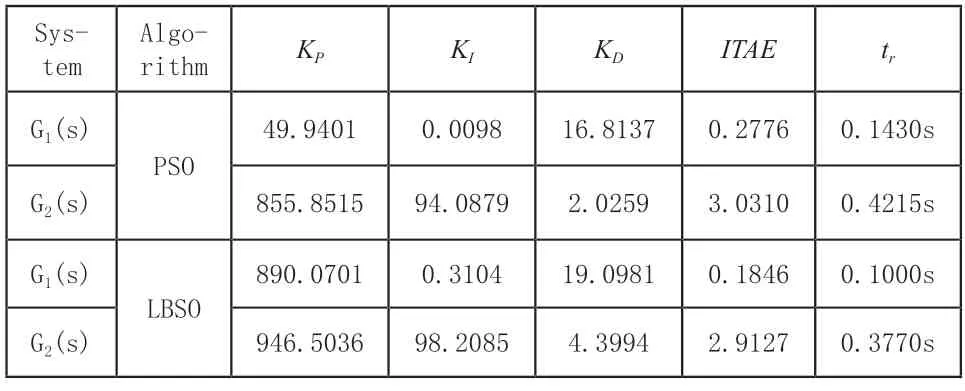
表1 控制计算结果表

由表1给出的计算结果以及图3与图4可以看出，本文所提的LBSO-PID自整定方法在对G1系统的整定，在时间误差绝对值上相对PSO-PID自整定方法相对减少了约33.5%，而在上升时间上相对减少了30%多，而对于G2系统的整定，在时间误差绝对值上相对减少了近4%，在上升时间上相对减少了10.5%多。由此可以看出本文所提方法在控制精度上以及控制速度上相对PSO-PID自整定方法有着很大的优势。另外，由迭代结果可以看出，本文所提LBSOPID自整定方法在迭代速度上相对PSO-PID自整定方法也有着非常明显的优势，由此进一步验证了LBSO算法在PID参数整定计算中的优势。

为了进一步验证所提方法在工业控制中的有效性与普遍适用性，给出所提方法对文献[9]所给出的空压机控制系统PID参数整定结果如图6与表2所示。空压机控制系统传递函数如式(17)所示，给出对于该系统的阶跃响应的结果。

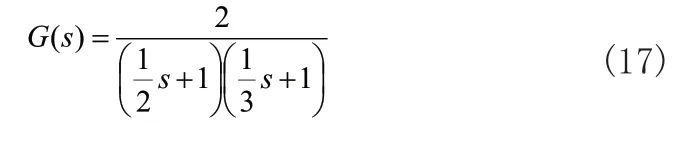
由图5以及表2给出的计算结果再次验证了，本文所提LBSO-PID对空压机系统的控制中，无论在响应速度还是控制精度上均优于PSO-PID方法。另外，由文献[9]所给出的方法的计算结果可以看出，该方法对于空压机控制系统阶跃响应的控制过程中，系统达到稳定所需时间为1s，而本文所提方法仅需0.1211s。

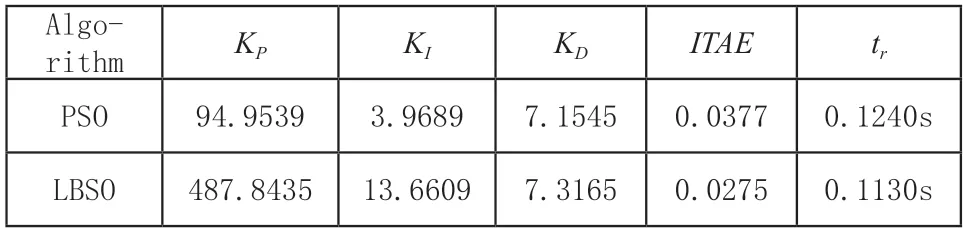
表2 空压机控制系统参数整定结果

图5 空压机控制系统响应结果

5 结语

为了提高PID在工业控制中的效果，本文提出了一种基于LBSO算法的PID参数自整定方法。针对原始BAS算法存在的求解精度低、迭代速度慢以及易早熟的问题，本文引入PSO算法的种群特性以及Levy随机步长特性，有效提高了算法的求解精度以及迭代速度。将LBSO算法应用于PID参数自整定中，利用一阶延时系统、二阶系统以及空压机工业控制实例对其控制有效性以及优越性进行了验证。