基于正交设计试验的永磁同步牵引电机散热的数值模拟研究

武永和， 李祥成， 秦转丽, 杨 成

(1.中车永济电机有限公司，陕西 西安 710016；2.西安中车电气研究院，陕西 西安 710016)

0 引 言

永磁同步电机因功率因数高、效率高、起动转矩大、体积小、质量轻、全封闭、噪声小等优点，广泛应用于机车牵引，但电机散热量也较大[1-2]。电机合理的散热结构能有效将电机各部件温升控制在安全的工作范围内。风冷、液冷和蒸发冷却散热系统是三种常用的电机散热系统[3]。为提高散热效果，电机风冷散热系统的外风路需要在电机机座和端盖上加装散热筋。要研究外风路的散热性能，就要综合考虑散热筋的高度、散热筋的宽度和散热筋的间距对电机散热的影响。正交设计试验法以极差分析模型为基础，是研究多因素、多水平的一种优化设计试验方案[4]，在电机设计和优化方面已有广泛应用[5-10]。为提高试验效率并考虑各因素对试验目标的综合影响，本文结合正交设计试验法和数值模拟分析机座的散热筋参数对电机散热性能的影响，旨在得到最佳散热组合。

1 数值计算模型

1.1 物理模型

本文所涉及的永磁同步牵引电机外风路采用自然散热，具体结构如图1所示。该样机的基本参数如表1所示。

图1 永磁同步牵引电机结构图

表1 电机基本参数

样机机座铸造的散热筋高度H为30 mm，宽度W为6 mm，间距S为20 mm，机座散热筋局部结构如图2所示。

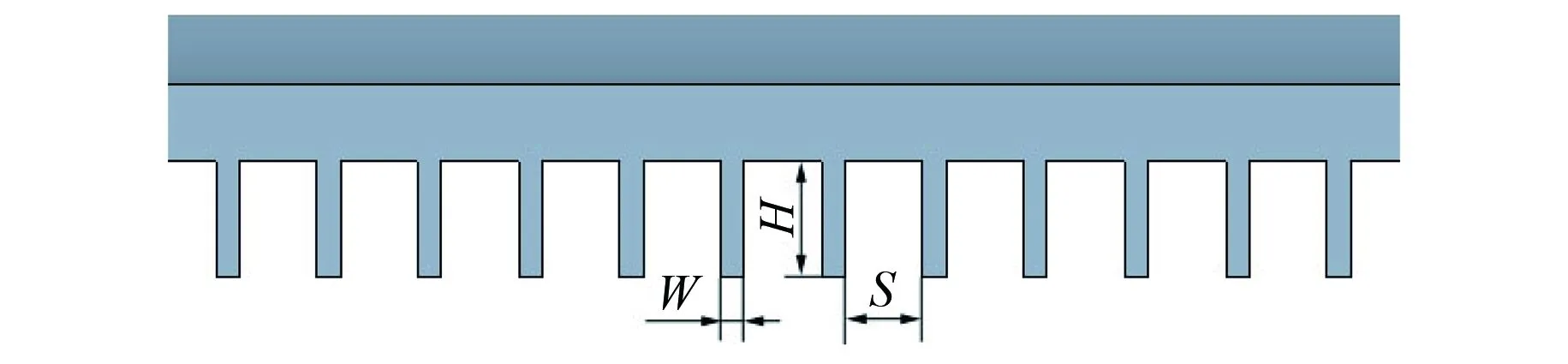
图2 机座散热筋局部结构图

1.2 数学模型

假设电机处于稳定运行状态，近似认为电机内空气物性随其温度线性变化，忽略电机内其他材料的导热系数随温度的变化；假设电机的损耗在同一部件上均匀分布，则计算域的连续性方程为

div(ρU)=0

(1)

式中:ρ为空气密度；U为空气的速度。

动量方程、能量方程可写成如下通用形式[11]：

div(ρVφ)=div(Γgradφ)+S

(2)

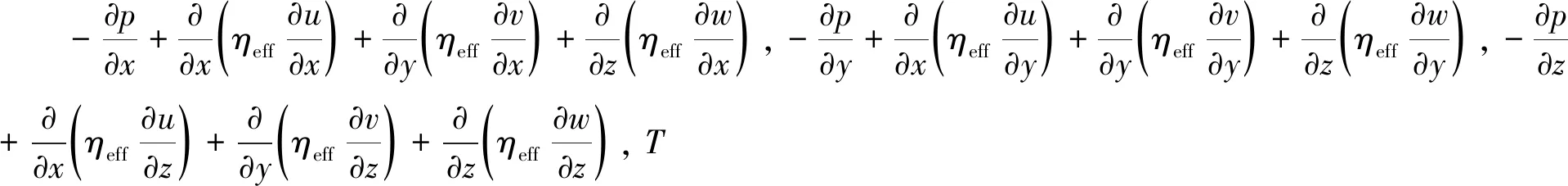
1.3 边界条件

为提高计算效率，同时满足工程实际需要，将定子绕组、绝缘等复杂结构等效为一个均匀的发热体[12-13]。经计算，额定工况下永磁同步牵引电机的损耗如表2所示。

表2 电机各部件损耗 kW

两侧轴承冷却风扇的进、出口边界条件均为压力边界条件。

旋转流体域和静止流体域交界面采用interior边界[11]。

流体和固体交界面速度采用无滑移固壁边界条件，即uair=uwall。

流固界面和固固界面热边界采用耦合边界条件[14]。

机座和端盖向周围空间自然散热，表面传热系数按下式计算[15]：

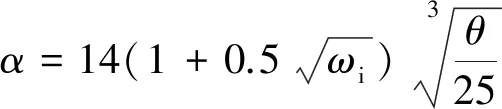
(3)

式中：α为表面传热系数；ωi为吹拂机座内壁的风速；θ为机座壁外表面的温度。

2 正交设计试验

2.1 试验指标和因素

本文选取定子绕组最大温度作为衡量机座散热能力的试验指标。散热筋的高度、宽度、间距为本文的研究变量，即确定正交表为3因素。

2.2 正交表和水平选择

各因素水平数的确定应满足实际情况和正交试验的原则，标准表的水平数均相等且只能取素数或素数幂[6]，本文选取3水平，各因素水平表如表3所示。

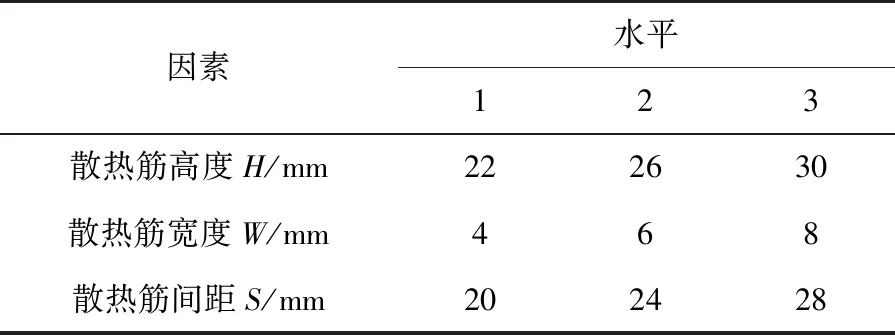
表3 各因素水平表

本文试验研究为3 因素3水平，进行全面组合方案需进行27次试验，若采用正交表L9(34)进行试验，只需做9次。正交设计试验方案见表4。

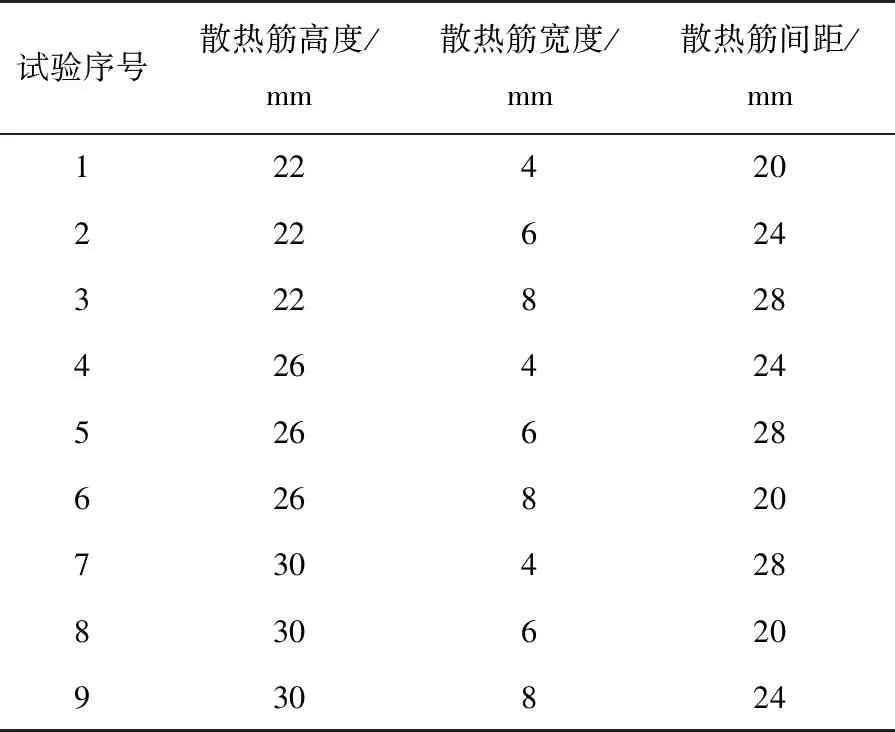
表4 正交设计试验方案

2.3 结果分析

根据正交设计试验方案，采用ANSYS Fluent软件对电机流场、温度场进行耦合计算，得到的仿真计算结果如表5所示。A代表散热筋高度，B代表散热筋宽度，C代表散热筋间距。

2.3.1 直观分析

根据正交设计试验方案和仿真计算结果可以直观看出，所有试验中，试验8的定子绕组最大温度的值最小，说明该方案下电机的散热能力最好，所以最佳的水平组合为A3B2C1。

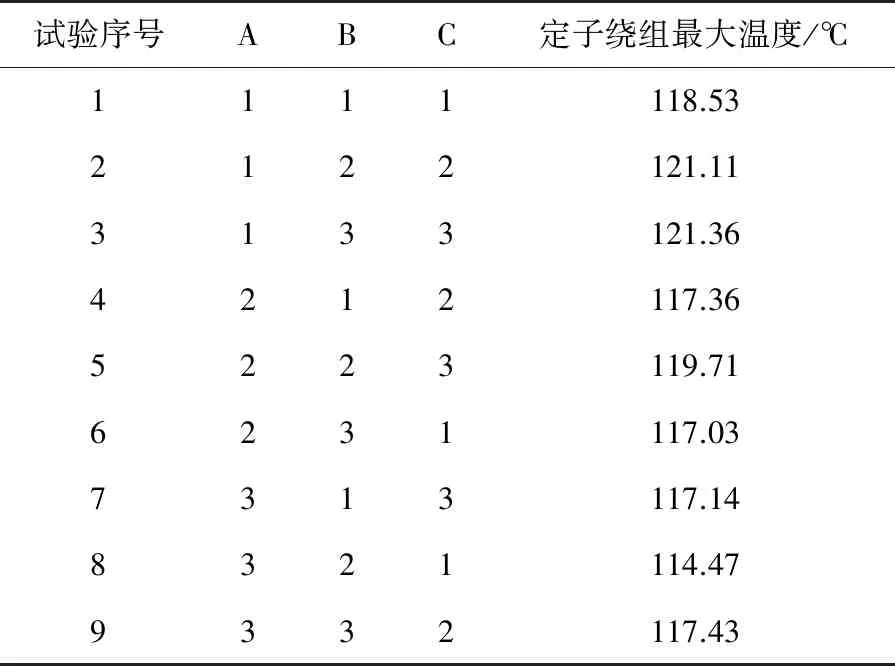
表5 正交设计试验方案和仿真计算结果

2.3.2 极差分析

根据计算结果，对试验指标进行极差分析，结果如表6所示。从表6可以看出，3个因素中，散热筋宽度的极差最小，对定子绕组最高温度影响最小，散热筋高度的极差最大，对定子绕组最高温度影响最明显。根据极差R值的大小，影响定子绕组最高温度的各因素主次顺序依次为散热筋高度、散热筋间距、散热筋宽度。

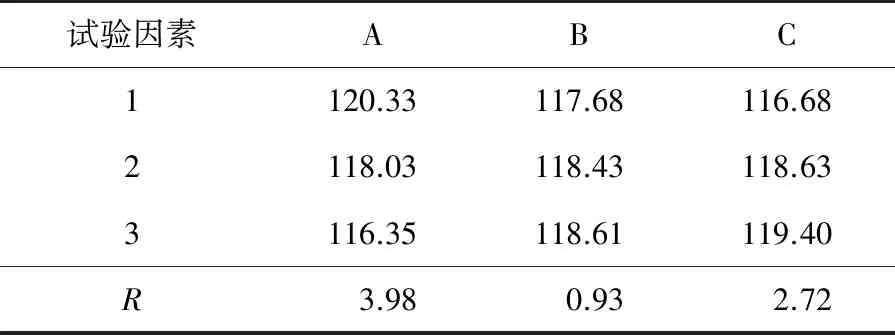
表6 定子绕组最高温度极差分析

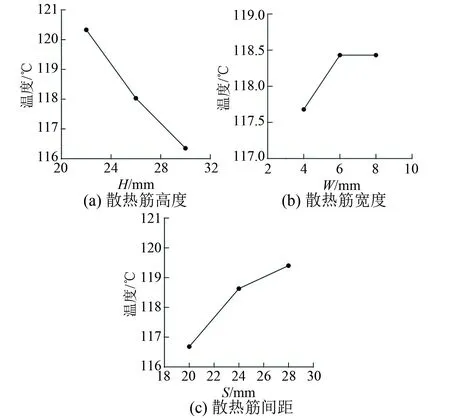
图3 各因素水平对指标的影响分布图

各因素水平对指标的影响如图3所示。从图3中可以看出，定子绕组最大温度随着散热筋高度的增加而降低，这是因为散热筋高度增加后机座表面有效散热面积增加，电机散热能力提高；定子绕组最大温度随着散热筋宽度的增加先升高后基本保持水平，说明散热筋宽度的逐步增加并不能有效提高电机的散热能力；定子绕组最大温度随着散热筋间距增加而升高，这是因为散热筋间距增大，机座表面有效散热面积减小，电机散热能力降低。通过各因素水平对指标的影响分布图可以确定最佳的组合为A3B1C1。

综上所述，散热筋的高度取30 mm，散热筋的间距取20 mm，考虑到材料成本和电机减重要求，取散热筋的宽度为4 mm。所以最佳的水平组合为A3B1C1。

3 试验验证

分别采用电阻法和预埋温度传感器的方法对样机额定状态下稳态运行时的定子绕组平均温升和定子铁心温度进行测量，测试方法和过程均参照相关标准[16]。图4为定子铁心周向埋置温度传感器的位置，温度传感器的轴向位置在定子铁心正中心。

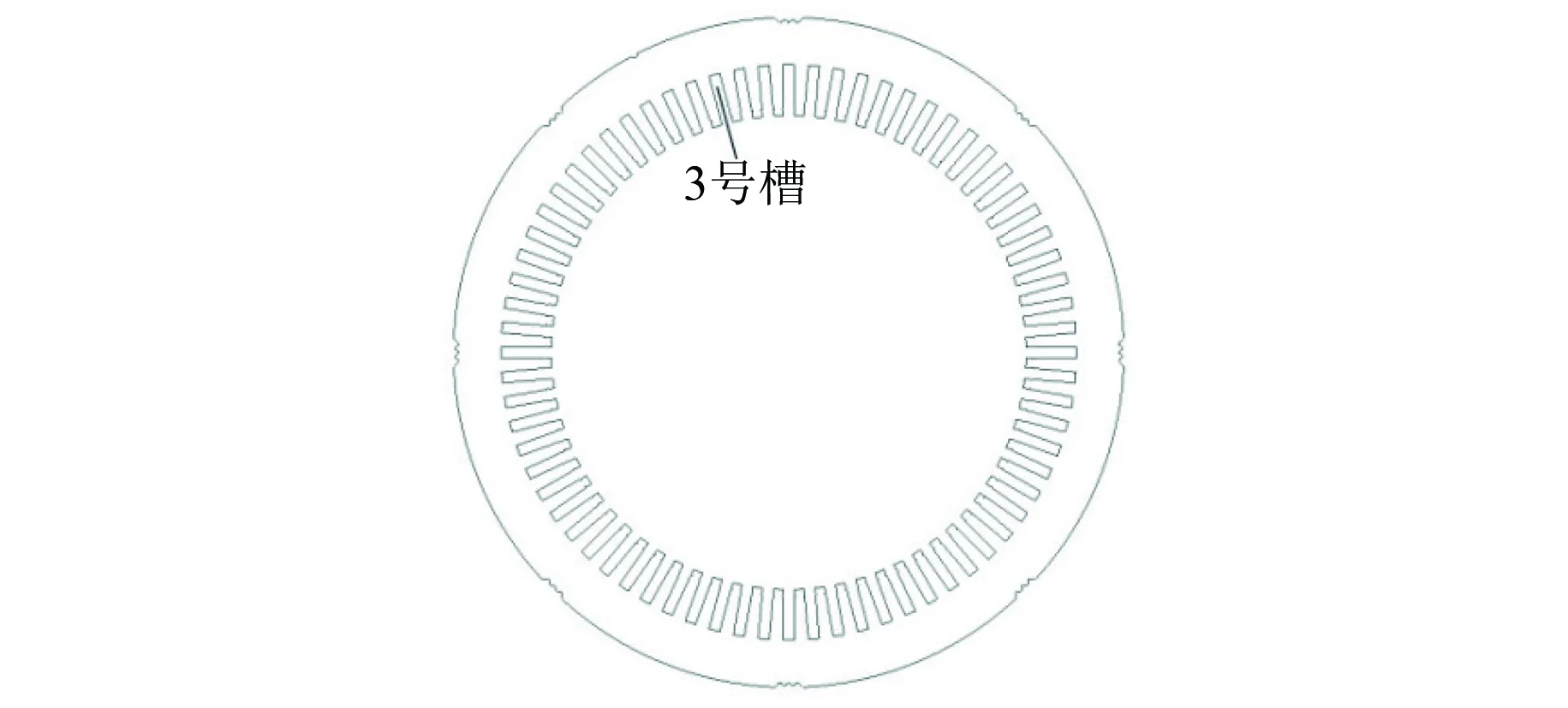
图4 定子铁心测温点周向埋置位置

样机温升试验系统如图5所示。试验的相关参数如表7所示。试验过程中样机保持在额定工况下运行，温升持续时间为420 min。

图5 电机温升试验系统

表7 试验相关参数

定子绕组平均温升和定子铁心测温点温度的数值计算结果与试验结果对比如表8所示，对比结果表明，仿真的最大相对误差小于8%，满足工程要求，验证了本文数值计算方法的可靠性。

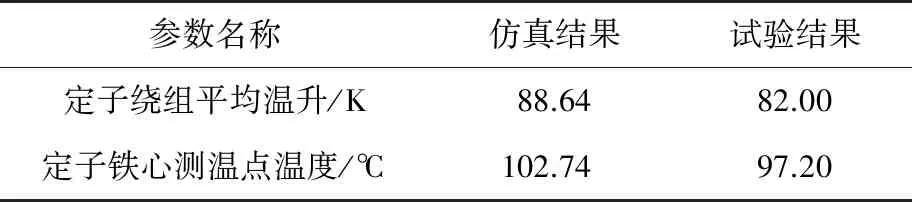
表8 数值计算结果与试验结果对比

4 数值计算结果分析

图6为电机轴向截面温度分布云图，从图6中可以看出，定子线圈端部和定子铁心齿部位置的温度明显高于其他位置，这是因为电机转速慢，电机内部空气流动速度小，定子绕组端部和定子铁心齿部槽口位置换热慢。两端轴承位置分别装有冷却风扇，风扇周围的空气域温度低于附近的固体温度。

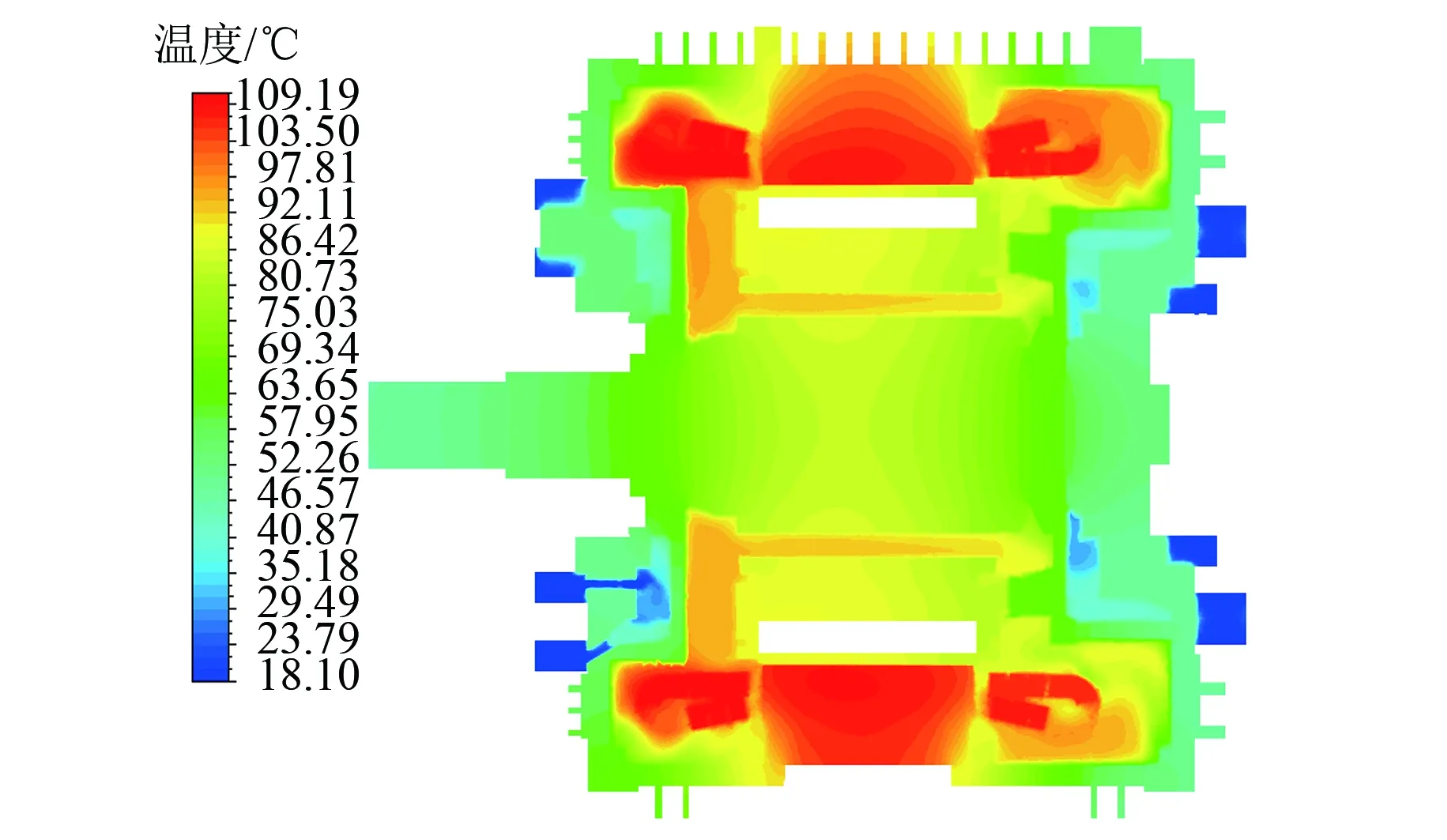
图6 电机轴向截面温度分布云图

图7为电机径向截面温度分布云图，从图7中可以看出，转子组件整体温度低于定子组件，这是因为转子组件损耗小于定子组件；有散热筋的定子铁心位置温度明显低于无散热筋的位置，这是因为散热筋增加了散热面积，有效增强了散热。

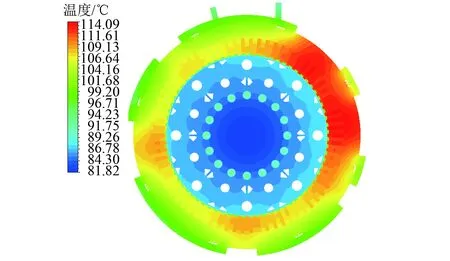
图7 电机径向截面温度分布云图

为研究定子铁心不同位置的温度分布，在定子铁心四个位置分别取线l1、l2、l3、l4，取样线在定子铁心上的位置如图8所示。

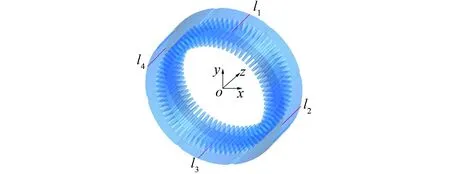
图8 取样线在定子铁心上的位置

图9为不同试验模型的l1沿轴向的温度分布。从图9中可以看出，不同计算模型的l1沿轴向的温度分布趋势相同，均呈抛物线分布。在同一位置，试验8的l1沿轴向的温度最低，试验3的l1沿轴向的温度最高。所有模型的非传动端温度略低于传动端，这是因为非传动端侧的绕组端部空间较大，转子转动时带动空气流动，非传动端侧的换热能力更好。

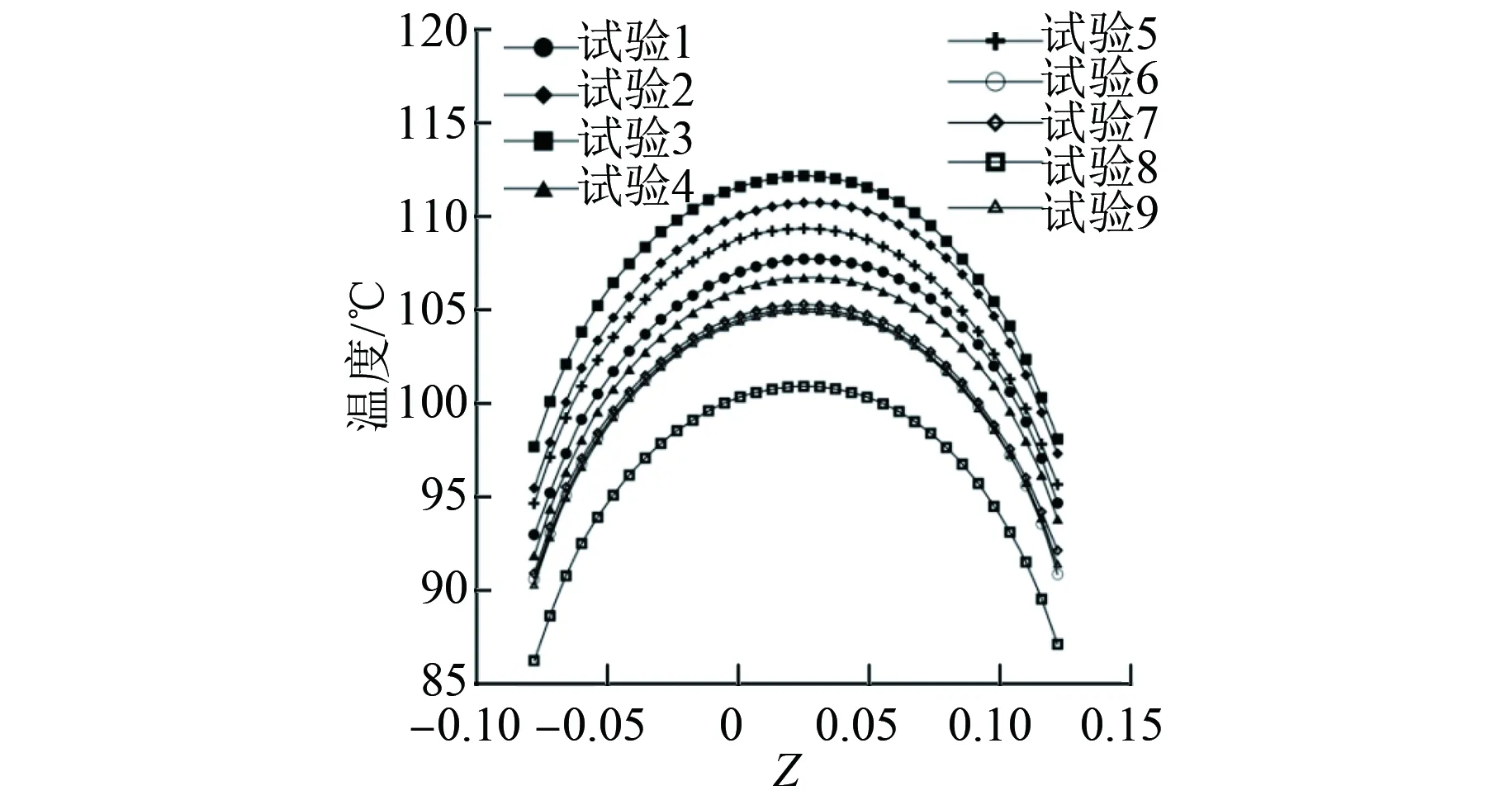
图9 l1沿轴向的温度分布

图10为不同试验模型的l2沿轴向的温度分布，从图10中可以看出，不同模型的l2沿轴向的温度分布趋势相同，均呈“几字形”分布，沿轴向在-0.058 m和0.102 m范围内，温度变化较小，这是因为定子铁心在这个区间局部裸露在空气中，定子铁心表面直接与空气进行对流换热，换热量恒定。在同一位置，试验8的l2沿轴向的温度最低，试验3的l2沿轴向的温度最高。

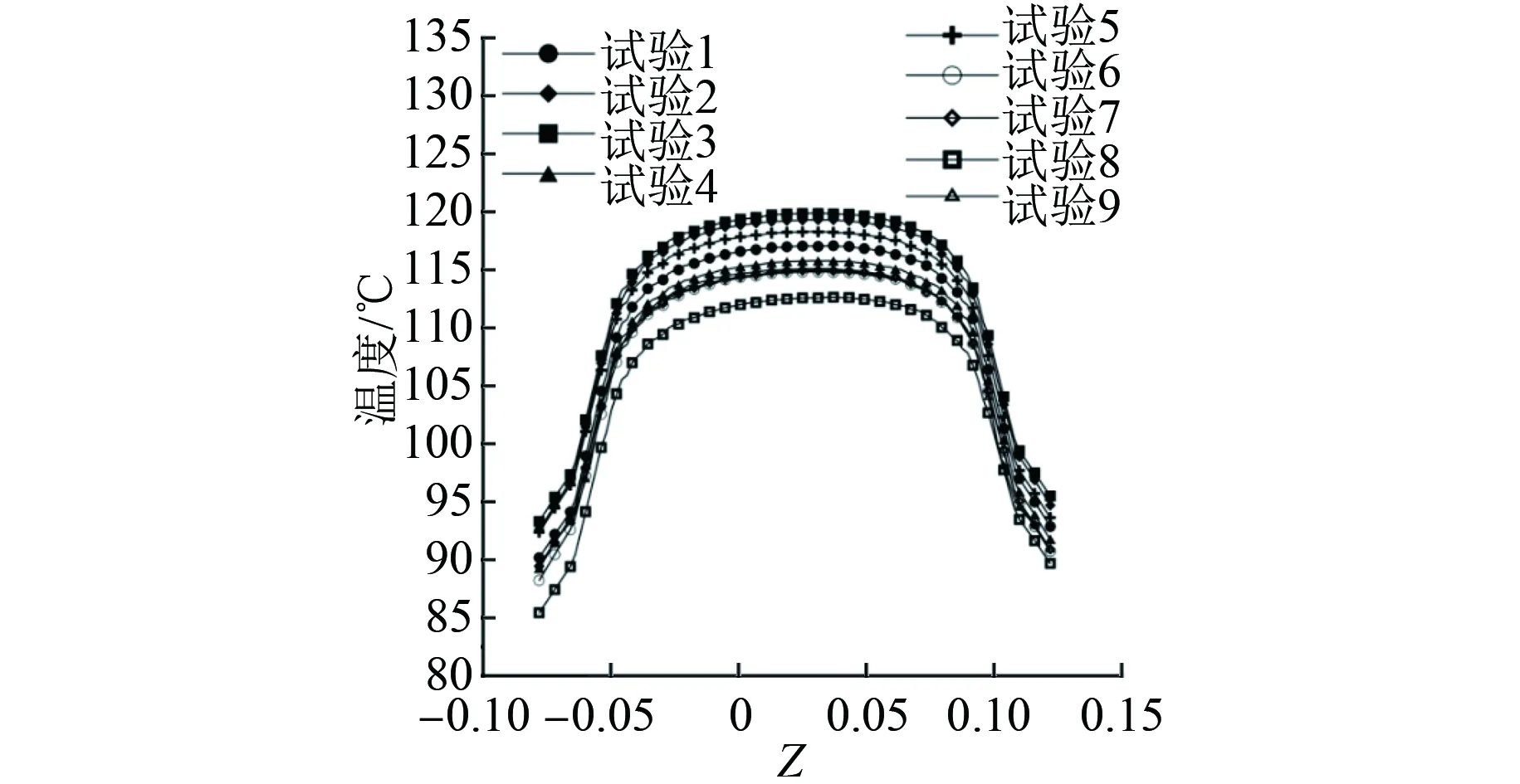
图10 l2沿轴向的温度分布

图11为不同试验模型的l3沿轴向的温度分布，从图11中可以看出，不同模型的l3沿轴向的温度分布趋势相同，均呈“几字形”分布，在同一位置，试验8的l3沿轴向的温度最低，试验3的l3沿轴向的温度最高。在-0.058 m和0.102 m位置温度变化比较剧烈，是因为这两个位置是机座和裸露空气的交界处，定子铁心散热方式由导热转为对流换热。

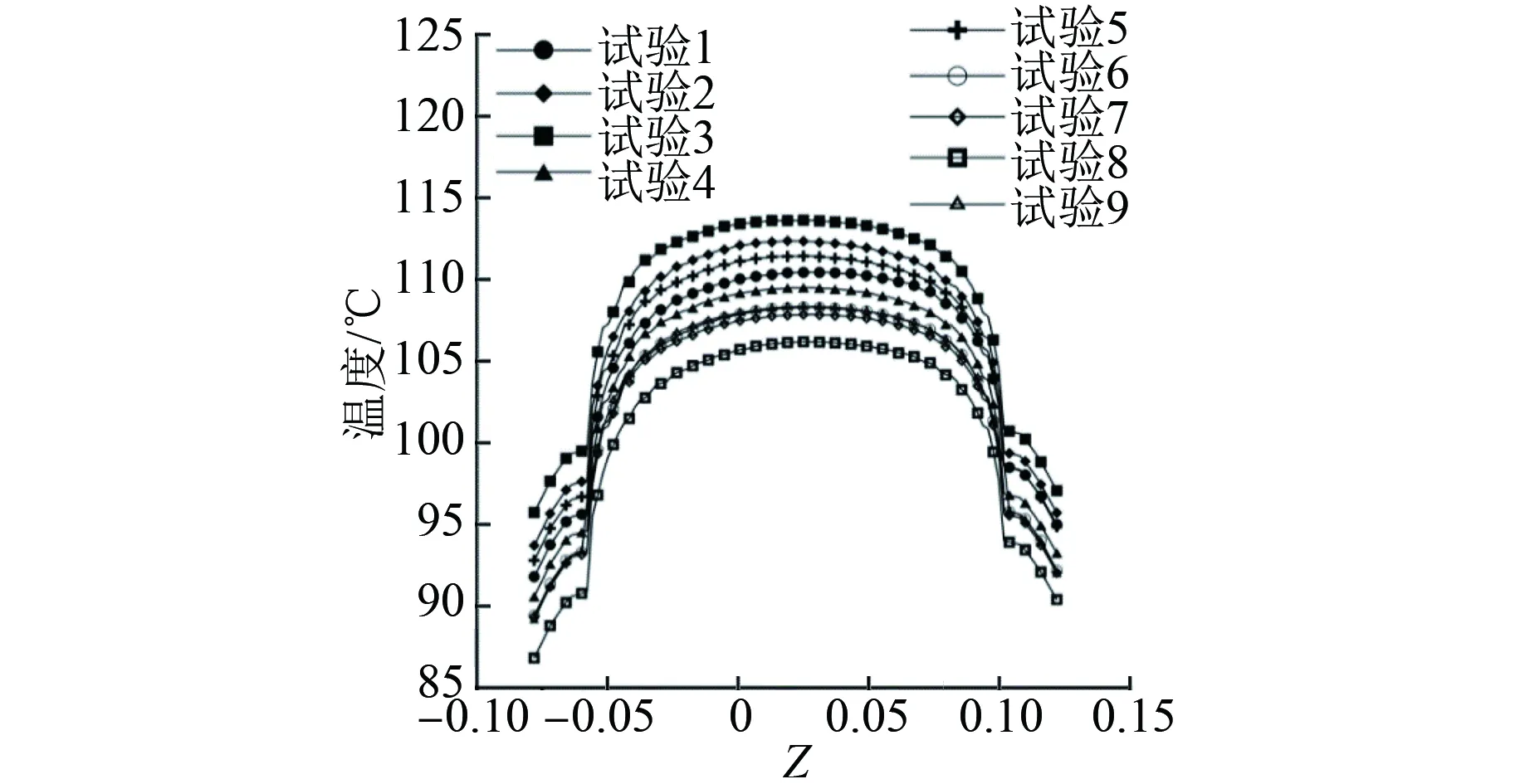
图11 l3沿轴向的温度分布

图12为不同试验模型的l4沿轴向的温度分布，从图12中可以看出，不同模型的l4沿轴向的温度分布趋势相同，均呈“几字形”分布，在同一位置，试验8的l4沿轴向的温度最低，试验3的l4沿轴向的温度最高。所有模型的非传动端温度略低于传动端。

5 结 语

本文以定子绕组最高温度为试验指标，结合正交设计试验法和数值模拟方法分析机座的散热筋参数对电机散热性能的影响进行了研究，发现影响定子绕组最高温度的各因素主次顺序依次为散热筋高度、散热筋间距、散热筋宽度。与试验结果进行了对比验证，最大相对误差小于8%，满足工程要求。从计算结果可知，定子线圈端部和定子铁心齿部位置的温度较高，转子组件整体温度低于定子组件。不同计算模型的l1沿轴向的温度均呈抛物线分布，l2～l4沿轴向的温度均呈“几字形”分布。