基于粒子群优化算法的TMPS-HESM联合仿真设计方法

庞 亮， 张闻东， 胡豁达， 赵朝会

(上海电机学院 电气学院，上海 201306)

0 引 言

近年来，为了保障能源和环境安全，我国提出一系列促进能源结构升级的政策，在工业领域大力发展以体积小、质量轻、高功率密度、高转矩密度为优点的永磁电机[1-2]。然而永磁电机仅有单一励磁源，导致其气隙磁场调节困难，很大程度限制了电机弱磁调节下的升速能力和增磁调节下的增矩能力，以及发电运行时的稳定调压能力[3]，为实现永磁电机气隙磁场可调节性，混合励磁同步电机(HESM)逐渐成为了研究热点，并在新能源汽车、船舰推进、航空航天等领域具有非常广泛的应用前景[4]。

文献[5-6]设计了一种磁分路式径向结构HESM，论述了该电机的结构和工作原理，分析了磁分流点和磁不分流点对应的气隙磁密大小，并研究了转子磁分路式HESM的空载特性，分别讨论了永磁部分和电励磁部分长度对电机空载特性的影响，通过仿真和试验表明，此类电机比较适合短粗结构。文献[7-8]提出了一种切向/径向并联磁路混合励磁发电机，对其磁场分布、静态特性和运行特性进行分析，结果表明该电机具有良好的调磁能力，但其气隙磁密谐波含量较高，影响了电机运行的稳定性。文献[9]讨论了混合励磁开关磁链电机转子极数对电机调磁性能的影响，分析了不同定转子极数电机的拓扑结构和工作原理，运用有限元计算法比较了不同励磁电流密度对电机电磁性能的影响。文献[10]提出了一种双交错HESM，分析了电机等效磁路，通过建立等效磁路模型计算出电机磁路磁阻，求出了电枢绕组中的感应磁通。通过有限元仿真法得到了电机不同励磁电流条件下的电磁特性，验证了提出等效磁路模型的有效性。

综上所述，学者们对磁分路式径向结构、开关磁链结构和双交错结构等HESM研究较多，对于切向聚磁型并联结构混合励磁同步电机(TMPS-HESM)研究较少。TMPS-HESM对比传统HESM，其附加磁路少、气隙磁场调节范围广、容错能力好[11-12]，同时由于永磁磁路结构和电励磁磁路结构并联，TMPS-HESM的电励磁磁路不通过永磁体，电机励磁效率较高，以及不易发生永磁体退磁风险。

本文基于磁路法确定电机主要尺寸，借助ANSYS RMxprt软件设计电机定子，再通过Maxwell & Workbench & Optislong联合仿真软件建立8极48槽TMPS-HESM模型，运用粒子群优化(PSO)算法进行全局多目标优化得到Pareto最优解集，使用优劣解距离法(TOPSIS)从Pareto解集中客观选取最优设计方案，并通过相关有限元仿真试验验证了电机性能符合设计要求。

1 TMPS-HESM的拓扑结构

本文所设计的TMPS-HESM如图1所示。

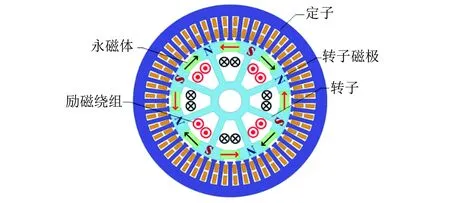
图1 TMPS-HESM结构示意图

该电机的励磁绕组以集中式绕组方式绕在转子齿部，产生电励磁磁动势。在相邻转子极靴侧面的2个平行面形成矩形槽口，用于安装产生永磁磁动势的切向充磁永磁体。电机内部的气隙磁场可以通过改变励磁电流的大小进行调节，从而实现增磁、弱磁等多种工作状态。

在不考虑电机漏磁和磁饱和现象情况下，建立电机在不同励磁电流条件下等效磁路模型，分析电机调磁原理，为下文电机电磁设计和相关性能研究提供理论基础。

电机等效磁路模型如图2所示，其中，FPM为永磁磁势；ΦPM为永磁磁通；RPM为永磁磁阻；Rs为定子磁阻；Rr为转子磁阻；Rδ为气隙磁阻；Φδ为气隙磁通；Ff为电励磁磁动势；Φf为电励磁磁通；Φr为转子铁心磁通；Rrb为转子靴部磁阻；Rry为转子轭部磁阻；Rrt为转子齿部磁阻；Rrta为转子上齿部磁阻。当励磁绕组不通电，即励磁电流为0 A时，由于转子铁心磁阻远小于气隙磁阻，永磁磁通大部分在转子内形成磁短路，仅有少部分磁通通过电机气隙，提供少量气隙磁场。励磁绕组通入负方向电流时，励磁磁通同样在转子内形成磁短路，不通过电机气隙的励磁磁动势可忽略不计，此时的磁路等效模型与励磁绕组为0 A时近似。图2(a)的等效磁路方程如下所示：

Φδ=ΦPM-Φr

(1)

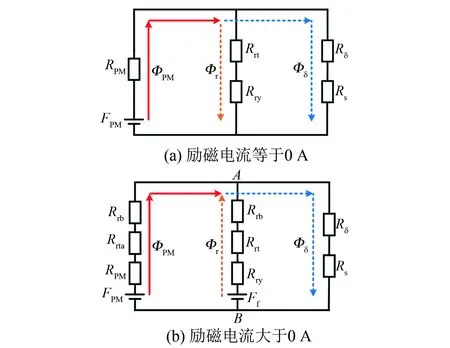
图2 TMPS-HESM等效磁路模型

由式(1)可知，电机气隙磁通Φδ较小，因为永磁磁动势仅有少部分通过电机气隙，大部分由于转子磁短路现象通过转子铁心，产生较大转子磁通Φr。当励磁电流为负方向时，电励磁磁通流经转子铁心，增大电机转子磁通，进一步削弱电机气隙磁通，增加电机弱磁升速能力。

如图2(b)所示，当励磁绕组通入正向电流，励磁电流大于0 A时，电励磁磁通Φf和永磁磁通ΦPM共同构成电机的气隙磁通Φδ。永磁磁通通过转子上齿部Rrta和转子靴部Rrb进入电机气隙，流经电机定子形成闭合回路。电励磁磁通通过整个转子进入电机气隙，流经定子形成闭合回路。设A与B之间的磁动势差为F1，永磁磁阻和转子部分磁阻组合为Rz，则图2(b)等效磁路方程如下：

(2)

式中：Rrb+Rrta+RPM=Rz；Rrt+Rry+Rrb=Rr。

电机气隙磁通可表现为

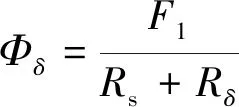
(3)

由式(3)可知，气隙磁通Φδ受磁动势差F1的影响。而式(2)表明了F1的大小由永磁磁动势FPM和电励磁磁动势Ff决定。由于电机的永磁磁动势FPM远大于电励磁磁动势Ff，永磁体磁阻RPM远大于转子磁阻Rr，并且在图2(b)等效磁路模型中，永磁磁动势和电励磁磁动势互为并联，因此电励磁磁动势Ff决定了磁动势差F1的大小。同时，根据等效磁路模型，F1的变化会导致永磁磁动势FPM随之改变，因此推导出FPM受控于Ff。

TMPS-HESM具有较好的调磁能力。随着励磁电流增大，导致电励磁磁动势增大，从而影响永磁体工作曲线，增大永磁磁动势，使得电机气隙磁密和磁场强度增大，提升电机增磁增矩能力。 当励磁电流减小，电励磁磁通流经转子铁心，增大电机转子磁通，进一步削弱电机气隙磁通，增加电机弱磁升速能力。

2 TMPS-HESM设计方法

该TMPS-HESM由于其特殊结构，无法用ANSYS RMxprt、Motor-CAD等现有电机磁路设计软件进行直接设计，故如何利用现有软件进行TMPS-HESM的设计是值得研究的，以表1电机参数为例，进行TMPS-HESM设计方法讨论。

表1 TMPS-HESM主要参数设计范围

2.1 基于RMxprt设计TMPS-HESM定子

根据功率和转速等额定点数据来确定电机定子铁心内径D和定子铁心有效长度lef这2个电机主要尺寸，并由此来确定电机的其他尺寸[13-14]。电机体积和主要尺寸的基本关系式如下所示：

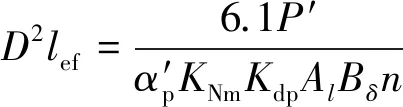
(4)

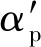
根据式(4)可以计算出电机主要尺寸D2lef=3.1×10-4m3，相同D2lef的电机可以设计得细长，也可以设计成短粗型，为反映电机这种几何形状的关系，引入电机主要尺寸比λ如下：

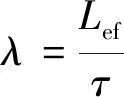
(5)

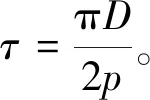
本文所设计TMPS-HESM由于转子上同时存在永磁磁动势源和电励磁磁动势源，为了放置电励磁绕组需要对转子开槽处理。因此，需要转子外径稍微大一些，电机呈现短粗型，从而选取λ=1.06。根据式(5)可得电机电枢直径D为96 mm，电枢轴向长度lef为40 mm。

在确定电机额定数据、电磁负荷、电机尺寸的条件下用RMxprt软件设计了一个与本文所设计TMPS-HESM相同尺寸、相同定子结构、相同定子绕组、相同极槽配合的8极48槽永磁电机模型如图3所示。

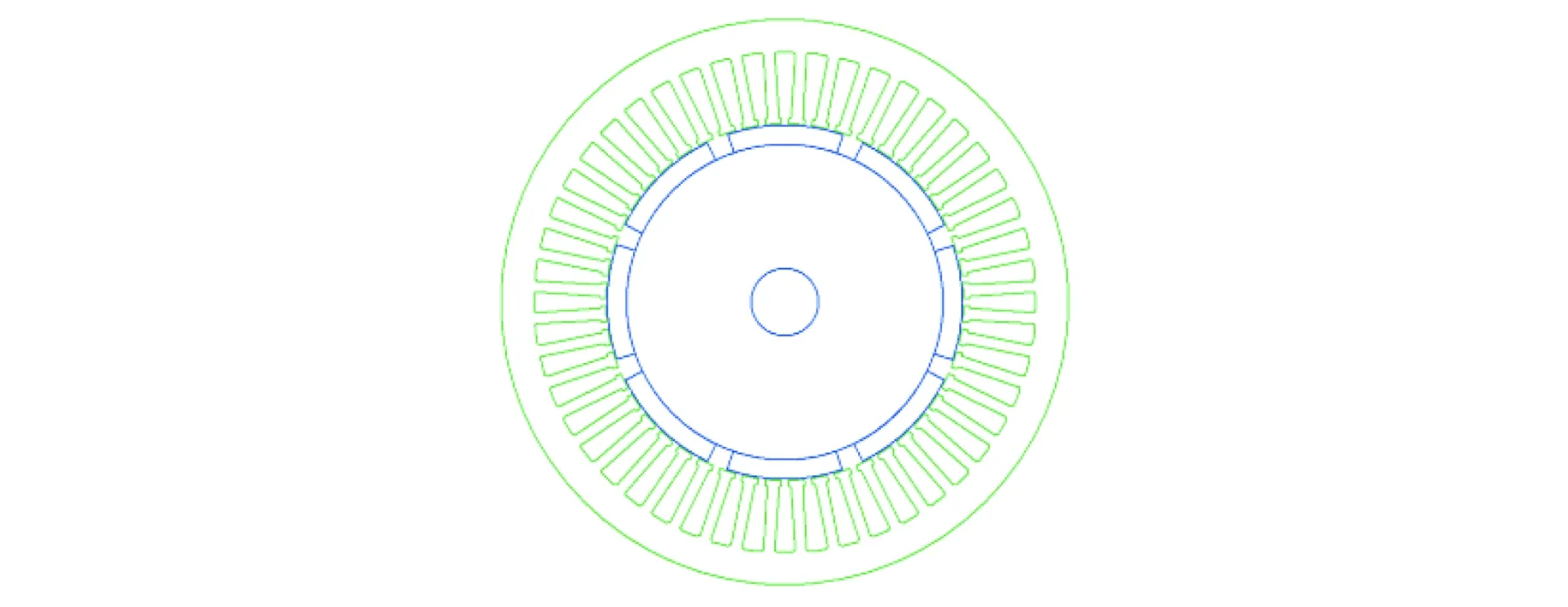
图3 永磁电机模型

通过RMxprt进行磁路计算，该永磁电机的定子齿部和轭部最大磁密为2.0 T，符合定子铁心软磁材料DW310_35的B-H曲线磁饱和规律；该永磁电机的电负荷和磁负荷分别为26 858.2 A/m和0.801 T，符合TMPS-HESM电磁负荷分别为26 000 A/m和0.8 T的要求。图4所示，该电机定子绕组相数为3，绕组层数为2，平均节距为5，符合本文所设计TMPS-HESM定子绕组要求。

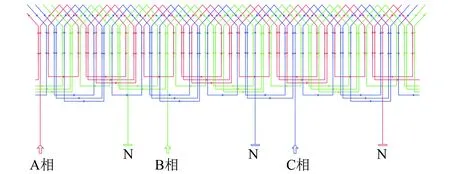
图4 电机定子绕组接线图

因此，该永磁电机与本文所设计TMPS-HESM在电磁负荷、电机尺寸、定子结构、定子绕组均一致，则使用该永磁无刷电机的定子模型为本文所设计TMPS-HESM的定子模型。

2.2 基于Maxwell建立TMPS-HESM转子及参数化模型

使用AutoCAD对电机转子模型按照尺寸要求进行绘制，然后导入Maxwell 2D有限元仿真软件进行材料设置，电机转子模型如图5(a)所示。将设置好的电机转子模型与用ANSYS RMxprt软件设计好的定子模型进行组合并进行仿真前处理设置，可以得到完整的电机Maxwell有限元仿真模型如图5(b)所示。

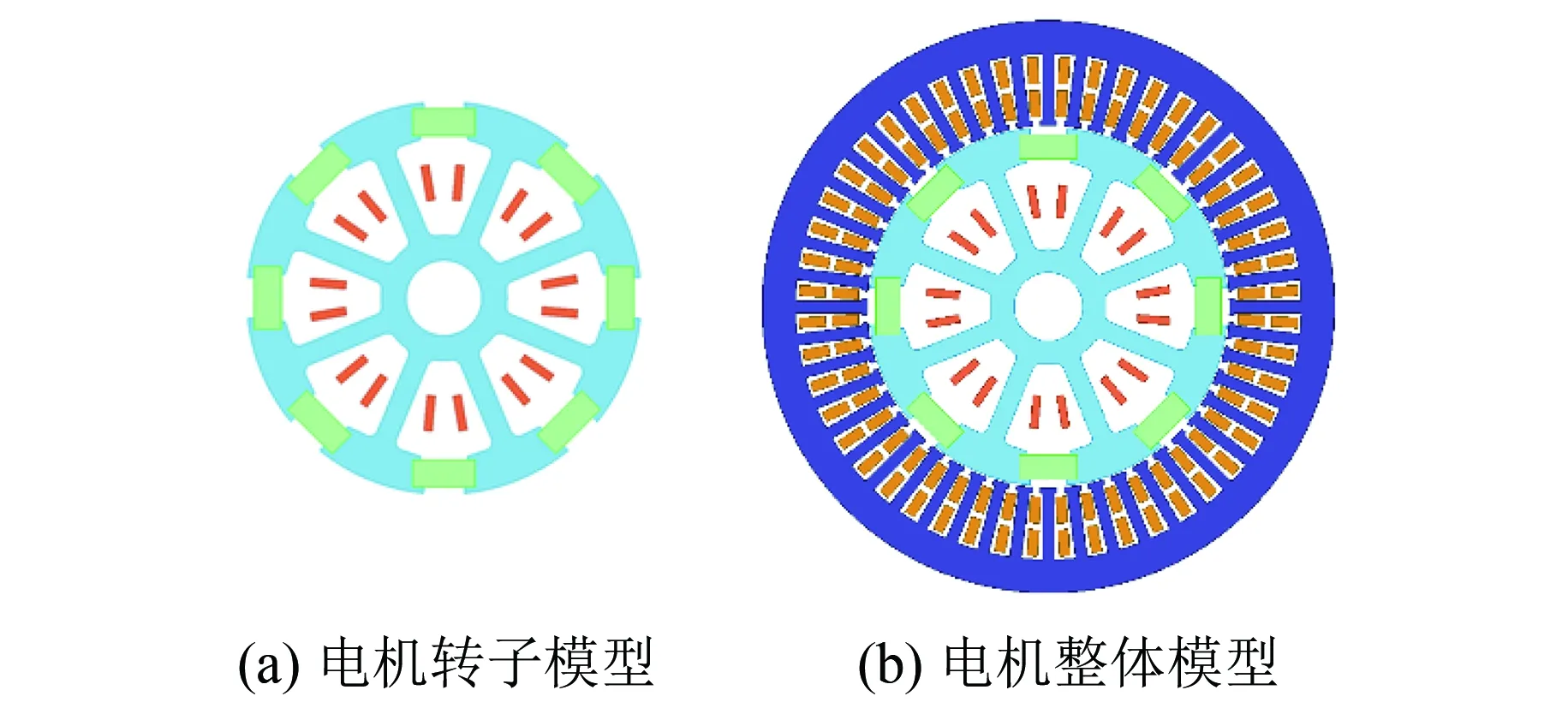
图5 TMPS-HESM有限元仿真模型

为了使所设计出的TMPS-HESM性能较好，需对TMPS-HESM进行多目标优化。如图6所示，对电机优化的参数进行参数化建模。转子部分的永磁体和转子极靴大小会对电机气隙磁密造成较大影响，从而影响电机输出转矩、齿槽转矩等性能，因此对电机永磁体长度l和宽度b以及转子极靴长度d和宽度w进行参数化建模。在定子和气隙部分，定子槽型的设计以及气隙大小也会对电机的性能造成较大影响，因此对电机槽口宽度bs0、槽口深度hs0、槽内深度hs1和气隙大小δ进行参数化建模。根据电机实际结构尺寸对以上参数化变量规定优化范围如表2所示。

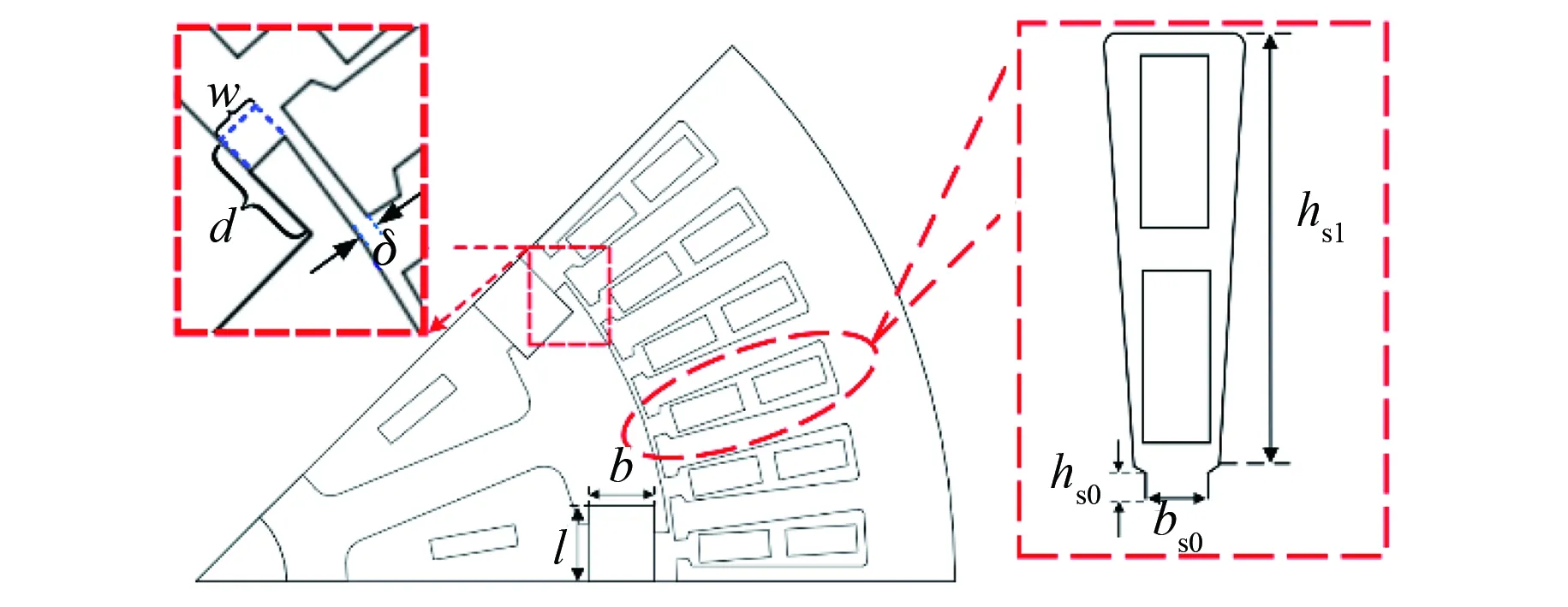
图6 TMPS-HESM参数化模型

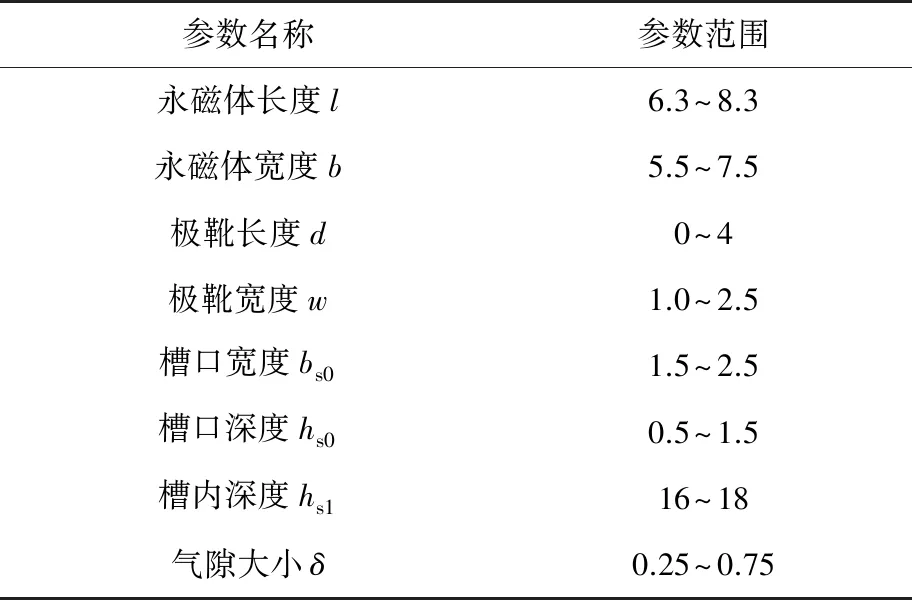
表2 参数化变量符号及优化范围 mm

2.3 基于PSO对TMPS-HESM设计分析

对于TMPS-HESM的优化设计涉及到8个输入变量和3个输出变量，如果采用有限元求解器的多参数优化需要大量运行时间和运算器内存。因此，将电机Maxwell有限元模型通过Workbench与Optislang进行联合仿真，使用Optislang中集成的智能算法对电机进行优化设计，联合仿真优化模块介绍如图7所示。为更有效寻找多输入变量和多输出优化目标的全局最优解集，采用具有收敛速度快、计算精度高和需调整参数少等优点的PSO[15]。分别设置初始种群为10个，PSO最大种群规模为400个，最大迭代次数为20次，突变率设置为30%。对粒子群进行变异操作，增强粒子群在迭代后期的突变能力，有利于其突破局部最优解。PSO优化流程如图8所示。

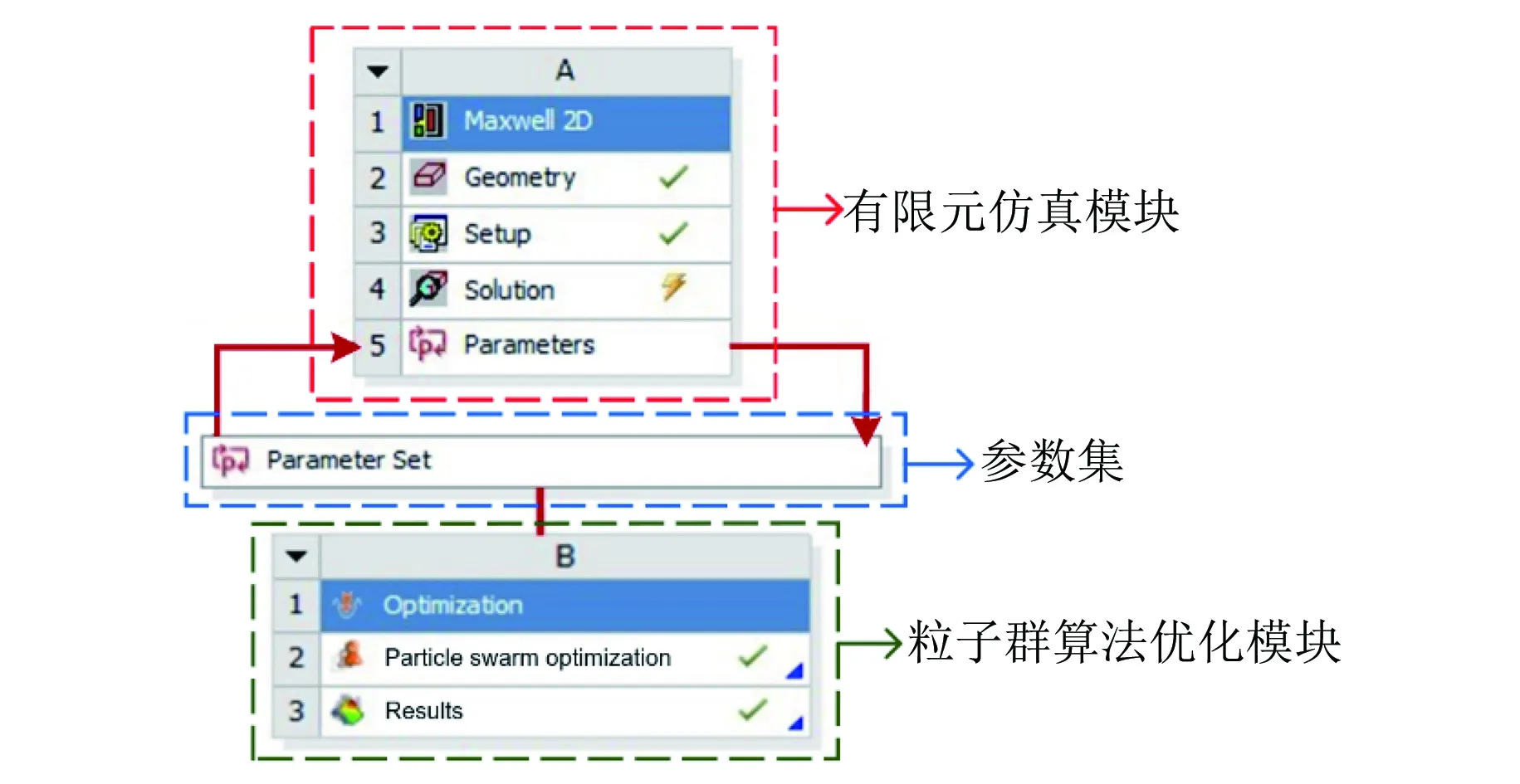
图7 联合仿真优化模块介绍

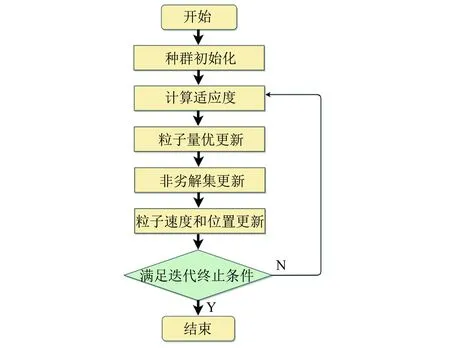
图8 PSO优化流程

在迭代过程中，每个粒子的速度和位置由局部最优点和全局最优点同时更新，PSO优化算法基本方程如下：

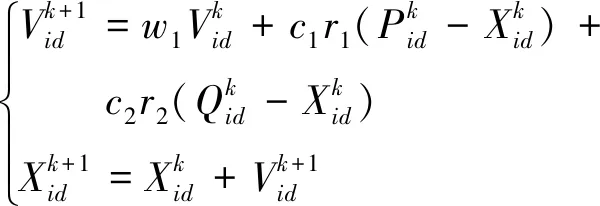
(6)

式中：Vid和Xid分别为第i个粒子在d维空间的速度和位置；k和d和w1分别为迭代次数、粒子搜索空间大小和惯性权重系数；r1和r2分别为在[0,1]之间的随机数；c1和c2分别为加速系数；Q和P分别为全局最优点与局部最优点。

为了加强优化初期的全局搜索，从而确保搜索后期的粒子收敛于全局最优解。将惯性权重系数w1设置成从w1max=0.9到w1min=0.4线性下降[16],w1表达式为

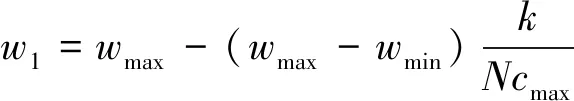
(7)

将加速系数c1和c2设置成采用异步时变的方式，c1、c2表达式分别为

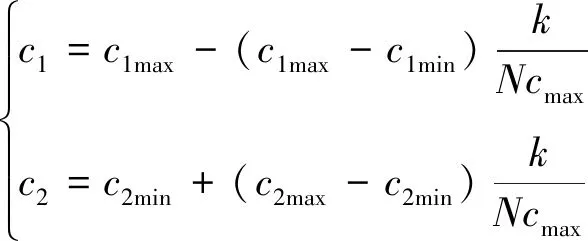
(8)

采用PSO进行多目标优化，以永磁体长宽、极靴长宽、槽口宽度和深度、槽内深度以及气隙距离这8个参数为输入变量，为了确保平均转矩、齿槽转矩和转矩脉动这3个输出变量均得到一定程度优化。分别将平均转矩最大、齿槽转矩最小和转矩脉动最小作为优化目标进行约束，具体目标函数和约束条件如下：

F(x)=[min(Tcog), min(Trip), max(Tavg)]，

TcogTavg0

(9)

式中：F(x)为多目标函数，Tcog0、Trip0分别为齿槽转矩、转矩脉动设置的数值上限，Tavg0为平均转矩设置的数值下限。

优化结果以Pareto 3D最优解集方式呈现，如图9所示，坐标轴分别表示齿槽转矩、平均转矩和转矩脉动。图9中数据点分别表示不同输入变量的粒子，深色圆点代表不符合约束条件的粒子，浅色圆点代表符合约束条件的粒子。三角形面代表Pareto前沿，Pareto最优解集位于Pareto前沿上，得到符合优化要求的解集一共有17个解，具体结果如表3所示。

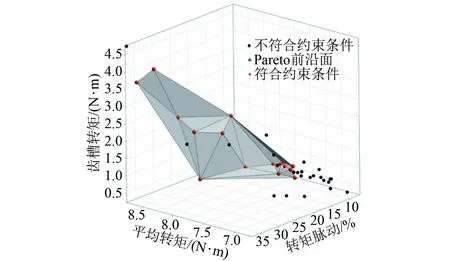
图9 Pareto 3D最优解集

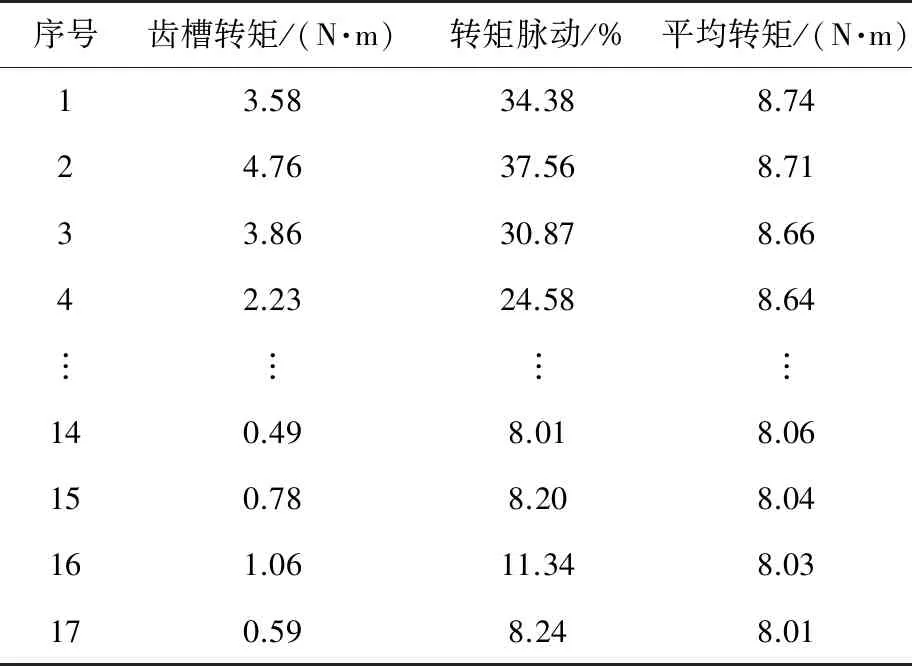
表3 Pareto最优解集

为了从Pareto最优解集中更客观地选取全局最优解，使用TOPSIS法对Pareto解集进行相对优劣评价[17-18]。TOPSIS法是一种客观高效的多目标决策分析方法，具体算法流程如下：

(1) 存在n个数据对象，m个评价指标时，每个指标以矩阵的形式呈现：

(10)

则初始矩阵为X=[X1X2…Xj]。

(3) 对数据进行归一化处理，一般采用平方和归一化，每个指标值消除量纲之后如下：

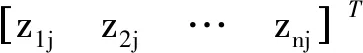
(11)

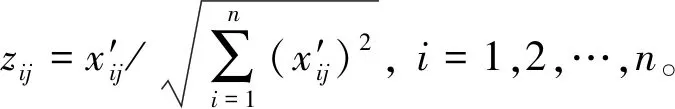
(4) 求解正负理想向量z+、z-如下：

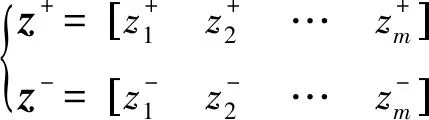
(12)

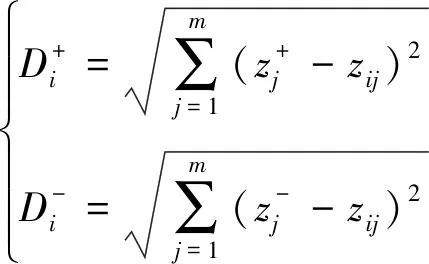
(13)

(6) 根据正负理想解距离计算相对接近度Ci如下：

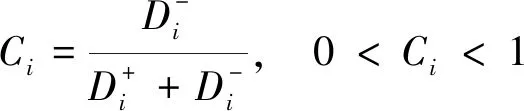
(14)

相对接近度Ci数值越大则表明TOPSIS法评价结果越好。

根据以上流程，对表3中的最优解集进行TOPSIS优化，以全局最优解为目标对象，评价指标分别为齿槽转矩、转矩脉动和平均转矩。通过对表3中数据正向化和归一化处理，将齿槽转矩、转矩脉动和平均转矩的最大值和最小值作为正负理想解，如表4所示。

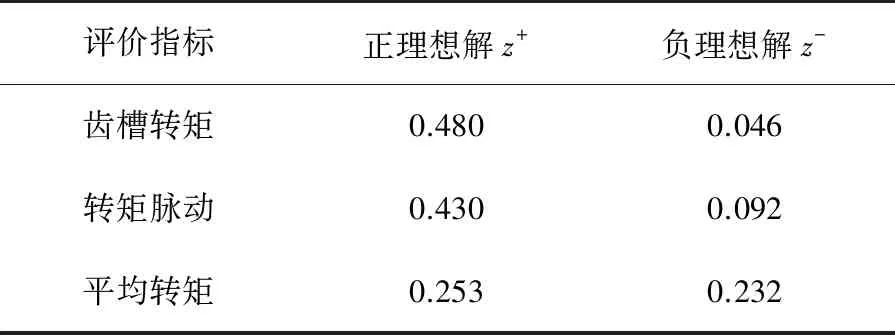
表4 正负理想解

根据正负理想解计算可得正负理想解距离和相对接近度如表5所示。由表5排序结果可知，应选定第2个解为全局最优解，从而确定最合理的永磁体长宽、极靴长宽、槽口宽度和深度、槽内深度以及气隙大小。

采用PSO和TOPSIS法得到全局最优解后电机输入参数和输出性能如表6所示，可以看出电机的各项参数取值合理，符合电机实际结构尺寸要求。同时在保持电机平均转矩满足要求的条件下电机齿槽转矩和转矩脉动较小，这对减少电机振动噪声和增强电机控制精度具有显著作用。

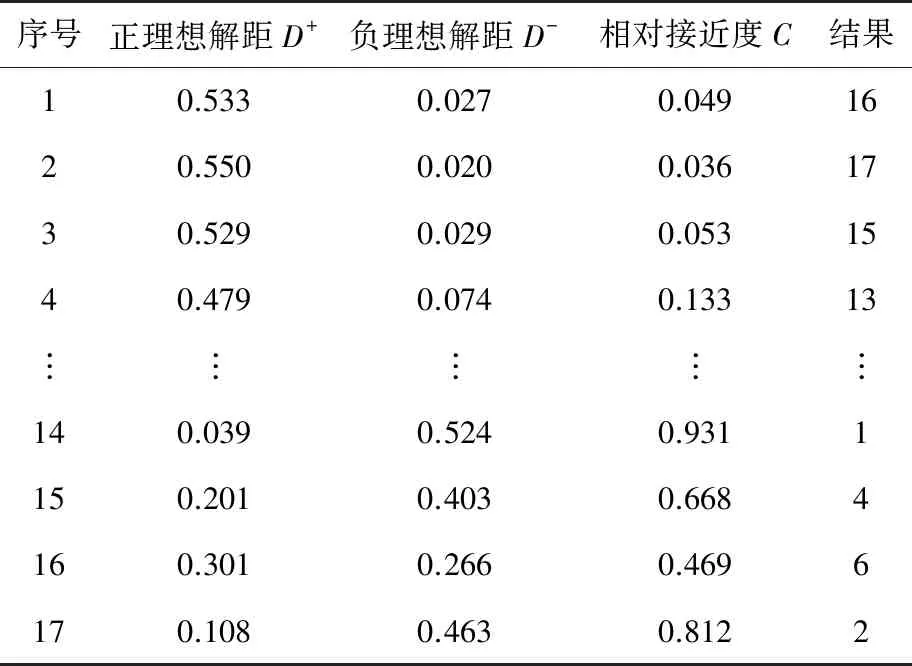
表5 TOPSIS评价计算结果

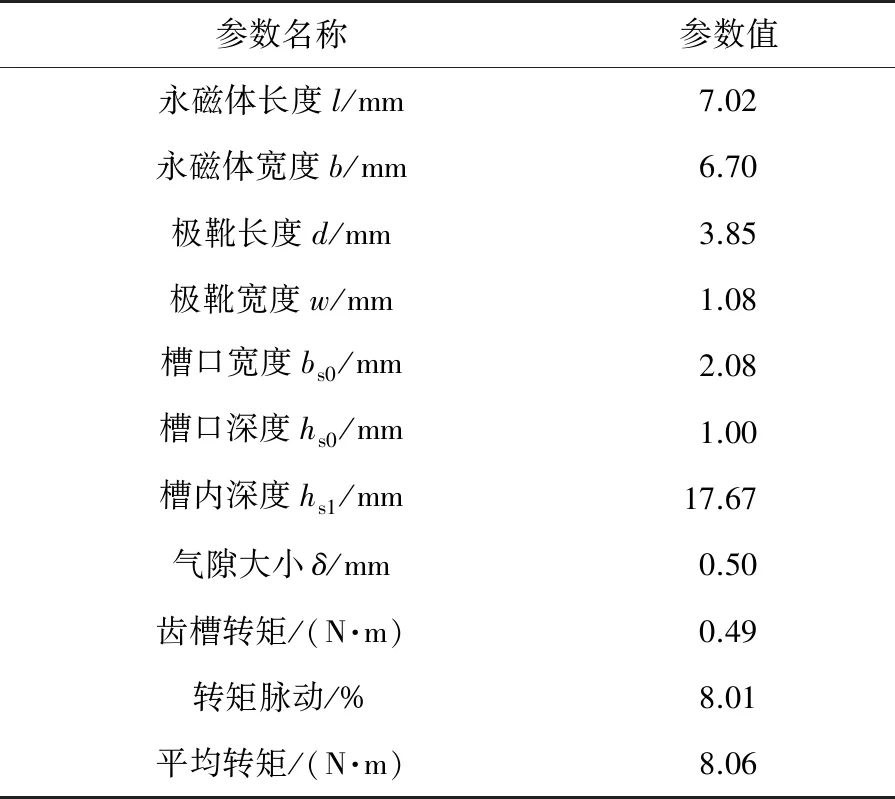
表6 PSO和TOPSIS法求得最优解对应的电机参数

3 TMPS-HESM电磁性能分析

为了验证本文所设计电机满足设计要求通过Maxwell有限元仿真软件研究了本文所设计的TMPS-HESM的电磁性能。

图10和图11分别为TMPS-HESM在不同励磁电流条件下电机的磁力线分布图和电机磁密云图，分别对其进行分析，验证等效磁路模型和调磁原理理论推导的正确性。

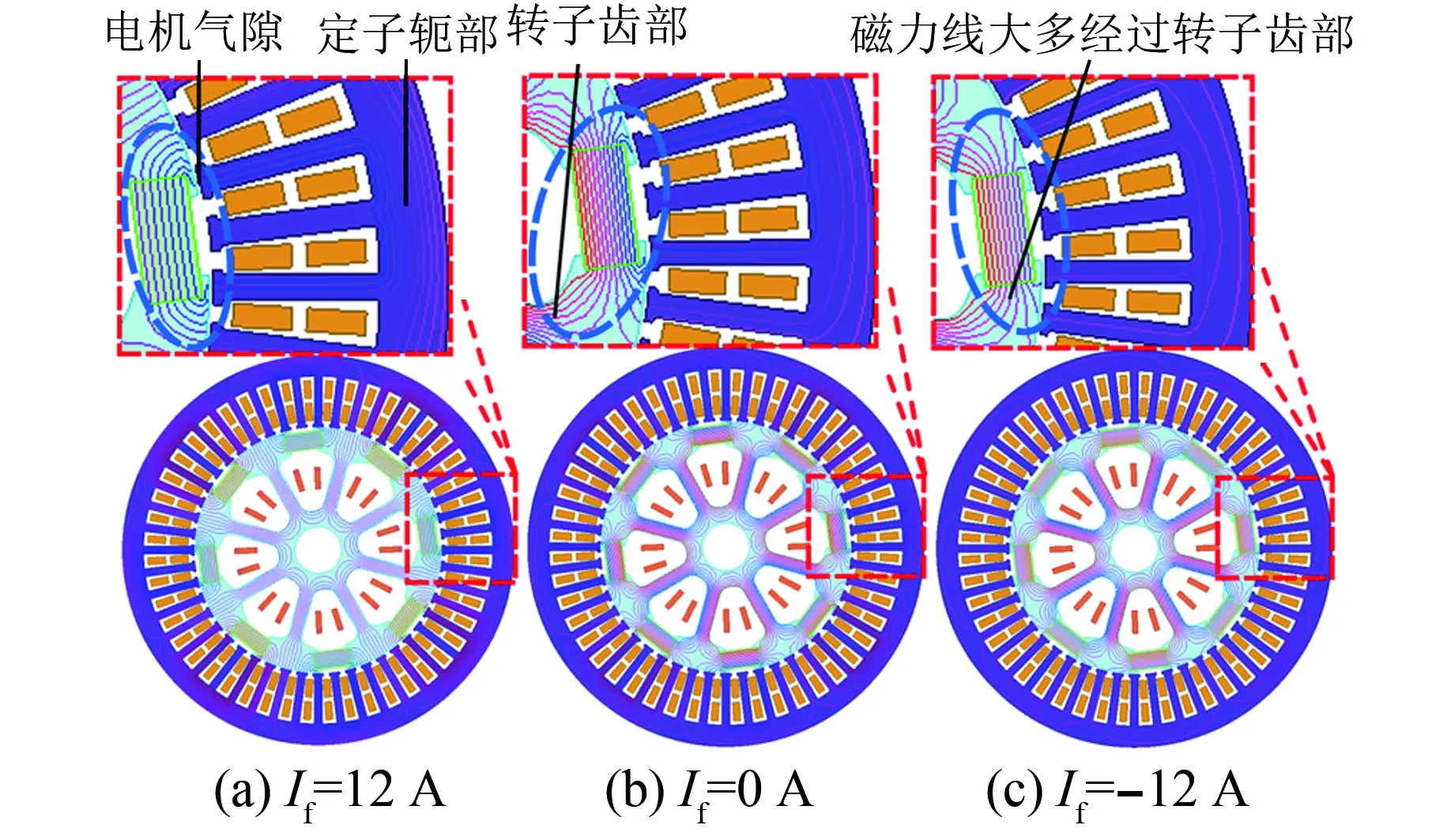
图10 电机磁力线分布图

当励磁电流If=12 A时，电机正向励磁时候，绝大多数磁力线到达电机气隙部分，通过电机定子形成闭环，此时电机磁密云图的气隙处磁场较大。

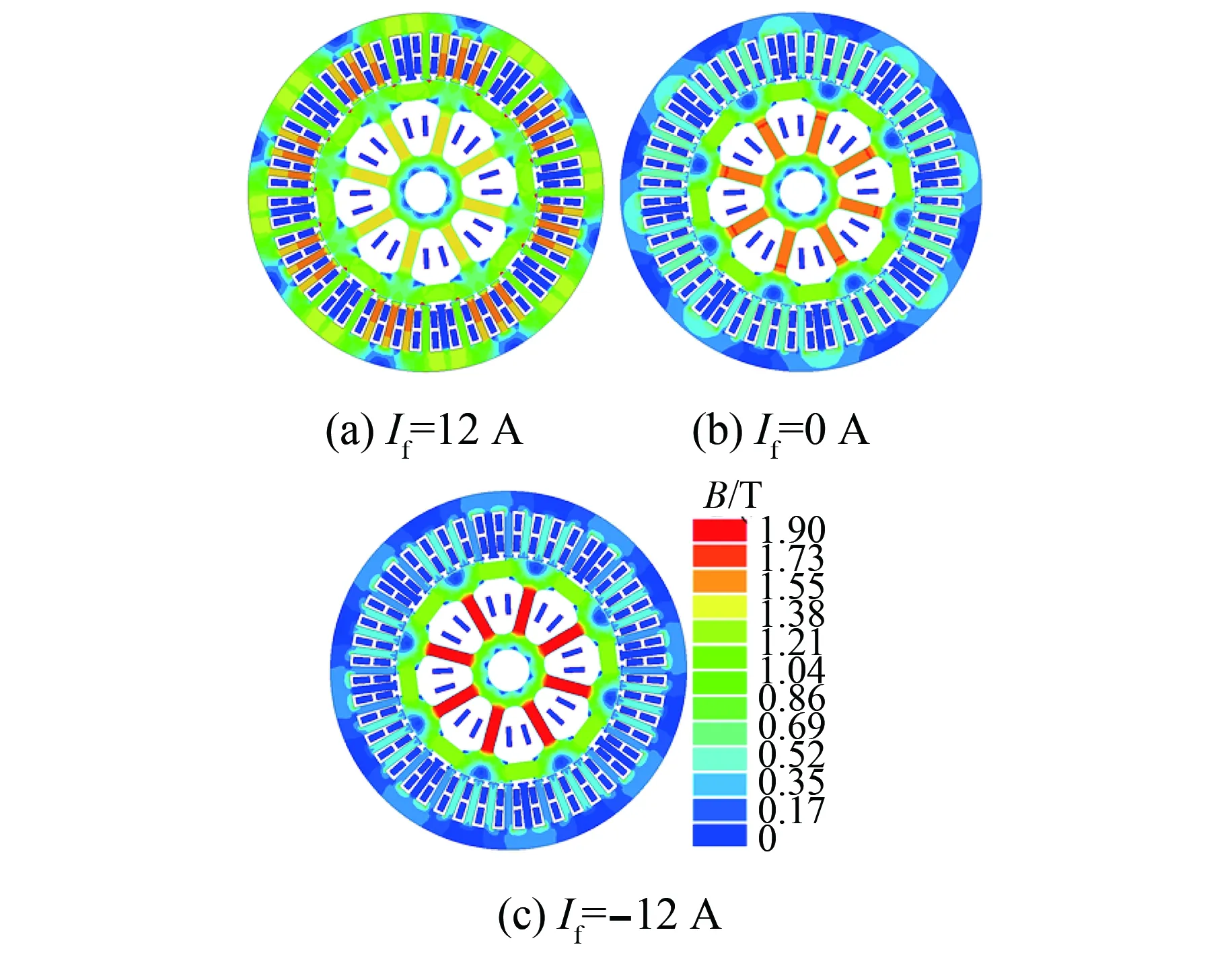
图11 电机磁密云图

当励磁电流If=0 A时，部分磁力线通过转子齿部形成转子磁短路现象，此时经过电机气隙处的磁力线较少，电机磁密云图的气隙处磁场也较小。

当励磁电流If=-12 A时，由于电励磁绕组负向励磁的作用，加剧了磁力线通过转子齿部形成的磁短路现象，磁力线会集中在转子齿部，形成饱和磁场，此外剩余的极少数磁力线仍会通过电机气隙部分，这也解释了当If=-12 A时，气隙磁通密度仍有一个较小的幅值。

由图12电机效率MAP可以看出，在额定转速3 500 r/min的区域，电机效率高达95%，并且电机高效率区域较广。电机在低转速区域可提供较大的转矩，同时电机具备良好的弱磁升速能力。

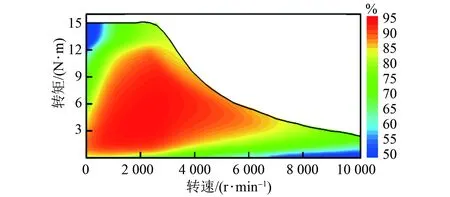
图12 电机效率MAP图

由图13和图14可以看出，当电机通入正向励磁电流时，电机气隙磁密和空载反电动势显著增大，该电机具有良好的增磁增矩能力。当电机通入负向励磁电流时，气隙磁密幅值减小的幅度很小，这是由于TMPS-HESM具有特殊的磁短路转子结构。电机气隙磁密的变化规律与上文等效磁路模型理论分析一致，且符合调磁范围0.2～0.9 T要求。

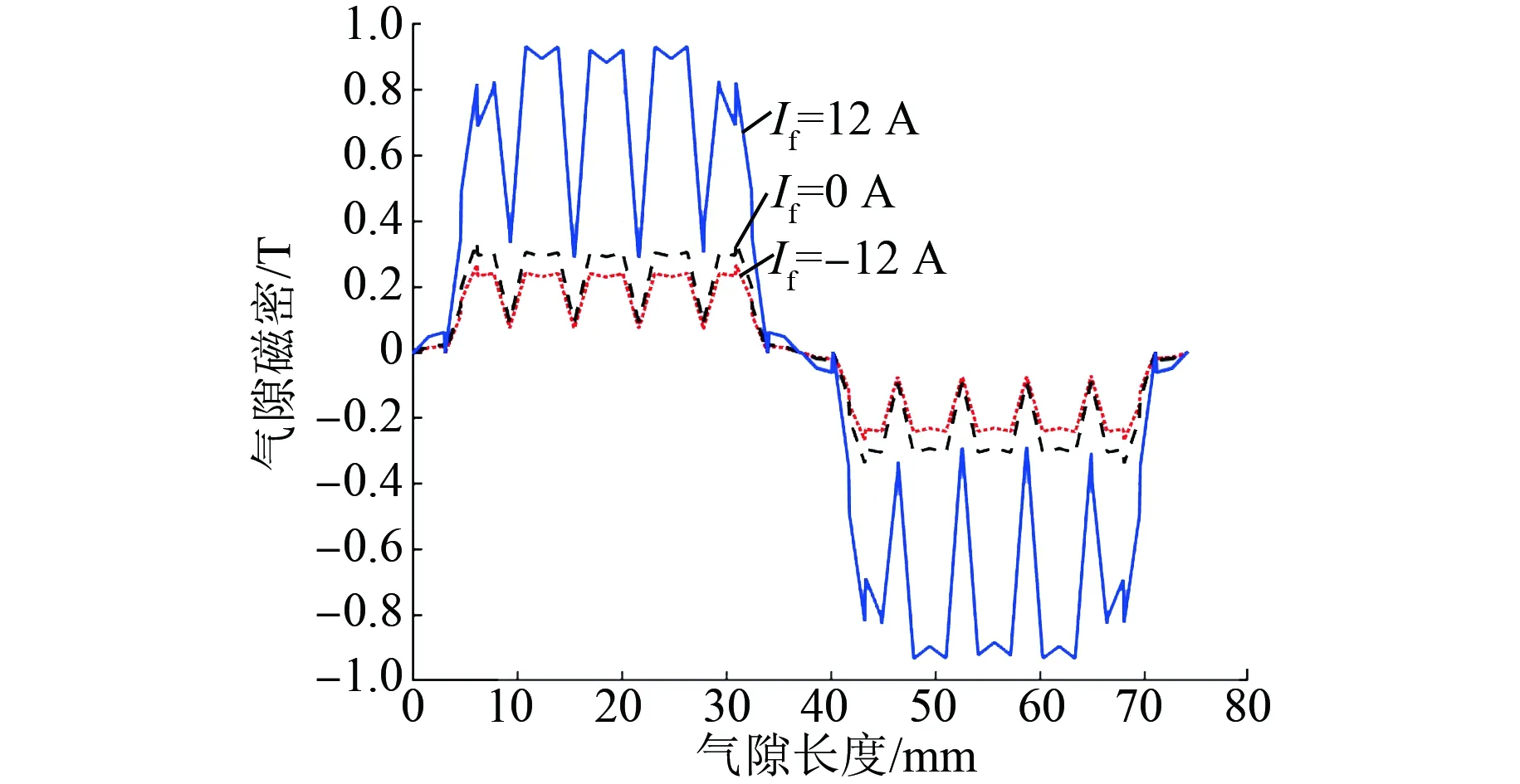
图13 电机气隙磁密

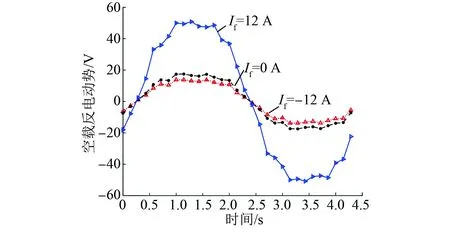
图14 电机空载反电动势

由图15和图16可知，在电机通入正向励磁电流时平均转矩和齿槽转矩明显增加，平均转矩从3.90 N·m增至8.06 N·m，齿槽转矩从0.17 N·m增至0.49 N·m。电机通入负向励磁电流时平均转矩和齿槽转矩下降程度很小。电机的转矩脉动在If=-12 A时为9.74%，在If=0 A时为9.26%，在If=12 A时为8.01%，电机转矩脉动和齿槽转矩均符合转矩脉动小于10%和齿槽转矩小于0.5 N·m的设计要求。

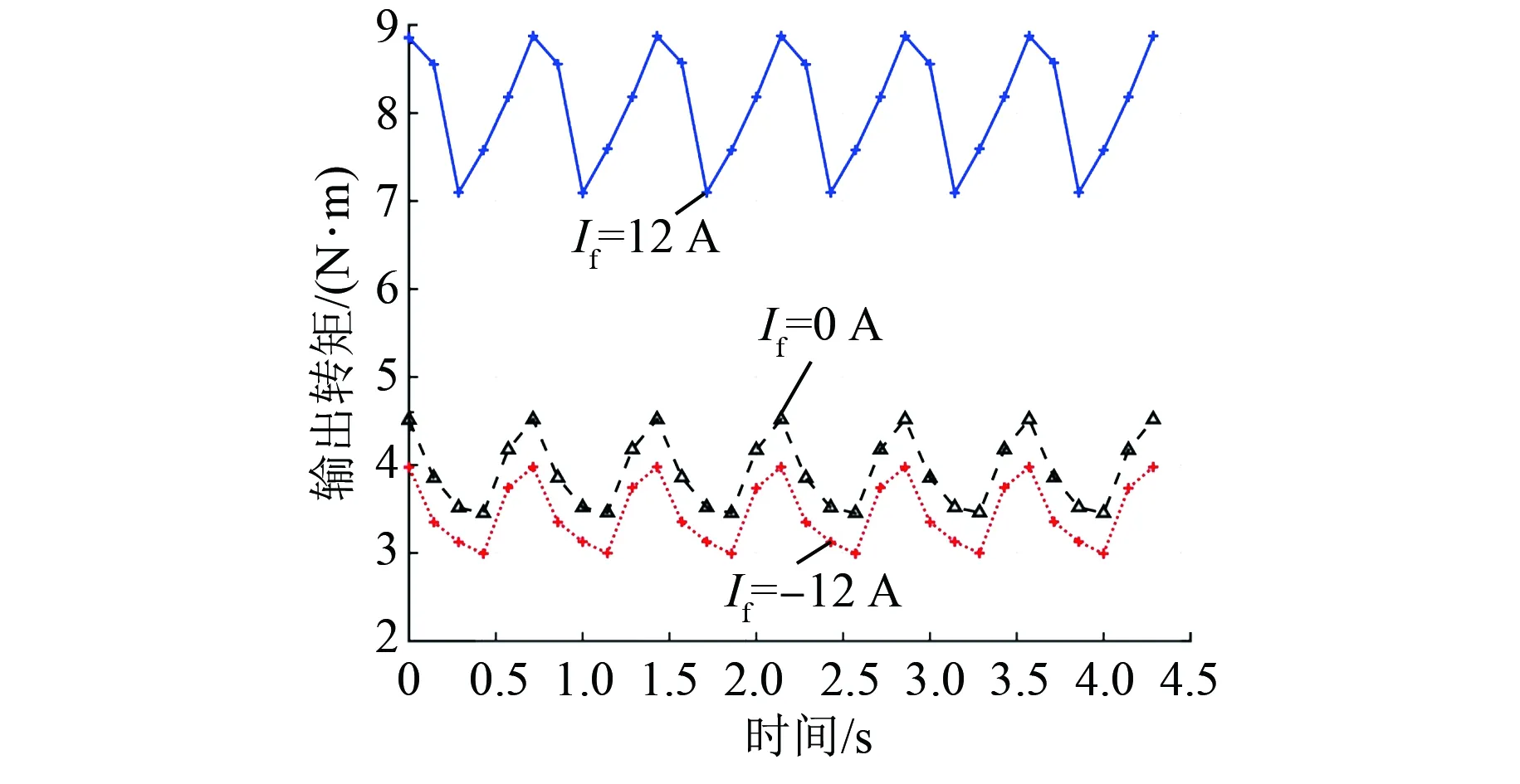
图15 电机输出转矩

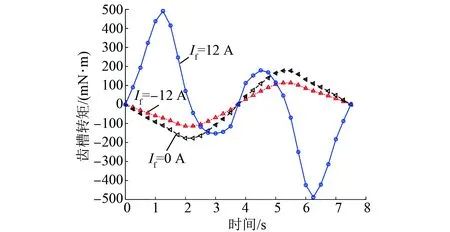
图16 电机齿槽转矩

因此，本文所设计电机具有良好的调节磁场能力和效率，通过使用PSO和TOPSIS法，使设计的电机具有较为合适的平均转矩和较小的转矩脉动和齿槽转矩，总体方案满足TMPS-HESM的设计要求。

4 结 语

本文系统地提出了一种基于PSO的TMPS-HESM联合仿真设计方法，并通过相关有限元仿真试验验证了电机性能符合设计要求，可以得到以下结论：

(1) 基于PSO的TMPS-HESM联合仿真设计方法，解决了ANSYS RMxprt、Motor-CAD等现有电机磁路设计软件无法直接设计TMPS-HESM的问题，有效提升类似电机的设计效率和准确性。

(2) 通过Maxwell & Workbench & Optislong联合仿真，使用Optislang PSO对电机进行优化设计，有效提升了电机多目标优化设计的效率。