基于全域解析法的外转子轮毂永磁同步电机多目标优化

马志敏， 齐晓刚， 王少勃， 景弋洋， 何 彪， 曹海东

(1.浙江万安科技股份有限公司，浙江 绍兴 311800；2.北京天源博通科技有限公司，北京 100000；3.华南理工大学 电力学院，广东 广州 510641；4.上海电器科学研究所(集团)有限公司，上海 200063；5.上海大学 机电工程与自动化学院，上海 200433)

0 引 言

新能源汽车驱动系统的集中式布置是当下主流，但从技术发展角度而言，分布式一体化结构则是未来趋势。在发挥分布式驱动优势方面外转子轮毂电机扮演着重要角色。外转子轮毂电机适用于A级和A0级新能源乘用车、轻型商务车、物流车等具有分布式驱动结构的电动汽车。这种分布式结构使电动汽车具有空间布置自由度大、能量利用效率高和动力学控制性能优异等技术优势，成为最具吸引力的电驱动发展方向之一[1]。

电机气隙磁场分布的准确计算是设计电机并分析其性能时所需的基本条件。计算磁场时通常采用精度较高的有限元法，但其剖分复杂计算耗时较多[2]。全域解析法需要一定的前提假设，可分析的电机几何结构较单一，但能明确地反映参数对磁场的作用。又因为其不需要大量的前处理，降低模型调整难度的同时加快了计算速度[3-6]。因此,全域解析法是电机性能预评估和设计优化的有效工具。

车用永磁电机的优化存在变量多、非线性、数学模型复杂等特点，且需满足一定的约束条件，实现电机效率、转矩、功率密度、转矩脉动等指标达到最优。随着智能控制理论的不断发展，已有多种智能算法应用于电机优化设计中，典型的优化方法包括：遗传算法、免疫算法、蚁群算法及粒子群算法等[7]。文献[8]在搭建参数解析表达式的基础上应用多种群遗传算法实现了环形绕组无铁心的永磁直线电机多目标的设计。文献[9]应用混沌遗传算法实现了永磁电机的多目标优化，并对比优化前后各参数。文献[10]将永磁电机的基本电磁设计和免疫遗传算法合理结合,实现了螺杆泵直驱永磁电机电磁方案的优化，所设计电机最终获得了较好的电磁性能。文献[11]基于磁场解析模型与遗传算法实现了轴向磁通电机的多目标优化，降低了电机的有效成本，提高了电机的电磁转矩，验证了解析模型与遗传算法结合的优化方法有效性，但未对外转子轮毂永磁同步电机(PMSM)进行相关优化研究。文献[12]应用量子遗传算法，以电机有效质量、材料成本和功率损耗为优化目标，建立了包含8个设计变量和5个约束的数学模型，对电机进行优化设计,降低了电机有效质量、材料成本和功率损耗，提升了电机的效率特性，但在优化过程中未能应用解析模型进行计算，因此增加了优化时长。

本文基于全域解析法对外转子PMSM的空载反电动势、气隙磁密、齿槽转矩、转矩以及转矩脉动等性能求解计算；在此基础上应用第二代非支配排序遗传算法(NSGA-Ⅱ)对电机永磁体用量、效率和转矩脉动进行多目标优化，与电机初始方案相比，优化后的方案在满足电机出力的情况下，降低了电机的转矩脉动以及提升了电机的运行效率。

1 外转子轮毂PMSM解析计算

1.1 永磁体充磁与电机解析模型

本文的电机模型中永磁体磁钢采用平行充磁磁化方式，充磁方向如图1所示。

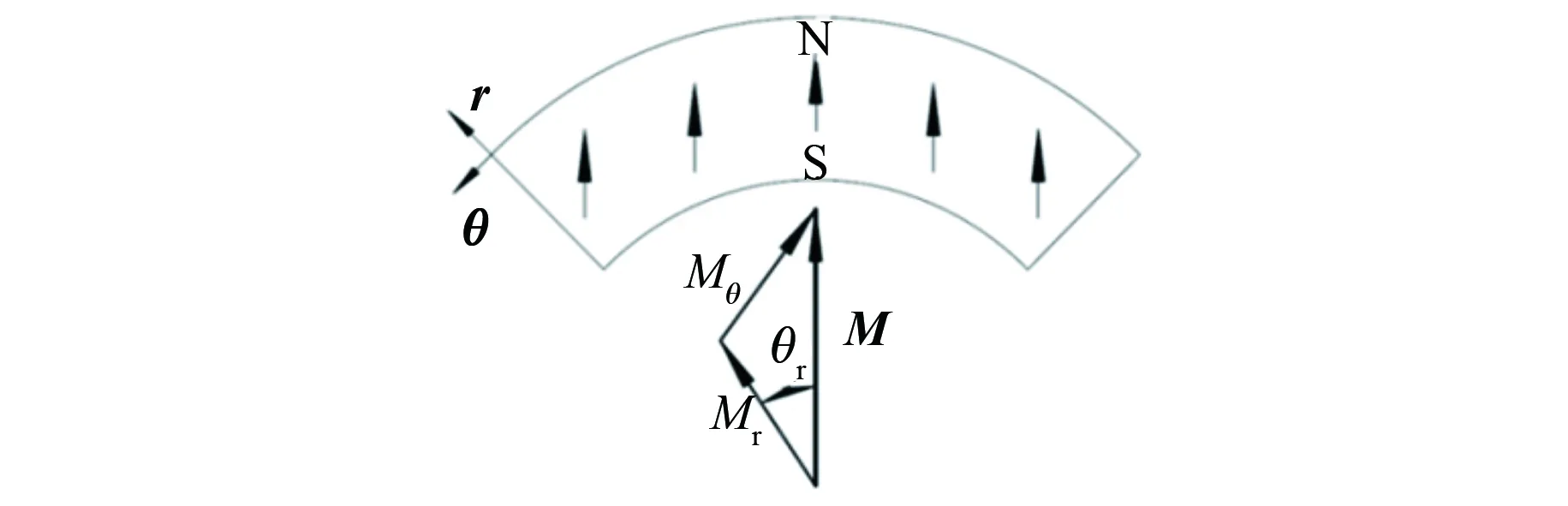
图1 平行充磁磁化方向

永磁体磁化强度M在极坐标系下的表达式如下：

M=Mrr+Mθθ

(1)

式中：r为磁化强度的径向分量;θ为磁化强度的切向分量。

当平行充磁时有如下表达式[5]：

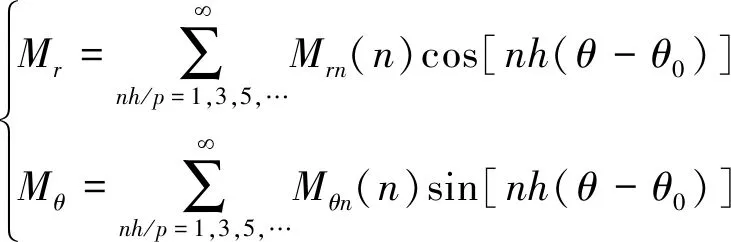
(2)

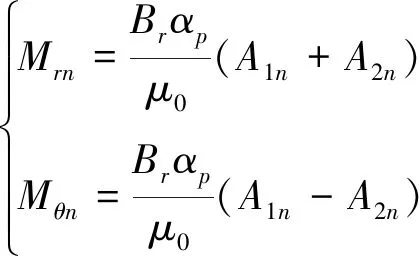
(3)

式中:h为槽数Q与极对数p的最大公约数；n为永磁体磁化强度谐波分量次数；θ0为设定的初始基准位置与永磁体位置间的夹角；Br为永磁体剩余磁场强度；αp为永磁体极弧系数；μ0为真空磁导率;A1n、A2n为系数。

系数A1n和A2n表达式如下：

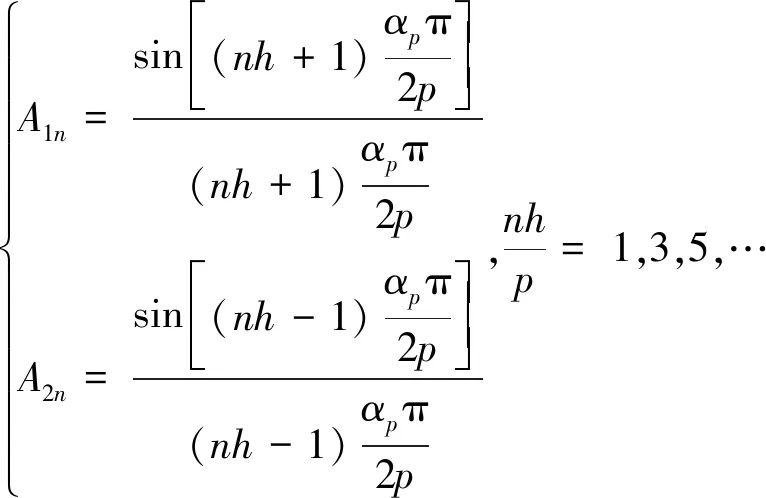
(4)

在全局解析法电机模型中，空载时整个电机可分为4个求解区域：气隙区域1、采用不同方式充磁的永磁体区域2、i(槽口)部分区域Si以及j(槽身)部分区域Sj。由于采用双层绕组， 若要计算电枢反应磁场，j槽部分Sj又可分为下层区域Sj1和上层区域Sj2,i=j=1,2,…,Q。图2所示为电机求解区域几何模型。

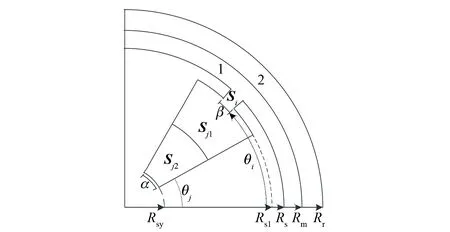
图2 电机求解区域几何模型

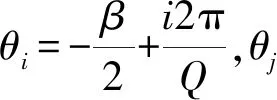
根据此模型，在采用全局解析法计算空载磁场时还需做出如下假设：

(1) 用二维极坐标系进行磁场运算，忽略端部效应；

(2) 铁心磁导率μ=∞；

(3) 永磁体相对磁导率μr=1；

(4) 定子半闭口扇形槽，槽内无电流。

1.2 空载磁场计算

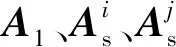
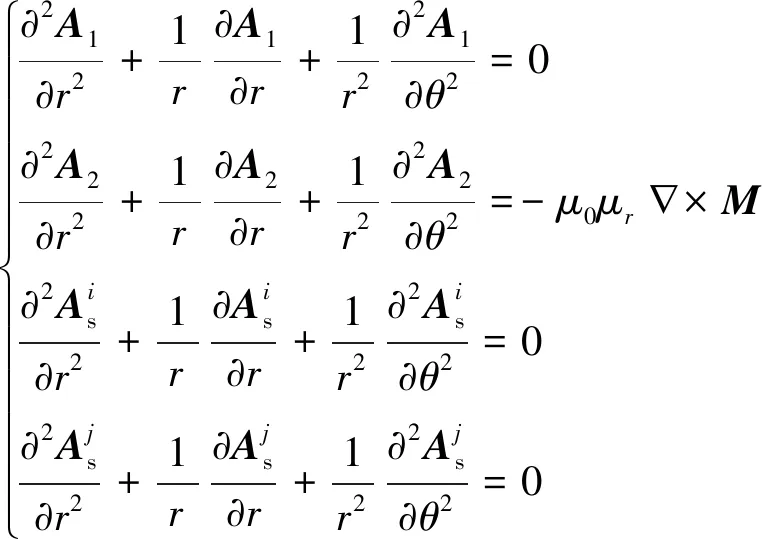
(5)

由电磁场定律可得图2中各子域边界条件为

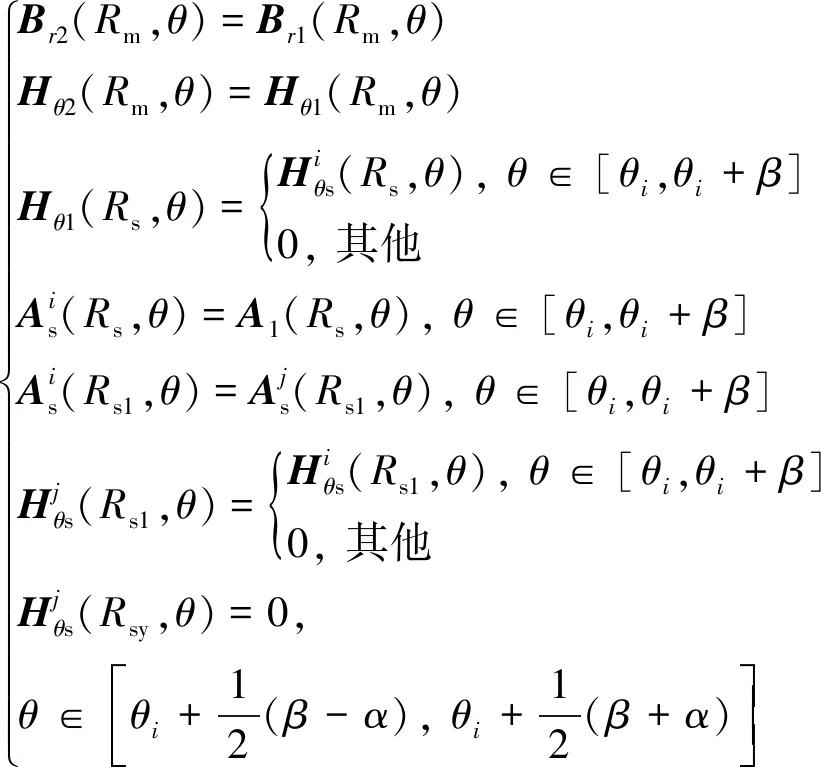
(6)

式中:B为磁通密度;H为磁场强度;下标r和θ分别为径向和切向分量；数字下标1、2为气隙区域、永磁体区域;上标i、j分别为第i、j槽区域。

对式(4)使用分离变量法，得各区域矢量磁位通解表达式如下：

(C1nrnh+D1nr-nh)sin(nhθ)]

(7)

(C2nrnh+D2nr-nh)sin(nhθ)]+

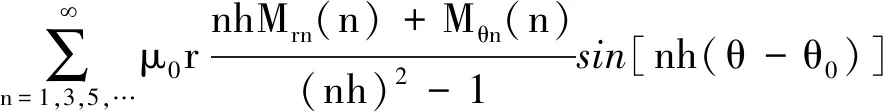
(8)

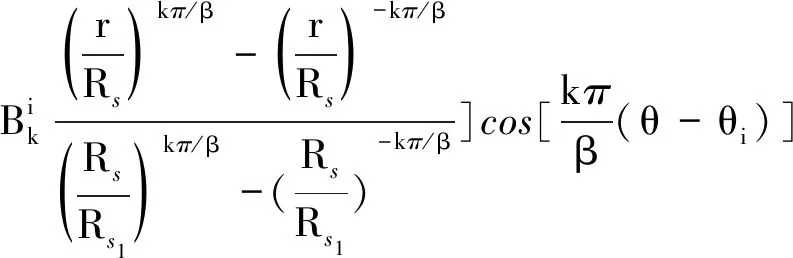
(9)

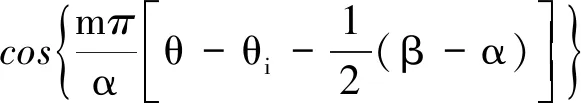
(10)

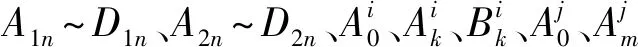
在极坐标系下，由磁矢位和磁密的关系，在气隙区域内对求得的矢量磁位按式(10)求偏导数可解得径向和切向上的磁通密度分量：

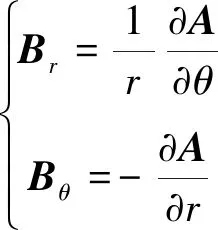
(11)

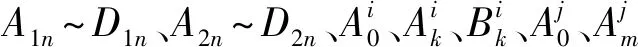
计算齿槽转矩时采用麦克斯韦应力张量法，具体表达式如下所示：

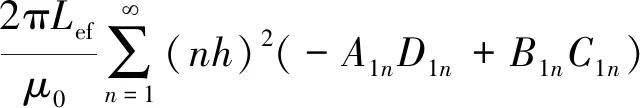
(12)

槽内采用双层绕组时的空载磁链计算式如下所示：

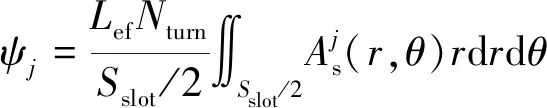
(13)

对空载磁链微分可得到感应电动势如下：

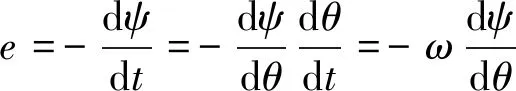
(14)

式中:Lef为电机轴向计算长度;Re为计算转矩时选取的积分路径半径;Nturn为双层绕组中每层绕组的导体数;Sslot为槽区域j的面积;ω为外转子电机旋转机械角速度。

1.3 负载磁场计算

在电枢反应的计算过程中，令永磁体不充磁，由于永磁体的磁导率与空气非常接近，可将其和气隙联合在一起作为等效气隙处理。

在用解析法计算定子开槽时气隙磁场时对磁场做如下假设：

(1) 用二维极坐标系进行磁场运算，忽略涡流与饱和效应。

(2) 定子与转子的铁心磁导率μ=∞。

(3) 永磁体内无磁化强度，在其位置用磁导率与永磁磁极相同的材料填充，计算中处理为永磁体等效气隙，与气隙合并形成大气隙。

(4) 定子半闭口扇形槽，槽内电流均匀分布。

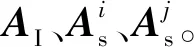
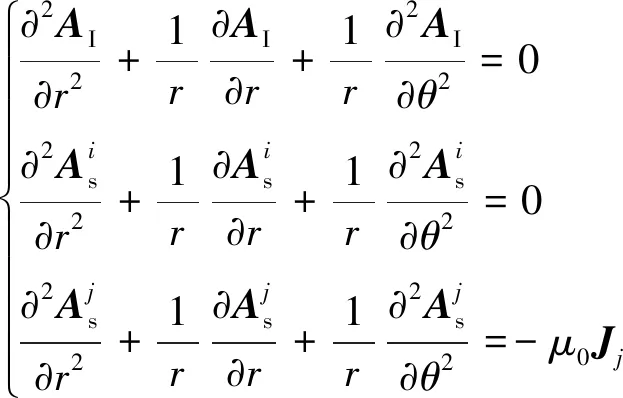
(15)

式中:Jj为第j槽内的电流密度。

关于全域解析法对负载磁场的计算与式(15)的计算方法在文献[13]中有详细的介绍，本文的负载磁场计算方法与该文献基本一致，不再详细介绍。

2 NSGA-Ⅱ设计

本文采用NSGA-Ⅱ的基本理论，对车用外转子轮毂PMSM的优化目标函数、优化变量、约束条件进行分析确定。

2.1 NSGA-Ⅱ基本理论

NSGA-Ⅱ是由Deb等[14]提出的一种多目标进化算法，其具有良好的解扩散性和收敛性。该算法在非支配排序遗传算法(NSGA)的基础上提出了快速非支配排序，有效地将算法复杂度从O(MN3)降到O(MN2)。其中，M为目标个数，N为种群规模。NSGA-Ⅱ采用精英策略避免了父代种群中优秀个体的遗漏。此外，在种群个体的选择上，NSGA-Ⅱ提出了拥挤度比较算子，不需要人为定义的参数就可保持群体成员之间的多样性。NSGA-Ⅱ算法的基本优化流程如下：

步骤1，随机产生个体规模为N的初始种群Pt(父代种群)，计算每一个体的目标函数值并按照非支配排序进行分类，使每个解获得与其非支配级别相等的适应度(或等级)。然后通过选择、交叉、变异算子得到规模为N的子代种群Qt。

步骤2，遵循精英主义策略，将父代种群Pt与子代种群Qt合并为种群Rt(个体数量为2N)。对Rt进行快速非支配排序来生成非支配集FX(X=1, 2, …,n)并计算其拥挤距离，然后从最优非支配集F1开始依次根据拥挤度比较算子选出N个个体组成新的父代种群Pt+1。

步骤3，新的父代种群Pt+1开始新一轮的迭代，通过步骤1创建出新的子代种群Qt+1，二者再次合并形成种群Rt+1执行步骤2。NSGA-Ⅱ算法不断重复此过程直至满足约束条件为止，如图3所示。

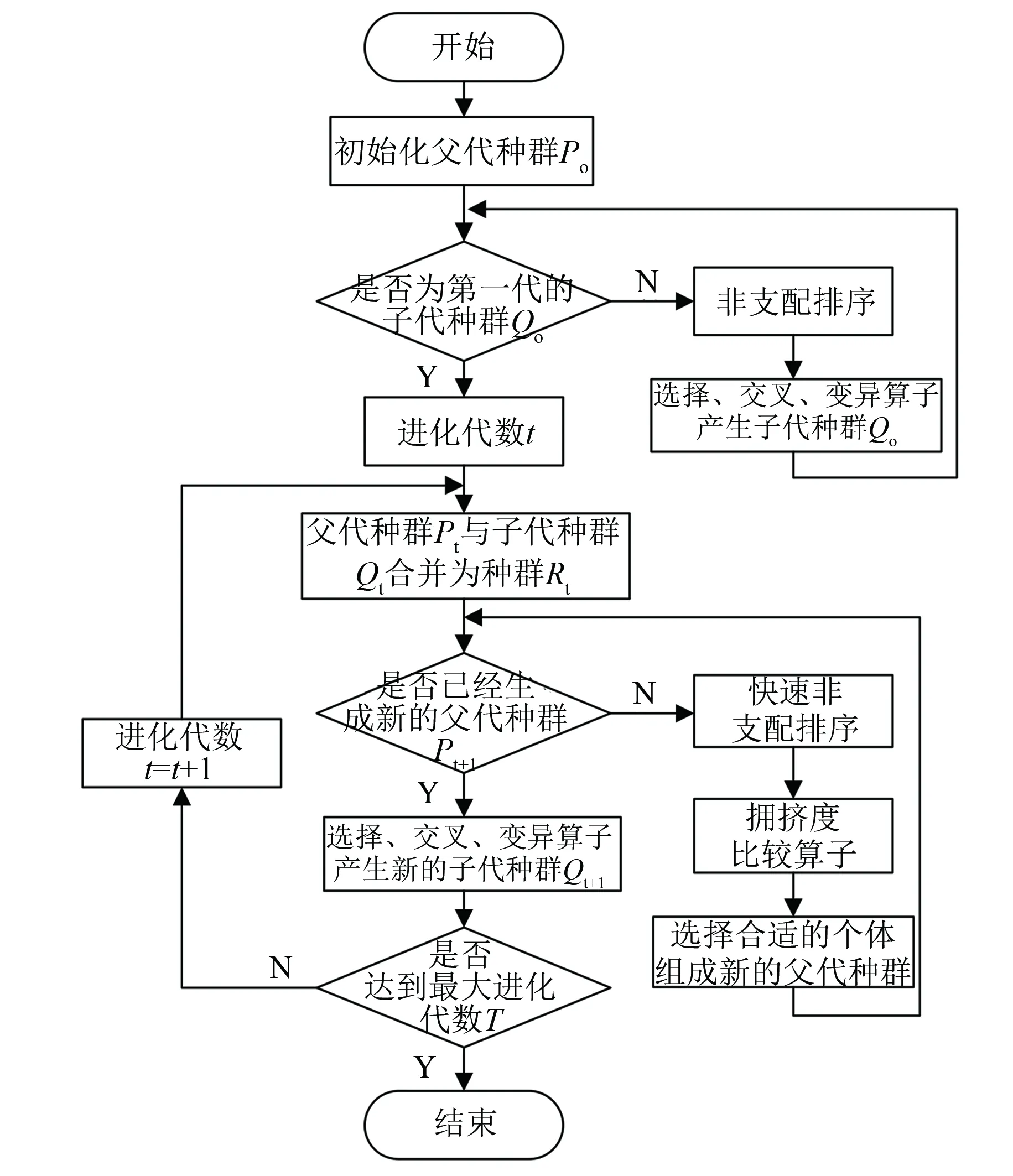
图3 NSGA-Ⅱ算法的流程图

2.2 目标函数、优化变量及约束函数确定

确定目标函数是电机优化设计中最重要的决策之一，体现了设计者的设计意图，同时也是电机设计的关键性能指标。

效率、转矩脉动作为电机的重要指标，体现了驱动电机运行节能优劣及波动性。低振动、低噪音电机往往要求低的转矩脉动，永磁体用量直接关系到电机的成本。因此本文将效率、转矩脉动及永磁体用量作为电机设计优化目标。

电机结构参数非常多，而且自由度较大，无法全部都考虑到，因此要根据所列目标函数选取关键参数作为电机的优化变量。根据目标函数选取气隙厚度、永磁体极弧系数、槽口角度以及永磁体厚度作为电机优化变量。

NSGA-Ⅱ作为一种群体搜索算法，其搜索是在选定的变量设计空间进行的。因此,必须给出各优化设计变量的上限值、下限值。本文在采用NSGA-Ⅱ进行优化时，选取各变量值上下限如表1所示。

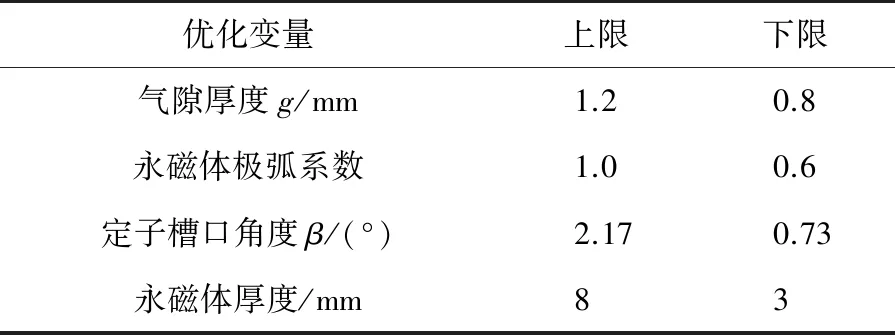
表1 电机模型优化设计变量

电机优化设计问题中的约束除了优化变量变化范围的一般约束，还有电机的性能约束，电机的性能约束是根据电机设计的技术性能指标来确定的，均是优化变量的函数。

本文将工程设计中对电机性能要求高的平均转矩Tavg作为电机优化设计问题的性能约束条件，可用式(16)来表示其约束函数：

Tavg≥450 N·m

(16)

式中：Tavg以转矩1个周期的平均值为基准。

3 原样机解析计算、有限元仿真对比及多目标优化

3.1 原样机结构参数

本文样机为一台外转子表贴式轮毂PMSM，各部件结构如图4所示，具体参数如表2所示。

图4 样机各部件结构

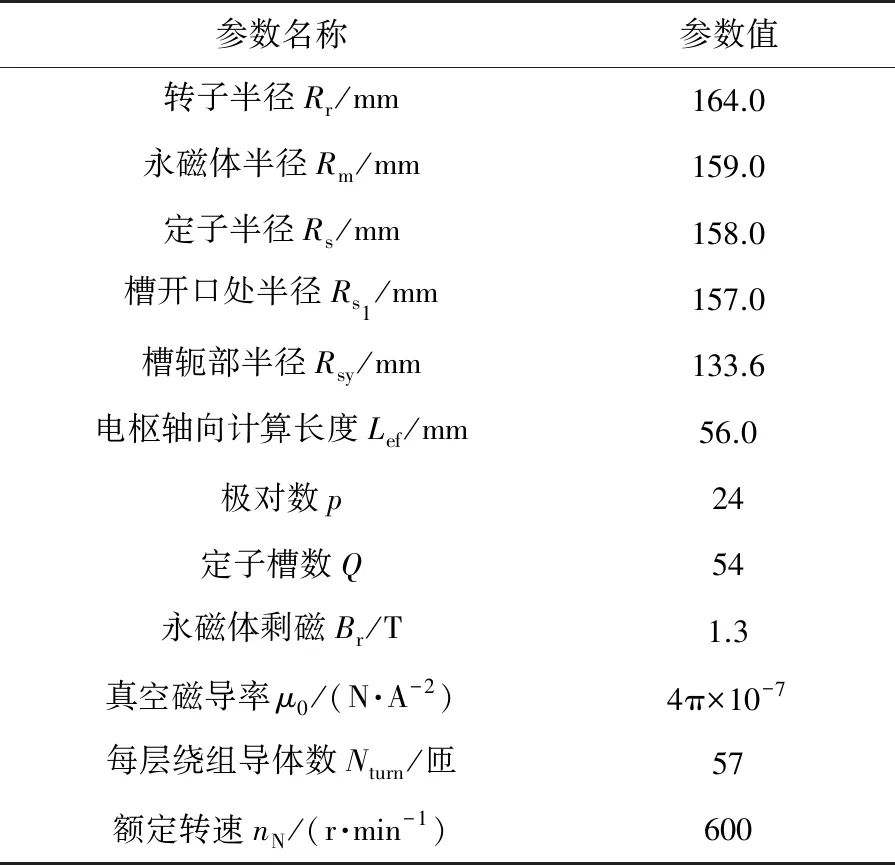
表2 电机模型参数

3.2 解析法与有限元法对比

将解析法与有限元软件计算结果进行对比。本文样机为48极54槽分数槽电机,单元电机为8极9槽,因此仅计算六分之一电机模型即可。以r=(Rm+Rs)/2为半径，提取空载气隙磁密解析解和有限元解比较结果如图5所示。

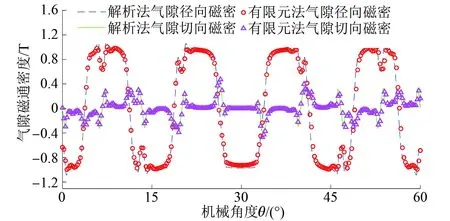
图5 空载气隙磁密波形对比

由图5可知，由于聚磁效应解析法相对有限元法在齿边缘的计算结果稍有偏差，但整个磁密波形基本吻合。而空载磁密的正确可以反映出其余特性的正确性，从而证明了全局解析法的正确性，因此空载磁密可以进一步地作为电机多目标优化。

该电机的齿槽转矩周期为(24×360)/LCM(2p,Q)=20°，LCM(2p,Q)为极数2p与槽数Q的最小公倍数。原尺寸下一个周期内的齿槽转矩解析法和有限元计算波形比较如图6所示。

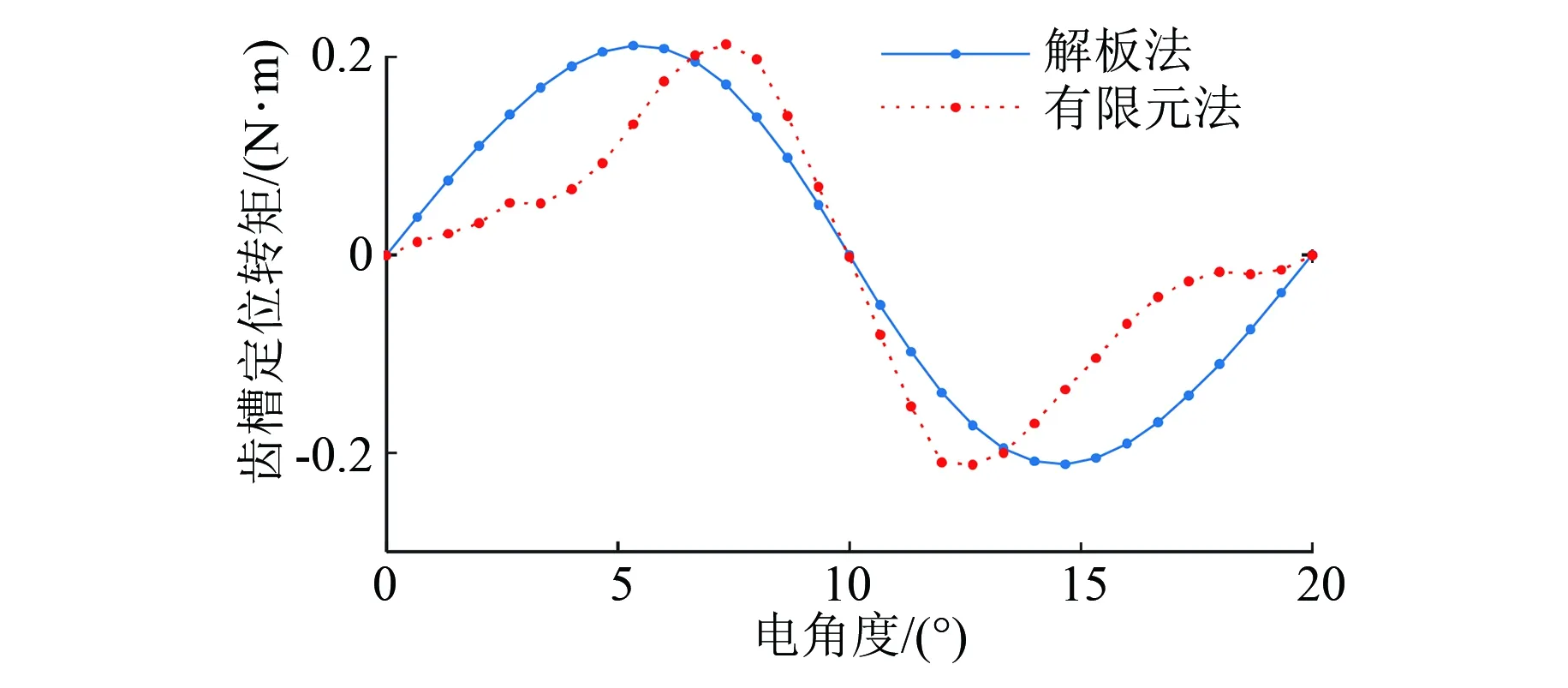
图6 齿槽转矩波形对比

图6中，解析法齿槽转矩峰峰值为0.426 N·m，而有限元法为0.437 N·m，有限元模型计算结果考虑到槽型结构与饱和效应的影响，齿槽转矩波形及最大值出现的位置与解析法计算结果有一定偏差，但整体趋势较为吻合。两者峰峰值误差在3%以内，验证了全域解析法的准确性。

图7是原尺寸电机在额定转速下相空载反电动势的解析法和有限元法计算波形。解析法与有限元法电机转子位置不同，因此2种方法同一相反电动势的相位不同。

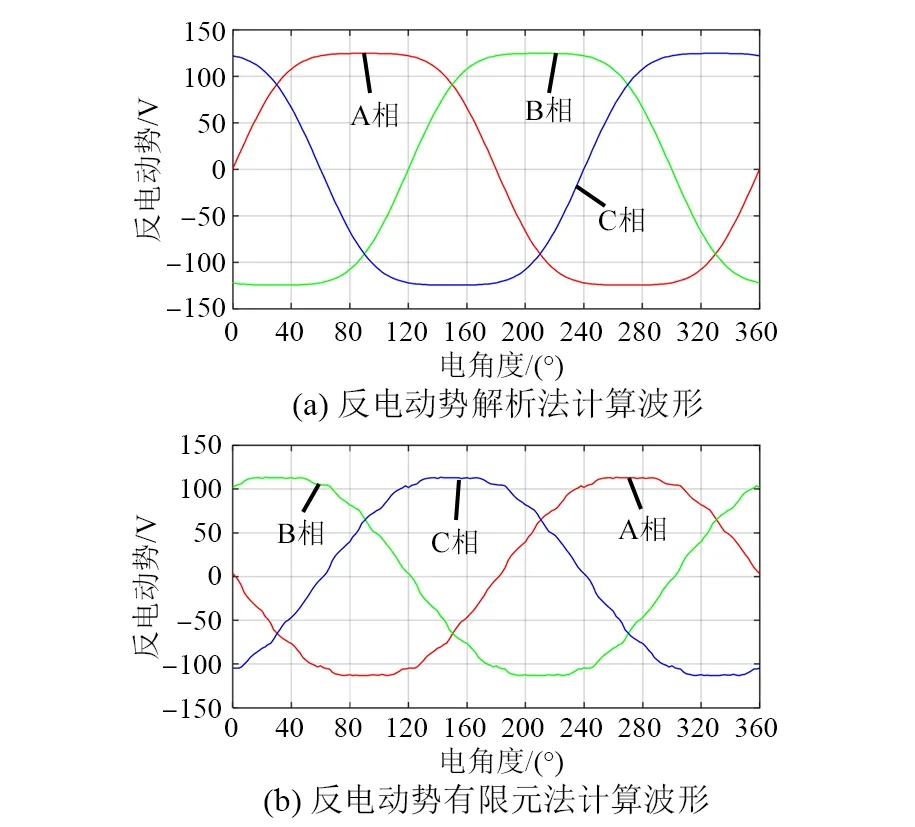
图7 反电动势解析法波形与仿真波形

图7中解析法计算幅值近似为125 V，有限元计算幅值近似为115 V,两者数值误差为8.7%。

由于全域解析法的电机模型不能与有限元仿真电机模型完全相同，如图8所示为有限元仿真模型，计算过程中也采用了一些假设，导致反电动势幅值的解析结果大于有限元结果，但两者波动形状与趋势趋于一致，证明本文的解析模型与方法依然是合理有效的，可以采用该方法进行电机的优化。

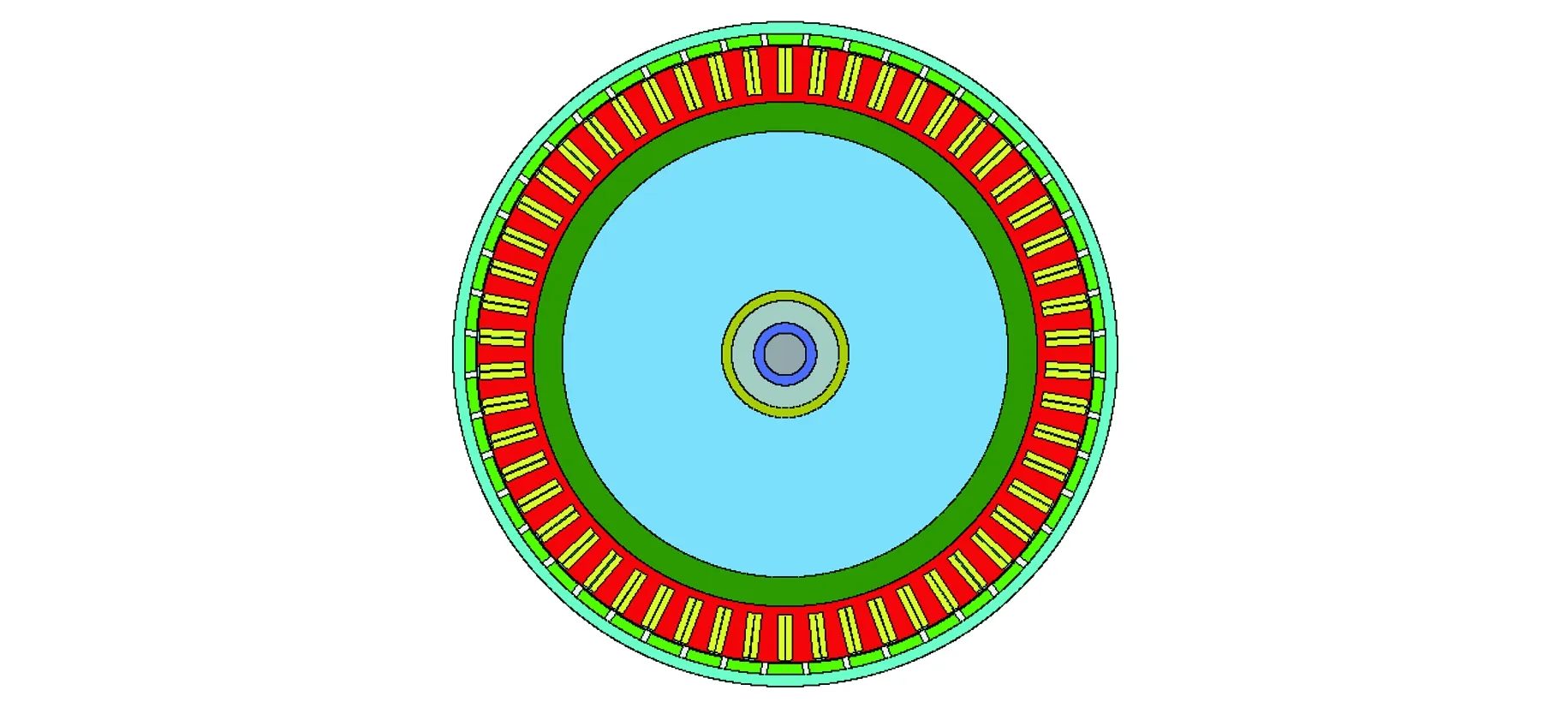
图8 有限元仿真模型

图9是额定电流下电机电磁转矩的解析法和有限元法计算波形。解析法计算转矩平均值为456.8 N·m，有限元计算转矩平均值为455.0 N·m两者数值误差为0.4%。可以看出两种计算方法所得结果较为接近，解析法计算出的平均转矩略大一些。

3.3 基于解析法的多目标优化

通过对比有限元法和解析法的计算结果，验证了解析模型的有效性。本节应用全域解析法对电机多目标、多参数进行优化，以达到电机综合性能的提高。

图10所示为优化后得到的Pareto前沿分布结果。图10(a)为效率、转矩脉动优化结果及其Pareto前沿，可以看出原方案在Pareto前沿包络线内，且优化后的结果优于原方案；图10(b)为效率、永磁体质量优化结果及其Pareto前沿，可以看出原方案在Pareto前沿包络线内，且优化后的结果优于原方案；图10(c)为转矩脉动、永磁体质量优化结果及其Pareto前沿，可以看出原方案在Pareto前沿包络线内，且优化后的结果优于原方案。由于设置了3个优化目标，而选取图10 Pareto前沿中的一个，即可得到3个优化目标的Pareto前沿。这3个Pareto前沿是各兼顾了优化目标其中的2个优化目标。根据Pareto前沿包络线曲率最大的原则设计优化前后方案对比如表3所示。

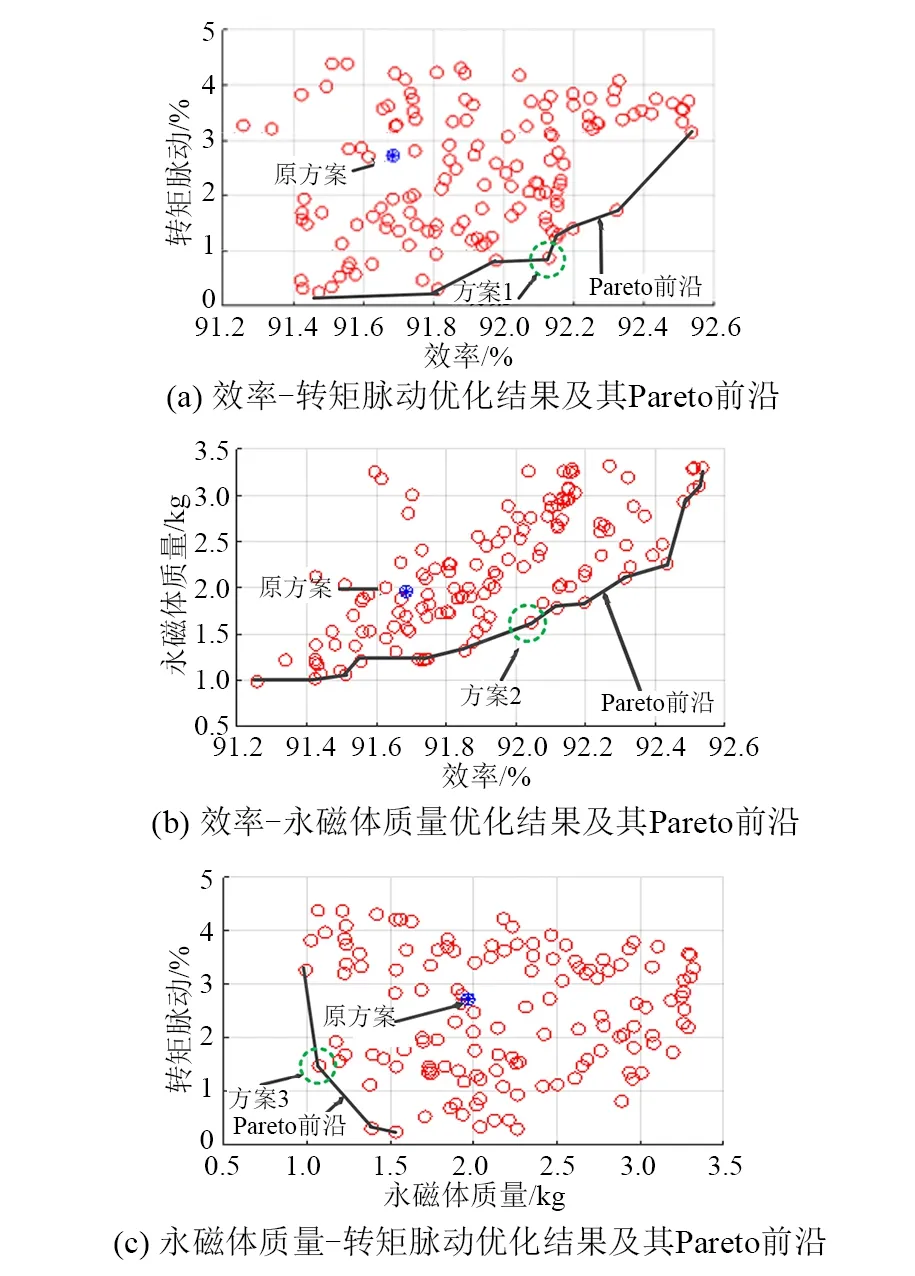
图10 NSGA-Ⅱ 30代优化结果

表3所示为原方案与优化后3个方案的优化目标对比。从表3中可知方案3永磁体用量最少但效率降低，方案2转矩脉动较大，方案1在永磁体质量增加不多的情况下，效率提升了0.45%，转矩脉动下降了一倍。因此，选择方案1为最终确定方案。

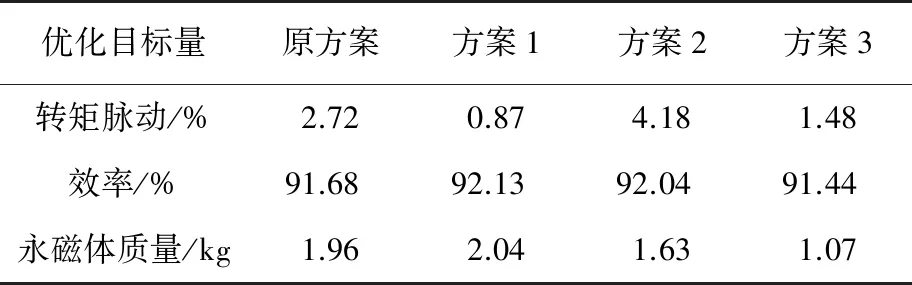
表3 优化前后方案对比

应用有限元法进行多目标优化,与解析法多目标优化设置同样的优化变量、优化目标函数以及限制变量函数。优化30代，每一代父代种群数与子代种群数均为30。

表4所示为有限元法多目标优化与解析法多目标优化时长对比。由表4可知进行多目标优化时，解析法应用时间更短，能大大缩短优化时长。

表4 有限元法多目标优化与解析法多目标优化时长对比

由表4可知应用有限元软件设计优化进行多目标优化时，一旦种群数目、遗传代数增加，计算时长会显著增加，很难满足优化周期的要求，因此应用有限元进行设计时，通常是借助经验掌握各个参数对电机性能的影响规律，然后对每一个参数进行逐个优化，难以兼顾多个目标优化。

应用解析法降低仿真计算时间，结合NSGA-Ⅱ遗传算法对电机实现多目标优化有助于电机参数的极限设计，能够有效地提升电机优化效率，提高电机初步设计的综合性能。

3.4 优化后样机试验验证

本文对优化后样机进行试验验证，采用2台电机对拖运行，被测电机采用转矩控制，陪测电机采用转速控制，系统配备水冷系统如图11所示。图12所示为样机实物图。

图11 试验平台

图12 样机实物图

表5为优化前后样机设计变量值。通过对比可知优化后电机气隙减小，这样能够提升电机的出力，提高电机的效率；通过永磁体极弧系数以及定子槽口张开角度的优化可以降低电机的转矩脉动；增加永磁体厚度可以提高永磁体的磁动势和电机气隙磁密，提升电机出力和效率。

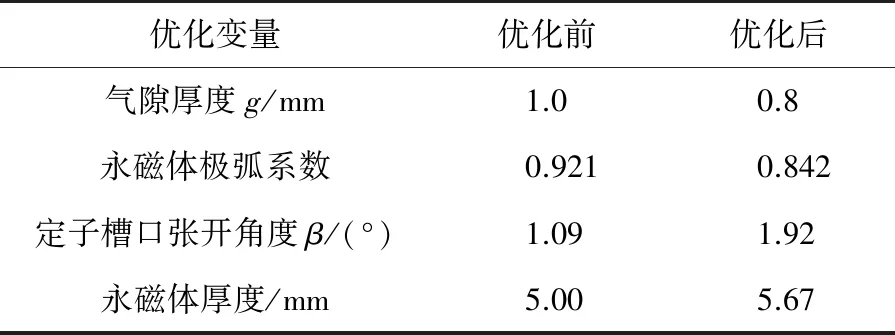
表5 优化前后样机设计变量

表6为450 N·m、600 r/min时样机优化前后效率的试验值和仿真值以及电机永磁体质量实际值和计算值。通过对比可知效率试验值与解析法仿真值吻合较好，验证了解析法的准确性及本文所实施多目标优化方法的有效性。

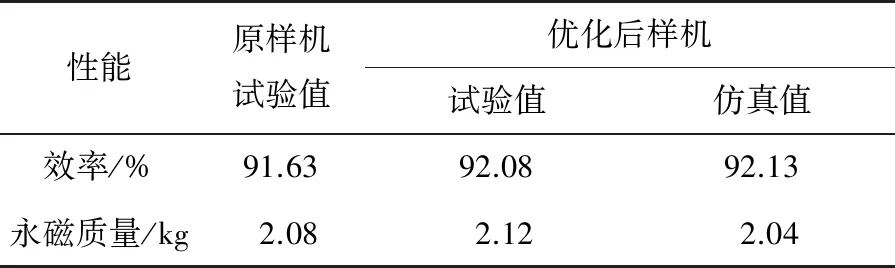
表6 仿真与试验数据比较

4 论 语

(1) 本文应用全域解析法对外转子PMSM进行电磁场求解。通过对比可知，电机齿槽转矩、气隙磁密及反电动势解析计算波形与有限元法计算波形较为吻合，验证了全域解析法对外转子PMSM求解的准确性。

(2) 结合全域解析法求解的快速性，本文应用NSAG-Ⅱ优化算法，对电机性能进行多目标优化。与电机初始方案相比，优化后的电机方案在永磁体质量增加不多的情况下，电机效率提升了0.45%，优化后的电机方案仿真计算所得转矩脉动减小，电机综合性能得到有效提高。

(3) 通过试验及解析计算对比可知,效率的试验值与解析法仿真值吻合较好且在永磁体质量增加不多的情况下样机效率有效提高，验证了解析法的准确性及本文所实施多目标优化方法的有效性。