环形驻波超声波电机定转子接触摩擦模型*
蒋春容, 成苏南, 任香亭, 陆旦宏
(1.南京工程学院 电力工程学院,江苏 南京 211167;2.国网江苏省电力有限公司新沂市供电分公司,江苏 新沂 221400)
0 引 言
超声波电机以其优良的性能在航空航天、医疗设备等领域获得了应用[1-3]。接触摩擦问题一直是超声波电机性能提升中需要解决的关键问题。目前,对行波型超声波电机接触摩擦问题的研究最为常见[4-8]。驻波型超声波电机因其结构设计更为灵活多样而获得了越来越多的关注,各种结构的驻波型超声波电机不断被提出[9-10]。驻波型超声波电机接触摩擦特性与行波型超声波电机有较大的不同。对驻波超声波电机接触摩擦问题的研究,主要以板式弯曲驻波超声波电机[11-12]和纵弯复合驻波超声波电机[13-15]为主。实际上,对不同的驻波型超声波电机,由于驱动足运动轨迹的差异,难以找到一种通用的接触摩擦模型,而要根据驻波型超声波电机自身运动的特点,建立描述其定、转子/动子接触摩擦特性的模型[16]。对采用径向振动的环形驻波超声波电机接触摩擦问题的研究刚起步,其接触摩擦传动机理还有待进一步探索。
在对超声波电机接触摩擦问题的研究中,大多采用库伦摩擦定律建立定转子接触摩擦模型。库伦摩擦定律从最简单的层面描述了摩擦现象。然而,摩擦是复杂的非线性问题,库伦摩擦并不能准确描述摩擦界面的诸多特性,导致计算结果往往存在较大误差[17]。因此,学者们对摩擦问题进行了深入研究,对库伦摩擦进行了改进,提出了包括库伦摩擦+黏性摩擦、Stribeck摩擦、Karnopp摩擦等在内的多种摩擦定律或模型[18]。目前,对采用改进后的摩擦定律或模型建立超声波电机接触摩擦模型的报道较少。
本文针对采用径向振动的环形驻波超声波电机,分析定转子的接触摩擦特性,借助库伦摩擦+黏性摩擦定律,建立定转子接触摩擦模型。基于所建立的模型,分析定转子接触界面上的摩擦力变化情况,以及不同振幅和结构参数对电机转矩-转速特性的影响。最后,测量样机的转矩-转速特性,并将测量值与计算值进行对比,同时也给出基于库伦摩擦定律所建立模型的计算结果,对比结果验证了基于库伦摩擦+黏性摩擦定律所建立模型的准确性。
1 电机结构
环形驻波超声波电机的结构如图1所示,电机定子由压电陶瓷、金属薄圆环和弹性叶片构成。弹性叶片以一定的倾斜角度沿周向布置在金属薄圆环外侧,并与转子内侧接触产生一定的弹性弯曲变形。转子与转轴通过螺钉固定连接。电机采用定子一阶径向伸缩振动作为工作模态,压电陶瓷沿轴向极化,给压电陶瓷通以特定频率的单相交流电,激发出定子的一阶径向伸缩振动,即径向驻波振动。弹性叶片根部在金属薄圆环的带动下沿径向往复运动。同时,弹性叶片也起到定转子间弹性耦合器的作用,将根部的径向运动传递到与转子接触的端部,并在接触过程中将径向运动转化为沿转子切向的往复运动,从而推动转子旋转。
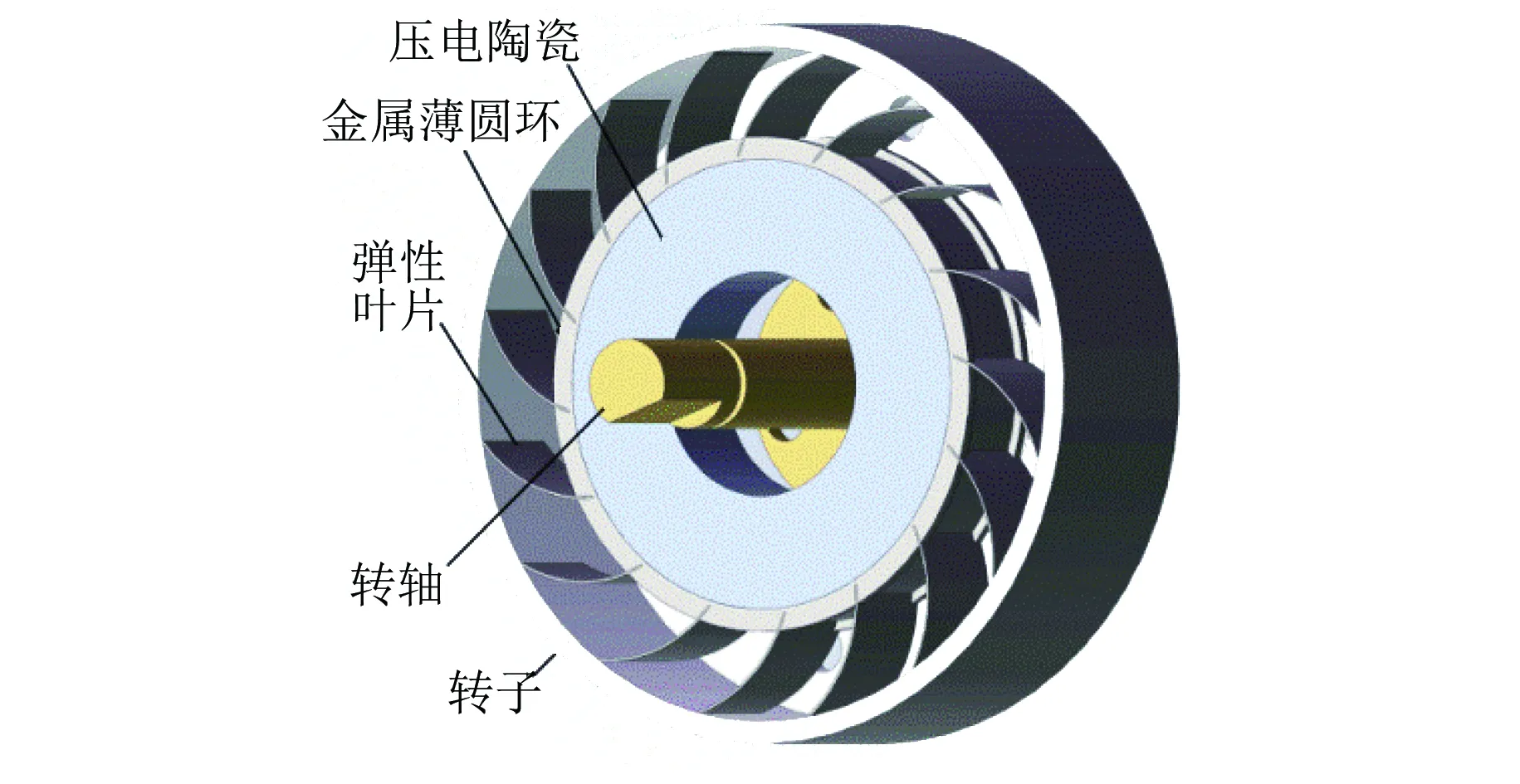
图1 电机结构示意图
2 定转子接触摩擦模型
考虑到接触摩擦问题的复杂性,为简化分析,模型采用如下简化假设:
(1) 电机工作在稳定运行状态;
(2) 忽略轴承的摩擦损耗;
(3) 忽略叶片加工和安装过程中引起的叶片工作状态不对称,认为各叶片工作状态均一致。
2.1 定子的振动
定子的工作模态为一阶径向伸缩振动,考虑到结构的对称性和运动的一致性,在分析定转子的接触摩擦特性时,可以取一个弹性叶片为代表进行分析,如图2所示。弹性叶片安装到金属薄圆环外侧时与定子径向保持β的倾斜角,与转子组装好后,弹性叶片产生弹性弯曲变形,其形状为弧线AB,由于弯曲变形量较小,分析时把弧线AB近似用直线AB代替。直线AB与弹性叶片未发生弯曲变形时所在位置的夹角为φ。直线BO与直线BA的夹角为α。定子的振动为微米级,而电机的结构参数为毫米级,因此可以忽略定子振动引起的φ和α夹角的变化,认为这两个夹角仅由电机的结构参数决定。设弹性叶片AB的长度为l,金属薄圆环的外半径OA长度为r1,转子的内半径OB长度为r2,则可求得φ和α的大小分别为
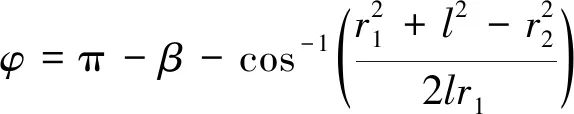
(1)
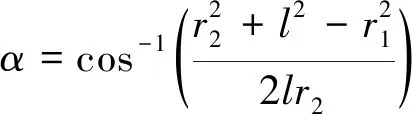
(2)
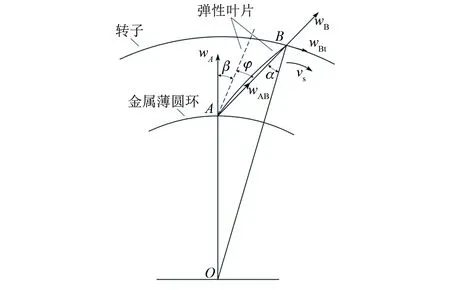
图2 定转子的接触
定子金属薄圆环表面A点的径向振动位移可表示为
wA=Wsin(ωt)
(3)
式中:W为定子径向振动的振幅;ω为振动的角频率。
A点沿AB方向的位移分量为
wAB=Wcos(β+φ)sin(ωt)
(4)
A点的振动沿弹性叶片传递到端部的B点,因此,图2中,B点的位移wB=wAB。弹性叶片端部B点沿转子切向的位移分量为
wBt=Wcos(β+φ)sin(α)sin(ωt)
(5)
将位移对时间求导数,即可得到弹性叶片端部B点的切向速度vs为
vs=vsmcos(ωt)
(6)
式中:vsm为切向速度幅值,vsm=Wωcos(β+φ)·sin(α)。
在电机正常工作时,弹性叶片与转子始终处于接触状态,弹性叶片端部B点与转子不分离。
2.2 定转子的接触摩擦传动
设转子内径处的旋转线速度为vr,则弹性叶片顶端B点与转子的相对速度为
vrel=vs-vr
(7)
当vrel>0时,弹性叶片推动转子旋转;当vrel<0时,弹性叶片阻碍转子旋转。
当弹性叶片推动转子旋转时,如图3所示,弹性叶片顶端B点受到来自转子的作用力,包括沿转子法向的压力Fn1和沿转子切向的摩擦力Ftdrive,Ftdrive的方向与转子旋转方向相反。将Fn1和Ftdrive沿弹性叶片AB法向和切向两个方向分解可以得到Fq1和Fp1,并有如下关系:
Fq1=Fn1cos(α)+Ftdrivesin(α)
(8)
Fp1=Fn1sin(α)-Ftdrivecos(α)
(9)
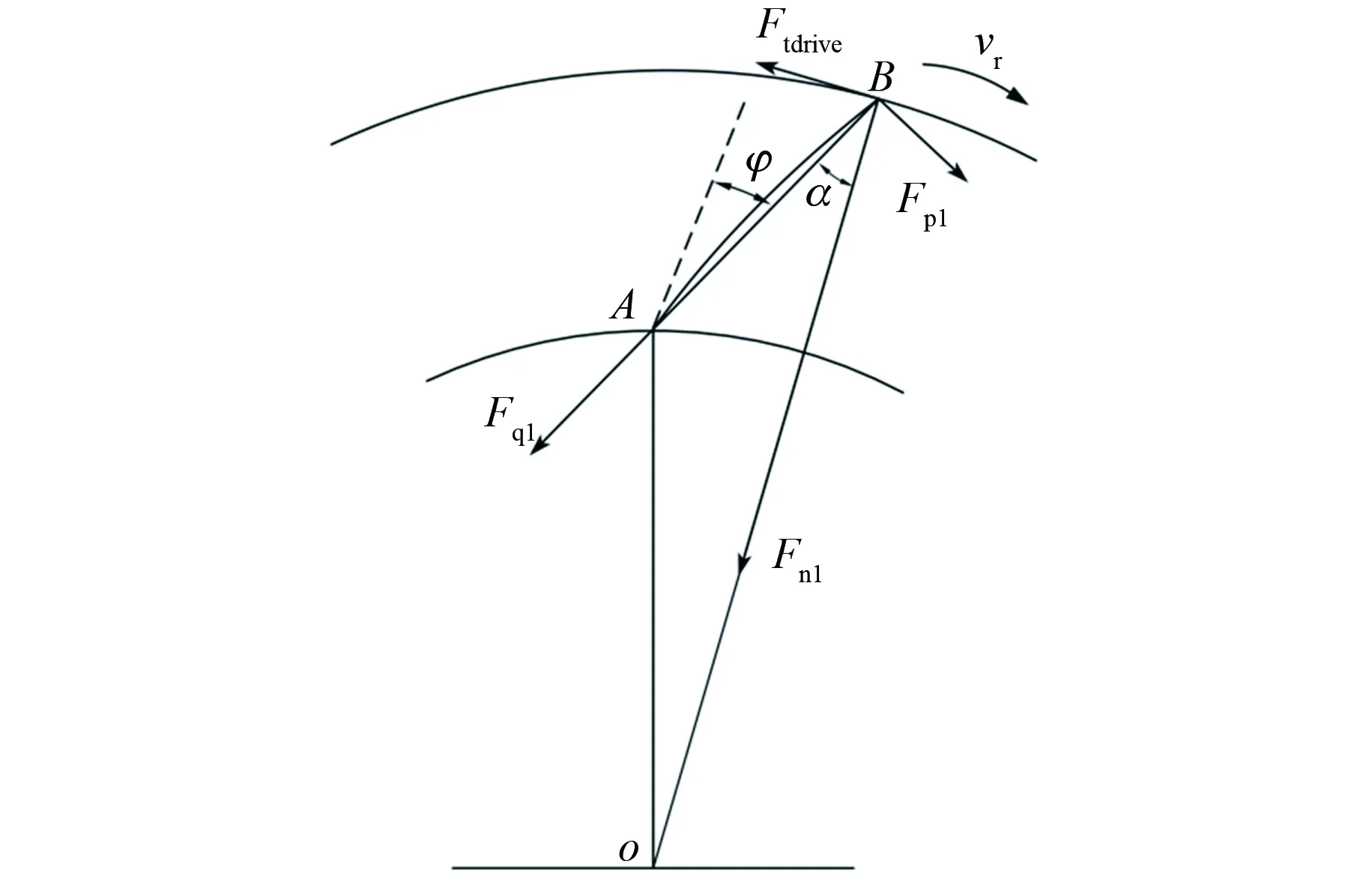
图3 定子推动转子旋转时的受力分析
根据库伦摩擦+黏性摩擦定律[18],转子作用在弹性叶片顶端B点的法向压力Fn1与切向摩擦力Ftdrive之间满足:
Ftdrive=μdFn1+fvvrel
(10)
式中:μd为动摩擦系数;fv为黏性摩擦系数。
当fv取值为0时,库伦摩擦+黏性摩擦定律就退化为库伦摩擦定律。联合求解式(9)和式(10)可以得到弹性叶片对转子的推力:
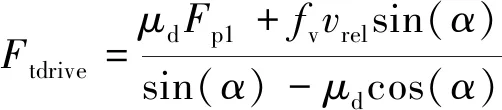
(11)
通过式(11)求Ftdrive,还需要知道Fp1的值。Fp1是弹性叶片推动转子旋转过程中维持弹性叶片弯曲变形的作用力。因为定子振动的幅度比电机的结构尺寸要小得多,所以可忽略定子振动引起的弹性叶片弯曲变形量的变化,认为其弯曲变形量保持不变。根据弹性叶片的弯曲变形量可以求得:
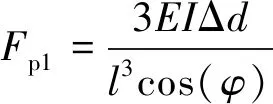
(12)
式中:E为弹性叶片的弹性模量;I为弹性叶片的截面惯性矩;Δd为弹性叶片端点的挠度。
Δd可表示为
Δd=lsin(φ)
(13)
由式(12)求得Fp1的值后代入式(11),即可求得弹性叶片推动转子旋转的摩擦力。
当弹性叶片阻碍转子旋转时,如图4所示,弹性叶片顶端B点受到来自转子的作用力,包括沿转子法向的压力Fn2和沿转子切向的摩擦力Ftbrake,Ftbrake的方向与转子旋转方向相同。同理,将Fn2和Ftbrake沿弹性叶片AB法向和切向两个方向分解可以得到Fq2和Fp2,并有如下关系:
Fq2=Fn2cos(α)-Ftbrakesin(α)
(14)
Fp2=Fn2sin(α)+Ftbrakecos(α)
(15)
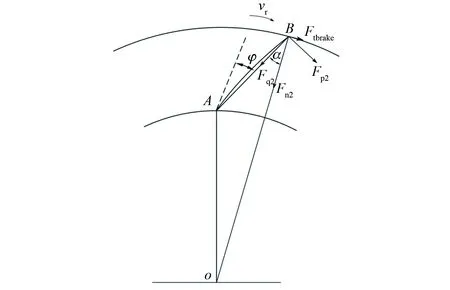
图4 定子阻碍转子旋转时的受力分析
转子作用在弹性叶片顶端的法向压力Fn2与切向摩擦力Ftbrake之间满足:
Ftbrake=μdFn2-fvvrel
(16)
联合求解式(15)和式(16)可得:
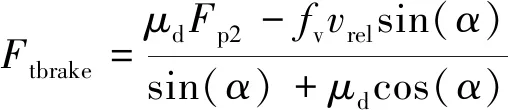
(17)
式中:Fp2为弹性叶片阻碍转子旋转过程中维持弹性叶片弯曲变形的作用力。
忽略定子振动对弹性叶片弯曲变形量的影响,弹性叶片在阻碍转子旋转时的弯曲变形量与推动转子旋转时的弯曲变形量一致,因此有Fp2=Fp1。
由式(11)和式(17)可分别求得弹性叶片推动和阻碍转子旋转的摩擦力大小。电机运行到稳态时,一个周期T内弹性叶片端点的切向速度vs与转子旋转线速度vr的相对关系如图5所示,图5中,t1和t4是二者速度相等的时刻点,t2和t3是弹性叶片端点切向速度过零的时刻点。根据速度相等可求得t1和t4的值分别为
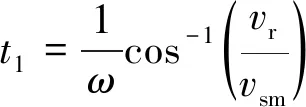
(18)
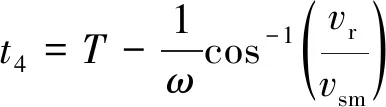
(19)
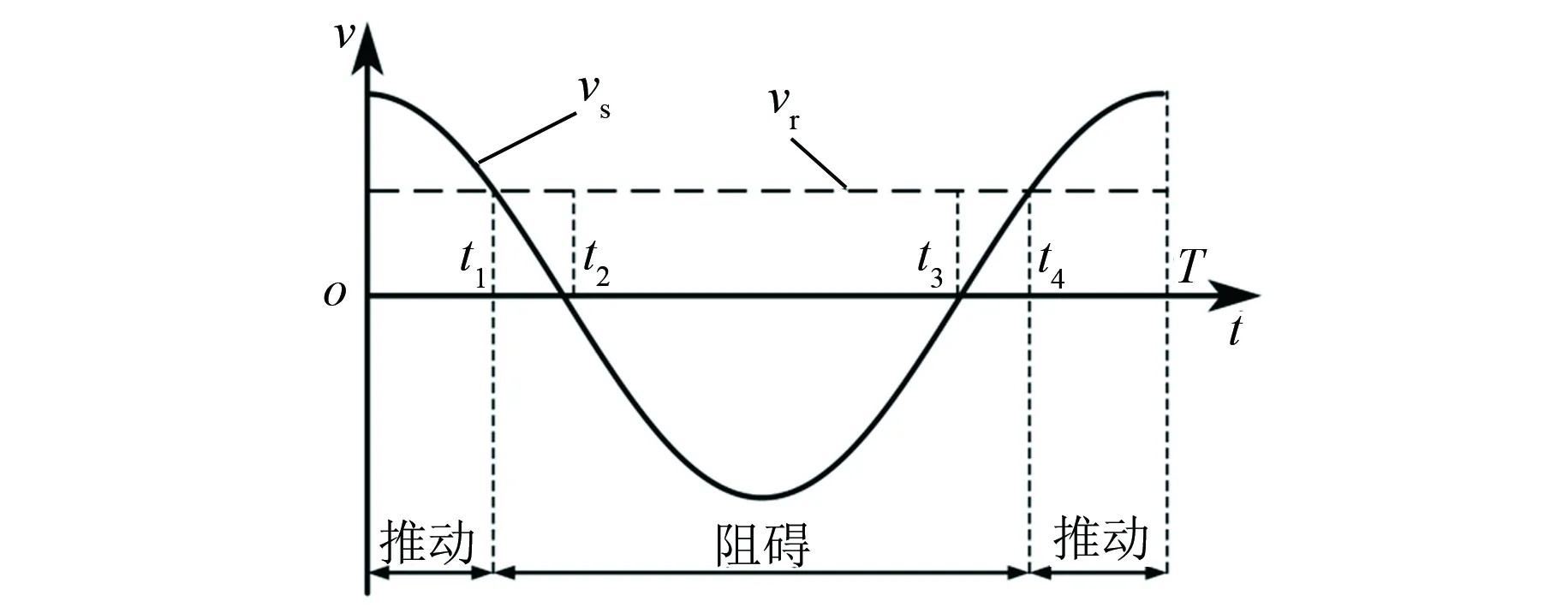
图5 定转子的相对速度
在0~t1时间段以及t4~T时间段,弹性叶片端部的速度高于转子的速度,弹性叶片以Ftdrive的摩擦力推动转子旋转。在t1~t4时间段,弹性叶片端部与转子之间的相对速度小于零,弹性叶片以Ftbrake的摩擦力阻碍转子旋转。一个周期内,弹性叶片对转子的切向摩擦力可表示为
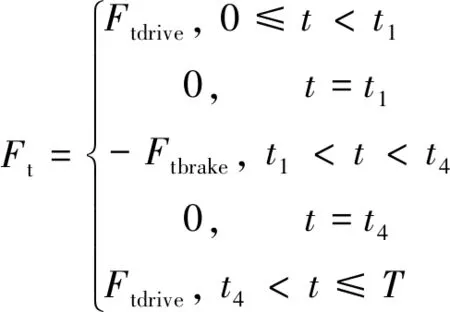
(20)
一个周期内弹性叶片对转子的平均推力为
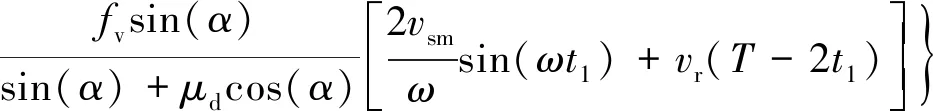
(21)
弹性叶片对转子的推动力矩,也即负载转矩,可由平均推力计算得到:
TL=Favgnr2
(22)
式中:TL为负载转矩;n为弹性叶片的数量。
3 计算结果及分析
根据建立的定转子接触摩擦模型,对样机进行计算。样机参数如表1所示。样机定子工作模态的共振频率为73.3 kHz。正常工作时施加正弦交流电压,其驱动频率f为74 kHz,当电压幅值为100 V时,用激光测振仪测得定子的径向振幅为0.6 μm。黏性摩擦系数fv的值难以直接测得,因此通过测量电机的一组转矩转速值,然后利用测得的转矩转速值反求出fv的值。具体步骤为,给电机通以频率为74 kHz、幅值为100 V的正弦交流电,测得电机在堵转时的转矩为0.395 N·m,将测得的转矩值代入式(22)求得平均推动力Favg,再将Favg的值代入式(21)并取vr=0,t1=π/(2ω),求解得到fv的值为2.0。
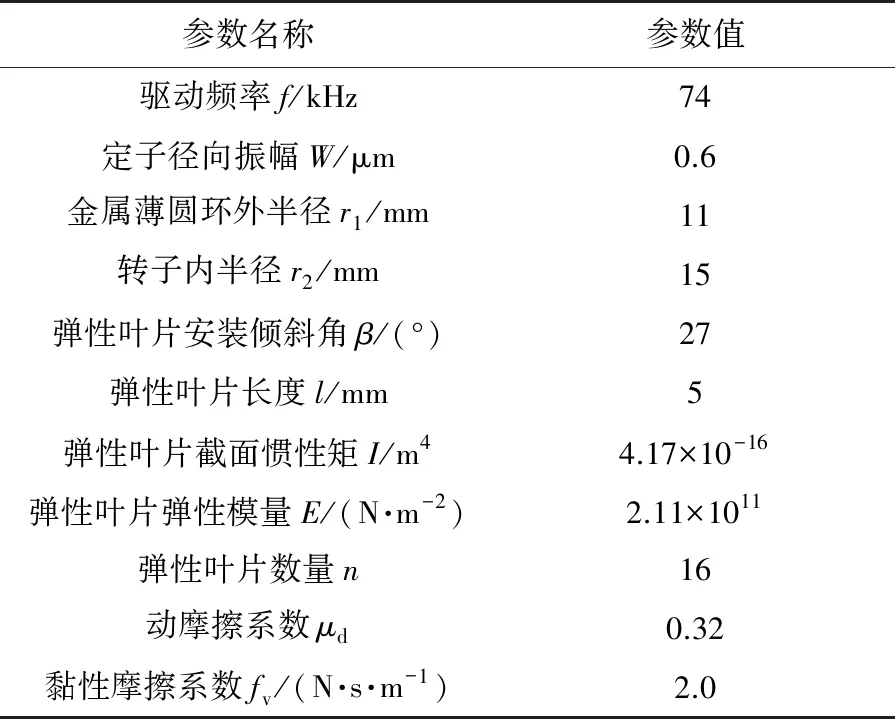
表1 样机参数
根据表1的参数计算一个周期T内电机定转子接触界面摩擦力的变化情况。选取了电机堵转(转速为0 r/min)、轻载(转速为30 r/min)、空载(空载转速为46.8 r/min)三种情况分别计算摩擦力的变化,结果如图6所示。
当电机堵转时,定转子间的摩擦力变化如图6(a)所示。从0~t1时刻,弹性叶片端部的速度vs高于转子转速vr,弹性叶片推动转子旋转,在这个过程中,vs逐渐减小到0,相对速度vrel也逐渐减小,弹性叶片对转子的推动力也逐渐下降。从t1~t4时刻,弹性叶片端部的速度反向,弹性叶片阻碍转子旋转,在这个时间段内,相对速度vrel的大小先是增大而后减小,弹性叶片对转子的阻碍力也随之先略有增大而后稍有减小。从t4~T时刻,弹性叶片端部的速度再次反向,弹性叶片推动转子旋转,相对速度vrel逐渐增大,弹性叶片对转子的推动力也随之逐渐增大。在一个周期内,弹性叶片对转子推动作用和阻碍作用的时间各占一半。根据式(21)和式(22)可求得堵转力矩为0.395 N·m。
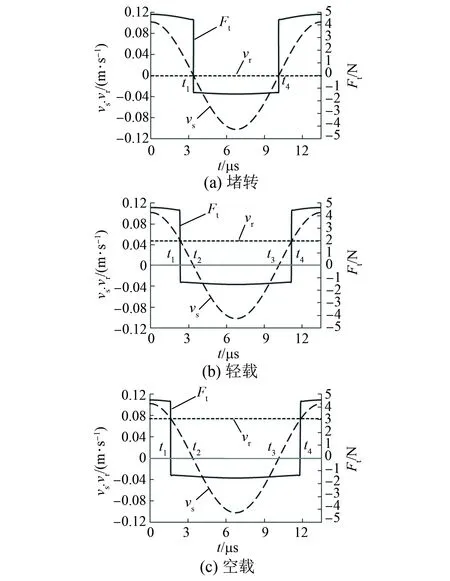
图6 定转子接触界面的摩擦力
当电机轻载时,定转子间的摩擦力变化如图6(b)所示。从0~t1时刻,弹性叶片与转子同方向运动且速度高于转子,弹性叶片推动转子旋转,推动力随着相对速度减小而降低。从t1~t2时刻,弹性叶片仍与转子同方向运动但速度低于转子,弹性叶片阻碍转子旋转。从t2~t3时刻,弹性叶片运动方向与转子相反,弹性叶片阻碍转子旋转。从t3~t4时刻,弹性叶片又变为与转子同方向运动但速度仍低于转子转速,弹性叶片仍阻碍转子旋转。从t1~t4时间段内,相对速度vrel的大小先是增大而后减小,弹性叶片对转子的阻碍力也随之先略有增大而后稍有减小。从t4~T时刻,弹性叶片保持与转子同方向运动且速度高于转子,弹性叶片又转为推动转子旋转,推动力随弹性叶片速度的增加而逐渐上升。可求得转速为30 r/min时对应的负载转矩为0.156 N·m。
当电机转子空载时,定转子间的摩擦力变化如图6(c)所示,此时接触界面摩擦力的变化规律与转子轻载时相似,只不过弹性叶片对转子推动作用的时间更短,阻碍作用的时间更长,一个周期内,弹性叶片对转子的平均推力为零。
定子的径向振幅对电机的输出性能有重要影响。可以通过调整驱动电压的大小以调整定子的径向振幅,进而调整电机的输出性能。利用所提出的模型,以表1的参数作为基准,改变径向振幅大小,分析电机转矩-转速特性的变化情况,如图7所示。转子的转速N可由转子旋转的线速度vr计算得到:N=60vr/(2πr2)。由图7可见,随着定子径向振幅的下降,电机空载转速明显降低,堵转转矩也略有减小,电机输出性能下降。
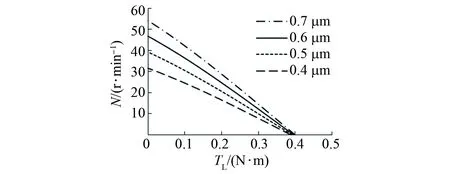
图7 不同径向振幅时电机的转矩-转速特性
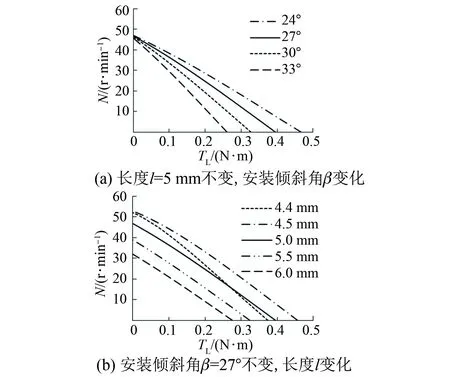
图8 弹性叶片对电机转矩-转速特性的影响
定子弹性叶片的布置方式和结构尺寸会影响电机的输出性能。基于所建立的模型,以表1的参数为基准,分别改变弹性叶片的安装倾斜角β和弹性叶片的长度l,分析电机转矩-转速特性的变化,如图8所示。当弹性叶片的长度l保持5 mm不变,安装倾斜角β从24°增加到33°时,电机转矩-转速特性变化情况如图8(a)所示。随着安装倾斜角变大,电机的堵转转矩明显下降,空载转速略有降低,输出性能总体变差。计算结果表明,当弹性叶片的安装倾斜角超过44°时,弹性叶片不再与转子接触,也即无法推动转子旋转。因此,弹性叶片的安装倾斜角不能超过44°。为了提高电机的输出性能,在保证叶片弹性变形的前提下,应采用较小的安装倾斜角。再分析弹性叶片长度l变化的影响。保持弹性叶片的安装倾斜角β为27°不变,改变弹性叶片长度l,电机的转矩-转速特性变化如图8(b)所示。当l从4.4 mm增加到6.0 mm时,电机的空载转速和堵转转矩均是先增大而后逐渐减小,弹性叶片长度l为4.5 mm时电机的性能为最佳。需要注意的是,当弹性叶片长度小于4.3 mm时,弹性叶片不再与转子接触,也就起不到推动作用。
4 试验验证
为了验证所提出的模型,测量了电机的转矩-转速特性并与理论计算值进行对比,测试平台如图9所示。测量时,由信号发生器产生正弦交流信号经过功率放大器放大后,提供给电机作为驱动电源。考虑到电机低速大转矩特性以及负载转矩调节的便利性,采用磁滞制动器作为负载,负载由直流电源供电并调整大小。电机的转矩和转速值则由转矩转速传感器测量得到。

图9 转矩-转速特性测试平台
在测量转矩-转速特性前,先采用激光测振仪测量了定子在不同电压下的径向振幅,以便能够采用所提出的模型计算对应的转矩和转速值,并能够确定在转矩-转速特性测试过程中施加的电压。激光测振仪测量结果显示:当驱动电压幅值为100 V、频率为74 kHz时,定子径向振幅为0.6 μm;当驱动电压幅值维持100 V不变、频率为74.5 kHz时,定子径向振幅为0.5 μm。测量转矩-转速特性时,分别施加以上两组电压,测量得到对应的转矩-转速特性,并采用所提出的模型进行计算。为了进行对比,同时给出基于库伦摩擦定律所建立模型的计算值,计算时只要取黏性摩擦系数fv的值为0即可。测量值和计算值对比如图10所示。由图10可见,基于库伦摩擦+黏性摩擦定律所建立模型的计算值与测量值能够较好地吻合,说明了所建立模型的准确性。对比两种模型的计算值与测量值的差异,可以发现,基于库伦摩擦+黏性摩擦定律所建立的模型,其计算值能更好地贴近测量值。
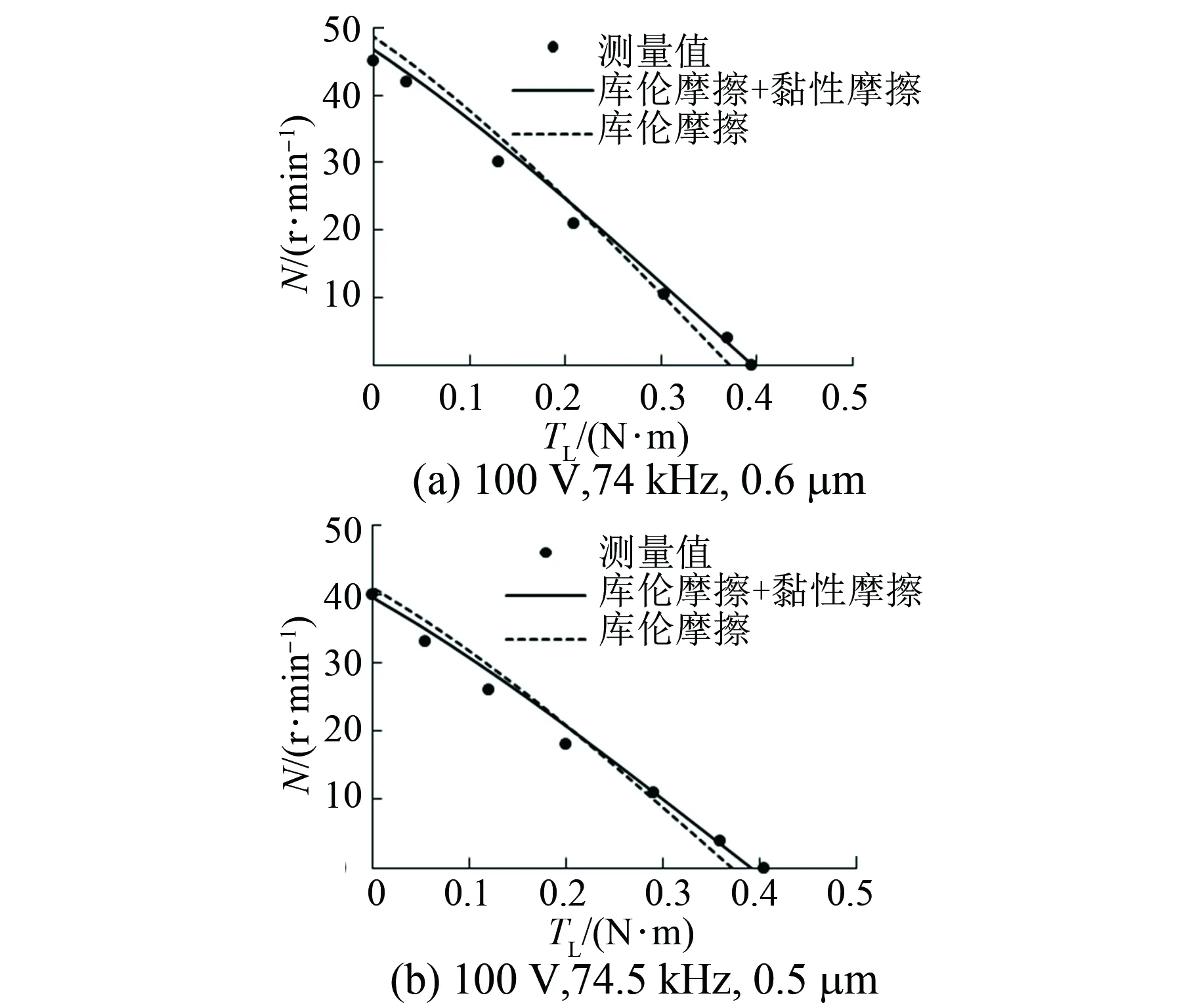
图10 测量值与计算值对比
为了更直观地展示两种模型计算值与测量值对比的结果,给出转速计算值与测量值的均方根误差ΔN的对比。将测量得到的转矩作为两种模型的给定量,求出对应的转速计算值,进而计算转速的均方根误差ΔN:
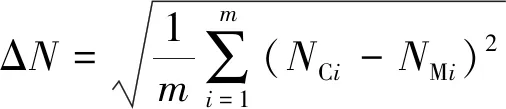
(23)
式中:m为试验测量的数据点数;NCi和NMi分别为第i个转速的计算值和测量值。
两种模型的转速均方根误差ΔN的对比如表2所示。由表2可见,与采用库伦摩擦定律所建立的模型相比,采用库伦摩擦+黏性摩擦定律所建立模型的计算结果误差更小。其改进的原因在于,库伦摩擦定律简单地认为切向摩擦力与法向压力成正比,而库伦摩擦+黏性摩擦定律不仅考虑了切向摩擦力与法向压力之间的关系,而且反映了定转子间的相对运动速度对切向摩擦力的影响,从而使所建立的模型能更准确地描述接触界面的摩擦传动特性。

表2 两种模型的转速均方根误差对比
5 结 语
本文分析了环形驻波超声波电机定转子的接触以及摩擦传动特性,采用库伦摩擦+黏性摩擦定律建立了定转子接触摩擦模型。基于所建立的模型,分析了定转子接触界面摩擦力的变化情况,计算了定子不同径向振幅以及弹性叶片安装方式变化对电机的转矩-转速特性的影响。最后,搭建试验测试平台测量了电机的转矩-转速特性,并将测量结果与计算结果进行对比,二者相吻合,验证了所建立的模型。同时也对比了基于库伦摩擦定律所建立模型的计算值,结果显示,与采用库伦摩擦定律相比,采用库伦摩擦+黏性摩擦定律所建立模型的计算值能更好地贴近测量值,说明采用库伦摩擦+黏性摩擦定律所建立的模型能更准确地描述电机定转子接触界面的摩擦传动特性。

