基于刀具摆角的内螺纹铣削干涉建模与应用

张祥兵，张 恒，于选坤，方丽萍，杨 浩

（上海飞机制造有限公司 上海 201324）

0 引言

民用飞机上有多种结构整体化零件，如整体壁板、转轴接头和应急门框等，可以起到减轻飞机重量的作用。该类零件具有薄壁、深腔、镂空、精孔、内螺纹等多种构型，往往需要在五坐标机床上多次加工完成。其中，内螺纹一般需满足3B级精度，对数控铣削内螺纹加工方法有较高要求。

螺纹加工方法有切削、磨削、电火花和成型加工等多种[1]。螺纹铣削是切削加工中的一种，其他切削方法还有车、镗、旋风铣等等。螺纹铣削原理为：成型刀具在数控铣床上进行XY轴圆弧插补的同时，Z轴完成直线插补，即刀具按螺旋轨迹进刀，形成螺旋切削面[2]。具有安全可靠、应用范围广、易加工超级合金等特点[3～6]，在航空航天、核电、医疗器械、模具制造等领域受到广泛应用。

铣削螺纹面与理想螺纹之面间会存在几何偏离，可以称为干涉或误差。Guillaume等人1,7～10给出可通过改变刀具位置或调整刀具轮廓两种方法来减少误差，本文在分析干涉生产的模型上提出一种改变刀具轴线的方法减少干涉。由于外部螺纹铣削产生的干涉较少[11]，本文主要集中到内螺纹上的研究上，以UNJ型为分析对象，其他类型的内螺纹也可以参考文中方法进行分析。

1 刀轴摆角铣削干涉建模

1.1 定义坐标系

文献[1]描述了三轴联动加工过程中，螺纹铣刀与螺纹面之间会出现干涉。在螺纹刀具尺寸确定的情况下，需迭代优化螺旋轨迹直径。由于干涉源于螺旋升角与刀具角度之间的偏差，本文提出在切削过程中时刻让刀具轮廓倾斜一个角度，使刀具轮廓平行于或近似平行于理想螺纹面，减少螺纹切削干涉。

建立工件与刀具坐标系如图1所示，其中OXYZ为工件坐标系，为刀具坐标系。绕OZ轴做旋转运动，经一段时间（逆时针旋转角度α），到达初始位置如图1所示。

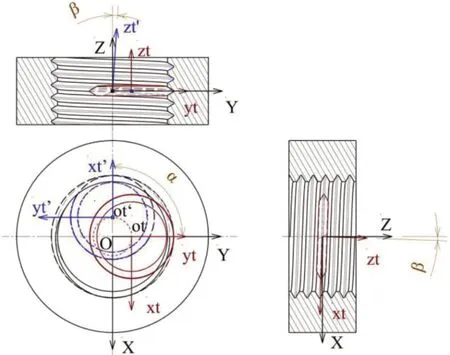
图1 工件与刀具坐标系

刀具轴线方向向量可表示为(sinβ·cosα,sinβ·sinα,cosβ)，刀具轴线可以表示为：

1.2 内螺纹轮廓建模

航空用螺纹具有配合精度高、使用寿命长等特点，广泛应用于各种航空零部件。根据AS8879-2004标准，螺纹轮廓如图2所示。

图2 标准UNJ型内螺纹轮廓

最大材料状态螺纹轮廓：

中径：基本中径D2，也是最小螺纹中径，D2=D-3H/4；

大径：基本大径D，也是最小螺纹大径（即公称直径）；

小径：基本小径D1，也是最小小径，D1=D-9H/8；

牙底：牙底圆弧Rroot=，对应内角120°，最大尺寸D+Rroot；

最小材料状态螺纹轮廓：

中径：中径D2m，最大中径，D2m=D2+TD2,其中TD2中径公差；

大径：大径Dm，最大大径，

小径：小径D1m，最大小径，D1m=D1+TD1其中TD1小径公差；

在最大材料状态下，使用6个节点描述最小螺纹轮廓（理想螺纹轮廓），其中Kt=1/8。

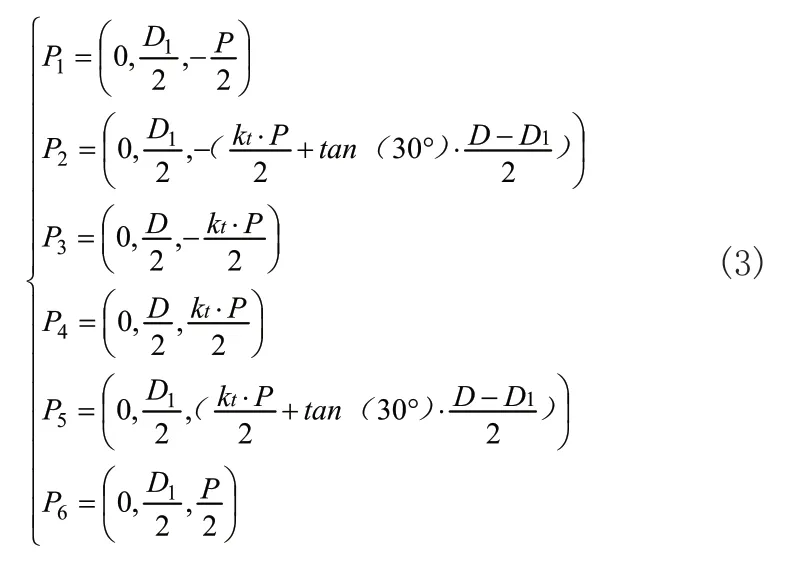
最小轮廓线可以表述如下；

在最小材料状态下，使用6个节点描述最大螺纹轮廓，其中Kt=1/24；

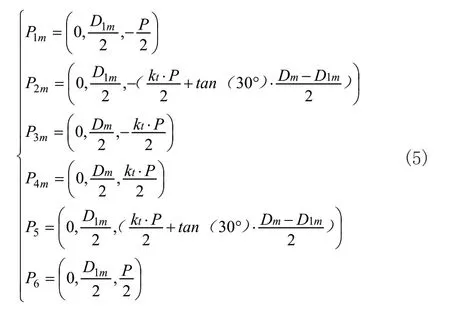
最大轮廓线可以表述如下；

1.3 理想内螺纹面建模

可以由轮廓线(4)上任意点Pi环绕形成的螺旋线组成最小螺纹面，即理想螺纹面，在极坐标下，理想螺纹面可以由下式表达：

式(5)中，右旋螺纹取正号，左旋螺纹取负号。0.5-20UNJF-3B的螺纹面可以由MATLAB软件计算得到，如图3所示。

图3 0.5-20UNJF-3B最大材料轮廓(黄色)及最少材料轮廓(红色)

同理，可以由轮廓线(6)上任意点Pi环绕形成的螺旋线组成最大螺纹面，即实际螺纹的最大极限位置。

1.4 螺纹铣刀轮廓建模

图4 螺纹铣刀轮廓模型

在ot xtytzt坐标系内，刀具尺寸可以有交点及圆角换算得到：

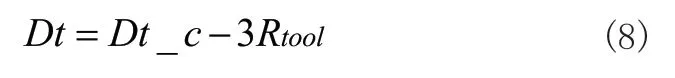
为了方便描述，可以用四个点描述螺纹铣刀轮廓；

在ot xtytzt坐标系内，螺纹铣刀轮廓线可以表示为：

1.5 铣削螺纹面建模

在OXYZ工件坐标系内，某瞬时α，螺纹铣刀表面上任意点Pstool(xt,yt,zt)∈Stool，满足：

式(11)中，右旋螺纹取正号，左旋螺纹取负号，α为公转角度，θ为自转角度，β为刀具摆角。当α由0变化N*360°时，刀具绕OZ轴旋转N圈形成的铣削螺纹面。

取Dt=9.82的螺纹铣刀，加工0.5-20UNJF-3B螺纹。当β取0，即刀具不摆角，每个切削瞬时，刀具与理想螺纹表面之间有干涉，如图5(b)网格区域所示；一个螺距内，理想螺纹表面包裹于刀具切削形成面之内，如图5(a)网格区域所示。

当β取1.95°，即刀具摆角1.95°。刀具外形与理想螺纹面之间形成干涉大幅减少，如图5(b)斜线区域所示。

图5 Dt=9.82的螺纹铣刀加工0.5-20UNJF-3B螺纹干涉模拟

1.6 干涉建模

铣削螺纹面与理想螺纹面之间的干涉具有轴对称特点，为了便于分析，在OXYZ坐标系内取YOZ进行讨论。螺纹铣刀表面上任意点Pstool(xt,yt,zt)∈Stool,在YOZ平面产生的干涉应满足：当α由0变至360°时，x=0，且式(11)成立。

图6绘出了刀具上一切削点（P3t、P4t的中点），在刀具绕工件轴线旋转时，对理想螺纹轮廓的影响。图中蓝色曲线为β取0°时轨迹线，红色曲线为β取1.95°时的轨迹线。从图6中可知，切削轨迹线影响螺纹加工精度，刀具摆角可以降低铣削螺纹轮廓误差。

图6 刀具上轮廓中位切削点对螺纹截面的影响

进一步对该误差进行建模。轨迹线Lp t i上某点(0,y,z)在理论轮廓左侧，则该点包容于理想螺纹面；若该点在理论轮廓右侧，则该点过切与理想螺纹面。误差可以表示为：

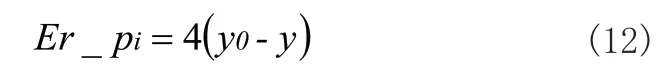
其中Er_pi为正值表示残留，Er_pi为负值表示过切，(0,y0,z0)为理论轮廓线上的一点。轨迹线Lpti上误差最大的一点(0,ym,zm)满足：

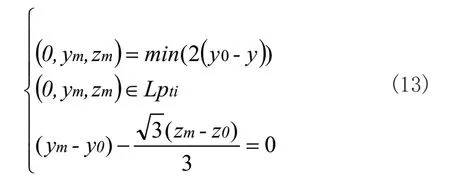
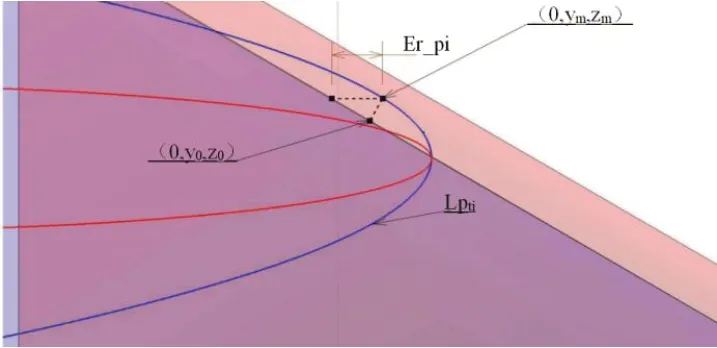
图7 刀具上某切削点对理想螺纹轮廓的误差

2 仿真与应用

2.1 基于matlab仿真结果

在YOZ平面内轮廓线上拾取若干点位，分别计算各点位上的最大偏差。经MATLAB数值计算，结果如图8所示。可以判断，所有最大偏差点的总和也就是铣削螺纹面。

图8 刀具切削点轨迹对理想螺纹轮廓的影响

从图8可以看出，螺纹轮廓上各点误差一致性高，非摆角状态下误差变化为1.5μm，摆角状态下误差变化为0.66μm，同时还可以看出增加一定的刀具摆角可以大幅减小各点误差。

通过对比不同摆角β的变化来分析轮廓上任意点误差的变化，得到摆角β的最优取值。数值计算结果，如图9所示。在非摆角状态下，加工误差受刀具直径、螺距等因素影响。相同公称直径下，螺距越大，非摆角状态下加工误差越大；在相同公称直径和螺距下，螺纹铣刀直径越大加工误差越大。

图9 摆角-加工误差计算结果

在摆角状态下，可以减小加工误差；当摆角选取为某一特定角度，可以将误差控制在0.5μm以内。该摆角产生的误差与摆动中径升角λ产生的误差相差不大。

为了计算方便，可令摆角β=λ，计算的结果如表1所示，可满足工程应用。

表1 不同刀具直径切削产生的加工误差

中径处螺纹升角可通过如下公式计算：

1）对牙侧角的影响由于加工误差的存在，螺纹中径随之增加，但由于轮廓面上每点的误差变化较小，螺纹轮螺角度变化可以忽略不计。

2）对螺纹大径的影响轨迹线Lpti为铣刀轮廓上某切削点在螺旋上升过程中与YOZ面交点的集合，轨迹线Lpti任意点的y坐标均不大于对应轮廓点的y坐标，因此摆角对螺纹大径无影响。模拟结果如图10所示。

图10 非摆角（蓝色）与摆角（红色）状态下的包络轮廓

3）对螺纹牙底的影响对螺纹底角的影响可以归纳为式(15)，因此刀轴摆角可以减少干涉对螺纹牙底的影响。

2.2 基于CATIA编程实切

在CATIA内编程模块Multi—Axis Curve machining，使用螺纹轮廓交点形成的螺旋线驱动刀具，可以生成带刀轴摆动的加工程序。关键程序段如图11所示。

图11 刀轴摆角关键程序段

使用Alzmetall生产的GS1000/5T机床加工，该机床系统为海德汉TNC 640。刀具尺寸Dt=9.82，Rtool=0.099，单齿铣刀，实切剖切结果如图12所示。图12(a)为非摆角状态下齿形，螺纹根部可见水平方向的刀痕；图12(b)为摆角1.9507°的状态下齿形，螺纹根部未见水平方向刀痕。

图12 0.5-20UNJF-3B螺纹铣削结果

3 讨论

1）在摆角状态下，铣削螺纹面的干涉小于非摆角状态下的干涉。因此，刀轴进行合适的摆角可以减少加工干涉。

2）将摆动角度设定为中径升角，方便快速地控制干涉。

3）通过刀轴摆角，可以控制刀具直径对小尺寸螺纹精度的影响。特别地，由于小尺寸螺纹铣刀的制造难度和小尺寸螺纹公差较小，刀轴摆角铣削螺纹在小尺寸螺纹铣削上有明显优势。

4）刀轴摆角铣削可以改善螺纹螺纹根部表面质量，提高根部尺寸精度。

5）本实切的机床具有C轴无限回转功能，若机床不能实现某角度无限回转，刀具轨迹相对复杂。

4 结语

通过论证，可知基于刀轴摆角的螺纹铣削方法可以减少干涉，使用螺纹中径升角进行摆角数值设定简便快速地减少干涉；刀轴摆角铣削螺纹还可以改善螺纹牙底的尺寸精度和表面质量。基于CATIA编程模块实现了摆角程序的编制，通过实际切削验证了刀轴摆角铣削螺纹的可行性，并完成样件制造。