考虑负效应的垃圾回收两级选址-路径模型与算法

马艳芳，张 文，李宗敏，闫 芳，郭凌云

（1.河北工业大学 经济管理学院，天津 300401；2.四川大学 商学院，成都 610064；3.重庆交通大学 经济管理学院，重庆 400074；4.重庆市环卫集团有限公司，重庆 401121）

0 引言

研究发现，建立临时中转站，构建高效的医院-中转站运输模型是解决城市医疗垃圾运输问题的关键方向之一［1］。Liu 等［1］结合环境影响评价指南，采用免疫算法建立中转站选址模型；然后采用蚁群-禁忌混合算法，建立医院与中转站之间的路径优化模型；最后用武汉市作实例取得了良好的验证效果。Babaee Tirkolaee 等［2］研究了具有时间窗口的选址-路径问题（Location-Routing Problem，LRP），构建以废物收集车辆的总行驶时间最小、时间窗口违规数量和居住在处理设施地点周围的人口数量最小化为目标的多目标模型，为高效地收集、运输和处理医疗废物给各国家提供了参考。赵佳虹等［3］根据环境系统的动态性，设计时变“环境-人口”风险度量模型，建立风险最小和成本最小的多目标选址-分配模型，可根据决策者偏好提供多个有效优化方案。这些研究为医疗废物管理提供了新思路，但大部分仅考虑单级选址路径。虽然废弃物暂存点或中转站的建立十分必要，但是最终端的处理地点（焚烧站）也需重视；因此本文考虑两级选址-路径问题（Two-Echelon LRP，2E-LRP）。

2E-LRP 是复杂的组合优化问题，众多学者致力于该类问题的研究。Jacobsen 等［4］是首先考虑选址-路径问题中多阶存在性的经典代表，提出了三个建设性启发式求解模型。虽然有不少学者提出运用纯精确算法解决两级问题［5-7］，但由于2E-LRP 包含多个非确定性多项式（Non-deterministic Polynomial，NP）问题，常常会加入不止一种启发式法，尤其在求解子问题选址-路径问题（LRP）的过程中使用。马艳芳等［8］在求解多个决策主体下的LRP 时设计了遗传和粒子群混合算法；胡大伟等［9］在求解两级选址-路径模型时，采用改进的两阶段模拟退火（Simulated Annealing，SA）算法，求解时间明显少于商业求解软件CPLEX。鲸鱼优化算法（Whale Optimization Algorithm，WOA）虽然广泛应用于各个领域［10-12］，但关于2E-LRP 的研究较少。本文将改进WOA 与SA算法结合，用于求解所提两级多目标选址-路径（Two-Echelon Multi-Objective LRP，2E-MOLRP）模型。

本文结合目前国内具体情况，借鉴前人的研究思路，研究在物流网络中同时考虑垃圾中转站和焚烧站的两级选址-路径问题。除了考虑经济目标之外，同时把焚烧站运行时对周围居民产生的影响量化为负效应值作为目标函数。为求解所提2E-MOLRP 模型，设计鲸鱼-模拟退火多目标算法WOA-SA；改进初始化方式，采用非线性动态惯性权重系数和非支配排序方法以得到更好的结果；最后，基于2E-LRP、LRP 两组基准案例进行算法对比分析，验证WOA-SA 的寻优能力、收敛性和稳定性，再结合天津市实际情况验证两级多目标模型的适用性。

1 问题描述

1.1 两级选址-路径问题

两级选址-路径问题（2E-LRP）的两级物流网络由若干个备选焚烧站、若干备选中转站以及一些日常垃圾产生点（以下简称垃圾产生点）组成。收集过程中，垃圾首先在产生点被车辆收集，然后被送至暂存中转站，被简单处理后运到焚烧站处置，其中：焚烧站与中转站及相应路径构成一级运输网络；中转站和垃圾产生点及相应收集路径构成二级运输网络。具体网络结构如图1 所示。

图1 两级物流网络结构Fig.1 Two-echelon logistics network structure

1.2 负效应

垃圾收集与处置是为城镇居民创造更好的居住环境，但焚烧站或中转站在运行时会产生污染，某些特殊背景下，这种有害健康的设施更会带来心理上的排斥；垃圾处理设施对周边居民产生的负面影响应当被考虑。

负效应是指设施运行对人体健康、生命或生存造成的负面损害。大多数人将讨厌效应定义为与设备容量正相关、与两个节点之间的距离负相关的函数，并假设负效应在所有方向上一致传播［13］。垃圾在焚烧站处理过程中会产生废气，气体传播速度与风向和风速有关，所以并不是所有的居民区都受到同样的影响，因此，本文考虑所选节点的气候，建立了与风向和距离有关的负效应函数。

定义焚烧站为点(xi，yi)(i∈B)，附近居民区节点为(xj，yj)(j∈P)，dij为焚烧站与居民区节点之间的欧氏距离，两点间直线与当前风向的夹角为θij，ωij(dij)是与距离有关的负效应参数。若两点间距离一定，θij在0°到90°之间增长时，风速在两点间直线方向分量减小，则对居民区产生的负效应值也会减小；若只有距离为变量时，居民区受到最大的负效应影响值为Mi，在距离阈值[di，1，di，2]内随着速率mb逐渐减小，在di，1以内负效应值均为Mi，在di，2以外均为0。此外，负效应值还与焚烧站的规模正相关，处理的废弃物数量越多，对周边造成的影响越大。

负效应参数ωij(dij)的示意图如图2 所示，其公式为：

图2 负效应参数ωij(dij)的二维与三维示意图Fig.2 2D and 3D schematic diagrams of obnoxious effect parameter ωij(dij)

2 2E-MOLRP模型构建

2.1 模型假设

1）候选焚烧站、中转站和垃圾产生点的数量、地理位置、固定成本已知，各级运输车辆固定成本已知，垃圾产生点的垃圾量已知。

2）各级物流设施容量已知，分配给各级物流设施的总需求量不能超过设施的容量限制。

3）各级配送车辆容量已知，各运输路径上车辆载重不能超过容量限制。

4）各节点间距离按照欧氏距离计算，各级运输车辆单位长度运输成本已知。

5）每个垃圾产生点只能被一辆车服务一次，各级运输车辆从物流设施节点出发并返回相同物流设施节点。

2.2 符号说明

本文所使用的符号说明如表1 所示。

表1 参数定义Tab.1 Parameter definition

2.3 模型建立

式（1）～（2）是模型的目标函数：式（1）是负效应目标函数，最小化垃圾焚烧站对周围居民产生的环境影响，与垃圾焚烧站的容量、周围居民数量、和负效应参数ωij(dij)有关。式（2）为二级网络相关的经济成本，由六部分组成，依次为：垃圾焚烧站的开放成本、中转站的开放成本、第一级配送网络中的车辆固定成本和运输成本、第二级配送网络中的车辆固定成本和运输成本。

式（3）～（4）保证开放的垃圾焚烧站和中转站数量合理：

式（5）表示回收设施在一、二级路径上回收的垃圾数量不超过其自身容量：

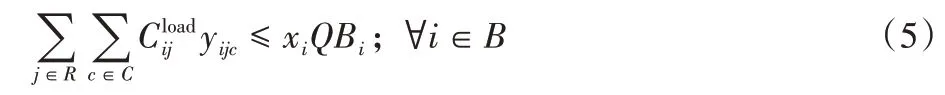
式（6）保证每个被选择的垃圾中转站只能被一辆一级配送车辆服务一次，未被选择的中转站不能被服务：

式（13）～（15）保证一个垃圾产生点只分配给一个垃圾中转站，且只有开放的垃圾中转站才能有车辆进出：

式（22）表示如果一辆车的当前载重加上下一点需求若小于车辆容量，它就会服务下一点：

式（23）保证垃圾中转站发出的车辆总数不能超出其拥有的数量：

式（24）～（25）表示垃圾产生点的垃圾量和弧（i，j）上的车辆载荷均非负：

式（26）保证开放的垃圾中转站容量能够满足垃圾产生点的需求：

3 非支配WOA-SA设计

2E-MOLRP 是NP 难问题，因为包括了几个已知复杂问题：两级设施选址问题、两级车辆路径问题、多目标优化和有容量约束选址-路径问题，因此很难用精确方法求解。本文设计了非支配WOA-SA 求解模型，算法的流程如图3 所示。

图3 本文算法流程Fig.3 Flow of proposed algorithm

3.1 第一阶段：WOA-SA

第一阶段要求解的问题可视为单层选址-路径问题（LRP），中转站的选址极其重要；涉及大量垃圾点的分配，路径的优化可节约大量物流成本，合理的选址也利于一级网络成本优化。为更好地求解第二级物流网络问题，采用混合启发式算法WOA-SA，在改进的WOA 之后运用SA 算法以增强找到的最佳解决方案。

WOA 是澳大利亚学者Mirjalili 等［14］根据座头鲸的狩猎方式提出的一种群智能优化算法。WOA 和其他智能优化算法一样，在求解复杂优化问题时，存在迭代后期种群个体多样性减少、易陷入局部最优的缺陷。

Kirkpatrick 等［15］提出基于单一解的模拟退火（SA）算法可以克服局部最优陷于停滞的缺陷，该算法利用一定的概率来接受较差的解，从而加强跳出局部最优的能力。Mafarja等［16］证明了WOA 和SA 的结合方式优于WOA 的性能，并且大量实验结果表明在WOA 之后再使用SA 比在WOA 中嵌入SA 的效果更好。本文借鉴此思路加以改进作为第一阶段算法，求解中转站选址问题及第二级运输路径。

3.1.1 编码与解码

本阶段研究垃圾产生点（客户）的垃圾收集路径和中转站选址两个子问题，车辆向量、顺序向量和车辆所属中转站的中心向量表示一个完整的解。

X=｛X1，X2，…，XN｝表示鲸鱼群的位置，N是客户数，X1，X2，…，XN是区间（1，K+1）生成的随机数，K是车辆个数。鲸鱼位置编码X的整数部分表示二级路径上每位顾客对应的被服务车辆编号，在解码中由Xk表示，即每位顾客对应的被服务车辆。鲸鱼位置编码X的小数部分表示顾客被服务的顺序，在解码中由XS表示，降序排列，即小数部分越小对应顾客被服务的优先级越高。R是中转站个数，XR为随机生成的K个（1，R）内整数，表示每辆车所属中转站。该编码方式能够满足模型中对于中转站的一些约束，例如：保证被选中的中转站数量至少为1 但不超过候选个数，每个客户只能被一个开放的中转站服务，满足约束中的式（4）、式（13）～（17）、式（21）和式（23）。同理，焚烧站的数量和它与中转站之间的关系也能足约束式（3）、式（6）～（8）。

设有4 个中转站、10 个客户和3 辆车，则编码解码的示例图如图4 所示。

图4 编码与解码示例图Fig.4 Schematic diagram of coding and decoding

从图4 可以看出，在第二级物流网络中选择开放编号为1 和2 的中转站，共派出3 辆车服务10 个客户。例如，Xk中1对应客户2、3、5，对应XS中数字8、6、4，对应XR的第一个数字为1，则车辆1 从中转站1 出发先后服务客户5、3、2。此解的完整表示如图5 所示。

图5 2E-LRP的决策示例Fig.5 Decision example of 2E-LRP

3.1.2 初始化种群

WOA 是基于种群的算法，标准WOA 一般随机生成初始化种群。本文希望得到一个良好的初始化种群，为后续提供一个良好的开端，避免计算资源的浪费；也希望种群具有良好的多样性，降低算法复杂度且不易陷入局部最优。因此，本文采用不止一种初始化方法来解决当前的问题。首先，采用聚类的方法来分配客户给中转站；然后，同时采用随机方法与Clarke 和Wright（Clarke and Wright，CW）节约算法生成初始车辆路径（其中：80%的初始种群是随机的；20%由CW生成）。CW 中节约距离计算公式为：

聚类方法如下。

步骤1 计算所需最少回收中心个数。

步骤2 随机从R中选取Num个中转站，将选定的序号放入集合C中，每个集合都有一个对应的空集合Si。

步骤3 计算客户点I=(xi，yi)与每个选中中转站R=(xj，yj)之间的距离并排序，把客户分配给最近的中转站R，即客户I∈SR。计算两点间的距离：

步骤4 计算每个集合SR中的客户数量，并按降序排序，选择排名最高且未被选中的中转站开放。

步骤5 根据中转站容量分配客户。

3.1.3 WOA-SA更新流程

在WOA 的三个捕捉猎物阶段游走位置不同，因此算子的更新公式也各不相同。当|A| ＜1 时，下一代计算公式为：

其中：t为当前迭代次数；X*、X分别是当前最佳和目前个体的位置向量；A、C、B是系数；r为［0，1］的随机向量；a从2 到0递减；b是对数螺线形状的常数；l在［-1，1］均匀分布；p为［0，1］的一个随机数，表示每种包围方式的概率。图6 举例说明式（30）的更新过程。

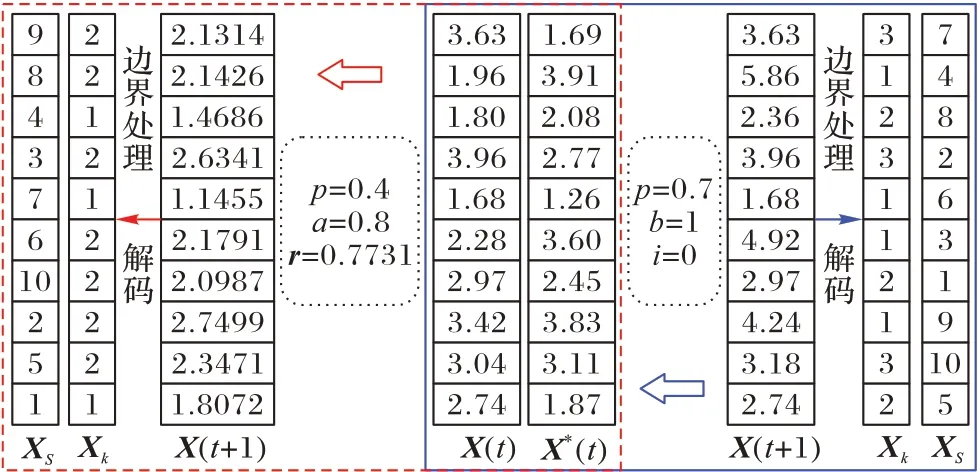
图6 WOA的更新过程Fig.6 Update progress of WOA

为了执行全局搜索，Xrand为随机数，通过随机更新而不是依赖迄今为止找到的全局最佳个体解来选择下一代个体位置。此时A∉(-1，1)，具体公式如下：

由此可以看出WOA 设置的参数较少，全局与局部搜索的平衡由参数A决定，而根据式（31）可知它跟a密切相关：a越小代表算法局部搜索能力越好；反之全局能力增强。在复杂的函数优化中，无法保证a线性减小的规律易导致算法陷入局部最优。针对上述不足，引入余弦非线性控制因子，前期a从2 缓慢减小利于充分的全局搜索，后期下降速度加快促进算法收敛，表达式如下：

此外，文献［17］指出权重因子也会影响算法性能：当权重因子较大时，其搜索范围较大，有利于全局搜索；当权重因子较小时，可在较小范围内执行高精度搜索。为了增强WOA 的寻优能力，采用非线性动态惯性权重系数，更新公式如下：

其中ω(t)i代表第t代第i个搜索代理的权重，公式如下：

其中：f(t)avg、f(t)min、f(t)max是适应度值的平均、最小和最大值；ω1、ω2是初始值；Tmax为最大迭代次数。当个体优于平均水平时，权重减小保留该个体，加快算法收敛；反之促使它向最优个体靠近，增强算法全局搜索能力。

在WOA 得到最优解之后，利用SA 算法避免陷入局部最优解，具体流程可参考文献［16］，此处不再赘述。

3.2 第二阶段：精确求解一级网络

第二阶段求解时已知中转站信息，简化第一级物流网络问题为多目标选址-路径问题。先计算所有被选中的中转站需求，然后精确求解目标函数式（1）～（2），适应度函数的设置在下文详细介绍。两个目标会产生非劣解，因此使用快速非支配排序与拥挤距离计算方法［18］：建立一个帕累托解集的存档E，把得到的解放入存档；通过非支配排序，根据非支配关系将每组解决方案排列到不同的前沿，拥挤距离计算机制用于确保非支配解的分布尽可能均匀。此外，每当帕累托解集存档存储已满时，在存档的删除操作中再次使用拥挤距离计算。算法1 描述了拥挤距离的计算过程。最后给出一组完全非支配的帕累托解集供决策者参考。

3.2.1 适应度函数

在WOA-SA 中，每个个体的适应度值能够反映目标值，据此判断个体优劣。本文考虑设施和车辆的容量约束，对于违反约束的个体设置一个足够大的惩罚值，避免生成不可行解。在第一阶段，只考虑中转站的选址-路径问题，求解的目标函数是式（2）中的一部分，因此该适应度函数的设置也适用于第一阶段算法。当满足容量约束时，以目标函数式（1）～（2）作为适应度函数，当违反容量约束时，则采用带有惩罚值的适应度函数：

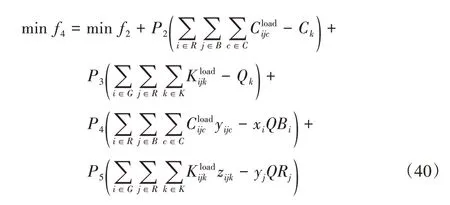
其中：P1、P2、P3、P4和P5是惩罚因子，P1对应负效应函数，P2和P3对应违反焚烧站和中转站容量的情况，P4和P5对应违反一、二级车辆容量的情况。通过适应度函数的设置，保证模型中约束的实现，如与车辆容量有关的约束为式（9）～（11）、式（18）～（20）、式（22）～（26），设施容量约束为式（5）和式（12）。

3.2.2 拥挤距离计算

拥挤距离计算的伪代码见算法1。

4 基准案例测试

首先，选用两组经典基准进行测试，验证本文算法的性能，包括一组2E-LRP 算例［19］和一组LRP 算例［20］。两个算例集合都属于国际通用案例，已经被诸多学者引用测试［21-23］，均可在http：//prodhonc.free.fr 下载。其次，结合天津案例，验证考虑负效应的两级多目标模型的合理性。本文构建的数学模型与算法使用Matlab R2012a 编码，在Dell XPS 13 笔记本运行，Intel Core i5-7200U 处理器2.70 GHz，操作系统为Windows10（64 位）。

4.1 算例参数设置与描述

本文算法涉及的参数主要有：迭代次数、种群规模、惯性权重、初始温度、终止温度、降温速度和较差解的接受概率等。通过实验测试并参考文献［8，16］，设置迭代次数为200，种群规模为30，ω1=0.4，ω2=0.9，T0=1 000，T=1/1 000，降温速度q=0.96，较差解的接受概率设定为p=，内循环迭代次数设置为50。

本文选用Nguyen 等［19］提出的2E-LRP 算例中的一组来验证所提算法的有效性，该算例由Prins 等［24］提出的一级LRP 算例改进而来。在LRP 基础上添加坐标（0，0）作为主仓库，将原始仓库作为中转站，并且假设从主仓库到中转站的距离是两倍的欧几里得距离。选取的24 个案例具有以下特征：客户数量n∈{20，50，100}；中转设施数量m∈{5，10}；客户聚类个数β∈{1，2，3}；二级车辆容量Q∈{70，150}；一级车辆的容量是最大中转站容量的1.5 倍；一、二级车辆的运输成本分别通过距离乘以200 和100 并四舍五入计算得到。每个算例的命名格式为“n-m-β”或“n-m-βb”，后缀“b”表示算例中Q=150。

考虑到一级物流网络中涉及焚烧站和中转站的数量点较少，而单级选址-路径问题更广泛，所以选取LRP 基准案例进行测试。除了Prins 等［24］提出的LRP 算例，较为流行的还有Barreto 等［20］提出的LRP 算例，他总结了诸多前人研究的算例，并改进部分车辆路径问题算例。

本文选取11 组算例，数据与Prins 算例［24］的主要区别在于无车辆固定成本，客户数量n∈[20，100]，设施个数m∈[5，10]，车辆容量各不相同，具体可参考文献［20］，每个算例的命名格式为“人名-n-m”。

4.2 算法对比分析

为评估本文算法的性能，将本文算法求解基准案例的结果分别与目前已知最优解（Best Known Solution，BKS）和现有其他算法的求解结果进行了对比。对比结果如表2 所示，其中：差值Gap为本文算法最优计算结果Best与BKS的比较，计算公式为Gap=100%*(Best-BKS)/BKS。

选取的对比算法为：多起点局部搜索（Multi-Start Iterated Local Search，MS-ILS）算法［19］、带学习过程的贪婪随机自适应搜索法（Greedy Randomized Adaptive Search Procedure × Learning Process，GRASP×LP）［21］、带路径重连的贪婪随机自适应搜索法（Greedy Randomized Adaptive Search Procedure × Path-Relinking，GRASP×PR）［21］、SA［22］和带路径重连的多起点混合启发式（Multi-start Hybrid Heuristic with Path Relinking，MHH-PR）算法［23］。可以看出，MS-ILS 算法整体表现良好，在大规模算例中求得最优解次数最多，其次是SA。与MS-ILS 算法相比，本文算法求解大规模算例的能力较弱，只有100-10-2b 和100-10-3 两个案例求解结果优于其他对比算法；但本文算法在中小规模算例中均能找到最优解，且总体上平均值为188 718，仅次于表现最优的MS-ILS（188 308），差值的平均值仅为0.37%。

表3 为不同算法对Barreto 等［20］提出的11 个LRP 基准案例的求解结果对比。对比算法为多起点偏差随机（Multi-Start Biased-Randomized Heuristic，MSBRH）算法［25］和有偏随机变邻域搜索（Biased-Randomized Variable Neighborhood Search，BR-VNS）算法［25］。表3 中记录了各算法运行10 次的平均值、最优值以及本文算法与最优值的差值，每个案例的最优结果和平均值用粗体标识。从表3 可以看出，除Ch69-100×10 外，本文算法能找到所有案例的最优解，且多次运行结果的平均值也都是3 个算法中最优的。

表3 不同算法求解Barreto案例的结果比较Tab.3 Results comparison of different algorithms solving Barreto case

结合表2～3 可以看出，本文算法在求解顾客规模小于100 的时候均能找到最优解；在大规模算例中虽不能全部找到最优解，但是与其他算法差距不大，具有一定的竞争力。

表2 不同算法求解Prins案例的结果对比Tab.2 Results comparison of different algorithms solving Prins case

4.3 算法收敛性及稳定性验证

为探究提出的WOA-SA 在求解不同规模算例的能力，记录算法求解案例时每代运行结果并绘制迭代图。选取顾客数量为21、50、88 和100 的4 个案例，收敛曲线如图7 所示。可以看出50 代以内算法快速下降，100 代左右已收敛于最优值附近，100 到150 代之内下降趋势减弱逐渐到达最优结果。

图7 本文算法求解Barreto案例的收敛曲线Fig.7 Convergence curves of the proposed algorithm on Barreto cases

为进一步验证算法性能，检验算法稳定性。将4.2 节中35 个基准案例均运行10 次的结果与BKS 的差值绘制为箱型图，以观察不同算法求解案例差值的离散程度。从图8（a）可以看出，求解2E-LRP 案例时，本文算法的异常值最少；虽然矩形的高度不是最短（仅次于MS-ILS），但是远小于MHHPR 算法，且总体高度明显低于GRASP×LP 和GRASP×PR 算法。从图8（b）可以看出，求解LRP 案例时，本文算法存在一个异常值（Ch69-100×10），但是矩形高度很低，这说明数据分布集中。

此外，绘制3 种算法对Barreto 案例中前10 个案例的求解结果均值的条形图，如图8（c）所示。本文算法结果在大多数情况下都低于其他两种算法。

图8 算法稳定性分析结果Fig.8 Algorithm stability analysis results

综上所述，WOA-SA 无论是求解2E-LRP 还是LRP 案例，在不同规模中都具有较强的稳定性。

4.4 实例应用分析

为验证所提模型与算法的适用性，以天津市垃圾回收问题为案例，解决垃圾暂存中转点与焚烧站两者的选址以及中间路径规划问题。

4.4.1 天津市案例描述

外卖打包和快递便利了生活，但也导致了垃圾数量急剧增长，其回收与处理工作已引起政府高度重视。具体到各市区的社区地理位置已知且稳定，选取垃圾点个数为50，候选中转站个数为6，候选焚烧站个数为3。备选焚烧站（A）和中转站（B）的经纬度信息、开放成本和容量的具体信息见表4。它们均拥有足量的车辆以供调配，一级车辆能力为5 000 kg，固定成本400 元；二级车辆容量为1 000 kg，固定成本150 元。垃圾点的经纬度信息和需求量信息见表5，为了表述方便，用编号代指真实地名，且只展示了前10 个地点。

表4 候选站点的信息Tab.4 Candidate stations information

表5 垃圾点的部分信息Tab.5 Part information of waste stations

相关的公路网、行政区域、人口信息数据由天津市交通厅和天津市区域地理数据库获取。除经济成本外，决策者还考虑焚烧站对周围居民的负效应影响，提出的负效应函数与当地气候相关，因此在中国天气网等平台获取天津市风向信息。天津市风向具有明显的季节变化特征：冬季，西北风、北风多；夏季有东南、南风；春秋两季，西南风比较多。设t=｛1，2，…，9｝分别代表9 种常见的风向，其中第9 种风是静风，每年有45 天是静风，其余8 种风向各40 天。此外，负效应函数根据距离划分三段式，选取两个阈值分别为0.5 km和1.0 km［15］。

4.4.2 2E-LRP模型分析

运用本文算法求解天津市案例，设置种群规模为30，迭代200 次，运行10 次记录结果。

第一阶段算法求出的第二级物流网络最优选址决策为开放候选点序号为2，3，5 的暂存中转站，经济成本为91 319.30 元。其他选择可有1，2，5（91 449.12）或者2，4，5（91 398.33），都需派发8 辆车服务50 个顾客。虽然第一种的成本目前最小，但是还要累加一级物流网络的经济成本，如中转站4 距离焚烧站3 较近而离焚烧站2 比较远，而中转站1 距离焚烧站3 最远而离1 和2 较近。

第一级物流网络中开放焚烧站的成本是一样的，因此经济成本的决定因素在于开放的中转站与焚烧站之间的距离。从图9（a）可以看出，焚烧站2 距离大多数中转站较近，服务路程短，但是否开放编号为2 的焚烧站还应考虑另一个负效应目标。

4.4.3 多目标分析

一级物流网络决策者只需开放一个候选焚烧站即可，因考虑到设施运行对周边居民产生的负面影响，需平衡经济成本和负效应值这两个目标。运行结果如图9，表6 给出几个推荐方案的数据。

图9 天津市案例信息图Fig.9 Information maps of Tianjin case

表6 天津市案例的帕累托解集Tab.6 Pareto solution set of Tianjin case

从表6 可以看出，焚烧站2 的经济成本明显低于焚烧站1、3，但是焚烧站2 周围居民区较1、3 更为密集，负效应值最大；焚烧站1 和3 的经济成本和负效应值无明显差异。综上所述，若决策者更注重社会影响则可开放焚烧站1 或3；若可接受焚烧站2 的负效应影响则可节约许多经济成本。

负效应值与设施附近居住人口数量有关，该参数稳定无法通过算法优化，因此选取帕累托解集中有最优路径的解展示，如图9（c）所示。一级网络用虚线表示路径，派出至少2辆车服务；二级网络路径用实线表示，共8 辆车，分别用不同颜色展示。它们的装载量分别为：900、930、980、970、910、950、900 和860 kg，均在容量范围内且利用率合理。

4.4.4 灵敏度分析

为验证负效应函数的合理性，对相关参数设施容量（QB）和附近的人数（p）进行了灵敏度分析，分析结果见表7，第一列是参数变化幅度，以最优成本291 595 为基准。

表7 模型参数灵敏度分析Tab.7 Sensitivity analysis of model parameters

总体而言，负效应值与两个参数呈正相关，但在不同的变化区间内波动幅度不同。当参数降低到一定程度时，负效应值趋于稳定，因为设施一旦运行就会对周围环境产生影响。当需求未超出设施的容量时，人口增长导致负面影响的缓慢增加。但增长到一定程度（115%）时，负效应值激增，可能产生垃圾的数量超过现有设施的容量，需开放新设施。当其他参数不变时，设施容量小范围变化时目标值变化幅度稳定，若容量过大，即使处理垃圾不多波及半径也会增大。

此外，还对二级车辆载重（QK）和垃圾量（q）进行分析，以验证参数对经济目标的影响。车辆载重QK越小，使用数目越多，经济成本越高。但是，当QK增加到一定程度（115%）时，车辆的固定成本将非常高，造成经济浪费。还有，参数q与经济成本呈正相关，但是当q增加到110%时，经济成本显著增加，这表明需求超过了目前设施容量，必须开设一个新的设施来服务客户。

灵敏度分析的结果清楚地表明应在人口稀少的区域建设适当规模的垃圾处理设施，并应选择适当大小的车辆。

5 结语

本文研究垃圾的收集、运输、处理问题，构建两级多目标选址-路径模型，通过优化中转站和焚烧站的选址及路径问题，以达到负效应最低和经济成本最小化的目标。

为求解提出的模型，设计改进的两阶段WOA-SA 非支配算法：1）初始化方式，先聚类分配客户到中转站，后用随机（20%）和CW（80%）同时初始化路径；2）采用非线性动态惯性权重系数调整收敛速度以增强WOA 的寻优能力；3）采用WOA 和SA 并行结构加强算法跳出局部最优的能力；4）运用快速非支配排序方法确定帕累托解集以供决策者参考。

为验证算法求解2E-LRP 的能力，选取24 个2E-LRP 基准案例，与已知5 个对比算法的结果进行对比分析。在13 组数据中，本文算法均优于其他对比算法，总体平均提升了0.37%。为验证算法求解LRP 的能力，选取11 个LRP 基准案例，与其他对比算法相比，本文算法能找到除Ch69-100×10外其他所有案例的最优解，且总体差值平均值（0.08%）是最优的。测试了算法收敛性和稳定性，结果表明算法在前期快速收敛于最值附近，且在不同规模的算例中表现稳定。

此外，设计基于距离和风向的负效应分段函数，结合当地气候，考虑设施与顾客点直线方向和风向的夹角，使其更加贴合实际情况。为验证所提模型和算法的适用性，选取天津市为分析对象，给出三种不同选择方案的负效应值以及经济成本供决策者参考，并给出最优经济成本时的路径方案。

实验结果表明，本文模型与算法具有广泛的适用性，为生活垃圾的收集处置给各地政府提供决策支持，也为其他类型的垃圾处置提供思路。但是本文也具有一定的局限性，比如医疗类废弃物的处理不仅需要考虑设施的影响，还需要考虑运输风险，未来可就此进一步研究。