GPT3模型中国区域大气剖面应用精度分析

王来顺,刘建忠,张寅宝

(郑州大学 地球科学与技术学院，郑州 450001)

全球导航卫星系统( global navigation satellite system，GNSS) 信号穿过中性大气时，会受大气折射影响产生延迟，在天顶方向被称作对流层天顶延迟(zenith total delay，ZTD)。在GNSS测量中，ZTD是一个十分重要的误差源[1]，也是GPS气象学重要研究对象[2]。ZTD由干延迟和湿延迟两部分组成，并可以通过两者相应的映射函数投影到任意信号传播路径上[3]。为模型化ZTD，学者们通过分析电磁波在大气中传输过程，基于实测气象数据建立对流层延迟经验模型[4]。常见的对流层延迟改正模型大致分为两类：气象参数模型和非气象参数模型。其中气象参数模型包括传统的Hopfield模型[5]和Saastamoinen模型[6]等。此类模型在确定ZTD时精度较高，可达cm级[7]，但该类模型高度依赖实测气象参数，若采用标准大气气象参数，其改正效果较差[8],极大限制模型的使用。非气象参数模型包括EGNOS、UNB系列、GPT系列等模型[9-11]。此外，李薇[8]利用IGS站提供的高精度对流层天顶延迟时间序列和 NCEP 大气资料建立IGGtrop模型；姚宜斌[7]利用GGOS Atmosphere资料提供的全球天顶对流层延迟格网时间序列研究了全球对流层天顶延迟的时空变化特征，在此基础上使用球谐函数对相关参数进行建模，建立GZTD模型。这些模型都是直接对ZTD进行分析建模或对气象参数进行分析建模，均不依赖气象参数，仅需测站位置信息和年积日即可实时计算ZTD值。中国区域地形气候较为复杂，例如在部分区域，测站与参考面之间的高程差异甚至超过2 km[12]，因此许多全球适用的模型应用于中国区域时，难以取得理想的精度，例如，利用2015年的探空资料，GPT2w模型Tm的全球均方根误差(root mean square，RMS)为3.82 K，而其在中国区域为4.43 K[13-14]。此外有新研究指出经验模型不应当仅适用于地表，文献[15]讨论了经验模型在整个大气剖面的应用精度。我国幅员辽阔，地形地貌复杂，气候系统变化多样，气象探空站点分布极不均匀，对流层延迟模型在不同区域精度也会有所不同[16]。鉴于GPT3(global pressure and temperature3,GPT3)是目前公开精度较高的对流层延迟模型，且尚未有文献利用Radiosonde数据讨论其应用于整个对流层剖面的精度，文中基于中国2011—2020年的Radiosonde数据，就GPT3得到的几个气象参数在地表至11 km的应用精度展开分析,为进一步改善模型提供参考。

1 GPT3模型与探空数据简介

1.1 GPT3模型

GPT系列模型是目前较为热门的对流层经验改正模型，包括GPT、GPT2、GPT2w和GPT3[10,11,17,18]4种产品。与GPT2w相比，GPT3增加了梯度模型，改良了映射函数关系，从而有效克服了低高度截止角时引起的映射函数误差[19]。GPT3将全球划分为1°×1°的格网，在每个格网点基于最小二乘法，式(1)拟合各个参数的年周期和半年周期。

(1)

式中:A0表示参数均值;A1和B1表示年振幅;A2和B2表示半年振幅。使用模型时，通过输入经纬度，搜索测站周围4个格网点，调用相应函数，计算出格网点参数值，经高程归化后，线性内插至测站处，即可计算任意位置P、T、E、Tm等所需分析的大气参数值，其计算简单且精度较高，广泛应用于GNSS测量等领域。

1.2 数据源及方法

探空数据是最常见的大气探测手段，理想条件下，经过校准的无线电探空大气温度数据精度为±0.5 ℃，相对湿度精度为±5%[20]。美国国家气候数据中心的全球站点无线电探空资料数据集(the integrated global radiosonde archive，IGRA)(https://www.ncei.noaa.gov/products/weather-balloon/integrated-global-radiosonde-archive)常用于气候分析[21-24]。由于IGRA为直接观测数据，故常用其来对其它数据进行精度评定。文中利用IGRA提供的2011—2020年中国区域82个无线电探空站在各探测高度的气象参数，以此为精确值分析GPT3模型得到的气压(GPT3-P)、气温(GPT3-T)、水汽压(GPT3-E)和加权平均温度(GPT3-Tm)在中国区域地表至11 km对流层剖面的精度，得出其误差的时空分布规律，为进一步精化该模型在中国区域的应用提供参考。

文中采用平均偏差(Bias)、RMS和标准差(Standard Deviation，STD)作为精度评判标准，具体计算见式(2)。

(2)

其中,Bias表示模型与真值的偏离程度，反映模型系统偏差；RMS表示精度，用于衡量模型稳定性及可靠性;STD反映样本离散程度，表示随机误差。

为剔除Radiosonde数据中的粗差，采用如下条件选取数据：

1)从地表起，连续、有效探测水汽压的层数不小于12层；

2)连续、有效探测的顶层水汽压不大于0.015 hPa。

通过以上条件，筛选出中国区域的82个测站供模型验证。

2 GPT3模型精度分析

图1绘出2020年7月3日T12:00武汉站分别由GPT3模型和Radiosonde得出的P、T、E和Tm在各个探测高度的值。

由图1可知，GPT3模型考虑了P和E随高程的指数递减规律，并假设T随高程线性递减。但GPT3模型未考虑Tm的高程递减特性。比较Radiosonde和GPT3模型的廓线，可看出在低高程面各参数估计精度较高，但随着高程增加，整体估计精度都有所降低。其中E在2～4 km区间变化复杂，在6 km以上，接近于0。由于Tm未考虑高程改正，随着高程增加，其误差急剧增大。

图1 2020年7月3日T12:00武汉站 GPT3模型和Radiosonde廓线图

为分析GPT3在中国区域应用于地表至11 km大气剖面精度，表 1分别计算了GPT3的P、T、E和Tm在地表和地表至11 km大气剖面的精度,如表1所示。

表1 GPT3模型中国区域地表及地表至11 km剖面精度统计表

表 1显示，GPT3-P、GPT3-T和GPT3-Tm的地表RMS比应用于11 km以下大气剖面时小，但GPT3-E却呈现相反的现象，其原因可能是随着高度增加，大气水汽含量急剧减少并接近于0，故表现出GPT3-E的RMS较小。但整体而言，GPT3模型在11 km以下的大气剖面的应用精度，小于其应用于地表时。文中基于中国2011—2020年的Radiosonde数据，就GPT3模型得到的几个气象参数在地表至11 km的应用精度展开分析。

2.1 GPT3模型精度的地理分布分析

利用Radiosonde数据分析GPT3得出的4个气象参数在地表至11 km应用精度的空间分布，并结合实验与文献[4]将研究区域按15°～30°N，30°～40°N和40°～55°N分为3个区间，定量分析其精度的空间变化规律。

2.1.1 GPT3-P精度空间分析

绘出各测站GPT3-P的Bias、RMS及STD分布如图2所示。

图2 各Radiosonde站地表至11 km的GPT3-P精度分布图

图2(a)可看出，GPT3-P的Bias在7.36～ 26.35 hPa之间，说明模型存在明显高估现象，其地理分布整体由北向南逐渐减小。Bias最大值为26.35 hPa，位于重庆市，其经纬度和高程分别为29.60°N，106.40°E和541.10 m。分析原始数据，重庆站观测记录仅有19条，可能存在较大误差。Bias在20 hPa以下的测站有73个，占89%；GPT3-P的RMS在10.40～ 29.24 hPa之间。RMS较大的测站多见于中国北部地区。除重庆站外，RMS最大的测站位于41.72°N，82.95°E，1 083.5 m，其值为27.91 hPa。RMS在25 hPa以下的测站有64个，占78%；而RMS在25 hPa以上的测站有 12个在40°N以北。STD最大为22.00 hPa，位于23.90°N，106.60°E，177 m。STD在20 hPa以下测站共有81个。

按3个纬度区间定量分析，结果如表 2所示。

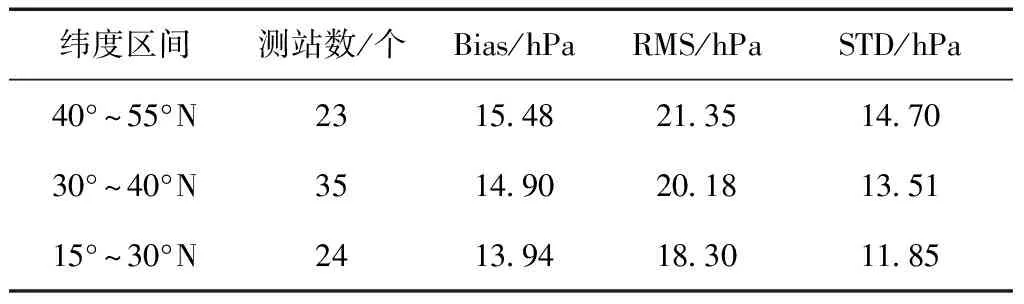
表2 3个纬度区间GPT3-P的精度表

由表2得出，GPT3-P的Bias、RMS和STD都呈现出高纬度地区差而低纬度地区精度较高的空间分布，这与图2反映的规律一致。

2.1.2 GPT3-T精度空间分析

图3绘出各探空站GPT3-T误差分布。

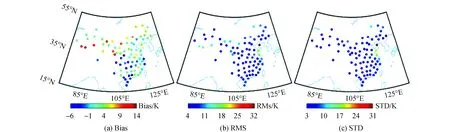
图3 各Radiosonde站地表至11 km的GPT3-T精度分布图

图3(a)表明，GPT3-T的Bias在-6.99～13.26 K之间，其中正偏差较大的测站多见于西北内陆，而负偏差较大的测站则多见于低纬度地区。Bias在-6～6 K之间的测站共有66个，占总体80%。其中正Bias最大的测站值为13.26 K，位于新疆民丰，坐标为37.07°N，82.72°E和1 409 m；负Bias最大的测站值为-6.99 K，位于三亚。RMS和STD最大的测站均为大连站，分别为32.62 K和31.00 K。除大连站外，RMS和STD最大值分别为20.00 K和19.79 K，位于青岛。RMS在10 K以下的测站有65个，占79%。RMS大于10 K的17个测站中有10个位于30°～40°N之间，其余位于40°～55°N之间。STD在10 K以下的测站有 77个，其误差的空间分布与RMS类似。

将各测站按纬度划分3个区间，统计结果如表3所示。

由表3可以看出，GPT3-T的Bias在30°～40°N 区间最小，仅为-0.05 K，但其RMS和STD在该区间却取得最大值，在15°～30°N区间精度最高，这同样和图3反映的结论一致。

表3 3个纬度区间GPT3-T的精度表

2.1.3 GPT3-E精度空间分析

GPT3-E误差分布如图4所示。

图4表明，GPT3-E的Bias在-0.29～2.24 hPa之间，在-0.50～0.50 hPa之间的测站共有65个，占79%。最大正Bias为2.24 hPa，坐标为23.80°N，114.73°E，61 m，位于广东河源。RMS和STD的最大值分别为4.79 hPa和4.23 hPa也都位于河源站。RMS在3 hPa以下的测站有79个，在2 hPa以下的有53个，分别占96%和65%。整体而言RMS的分布由西北向东南逐渐增大，可能是因为东南方水汽丰沛，变化剧烈，难以建模的原因。STD的空间分布与其RMS类似。

3个纬度区间的精度统计值如表4所示。

图4 各Radiosonde站地表至11 km的GPT3-E精度分布图

表4 3个纬度区间GPT3-E的精度表

表4显示，40°～55°N区间Bias为0.04 hPa，表明模型没有明显系统误差，但另两个区间的Bias都为正值，表明GPT3-E存在高估现象。GPT3-E的Bias、RMS和STD都随着纬度的减小而增加。

2.1.4 GPT3-Tm精度空间分析

GPT3-Tm的Bias、RMS及STD的分布如图5所示。

由于GPT3-Tm未考虑Tm高程改正，因此应用于地表至11 km时，其Bias值在14.41～30.34 K之间，模型存在普遍高估现象。就其空间分布而言，在西北内陆和东南沿海都存在Bias较大的测站。RMS在22.30～38.54 K之间，而STD在13.21～24.22 K之间，RMS和STD较大测站也见诸于西北和东南沿海地区。GPT3-Tm精度表明，GPT3-Tm模型仅适用于地表，不适用于高空。

分3个纬度区间精度统计结果如表5所示。

表5 3个纬度区间GPT3-Tm的精度表

由表5得出，由于未考虑高程改正GPT3-Tm在各维度区间的精度都较差，以至于其空间分布规律不明显，在精化GPT3-Tm模型时需要充分考虑其高程改正。

2.2 GPT3模型不同高程的精度分析

为进一步分析GPT3在不同高程区间的应用精度，本节在3个纬度区间内，将11 km以下大气划分为9个区间，分别分析各个气象参数精度变化规律。

2.2.1 GPT3-P不同高程精度分析

GPT3-P在3个纬度区间不同高程精度统计如表6所示。

表6可看出，GPT3-P在1 km以下区间内，在30°～40°N的Bias最小，为1.28 hPa，而在30°N以南区间最大，为4.14 hPa。在1～2 km区间，30°～40°N的Bias最大，在30°N以南区间最小，为

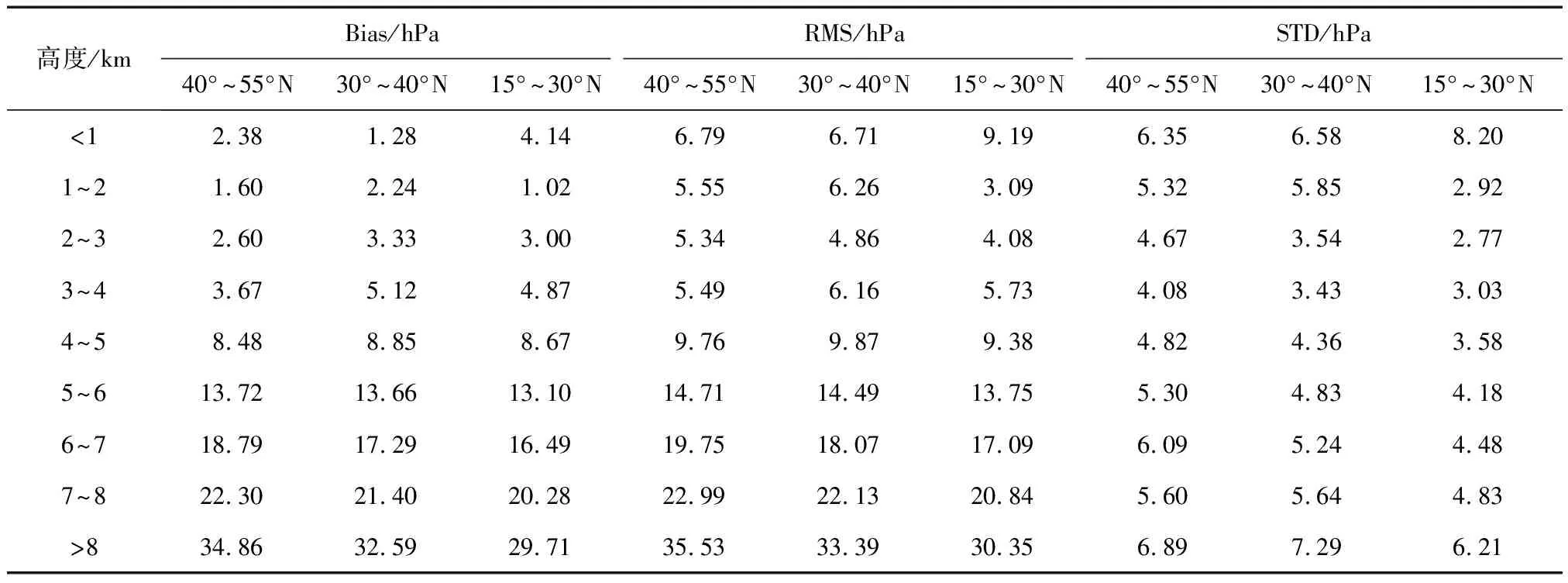
表6 GPT3-P 3个纬度区间不同高程的精度统计表

1.02 hPa。在海拔3 km以上，各区间Bias均随海拔高度增加而增大，在海拔5 km以上，40°～55°N的Bias最大，在15°～30°N区间最小。

1 km以下RMS在区间30°～40°N最小，最大在15°～30°N。在1 km以上，15°～30°N的RMS反而在各区间中最小。30°N以北两个区间都在2～3 km内最小。在5 km以上30°～40°N区间的RMS最大。在2 km以上，各区间RMS都呈现随高程增加而增加的趋势。STD变化规律与其RMS类似。

2.2.2 GPT3-T不同高程精度分析

GPT3-T精度统计如表7所示。

表7 GPT3-T 3个纬度区间不同高程的精度统计表

由表7可得，40°～55°N的Bias在各个高程段都为正值，且在3～4 km内取得最小值0.11 K，在4 km 以上，其Bias随海拔高度增加而增大。30°～40°N的Bias变化复杂，在2 km以下为正值，在2～8 km区间为负值，在8 km以上又为正。其Bias绝对值最大高程段为4～5 km之间。

总体而言，各区间GPT3-T的RMS都随着海拔高程的增大而增大。在海拔3 km以下以及7 km以上，15°～30°N区间的RMS最小；但在3～6 km之间40°～55°N区间的RMS最小；15°～30°N区间的RMS在6～7 km之间取得最小值。

在各高程区间，15°～30°N的STD都较其他两个纬度区间小。在3 km以下，30°～40°N的STD小于40°N以北的区间，但在3 km以上却呈现出相反规律。各区间GPT3-T的STD也都随海拔高度升高而增大。

2.2.3 GPT3-E不同高程精度分析

表8统计了GPT3-E在3个纬度区间不同高程的精度。

由表8可知，在海拔3 km以下，30°～40°N的Bias为正值表明GPT3-E在该纬度和高程区间存在高估现象，但在其他两个区间为负值。在4 km以上，所有纬度区间的Bias都为正。在3～6 km之间，40°N以南两个区间Bias都随海拔升高而增大，但在6 km以上并不存在这种趋势。整体而言15°～30°N区间Bias绝对值在各个高程区间都取得最大值。

表8 GPT3-E 3个纬度区间不同高程的精度统计表

其RMS都随海拔升高而减小，且纬度越小，RMS越大，可能因为中国南方水汽丰沛且变化较大，难以建模；同时高海拔大气水汽含量较少，也导致了其绝对RMS较小。STD与其RMS变化趋势相同。

2.2.4 GPT3-Tm不同高程精度分析

GPT3-Tm在3个纬度区间不同高程的精度如表9。

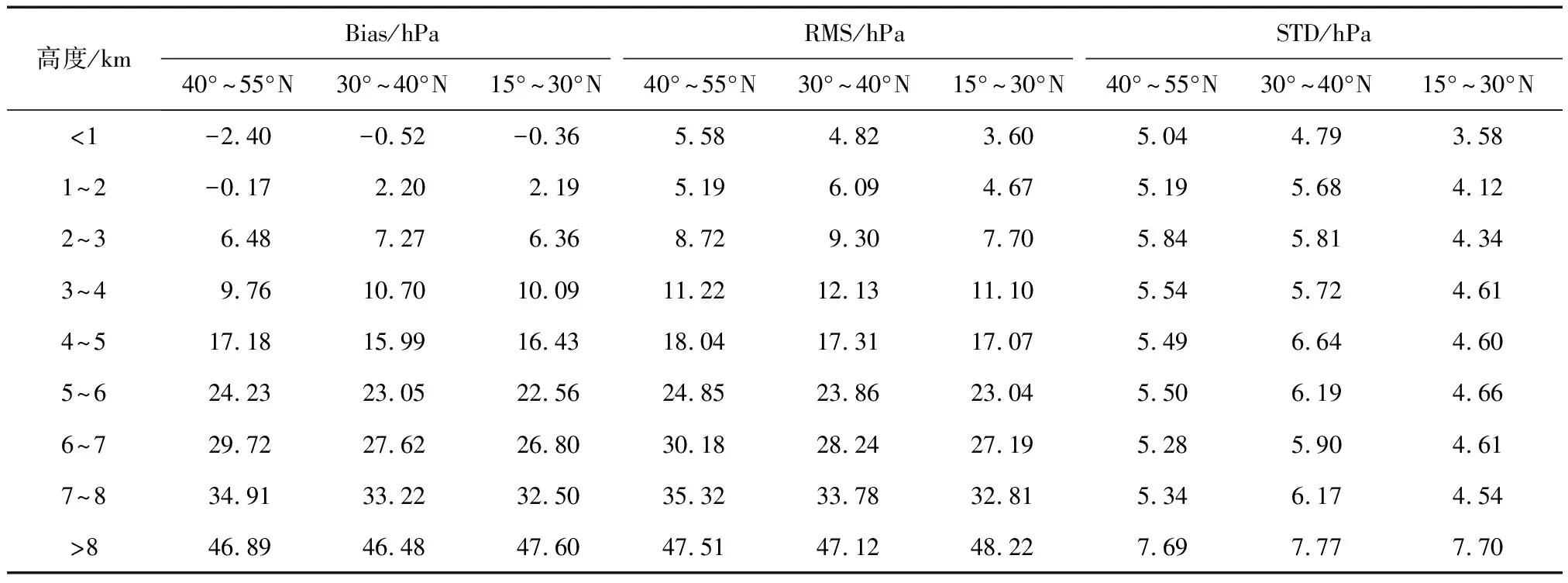
表9 GPT3-Tm 3个纬度区间不同高程的精度统计表

表9可看出，由于未考虑高程改正，GPT3-Tm的Bias、RMS和STD都随高程升高而增大。GPT3-Tm各纬度区间不同高程段的STD远小于其RMS，说明模型随机误差较小。各高程段都表现出低纬度区间精度较高的空间分布规律。因此在进一步精化GPT3-Tm时要充分研究其高程改正规律。

除GPT3-E外，其他各气象参数总体都表现出低海拔的精度优于高海拔的现象，这说明GPT3模型的高程改正方法还有待进一步精化。

2.3 GPT3模型精度时间序列变化分析

为研究GPT3模型精度时间变化规律，本节就GPT3得到的4个气象参数在地表至11 km应用精度的时间序列变化展开分析。

2.3.1 GPT3-P精度时间序列变化分析

图6显示GPT3-P日均Bias、RMS和STD变化。

图6 地表至11 km的GPT3-P日均Bias、RMS和STD变化

由图 6得出，GPT3-P日均Bias均在10 hPa以上，说明模型估值偏高；日均RMS分布在20 hPa附近，整体表现为1—5月上升、5—12月下降的趋势，呈现出一定的季节特性；其STD整体小于15 hPa。

其年均精度变化如图7。

图7 地表至11 km的GPT3-P年均Bias、RMS和STD变化图

图7显示，GPT3-P的年均Bias为正值，说明模型估值偏高；年均RMS与STD的变化较为平稳，总体GPT3-P模型较为可靠。

2.3.2 GPT3-T精度时间序列变化分析

GPT3-T日均精度变化如图8。

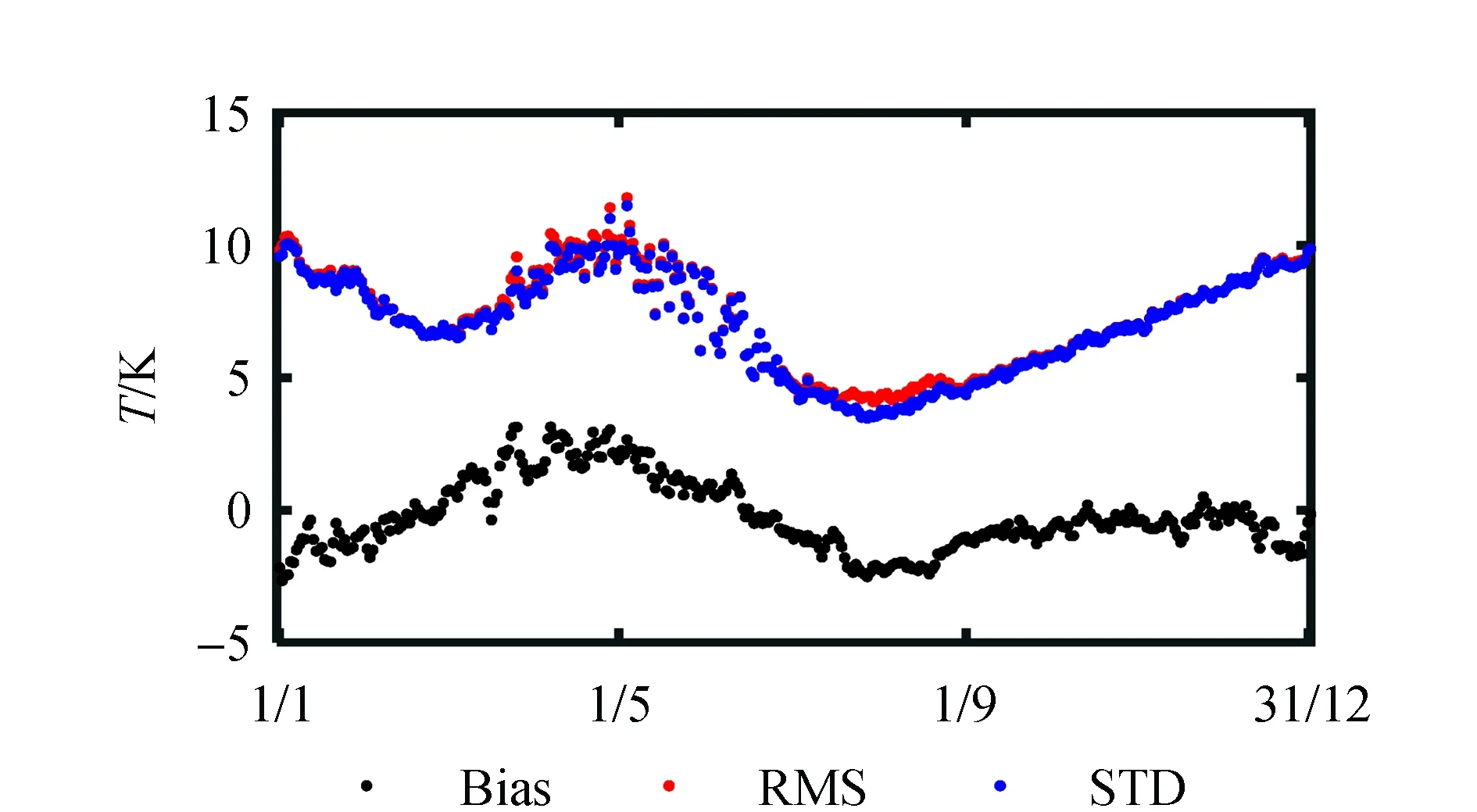
图8 地表至11 km的GPT3-T日均Bias、RMS和STD变化图

由图8，GPT3-T日均Bias在1—5月呈上升趋势，5—9月呈下降趋势，9—12月变化较为平稳；日均RMS整体在10 K以下，在8月最小；日均STD变化与RMS基本相同。

图9绘出了GPT3-T的年均精度变化。

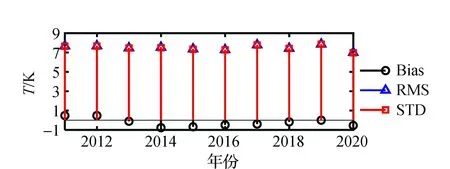
图9 地表至11 km的GPT3-T年均Bias、RMS和STD变化图

图9得出，GPT3-T年均Bias绝对值在1 K以内，说明模型较稳定，无明显系统误差；年均RMS与STD的变化较为平稳，变化趋势基本相同，与图8表现一致。

2.3.3 GPT3-E精度时间序列变化分析

绘出GPT3-E日均Bias、RMS和STD变化如图10。

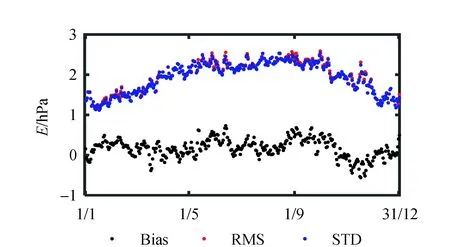
图10 地表至11 km的GPT3-E日均Bias、RMS和STD变化图

图10可看出，GPT3-E日均Bias绝对值在1 hPa以内，模型较可靠；日均RMS整体表现为1—9月逐渐增加、9—12月逐渐减小的趋势，呈现出一定的季节性，可能因为夏季水汽交换较为频繁，精度略低，冬季气温低，水汽活动较少，故精度略高；日均STD变化基本与RMS一致。

图11绘出了GPT3-E年均精度变化。

图11 地表至11 km的GPT3-E年均Bias、RMS和STD变化图

由图 11，GPT3-E年均Bias绝对值较小，其中2016年和2020年Bias接近0，模型无明显系统误差；年均RMS整体变化较平稳，模型精度较高；年均STD变化与RMS类似。

2.3.4 GPT3-Tm精度时间序列变化分析

GPT3-Tm日均精度变化如图12所示。

图12 地表至11 km的GPT3-Tm日均Bias、RMS和STD变化图

可以看出，GPT3-Tm日均Bias均为正值，说明模型高估现象严重；日均RMS整体分布在25 K以上，说明模型在地表至11 km大气层面精度不高；日均STD整体分布在15～20 K之间，模型随机误差较大。

绘出GPT3-Tm年均Bias、RMS和STD变化如图13。

图13 地表至11 km的GPT3-Tm年均Bias、RMS和STD变化图

由图13可得，GPT3-Tm年均Bias、RMS以及STD均较大，说明GPT3-Tm在中国区域的整个对流层剖面精度均不高。

3 结 论

利用2011—2020年中国区域82个无线电探空站相关信息，提取不同测站在各个等压面的气象参数，以此来分析GPT3模型在中国区域的误差特性。从验证结果可知：

1)GPT3在中国区域地表和地表至11 km大气剖面精度分布具有差异性，其中GPT3-P和GPT3-Tm在中国区域地表精度要高于大气剖面精度，而GPT3-E和GPT3-T相反。

2)从误差特性来看，GPT3模型精度受纬度影响较大。其中GPT3-P、GPT3-T及GPT3-Tm精度随纬度增加而减小，GPT3-E反之。就模型稳定性而言，GPT3-P和GPT3-Tm模型高估现象明显，GPT3-T的Bias在30°～40°N区域内最小，为-0.05 K，而GPT3-E在40°～55°N区域内Bias最优，为0.04 hPa。

3)GPT3模型精度与高程具有相关性。GPT3-P在2 km以上，其RMS随高程增加而增大；GPT3-T的RMS随海拔升高而增大，低纬度区域精度较高纬度区域要好；对于GPT3-E，其RMS呈随海拔高度升高而减小，且纬度越小，RMS越大的规律；GPT3-Tm的RMS由于没有考虑高程递减率，导致随海拔升高而急剧增大。

整体而言，GPT3模型提供的P、T、E和Tm在中国地区范围内具有较高精度和稳定性，但要想进一步提升模型预测精度，可在今后模型精度分析基础上，考虑模型应用区域的纬度以及高程，以期获得更加精准的模型。