计及功率响应延时补偿的换流器接口电源等效惯量估计方法

李昭良，胥国毅，王 程，张啸笛，李相俊，毕天姝

（1. 新能源电力系统国家重点实验室（华北电力大学），北京市 102206；2. 新能源与储能运行控制国家重点实验室（中国电力科学研究院有限公司），北京市 100192）

0 引言

在中国加快能源转型并提出“碳达峰·碳中和”目标的背景下，电力系统中风电、光伏等换流器接口电源（converter-interfaced generator，CIG）比例将进一步提高。大量CIG 取代同步电源（synchronous generator，SG）接入电网，如果不附加调频控制，将使系统惯量下降、一次调频能力降低，系统受扰动后频率变化率、最大频率偏差增大［1-2］，加剧频率失稳风险并可能引发大停电事故［3］。开发CIG 的频率控制潜力成为应对系统频率稳定的重要手段和各国并网导则或标准中的要求。惯量作为衡量频率稳定性的重要指标，决定了频率响应动态特性。然而，CIG电源频率响应差异显著，风、光频率控制存在不确定性。因此，评估CIG 的等效转动惯量对研究双高电力系统的频率动态特性、评估考核CIG 频率控制能力、提升CIG 主动支撑电网频率的能力具有重要意义。

目前报道的文献中，惯量评估主要针对传统同步发电机系统，评估方法包括3 类［4-13］：基于准稳态运行的评估、基于小扰动事件的评估和基于大扰动事件的评估。换流器接口内部风光资源出力的随机性和波动性使得利用大量运行数据构建的惯量评估概率或统计模型精度下降［4-5］，造成基于准稳态运行的评估方法应用于CIG 时准确性降低。基于小扰动事件的评估方法，评估精度依赖于小信号模型的精度［6-7］或频域参数辨识方法的选择［8-9］，对采用调频资源配置方式灵活、调频控制方式灵活及有功响应延时上下浮动的CIG，难以建立准确的小信号模型或频域模型。基于大扰动事件的评估方法，当CIG调频控制存在死区和有功响应延时，基于扰动瞬时的惯量评估方法将失效［10-11］，并且一次调频控制的有功功率会显著影响惯量评估的精度［12-13］。因此，由于CIG 与同步机物理结构、控制方式上的差异，对CIG 的等效惯量评估应考虑CIG 自身特性，针对同步机系统的惯量评估方法不能直接应用于CIG。

现有针对CIG 评估方法较少考虑其在频率事件中的真实支撑作用。文献［14］通过建立含虚拟惯性控制的双馈风机简化模型和风电场聚合模型，获取风电场聚合等效虚拟惯性时间常数，但是该方法仅对双馈风机进行建模，对于采用其他调频资源的CIG，该方法的准确性不能得到保证。文献［15］基于SG 转子运动方程原理，计及一次调频功率对惯量评估的影响。然而，该方法未考虑CIG 的非线性环节，当CIG 存在延时、死区等非线性环节时，准确性降低。文献［16］考虑了CIG 非线性环节，在已知微电网中所有同步电源的惯量、扰动功率的大小和准确的频率数据的前提下，对微电网中所有非同步电源的累计惯量进行评估，但是该方法并不适用于单一换流器接口。

针对以上问题，本文基于同步机转子运动方程，从单一CIG 并网点外特性的角度出发，提出一种计及功率响应延时补偿的CIG 等效惯量评估方法。首先，分析CIG 的有功响应特性，提出一种基于能量视角的等效惯量评估方法，并降低一次调频功率对等效惯量评估的影响；在此基础上，提出一种有功响应延时计算方法，利用扰动后CIG 并网点的功率和频率数据计算延时，减少延时对等效惯量评估的影响。

1 CIG 等效惯量分析

同步机的惯量是同步机旋转刚体惯性的大小，描述的是同步机转子抵抗不平衡转矩的能力。系统发生有功功率扰动，造成同步机端有功功率不平衡，同步机机械转速发生变化。若认为扰动后同步机电角速度变化不大，即ω≈ω0，则可以得到同步机转子运动方程：

式中：δ为同步发电机的转子角；ω为发电机的电角速度；ω0为同步转速；Hg为同步机的惯性时间常数；Pmg为原动机施加在同步机转子上的机械功率；Peg为同步机端电磁功率；D为阻尼常数。

为了提高新能源电力系统惯量水平，提升新能源电源主动支撑电网频率的能力，大量研究基于同步机转子运动方程，围绕CIG 并网有功控制技术展开，即虚拟惯量控制技术，按照控制原理可以分为跟网型控制和构网型控制两类。

1.1 跟网型虚拟惯量控制

跟网型虚拟惯量控制在换流器的有功控制环节引入系统测量频率变化率，通过改变有功控制指令，使得新能源电源在系统频率跌落过程中，增发与频率变化率成比例的有功功率，以支撑电网频率［17］，有

式中：ΔPv为虚拟惯量控制增发有功功率；Hv为虚拟惯性时间常数；dfm/dt为量测点频率变化率。

跟网型虚拟惯量控制，其本质为功率源［18］，与同步机转动惯量不同，电流为受控量，电压为非受控量，不具备瞬时承担扰动功率分配的能力，通过模拟转子释放旋转动能以支撑系统频率。

1.2 构网型虚拟惯量控制

构网型虚拟惯量控制利用逆变器出口电势与同步机内电势对应、逆变器一侧滤波电抗与同步机电枢绕组对应，并在换流器控制环节引入同步机的转子运动方程以及电磁暂态方程，使得新能源电源具备与同步机相同的有功-频率和无功-电压控制［19］。

构网型虚拟惯量控制，其电压为受控量，电流为非受控量。理想情况下，构网型虚拟惯量能够体现与同步机惯量相同的性质，能够分担扰动瞬时不平衡功率。但由于调频资源的波动性、调频模块有功响应存在爬坡率，以及在实际应用中为了避免虚拟惯量控制频繁动作，通常输出增加惯性环节缓冲［18］，构网型虚拟惯量控制很难完全体现与同步机惯量等同的性质。

2 CIG 等效惯量评估方法

2.1 CIG 等效惯量评估

在扰动发生后，不考虑机电波传播的前提下，扰动功率在同步机间瞬时分配［20］。在惯量响应阶段，同步机端电磁功率突变，而机械功率由于汽轮机的气门和水轮机水门来不及动作，机械功率不能突变，则电磁功率和机械功率的差值完全由存储在同步机转子中的旋转动能来承担，同步机的惯量支撑功率为：

式中：ΔPg为同步机的惯量支撑功率；dfg/dt为发电机母线频率变化率。

对于同步机，如果可以准确测量原动机施加在同步机转子上的机械功率、同步机端电磁功率和同步机母线的频率变化率，就可以准确感知扰动发生后同步机的惯量大小，有

对于采用虚拟惯量控制的CIG，在物理结构上不存在真实的原动机，并不具备机械功率输入。但是CIG 可以像同步机一样，在系统发生扰动的情况下发出有功功率支撑电网频率。CIG 的等效惯量支撑功率为：

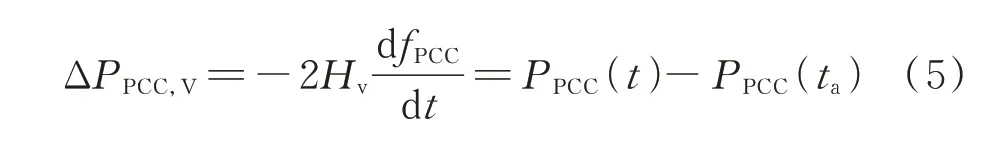
式中：ΔPPCC，V为并网点虚拟惯量控制增发有功功率的大小；PPCC(t)为t时刻CIG 并网点测量有功功率；ta为频率越过调频控制死区，触发CIG 调频的时刻；fPCC为CIG 并网点测量频率。需要说明的是，当系统频率跌落时，dfPCC/dt为负值，Hv通常设为正值，则需要在表达式前增加负号，以保证在频率事件中CIG 增发有功功率，支撑电网频率。

因此，在评价CIG 等效惯量时，应采用下式：

考虑CIG 内部调频资源响应速度和控制方式的不同，采用一种平均化的思想，评价其在一段时间内的平均作用，同时降低测量噪声和频率变化率测量误差对评估的影响。从能量的视角出发，设计评估算法：

式中：n为积分计算的时间窗长，该积分窗会随时序滑动；Ts为数据采样周期。n的取值不宜过小，太小将无法体现对噪声的平抑作用；n的取值也不宜过大，由于虚拟惯量作用时间有限，n值过大将造成评估结果偏低，反而增大误差。本文在采样周期为20 ms 的情况下，设置n为6。需要指出的是，本文提出的积分算法在一定程度上能够消除功率波动的影响，提高算法的精度。然而，由于积分窗长的影响，需要一定的数据量，对实时性略有影响。

2.2 CIG 一次调频系数估计与修正

频率扰动事件中，在时序上虚拟惯量与一次调频作用存在重合部分［21］。对于CIG 而言，在监测并网点有功功率时，并不能区别惯量支撑功率和一次调频功率，即在扰动事件中，当频率偏差越过一次调频死区时，并网点的实测有功增量为：

式中：ΔPPCC为CIG 并网点有功增量；Kv为CIG 一次调频下垂系数；f0为电网标准频率（50 Hz）。

此时，在Kv未知的情况下，依靠并网点频率和有功功率数据无法计算Hv的大小。本文基于一次调频和虚拟惯量控制馈入能量的特征差异，对一次调频系数进行估计。先计算Kv的大小，通过剥离并网点实测有功增量中的一次调频功率，获取虚拟惯量控制支撑功率的大小，有

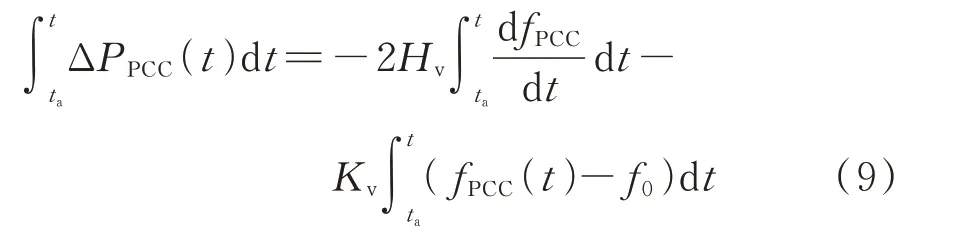
图1（a）所示为一次典型频率扰动中CIG 按照式（9）计算的虚拟惯量和一次调频支撑控制向系统馈入的能量，虚拟惯量参数和一次调频参数均采用典型值，Hv为4 s，Kv为25［22］。

图1 虚拟惯量与一次调频控制馈入能量Fig.1 Energy injected from virtual inertia and primary frequency regulation control

在扰动初期，并网点向电网馈入能量主要由虚拟惯量控制提供，这是因为扰动初期频率变化率（rate of change of frequency，RoCoF）较大，频率偏差较小。当一次调频投入后，随着频率偏差增大，RoCoF 减小，并网点馈入电网的能量主要由一次调频控制提供。如图1（b）所示，当t≥tf时，由于虚拟惯量控制的有功响应提供非常短时的功率支撑［21］，其长时间尺度的累积电量低于1%，造成一次调频系数估计误差低于1%，可近似忽略，则有：

由于扰动强度大小不同，tf大小也会不同。通过对有功增量和频率长时间尺度的积分，当计算结果|Kv(tn)-Kv(tn-1)|小于等于定值ε时，获得等效一次调频系数Kv，本文取ε=0.01。求解出Kv后，即可通过剥离一次调频控制增发的有功功率，计算虚拟惯量控制增发的有功功率：

2.3 CIG 有功响应延时估计与修正

2.3.1 延时产生的原因

同步机的惯量是本身具有的固有属性，扰动发生后同步机瞬时承担扰动功率，即同步机惯量响应不存在延时。调频模块响应时序如图2 所示。

图2 调频模块响应时序Fig.2 Response time sequence of frequency regulation module

如图2 所示，对于CIG，延时主要包含以下几个部分：

1）CIG 需要通过频率、频率变化率测量环节，采用锁相环锁相或利用同步相量测量单元（phasor measurement unit，PMU）测量频率、频率变化率，存在延时。

2）测量结果通过通信链路传递给控制器存在通信延时。

3）控制器计算并分配指令存在延时。

4）单体风机、光伏、储能模块所能提供有功支撑能力有限，实际应用中往往需要大规模集群利用，从而在控制形式上可能采用多级控制，例如：场站群-场站-单机。不同控制层级间控制指令传输需要时间。

5）单体风机、光伏、储能模块响应控制指令存在滞后时间。

对于跟网型虚拟惯量控制，延时环节包含上述5 个部分；对于构网型虚拟惯量控制，相比跟网型往往不包含第1）部分。对单体风机、光伏、储能模块调度方式的不同，延时的组成亦有所不同，例如采用多级调控方式的延时环节包含第3）和第4）部分。另外，受通信链路数据流量大小和通信距离长短的影响，指令传输时间可能浮动，存在不确定性。

上述延时会导致频率变化率输入和有功输出在时序上错位，造成调频模块输入输出的非线性。如果直接利用并网点实测频率和有功功率计算等效惯量，会降低评估结果的准确性。

2.3.2 延时估计与修正

现行规定中，为了保证设备的使用寿命，避免设备频繁动作，提高储能电站的安全性，通常对虚拟惯量和一次调频控制设置死区［23-24］。本文对风光储电站虚拟惯量控制设置死区±0.05 Hz，一次调频控制设置死区±0.05 Hz，符合国家标准规定。只有测量频率超过控制死区时，才会触发CIG 调频控制。为了方便说明算法的原理，本节以含风光储电站频率控制的某区域电网实时数字仿真（real-time digital simulation，RTDS）系统闭环仿真模型为例进行说明，模型详细说明将在第3 章给出。仿真设置该区域于6 s 时发生节点负荷突增50%的频率扰动故障，其中风光储场站只投入虚拟惯量控制，结果如图3 所示。

并网点测得频率如图3（a）所示。CIG 在扰动期间响应控制器发出第一个控制指令，上升至指令10%的时刻［23］记为tb，则待求延时为：

式中：Td为CIG 有功响应延时。

如图3（b）所示，虚线为控制器中有功指令，指令下达周期为500 ms。当并网点频率越过死区后，控制器没有在ta时刻发出指令，其指令存在一定延迟。在扰动期间，当控制器生成第一个指令后，调频模块经过一个时滞，才开始响应指令。

图3 延时估计原理Fig.3 Principle of time delay estimation

为了消除延时对评估带来的影响，需要设计一种算法，计算并消除延时，并保证有一定的抗干扰能力。本文利用CIG 并网点的频率数据获取ta，利用有功数据获取tb，最终计算并修正延时。

并网点测量频率偏差超过死区时，ta可以通过PMU 测量的带有时标的频率数据获得。PMU 对电气量的采样周期为20 ms，有

式中：f(ta)为ta时刻并网点测量频率值；Δfdb为CIG设定的虚拟惯量控制死区。

同时，计算CIG 进入调频控制前，正常运行时的有功功率运行点，即频率控制的基准功率，这里采用时刻ta前1 s 的有功数据取平均值。这样做之所以是合理的，一方面由于实测有功数据可能存在噪声，取平均值有利于平抑噪声；另一方面，CIG 内部用于提供有功功率的电源在1 s 内不会产生较大波动。则正常运行时CIG 的有功功率为：

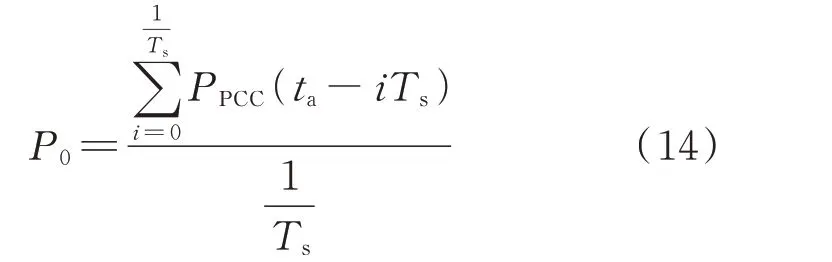
式中：P0为CIG 进入虚拟惯量控制前，正常运行时并网点测得的有功功率。

在时刻ta后，计算CIG 在扰动事件中有功功率的增量：

按照式（15）计算获得并网点处在扰动事件中的有功增量如图3（b）实线所示。为了降低有功测量白噪声、新能源电源的波动对延时计算的影响，对有功增量取积分处理：

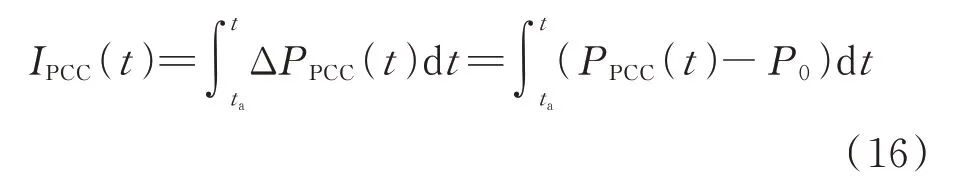
式中：IPCC(t)为有功增量的积分。

按照式（16）计算获得并网点处在扰动事件中的有功增量积分，如图3（c）所示，该积分随时间的推移而不断累积。

CIG 正向增发有功功率后，有功增量的积分在扰动初期呈现单调性。当CIG 有功运行点改变时，积分曲线的斜率发生变化，利用积分曲线斜率的差值判断CIG 是否响应虚拟惯量控制：

式中：RPCC(tn)为tn时刻积分曲线斜率的差值。

当相邻两点的积分曲线斜率的差值足够小，认为此时CIG 的运行状态未发生显著变化。当CIG运行状态改变时，并网点测得有功功率将发生变化，会导致有功增量的积分发生变化。为准确判断并网点有功变化是由虚拟惯量控制引起，提高算法自适应性、抗干扰能力及判断的可靠性，延时算法包含一个计数器和动态门槛值。动态门槛值计算：

式中：α为人为设定的定值；TPCC(tn)为tn时刻的动态门槛值。tn时刻的门槛值由前一时刻tn-1的积分曲线斜率决定，相比固定门槛值具有更强的自适应性。当RPCC(tn)高于门槛值TPCC(tn)时，计数器清零，否则进1。计数器设计如下：

式 中：β为0-1 变量；C为一无量纲量，初始值为0。当tn时刻满足β(tn)=1 时，C(tn)自动进1，否则C(tn)=0。

当C(t)超过计数器设定门槛值Cset时，认为CIG 的运行状态发生了改变，CIG 开始响应调频控制。图3（c）所示的积分曲线经式（17）至式（20）的处理后，结果如图3（d）所示。当C(tn)=Cset时，记该时刻为tc。自tc起，向前寻找计数器第1 个为零的时刻，即为tb。至此，可以获知CIG 响应调频控制的延时大小，即式（12）。

α反映了算法对有功变化的灵敏度。CIG 有功变化的大小则取决于调频模块有功响应爬坡率。有功响应爬坡率一方面取决于系统发生扰动造成频率偏移的大小，另一方面取决于调频模块自身的响应特性。因此，参数α应按照式（21）选取：

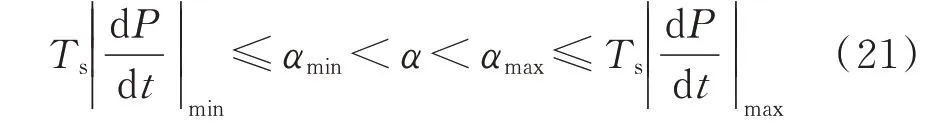
式 中：|dP/dt|min和|dP/dt|max分 别 为CIG 有 功 功 率变化率绝对值的最小值和最大值；αmin为参数α可取的最小值；αmax为参数α可取的最大值。

α越大，算法对有功功率变化的灵敏度越低，反之亦然。若α足够大，按照式（20）计算将判定CIG有功响应无延时。若α较小，由于并网点有功功率存在波动，测量环节存在白噪声，会干扰算法对有功功率变化的判断，降低延时计算的准确性。

Cset反映了并网点有功功率改变的持续时间，即调频控制的持续时间。由于不同扰动强度下，调频控制持续的时间长短不同，Cset不宜设置太高。

由前述分析可知，该延时的大小描述的是CIG有功响应相对频率的迟滞现象。所以，在评估CIG等效惯量时，应对实测有功数据进行延时修正，同时，将一次调频增发的有功功率剥离，有

2.4 CIG 等效惯量评估流程

计及功率响应延时补偿的换流器接口等效惯量评估整体流程如图4 所示。首先，基于PMU 测量CIG 并网点的节点频率和有功功率，通过节点频率数据是否超过CIG 虚拟惯量控制死区并保持100 ms，判断CIG 是否触发调频控制，并避免量测噪声和误差引发误评估。若判断CIG 触发调频控制，则触发CIG 的等效惯量评估。其次，计算CIG 投入虚拟惯量及一次调频控制后的有功增量，同时判断并网点的频率和有功功率数据量是否满足用于等效惯量计算的积分窗长。再次，通过长时间尺度的积分计算一次调频下垂系数，并计算CIG 的有功响应延时。最后，修正CIG 投入虚拟惯量控制后的有功增量并计算CIG 并网点的等效惯量。

图4 等效惯量估计算法流程图Fig.4 Flow chart of equivalent inertia estimation algorithm

3 仿真算例

为了验证所提方法的有效性，本文采用RTDS搭建含风光储电站的某区域电网模型，通过风光储电站频率控制器构建闭环实时仿真系统，对提出的等效惯量评估方法进行仿真验证。调频控制器中包含电气量测量算法以及调频控制算法，调频控制策略采用跟网型虚拟惯量及一次调频控制，以模拟实际工程应用场景。该区域电网结构如图5 所示，风光储电站接入CZ 节点，在系统正常运行的一个潮流断面下，该区域电网等值系统总容量为13 168 MV·A，总负荷为7 654.7 MW。

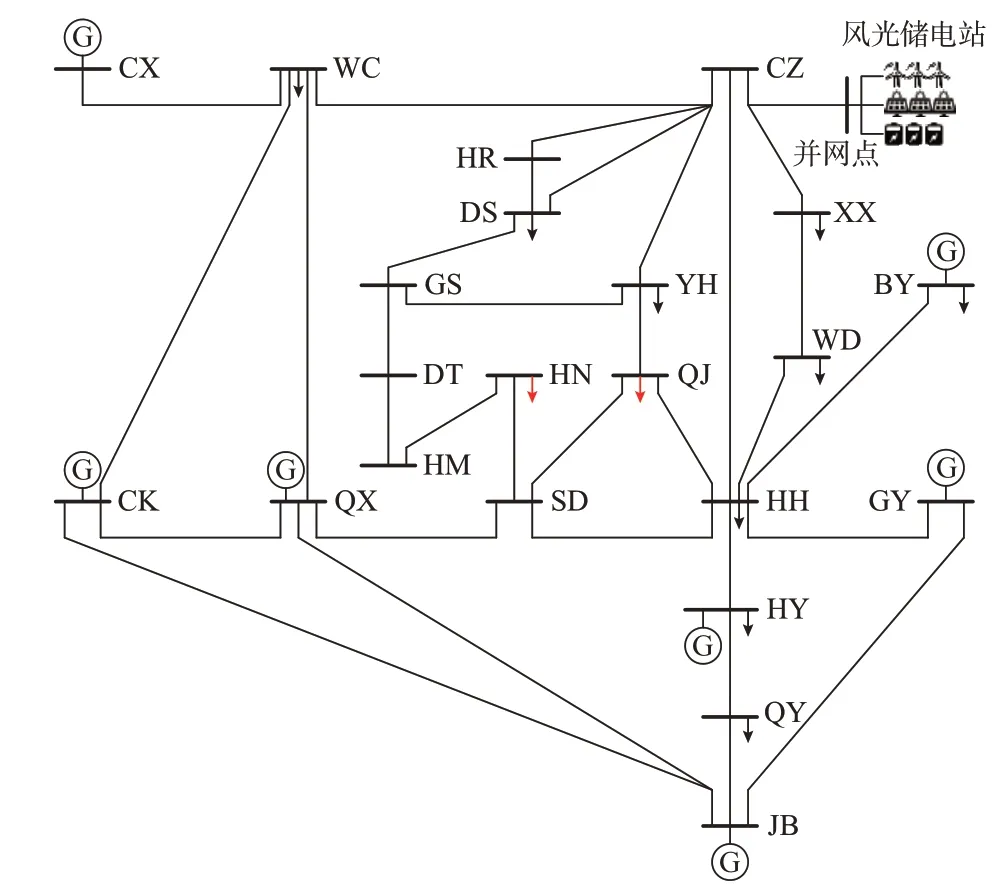
图5 某区域电网拓扑Fig.5 Topology of power grid in a certain area

风电机组采用双馈风电机组，容量为425 MW，光伏发电容量为75 MW，储能容量为140 MW/280 MW·h，均采用等值模型，信号采样周期为20 ms，以模拟工程现场并网点PMU 采集频率和有功数据。按照国家标准规定，对风电、光伏、储能虚拟惯量控制设置死区±0.05 Hz，一次调频控制设置死区±0.05 Hz［23-24］。

3.1 α 和Cset的选取与分析

在风光储电站不同资源参与调频的情况下，本文首先基于仿真模型在6 s 时HN 和QJ 节点分别发生80%、50%、25%负荷突增扰动，验证延时算法在系统发生不同强度扰动及调频模块不同响应速度情况下的准确性。案例如下：

案例1：HN、QJ 节点负荷突增50%，储能参与虚拟惯量及一次调频控制。

案例2：HN、QJ 节点负荷突增25%，储能参与虚拟惯量及一次调频控制。

案例3：HN、QJ 节点负荷突增50%，光储参与虚拟惯量及一次调频控制。

案例4：HN、QJ 节点负荷突增25%，光储参与虚拟惯量及一次调频控制。

案例5：HN、QJ 节点负荷突增80%，风光储参与虚拟惯量及一次调频控制。

案例6：HN、QJ 节点负荷突增50%，风光储参与虚拟惯量及一次调频控制。

案例7：HN、QJ 节点负荷突增25%，风光储参与虚拟惯量及一次调频控制。

不同算法参数计算延时的结果见附录A 表A1—表A3。附录A 中理论延时按照2.3.2 节中的分析计算获得，即式（12）。几种案例的理论延时有所不同，除了2.3.1 节分析的原因外，控制器的运算处理能力也将影响该延时的大小。

根据附录A 中的测试结果，当α取0.1～0.25时，提高算法对CIG 并网点有功变化的灵敏度，并网点有功波动及测量噪声将使算法产生误差；当α取1.25～1.5 时，降低算法对CIG 并网点有功变化的灵敏度，使算法无法计算延时。因此，α应在0.5～1.0 之间取值。实际工程中，PMU 对电气量的采样周期已知，有功功率变化率可以通过CIG 在不同工况下的阶跃实验获得［23］，即可根据式（21）选取合适的α值。根据附录A 测试结果，当Cset取10～25 时，若有功波动及测量噪声触及式（18）的门槛值，较低的Cset会降低算法判断有功功率变化的可靠性。本文测试场景下，CIG 调频控制作用时间较长，而实际工程中，不同扰动强度下调频控制持续的时间长短不同，因此Cset不宜设置过高。根据附录A 测试结果，为保证算法的可靠性，Cset应在50～200 之间取值。综合附录A 测试结果及上述分析，本文取α为0.5，Cset为100。

延时计算的准确度一方面取决于算法参数设置是否合适，另一方面取决于数据量测的准确度和数据的采样周期。由于本文采用20 ms 作为采样周期，延时计算结果为采样周期的整数倍。延时计算的准确度最终也将影响等效惯量评估的精度。

3.2 等效惯量评估结果与分析

在RTDS 模型中设置6 s 时系统在节点HN 和QJ 处分别突增负荷80%、50%、25%，测量并网点有功功率变化和节点频率变化，对风光储电站的等效惯量进行评估。分别在3.1 节中提及的7 种案例下验证所提方法的正确性。

在CIG 并网点测得的有功功率和频率曲线见附录B。利用扰动后数据计算得到风光储并网点等效一次调频系数如表1 所示。一次调频系数均以基准容量500 MV·A 来表示。计及功率响应延时补偿的等效惯量评估结果如表2 所示。

如 表1 和 表2 所 示，在 案 例1 至7 中，当 一 次 调频评估结果偏高时，惯量评估结果偏低。这是由于当并网点馈入电网有功功率一定时，计算一次调频系数偏高导致计算虚拟惯量有功功率偏低。

表1 一次调频估计结果Table 1 Estimation results for primary frequency regulation

表2 等效惯量估计结果Table 2 Estimation results of equivalent inertia

在案例1 至7 中，评估结果均出现偏差，这是由于：1）非受控调频模块在调频模块参与调频控制的过程中，产生正向或负向的有功功率波动，造成并网点有功功率出现波动，进而影响评估结果；2）如图3（b）所示，受控调频模块在响应有功指令时存在偏差。例如在案例4 中，一次调频和惯量评估结果均出现较大的偏差，这是由于此时风电的功率出现较大的正向有功波动，导致并网点除了光伏和储能提供的调频支撑功率外，还有风电的功率波动增量，使得一次调频评估结果偏高，而等效惯量评估结果偏低。由于调频模块功率波动造成并网点评估偏差，不能视为误差。这是因为调频控制本质是通过调频模块增发有功功率，使得系统有功功率平衡，从而使得频率稳定。对于负荷突增的扰动情况，正向的有功波动增量有利于有功平衡，计算得到的一次调频系数偏高反映了这种特性。因此，本文所提方法适用于CIG 的等效惯量评估。

4 结语

本文提出了一种计及功率响应延时补偿的换流器接口等效惯量评估方法。根据CIG 并网点的节点频率，判断CIG 是否投入虚拟惯量控制。在此基础上，通过对节点有功增量长时间尺度的积分计算一次调频下垂系数Kv并计算延时Td，消除一次调频功率和有功响应延时对等效惯量评估的影响。最终对CIG 的等效惯量进行评估，通过RTDS 和实际频率控制器构建闭环实时仿真系统验证了方法的正确性，主要结论如下：

1）所提计及功率响应延时补偿的换流器接口等效惯量评估方法，基于PMU 的量测数据，从并网点外特性的角度出发对CIG 进行等效惯量评估。所提方法仅需测量CIG 并网点节点频率和有功功率，所需量测量少，计算复杂度低，便于实现在线监测。

2）所提延时计算方法，α的取值范围在0.5～1.0、Cset在50～200 时，能够保证所提算法对噪声和干扰的耐受能力，并保证延时计算方法的精度。经仿真验证，本文所提延时计算方法精度较高。由于实验室噪声环境与工程现场不同，以及PMU 量测数据受内置算法的影响，在工程应用中延时算法参数取值应灵活设定。

随着新能源的大量接入，系统惯量水平下降，新能源主动支撑系统频率的能力愈发重要。因此，准确评价CIG 等效惯量，对指导和规划新能源并网，保证双高电力系统的频率稳定非常重要。如何在系统正常运行情况下评价CIG 等效惯量，同时根据等效惯量评估的结果来修正CIG 调频控制的关键参数以及优化调频资源的分配是下一步研究的重点。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。