刚性轮径向受力分布分析测量
闫旭光 赵正旭 卢石磊
青岛理工大学 山东 青岛 266520
引言
月球昼夜温差可达300℃,月表环境复杂恶劣[1],成熟的橡胶轮胎技术因高真空、微重力、强辐射等因素无法移植应用到月球探索当中。探月车车轮在能支撑车体质量的前提下,应更加注重轻便可靠,月球车等太空探索移动装备通常使用镂空的金属骨架结构,保证稳定性,而刚性轮是高度进化的高效骨架结构,刚性轮没有轮胎,主要由轮毂、轮辐和轮辋组成。月球遍布碎石和环形山,行驶条件严苛,在没有轮胎缓冲的工况下,刚性轮行驶过程中,容易形成应力集中造成整体性结构破坏。因此有必要研究刚性轮结构从轮心到轮缘的径向受力分布,根据轮心与轮缘之间径向作用力分布情况,重新设置轮毂结构,不但可以使得车轮更加轻便,还可以使得刚性轮即使局部出现缺损,但车轮整体结构相对完整的情况下,继续完成任务,具有更高的可靠性。
我国玉兔号月球车采用钛合金轮辐与轮缘一体式筛网轮结构,结构简单质量轻,但在冲击载荷作用下,易发生变形损坏,不适合崎岖路面行驶。
国内目前对刚性轮结构径向受力分析研究较为缺乏,可参考其他类似结构的受力分析。宋涛[2]根据轮辐索结构传力特点,引入连续化方法,求解得到了结构内力和位移的近似解析解。罗孟杰[3]详细介绍了自行车车轮和辐条的电测实验应力分析的方法及所测得的车轮和辐条的应力分布情况,为理论分析奠定基础。庄锦华等人[4]在罗的基础上对车轮辐条的受力进行理论分析,导出了计算车轮辐条内力,应力确定辐条予紧张力,以及设计采用辐条直径的通用公式。最近,Ravivat Rugsaj和Chakrit Suvanjumrat[5]则通过有限元分析超弹性三维模型来确定径向辐条最大局部应力,而Zifeng Zhang和Hongxun Fu[6]等人,仿真不同载荷作用下轮胎的径向窒息度,根据袋鼠下肢结构特点改进径向结构,设计研制了一种仿生柔性辐条,为轮状结构研究提供了新的理论和方法论。
1 实验
1.1 力学分析方法
刚性轮主要受到三种载荷:飞轮给花鼓的驱动力载荷、承重载荷以及阻力载荷。三种载荷在理论力学以及材料力学的限定条件下,是线性叠加的关系,即每个载荷所带来的影响可以独立分析。本文仅以承重载荷作为研究对象,在理论力学和材料力学范畴内分析在承重载荷的作用下,各个辐条内部张力的变化。
该分析为得到承重载荷与刚性轮径向受力分布之间的相互关系,为后续研究奠定基础,更好地探究应力分布情况,进而与传感器结合改进特殊应用场景下的轮状结构。
辐条根据其工作原理以及压杆临界条件判断为只承受拉
如图1所示,该刚性轮为最基本的直拉无偏编法,称重载荷为P,共有n根辐条等分车轮,编号为i的辐条与1号辐条夹角为αi,所受力为,该系统为平面汇交力系,并构成拉压超静定杆系且符合胡克定律,如图2所示,则有:
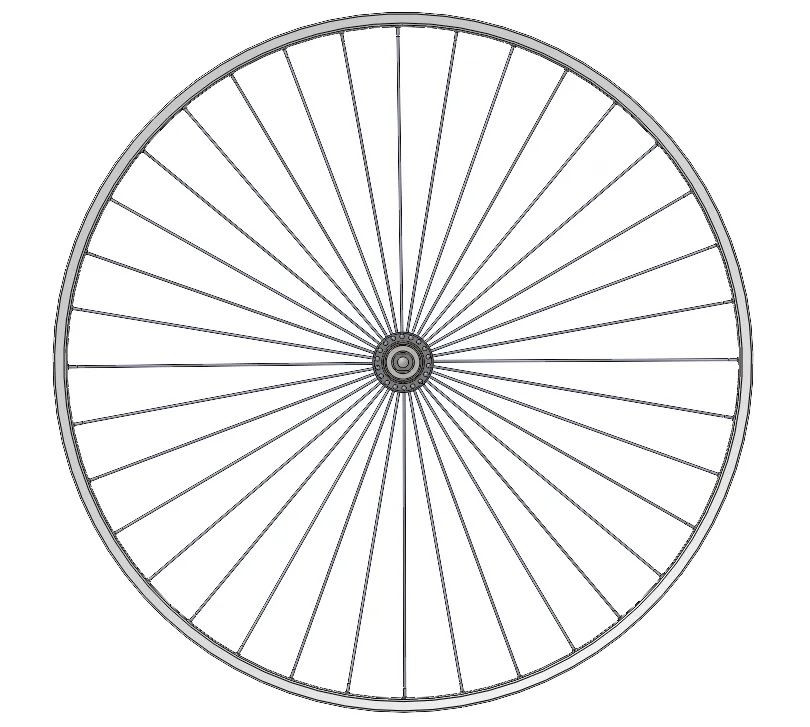
图1 承重载荷下X0无偏刚性轮受力情况
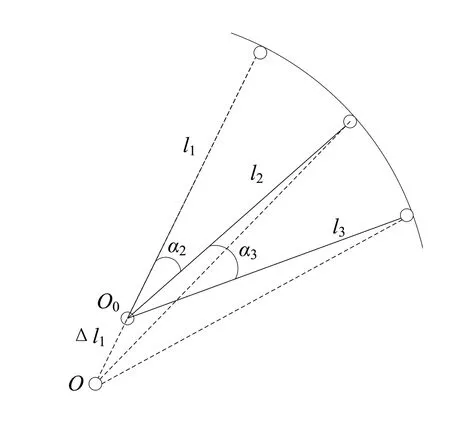
图2 变形协调理论
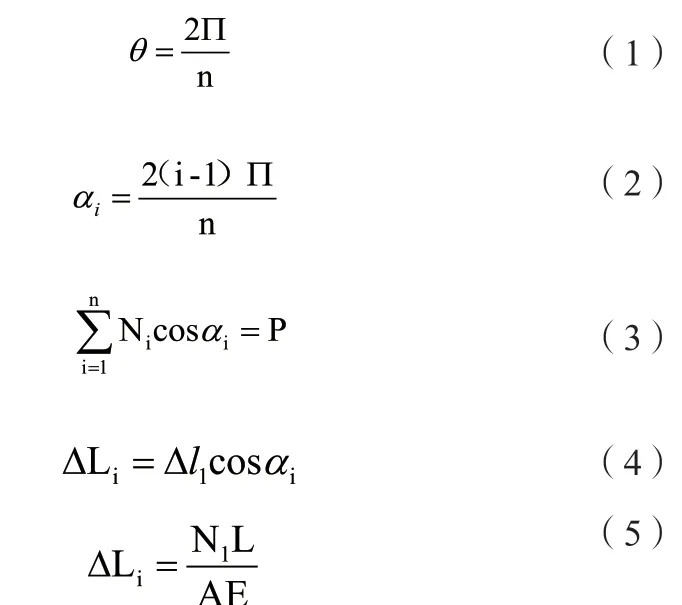
其中:
L-辐条原长;
A-截面积;
E-弹性模量。力,将刚性轮上部居中的辐条定义为1号辐条之后顺时针依次编号。
由上述方程组(1)~(5),可解得,均为拉力:

上述计算过程中,将实际情况中的预紧力省略,因此实际所受的力为:
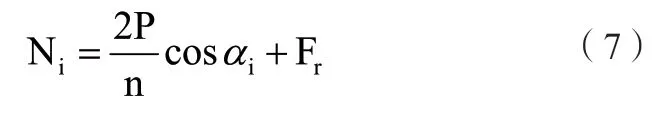
以X1为例说明交叉偏心编法的数学模型求解方法,用表示考虑偏心的情况的受力,如图3所示,β1和β2分别为非驱动侧和驱动侧的夹角则有:
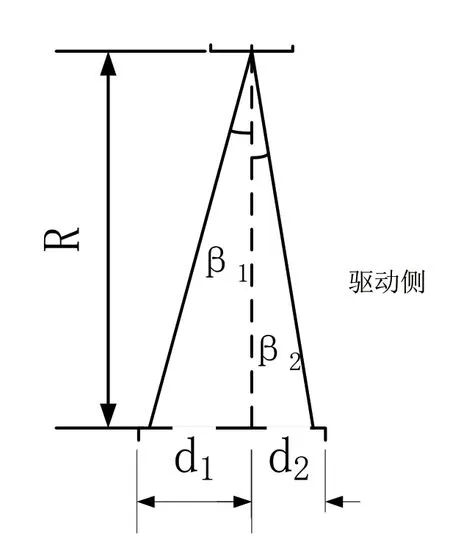
图3 驱动侧和非驱动侧偏心示意
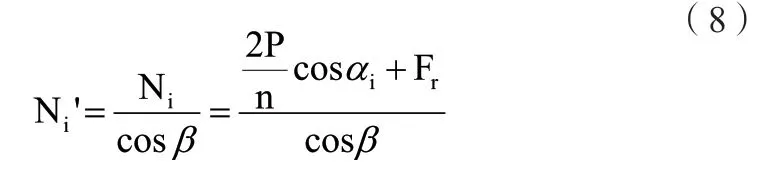
图4为同一根辐条X1编法(实线)与X0编法(虚线)的位置关系,夹角为φ,用代表X1编法辐条受力,则有:
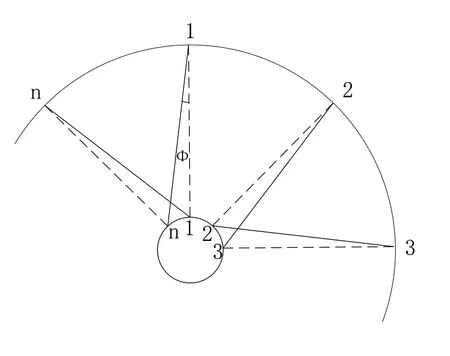
图4 以X1为例的交叉编法偏转角度
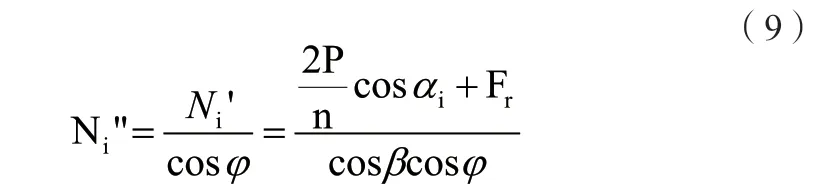
1.2 建立正交实验
在本研究中,设计正交实验,选取比较了放射(X0)和交叉(X3)两种辐条编法、24和36两种辐条数量,两个参数对辐条受力分布的影响情况。

表1 正交实验表
根据1.1介绍方法,X3编法刚性轮受力分布公式为:
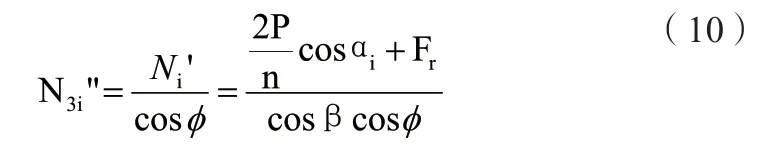
实测得数据如表2所示:
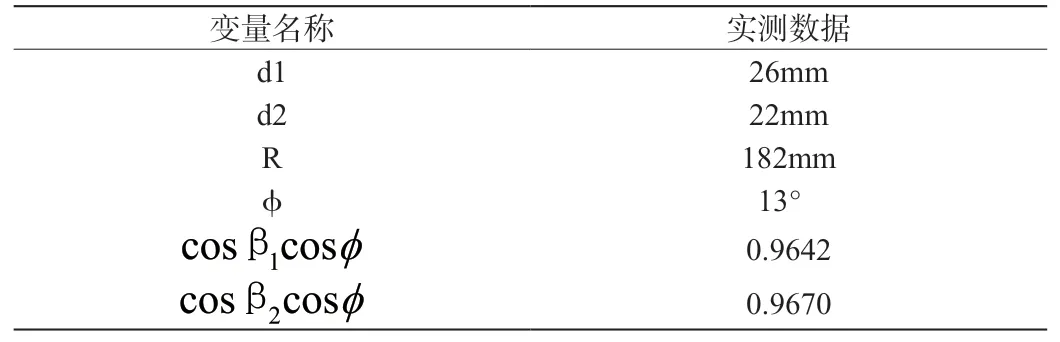
表2 待试车轮参数实测表
图5表示的是(编法-辐条数)X0-24、X0-36、X3-24和X3-36刚性轮,在1000N的承重载荷作用下利用数学模型推算求解的各辐条受力情况,为让张力变化更加明显,将预紧力设定为100N:

图5 1000N承重载荷下刚性轮受力分布图

计算可得,在100N预紧力、1000N承重载荷作用下:如图5(a),X0-24刚性轮1号辐条张力最大,为183.333N,13号辐条张力最小,为16.667N,7号辐条和19号辐条张力仍等于预紧力100N;如图5(b),X0-36刚性轮1号辐条张力最大,为155.556N,19号辐条张力最小,为44.444N,10号辐条和28号辐条张力仍等于预紧力100N;如图5(c),X3-24刚性轮1号辐条张力最大,为176.587N,13号辐条张力最小,为16.053N;如图5(d),X3-36刚性轮1号辐条张力最大,为149.987N,19号辐条张力最小,为42.853N。
图6展示的是正交实验结果对比图,如图6(a)所示, 横坐标1-24代表辐条编号,纵坐标0-200代表张力力值(单位N),红色曲线代表X0-24的刚性轮受力分布,蓝色曲线代表X3-24的刚性轮受力分布,如图6(b)所示,横坐标代表辐条编号,纵坐标代表张力力值(单位N),红色曲线代表X3-36的刚性轮受力分布,蓝色曲线代表X0-36的刚性轮受力分布,通过图6(a)(b),可以看出相同辐条数,放射编法X0辐条张力最大值明显大于交叉编法X3最大值,而两种编法最小值相差无几。
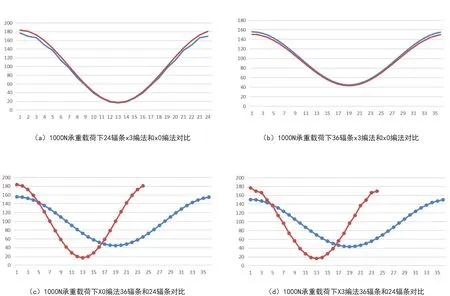
图6 1000N承重载荷下刚性轮受力分布对比图
图6(c)所示,横坐标代表辐条编号,纵坐标代表张力力值(单位N),红色曲线代表X0-24刚性轮受力分布,蓝色曲线代表X0-36刚性轮受力分布,如图6(d)所示,横坐标代表辐条编号,纵坐标代表张力力值(单位N),红色曲线代表X3-24刚性轮受力分布,蓝色曲线代表X3-36刚性轮受力分布,通过图6(c)(d),可以发现相同编法条件下,辐条数量24的刚性轮辐条张力最大值明显大于辐条数量为36的刚性轮,辐条张力最小值也明显小于辐条数量为36的刚性轮,辐条数量较少的(以24根辐条为例)刚性轮曲线陡峭,辐条张力对载荷敏感,变化明显,而辐条数量较多的(以36根辐条为例)刚性轮曲线较为和缓,辐条张力对载荷较为迟钝,变化较为平稳。
1.3 搭建平台实验
搭建实验平台为刚性轮径向加载,选取X3-36的刚性轮作为实验对象,检测获取的各辐条受力情况,与数学模型计算结果进行定性对比分析。
如图7所示:1为底座板,2为螺杆,3为施力结构千斤顶的示意图,4为导向板,5为传感器,6为待测刚性轮,7为止挡板。实验用刚性轮参数如表3所示。
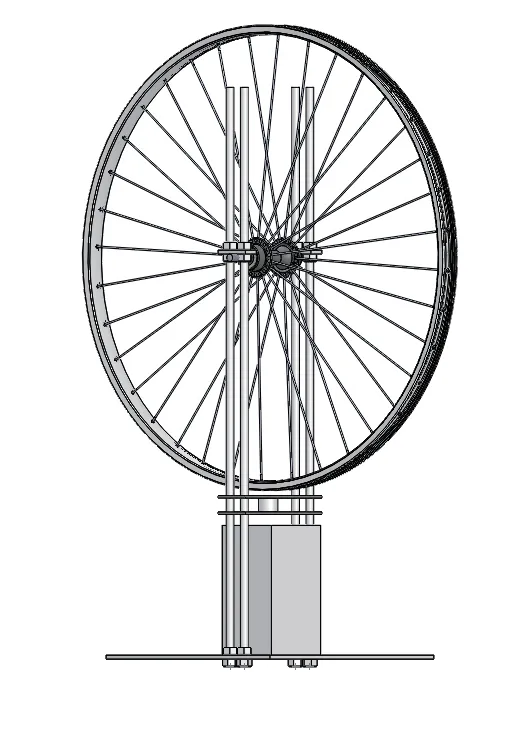
图7 刚性轮径向加载实验平台

表3 待测刚性轮参数
实验中刚性轮定义为刚体,用固定路面(止挡板)、对轮辋中心施加径向100KGN(约为1000N)载荷的方法来模拟车轮承重工况。
径向加载实验部分结果如图8所示:
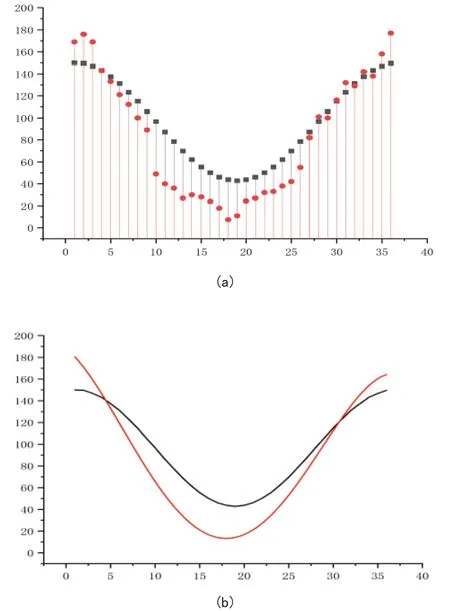
图8 实验结果与模拟计算结果对比
图8红色线为实验测试结果数据(实验值),黑色线为模拟计算结果(理论值),其中图8(b)红色曲线为四阶多项式拟合曲线。通过对比实验结果与计算结果,当辐条预紧力足够大的时候,刚性轮整体刚性增加,对承重载荷并不敏感,当辐条预紧力较小的时候,刚性轮整体刚性较差,各个位置的辐条对承重载荷更加敏感,受力变化分布更加明显。变化趋势与理论计算结果基本一致,均为上部拉应力变大,下半部拉应力变小。
2 结束语
①根据理论力学和材料力学建立了刚性轮上辐条受力分布的数学分析方法;②建立正交实验,使用该方法分析了4种刚性轮结构,分析结果认为辐条数较多、交叉数较多的刚性轮对承重载荷敏感度较低,且受力分布更加均匀。③搭建了实验平台,检测了在受到较小预紧力条件下不同位置辐条的受力分布情况,实验结果与数学演算结果趋势一致,验证了该数学模型的合理性,可以改进使其更加符合实际情况,运用于后续研究。④本文只考虑了承重载荷在小预紧力的特殊条件下的作用效果,在接下来的研究中,将会更加贴合实际情况,将制动力、阻力、驱动力等载荷加入,不再仅限于预紧力较小的情况,实验设计更加合理,更加符合实际情况。

