集合、同化思想在大气科学中的渗透

薛建军 贾朋群 肖子牛

（1 中国气象局气象干部培训学院，北京 100081； 2 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室，北京 100029）

0 引言

大气科学作为一门较新的应用性学科，它的学科独立、迅速发展与数学、物理、化学等学科的发展和相关技术的进步密不可分。自18世纪中叶以来，在几次科技革命的推动下，大气科学从定性描述到定量分析再到预报预测能力的日臻成熟[1-3]。特别是进入20世纪50年代以来，伴随着数值预报概念的提出到其科学理论和技术方法的持续发展完善，大气科学取得了迅猛发展。作为大气科学发展的重要标志，数值预报早已引发了一场“静悄悄的革命”[4]，它的巨大成功和飞速进步无疑是建立在多年稳步持续的科学认知和技术进步的积累之上[4-5]，这其中就包括集合、同化的科学理论及其技术方法在大气科学中的渗透和应用。

1963年，Lorenz提出了著名的混沌理论，指出混沌系统由精确的确定性演化方程控制，但具有不可预测且看似随机的行为[6-8]。而大气、海洋等具有很强的混沌特性，导致预报预测时对初始状态具有高度的敏感性。众所周知，从数值预报建立的科学理论与技术基础上看，首先数值模式并不“完美”①即便模式“完美”，由于初值的误差及混沌特征，预报预测仍然不可避免地存在预报误差。，其次一个真实的物理系统的状态也无法准确测量。加之大气、海洋等因观测误差、分析误差、站网分布不均等原因都会导致误差不可避免[9]。因此，模式误差、初始误差以及非线性系统的不稳定性共同导致了大气、海洋及其耦合系统预报预测的不确定[10-13]。因此，为了尽可能地减小预报预测的误差，集合预报、资料同化的科学理论与技术方法“应需而生”并得以在现代天气气候预报预测中不断发展应用。

1 集合预报

1.1 集合预报的提出

通常认为集合预报的思想是由Epstein和Leith提出的[8-12,14-15]。在假定模式完美的情况下，找到一组合适的扰动，以“初值+扰动”进行预报来反映初值引起预报结果的不确定性，再通过集合平均保留各个预报最可能的共同结果，以减少初值带来的不确定性影响。在理论上可以用一个概率密度函数来描述这种不确定性[13,16]，Epstein提出显式积分Liouville方程估计大气状态的概率密度分布，但在实际中几乎难以实现。随后，Leith建议采用蒙特卡洛（Monte Carlo Forecasting，MCF）方法，用随机函数产生扰动形成的初始场，实现了集合预报从理论迈向实际[10,16-18]。

1.2 集合预报的发展

从时间上划分，一般可以将集合预报的发展历程划分为以下3个阶段[11-12,17]。第一阶段，20世纪70—80年代，主要开展集合预报理论方法研究和数值试验探索。第二阶段，20世纪90年代，随着计算机技术，特别是大规模高性能计算能力的提升，业务集合预报系统得以建立和发展。1992年12月7日，美国国家环境预报中心（NCEP）率先开展集合预报业务[19]，同年12月19日欧洲中期天气预报中心（ECMWF）的集合预报系统开始准业务运行并于18个月后（1994年5月）正式投入业务运行[19-20]。随后法国、英国、日本、澳大利亚、加拿大等国也建立了各自的集合预报系统[9,11-12,19]。第三阶段，20世纪90年代末以来，集合预报的研究更加深入，从初值的不确定性研究扩展到模式不确定性、集合预报产品解释应用技术等多个领域。集合预报迅速成为数值天气预报业务的核心，被全球多个国家和地区的业务、科研机构所采用，甚至成为全球各大气象强国竞相发展的重要领域之一。表1、表2分别给出了世界气象组织（WMO）数值试验工作组对集合预报业务现状及发展态势的最新调查[21]，可以看到，国外主要的业务中心仍然在持续加紧其在全球或区域集合预报的工作部署和技术研发。

表2 国外主要预报中心区域集合预报业务系统主要参数：水平分辨率（谱/格点）、垂直层数（L）、成员数（M）、预报时长及每天运行次数[21] Table2 Operational system parameters of the regional ensemble forecast of major forecast centers abroad: horizontal resolution (spectrum/grid), number of vertical layers (L), forecast duration, number of members (M), forecast duration and daily operation times

尽管我国的数值预报业务起步于1950年代并很快取得了一些具有国际影响的进展[22-24]，但直到改革开放之后，相关研究和业务应用才迎来了新的契机[24]。受限于计算资源等客观条件限制，国家气象中心在20世纪90年代中期引入新的高性能计算机后，于1996年5月开发建立了一套中期集合数值预报系统[11,13]。此后，1998年6月在国产神威巨型计算机上建立了T106L19全球模式的中期数值天气集合预报系统，并于2001年3月实现业务运行[16]。世纪之交，在数值预报以引进为主转为自主开发为主的大背景下，开启了我国新一代数值天气预报系统研发的新征程。经过多年努力，我国自主研发的国家级全球（CMA-GEPS）和区域集合预报系统得以建立（CMA-REPS）[13,24]，实现了全球50 km，15 d，中国区域10 km，3.5 d的集合预报。同时，基于中国气象局次季节−季节−年际尺度一体化气候模式预测系统（CMA-CPS）构建了第三代气候集合预测模式业务系统，实现大气45 km，海洋0.25°×0.25°的S2S（0～60 d）和季节（未来13个月）气候预测[25-26]（表3）。

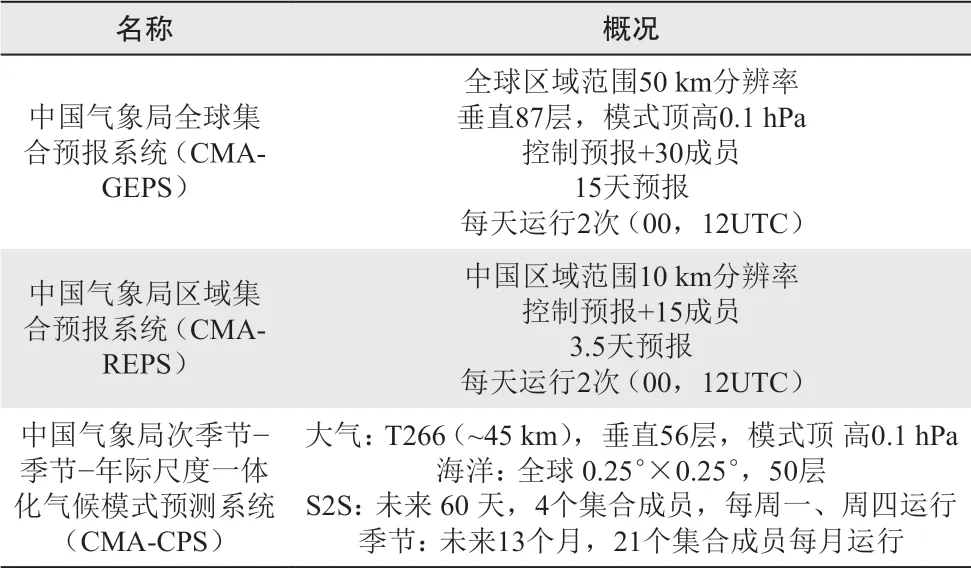
表3 国家级集合数值预报系统概况[25,26] Table 3 Overview of CMA Ensemble Numerical Weather Prediction System [25,26]

1.3 集合预报主要的技术方法

集合方法提出的背后，是考虑到“单一”的初值/模式的不确定性难以避免，而“一组”考虑了不同的初值/模式的不确定性影响得到的“一群”预报结果，其大概率是要好于某单个结果。简单归纳起来，集合预报的主要技术路线的思想如下[8-12,27-28]：

（1）假定模式完美，主要解决初值带来的不确定性影响。“初值问题”的解决是集合预报提出并得以建立起来的重要标志。通过“初值扰动”，生成一组不同考虑了不确定性的初值样本来驱动模式，得到集合预报结果。由于早期的蒙特卡洛法（MCF）、时间滞后平均（LAF）等方法存在较大的不足，难以满足实际业务应用需求[10,16-18,32]，实践中常用的方法有：[8-12,16-18,28-31]奇异向量法（SVs）、繁殖向量法（BVs）、观测扰动方法（PO）、集合转换（ET）和重新尺度化集合转换（ETR）和条件非线性最优扰动（CNOP）等。近年来集合卡尔曼滤波（EnKF）、集合转换卡尔曼滤波（ETKF）等数据同化的办法也有较多的应用。以上各方法特点及应用情况见表4。

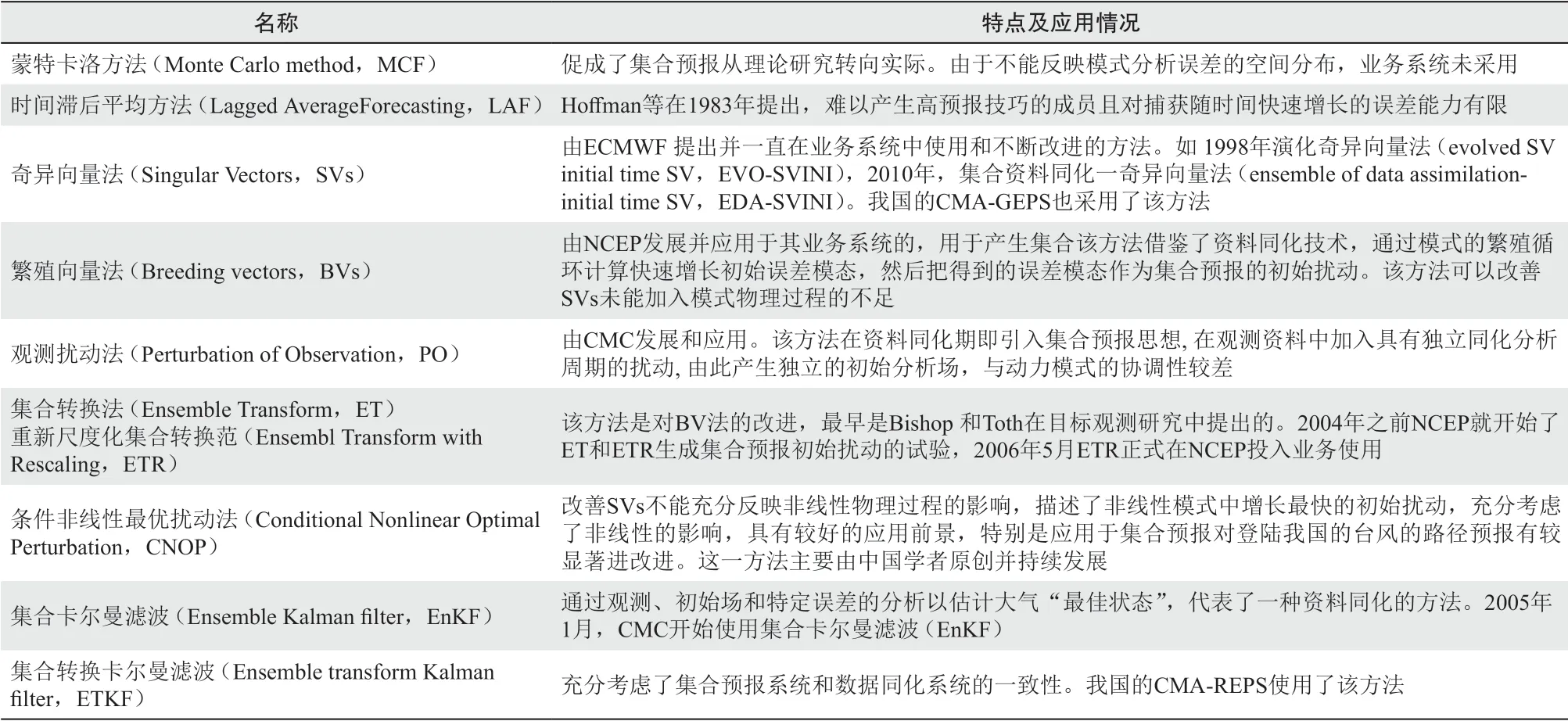
表4 集合预报初值扰动的主要方法及其应用情况[8-12, 16-18, 28-31] Table 4 Methods and applications of initial disturbance for ensemble forecasting [8-12, 16-18, 28-31]

（2）假定初值精确，致力于解决模式引起的不确定性影响。随着观测和同化等技术快速发展，一些研究认为模式系统误差也是影响天气集合预报效果的主要原因，比如模式中不同物理、化学过程、参数化方案等同样存在不确性。集合预报从仅考虑初值扩展到了考虑模式不确定性的影响[10,17,28-29,32]。具体的方法有：

多物理过程法。如加拿大气象中心（CMC）的全球集合预报系统采用多物理过程组合来减小物理过程不确定性引起的模式误差。如使用不同的对流、水平扩散、重力波拖曳、辐射和地形处理方案等[29,33]。

随机物理过程法。在集合预报系统中的模式倾向方程引入了随机物理过程法，该方法假定模式的不确定性主要来自于参数化过程的不准确和数值模式的截断误差。如ECMWF在1998年10着手考虑随机参数化扰动方案（SPPT），2010年11月引入随机补偿方案（SPBS）[10,20,29]。我国的CMA-GEPS、CMA-REPS和CMA-CPS目前也采用了SPPT方案[13,24,26]。

多模式集合。考虑了不同模式误差的综合影响，除了天气预报，多模式集合预报方法也被应用于气候预测的集合预报中，并取得了一定的成功[10]。

然而，由于模式误差往往与初始误差导致的预报误差相互作用难以区分，加之模式误差来源广泛，从次网格物理过程的参数化、模式离散到计算误差都有可能且相互耦合，对集合预报模式不确定性的改善比对初值引起的误差难度更大。

（3）模式和初值都不够好，设法同时解决两者带来的不确定性影响。除了单独考虑初值误差或模式误差，理论上也可将两者同时考虑解决。比如：

多模式−多初值集合法，同时考虑不同物理过程和初值不确定性对集合预报的影响，但可能在统计上不显著，预报成员之间存在较大的差异造成集合预报结果较大的系统偏差[8,10,12]。

随机全倾向扰动法（STTP）在数值模式倾向方程叠加随机强迫扰动，通过多次实现该随机扰动产生集合成员进行集合预报。NCEP从2010年开始使用此方法[10,29]。

1.4 ECMWF的集合预报

ECMWF作为最早开始发布业务集合预报的预报中心之一，经过近30年的发展，其集合预报技术和产品性能早已处在全球领先地位（图1）。从1992年以来，水平分辨率提升了20倍，从~320 km增加到~16 km；垂直分辨率提升了7倍，从19层增加到137层；预测时间从10 d延长到了46 d；集合成员个数从33个增加到51个；集合预报制作的频率也有所增加，当前还开展集合预报回报业务[20,34]。2021年5月11日，在ECMWF对其IFS（Integrated Forecasting System）进行的系统升级中（IFS Cycle 47r2），将模式计算由传统的双精度（64位浮点计算）降低至单精度（32位浮点计算）以节省计算资源，提高处理速度（图2），将集合预报从91层的垂直分辨率提至137层，实现其全球模式确定性预报（HRES）、数据同化（EDA）和集合预报（ENS）达到统一的垂直分层。测试结果显示，升级后的集合预报系统对自由大气整体的预报技巧提高了0.5%～2%，对50 hPa的平流层温度预报技巧提高了5%～20%，对热带对流层的预报技巧提高了6%。此外还提升了对热带气旋的预报技巧[35]。未来，ECMWF还将在2023年第一季度的Cycle 48r1计划中，将ENS的水平分辨率提升至9 km，以与HRES保持一致。同时将当前ENS extended作为一个单独的系统独立出来，维持36 km的水平分辨率和垂直137层的设置，以100成员每天从00 UTC运行到第46天[36]。这些改变无疑将加快ECMWF向“无缝的集合数据同化和预测系统”[37]迈出更加坚实地步伐。

图1 1995—2017年ECMWF北半球500 hPa位势高度集合预报CRPSS随时间的演变，预报时间为24 h、72 h、120 h、168 h和240 h（整体呈上升趋势，每条线上波动与季节相关的可预报性有关，冬季比夏季更容易预测）[20] Fig. 1 Time evolution, from 1995 to 2017, of the CRPSS of ENS forecasts for 500 hPa geopotential height over the Northern Hemisphere, for lead times of 24,72,120 168 and 240 hours. (The more or less regular pattern of peaks and troughs in each line stems from differences in predictability related to the seasons: winter weather tends to be more predictable than summer weather) [20]

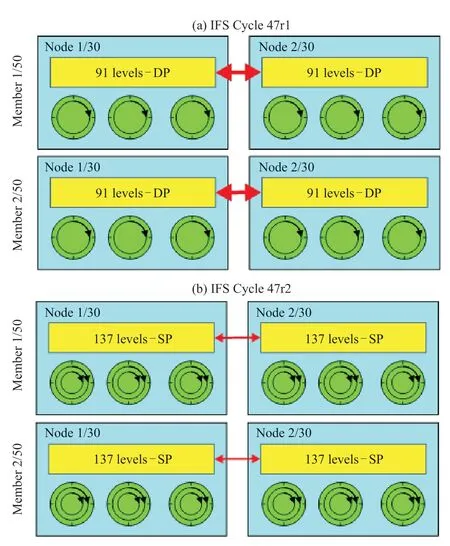
图2 IFS Cycle 47r1双精度（DP）和91层集合预测（a）与IFS Cycle 47r2单精度（SP）和137层集合预报（b）的计算效率比较（单精度更快（绿色圆圈）并且减少了每个节点（黄色框）内存之间的数据传输（红色箭头））[35] Fig. 2 The computational change from (a) IFS Cycle 47r1 with double precision (DP) and 91 levels in the ensemble forecast to (b) IFS Cycle 47r2 with single precision (SP) and 137 levels in the ensemble forecast allows faster core processing (green circles) and reduced data transfer (red arrows) between the memory on each node (yellow boxes)[35]

2 资料同化

2.1 资料同化的概念及其理论发展

初值问题是数值预报的核心问题之一，在给定初值的条件下通过既定的模式进行数值求解以得到未来时刻的预报结果[17,38-39]。资料同化是有效的初值形成方法，它能够“使用所有可用的信息，尽可能准确地估计大气运动的状态”[39-41]。先进的资料同化技术被认为是数值天气预报突破的关键因素之一[4,17,42-43]。资料同化通常包括资料预处理、客观分析和初始化等步骤，随着同化技术的不断发展，例如三/四维变分的应用，这些过程的界限越来越模糊，在实际中各步骤的功能已逐渐融合应用[17,43]。

同数值预报其他技术分支类似，资料同理论及方法也是在实践中伴随着数值模式、综合观测和高性能计算等技术进步而不断发展。早在1922年Richadson把观测资料手工插值到网格点上作为数值预报的初始场。20世纪50年代Charney、顾震潮等采用主观分析方法确定初值，这些也被看作是将同化的思想用于数值天气预报的主观分析中[39,44]。20世纪50年代随着计算机和数值模式的发展，逐渐发展了气象领域中的客观分析方法（OA），而大气资料同化就源于数值天气预报的客观分析方法。60年代随着初始方程预报模式的出现，初值中不同变量间的动力学平衡成为关注的问题，客观分析所需的背景场亦可由模式预报提供，构成了预报—观测—预报的循环，资料同化的完整概念形成，并发展了统计插值（又称最优插值）的客观分析。70年代初伴随着全球模式的出现，提出了基于全球大气基本运动模态的非线性正规模式初始化方案。80年代以后资料同化的理论框架逐渐建立起来，这一时期卫星遥感资料的应用也极大地推动了同化理论与方法的研究。80年代后期提出的变分同化方法，90年代中期又提出了基于集合预报的卡尔曼滤波方法等[17]。目前，三/四维变分、混合变分、集合资料同化等方法已广泛用于业务资料同化系统[24,42-43]，全球主要业务中心也一直将资料同化系统的研发和升级作为关键核心业务能力之一（表5）[21]。

表5 国外主要预报中心全球资料同化系统主要参数：同化类型、水平分辨率（谱/格点）、垂直层数（L）、成员数（M）[21] Table 5 2 Operational system parameters of the global data assimilation system of major forecast centers abroad: assimilation type, horizontal resolution (spectrum/grid point), vertical layer number (L), and number of members (M) [21]

2.2 资料同化的方法

现代气象业务中资料分析同化的基本方法大致经历了以下发展[39-40,42-44]。多项式函数拟合方法，由Panofskyu 1949年提出[45]，是比较早的客观分析方法。逐步订正方法（Successive Correction Method，SCM），Bergthorsson等[46]，Cressman[47]将它发展为一个业务客观分析方案，用于美国当时的联合数值天气预报。最优插值方法（Optimal Interpolation，OI），经Gandin[48]全面地研制和开发，并应用到苏联的客观分析中。变分方法（Variational methods，Var）如3DVar/4DVar是国际上大多数主要业务数值预报中心正在使用或使用过的业务方案[49-50]。集合卡尔曼滤波法（Ensemble Kalman Filter，EnKF）在1994年由海洋学者Evensen[44]引入到资料同化领域，逐渐成为同化技术发展的热点[17,43]。

近年来，中国科学家也在资料同化方法研究中已取得了一些代表性成果[24]，如Wang 等[51]提出的降维投影四维变分同化（DRP-4DVar），Tian等[52]提出的集合四维变分同化方法（NLS-En4DVar）。此外，在业务同化系统中Han等[53-54]发展的有约束的卫星资料偏差订正技术（CBC，Constrained Bias Correction）作为重要的原创技术在CMA-GFS中取得显著成效，并被 ECMWF的同化系统引进和发展。尽管同化理论和技术方法也早已“今非昔比”取得了巨大进步，但在数值预报业务中的资料同化仍然面临一些问题，比如观测算子、偏差、误差、代表性、稀疏化、背景误差协方差、强/弱约束、伴随问题等交织在观测、同化框架和模式约束等多个方面[55]。对这些问题的持续改善也期待着新的技术方法的出现和成熟应用。

2.3 ECMWF资料同化新方向

ECMWF作为全球领先的气象中心，也是资料同化方面的技术研发和业务应用的佼佼者。ECMWF第一个在业务中实践四维变分同化（4DVAR）技术，其早在1987年制定的4年发展计划时开始酝酿用4DVAR来取代最优插值方法，此后历经十年努力，1997年11月实现了业务化运行[42]。自那时起ECMWF一直使用增量（Incremental）4DVar作为其同化系统核心算法[56]。

为了更加充分地利用当前的全球观测系统（GOS）产生连续的观测流，减少“等待观测数据到达”的时间，2019年ECMWF在同化系统中引入连续数据同化技术（Continuous Data Assimilation）[56]。连续数据同化的优势是不必等待所有观测结果到达后才开始计算，计算阶段与数据收集阶段重叠（图3）。在运行中，不再要求在固定的截止时间后停止观测进入，而是在连续的外循环之间允许新的观测进入同化系统。由于每个外循环大约需要15 min才能完成，因此在连续数据同化中，有效截止时间延长了约25 min。在此框架下可以利用比当前系统晚大约1.5 h的观测，以及在截止时间之后到达的观测。实验证实，连续数据同化能够更加充分利用观测数据并产生更准确的分析结果，系统的可预测性提高了2～3 h[56]。

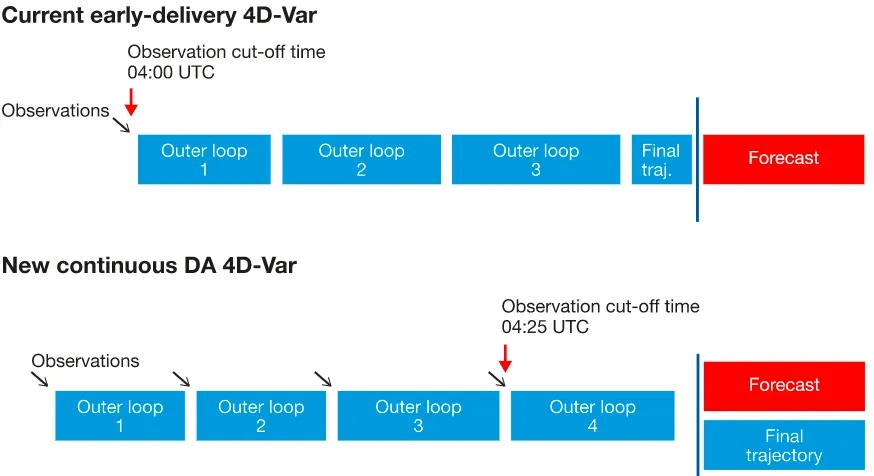
图3 早期的四维同化和当前四维连续数据同化示意（黑色箭头表示4D-Var在各阶段计算时获取的观测。蓝色竖线表示预报开始的时间并没有受到影响）[56] Fig. 3 Schematic representation of the current early-delivery 4D-Var configuration and the proposed continuous DA 4D-Var configuration. (The black arrows indicate at which stage of the 4D-Var computations new observations are ingested. The blue vertical line denotes the time when the forecast computations start, which is unchanged) [56]

此外，为改善海洋—大气之间不同系统同化时的初始化冲击，ECMWF还在积极推进耦合同化技术研发与应用。耦合数据同化能够使不同时间尺度和同化方法的地球系统各组成部分取得最大的一致性。ECMWF在2018年6月（IFS Cycle 45r1）和2019 年6月（IFS Cycle 46r1）的两次系统升级中引入了大气、海洋和海冰的弱耦合数据同化。实验证实，弱耦合海洋−大气数据同化对热带和极地地区温度和湿度等大气变量有显著的改善[57]（图4）。

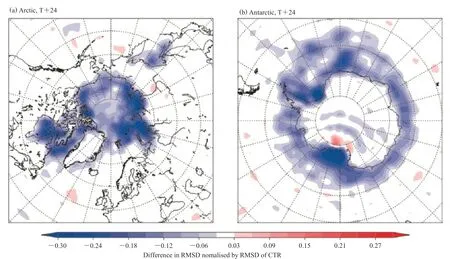
图4 北极（a）和南极（b）2017年6月9日—2018年5月21日耦合同化试验（蓝色阴影表示使用弱耦合数据同化时预测与分析之间的差异较小）[57] Fig. 4 The coupled data assimilation tests in the Arctic (a) and the Antarctic (b), for the period 9 June 2017 to 21 May 2018 . (Blue shades mean that the differences between forecasts and the analysis are smaller when weakly coupled data assimilation is used) [57]

3 讨论及总结

自20世纪90年代以来世界主要气象强国开始投入了比以往更多的人力、财力、物力致力于加速发展数值预报业务体系，并取得显著成效[17]。然而随着集合预报、数据同化理论和方法的日臻成熟，在现有科学范式下难以或者需要花费更多的代价才能取得新的重要突破。初值难以精确，模式很难完美，可预报性问题短期内尚不能显著改善，数值天气预报仍然面临诸多难题[4,58-59]。除了科学认识尚有不足，随着模式分辨率的提升、集合预报成员的增加，随之所需的计算资源和电力消耗呈指数级增长[4]，这些技术、经济上的挑战也是业务数值预报系统发展不可忽视的因素。

由于传统方法短期内难以取得显著进展，世界气象强国更加重视新兴技术在数值预报领域的研究和业务布局[37,60]。随着新一代信息技术和智能算法技术的不断进步，人工智能推动科技、产业发展和社会变革的巨大潜力得到全球更加广泛的认同。鉴于大气科学显著的非线性特征和当前气象领域典型的大数据特征①海量观测和数值模式数据，具备典型的大数据特征，即规模性（Volume）、多样性（Varity）、高速性（Velocity）和价值性（Value）。，因此利用机器学习、深度学习等人工智能的方法，借助海量的观测、模式数据来提升预报预测能力受到了的前所未有的关注并取得了积极进展[61-70]。全球主要气象机构也敏锐地捕捉到了这一发展战略机遇，并逐渐将其视为气象科技进步的重要竞争领域之一。比如，ECMWF、美国国家海洋与大气管理局（NOAA）等竞相在其最新的发展战略中除了持续推进地球系统数值模式、资料同化等传统优势领域的布局外还进一步强化了人工智能等新技术在气象领域的科学研究与业务实践[71-72]。

大气科学的每一次飞跃都伴随着与其他科学技术进步的融合发展。集合、同化思想在大气科学中的渗透、应用和发展极大地推动了以数值预报技术为核心的现代气象业务发展。当前人工智能等新一代信息技术在气象及地球系统领域的融合应用也许能够较快带来新的技术突破并为大气科学的发展注入更多的创新源泉。