深空干涉测量对流层经典模型改进
柴恬怡,路伟涛,马 宏,焦义文,张爱迪,张 宇
(1 航天工程大学电子与光学系 北京 101416;2 北京航天飞行控制中心航天飞行动力学技术重点实验室 北京 100094)
引言
甚长基线干涉测量是近年航天射电领域的热点研究技术之一,它具有测量精度高、作用距离远等优点,在深空探测中应用前景广泛[1]。干涉测量误差可分为系统误差和无线信道误差:系统误差主要包括系统噪声误差、时钟同步误差、设备相位抖动误差和站址误差;无线信道误差主要包括对流层和电离层误差、太阳等离子体误差[2]。其中,对流层误差是影响干涉测量精度的重要因素之一。
对流层是非色散介质,范围从地面至地面以上约60 km 处。对流层延迟是指电磁波信号经过大气层时受到非色散介质的影响,从而发生信号在方向和速度上改变所产生的延迟[3]。对流层延迟分为干燥气体引起的干延迟和水汽引起的湿延迟,其中干延迟约占总延迟的90%,湿延迟约占总延迟的10%[4]。
当前,修正对流层延迟主要有外部修正法、参数估计法和模型改正法。外部修正法成本昂贵,在空间和时间上的分辨率较低,参数估计法处理步骤繁琐,因此,模型改正法成为对流层延迟误差修正研究的主要部分[5]。
模型改正法通过对流层天顶延迟 (Zenith Tropospheric Delay,ZTD)与映射函数 (Mapping Functions,MF)进行对流层延迟模型构建。对流层天顶延迟模型主要包括:Hopfield模型、Saastamoinen 模 型、UNB3 模 型 和GPT2w 模 型[6]。Hopfield模型将大气温度下降率假设为常数,计算干延迟的精度为2 cm,计算湿延迟的精度为5 cm[7]。Saastamoinen 模型利用大气折射廓线及干、温对流层和干平流层各层的边界值所建立映射函数是将天顶对流层延迟模型投影到任意仰角方向上,因此,选择一个高精度的映射函数对于提高对流层延迟精度至关重要。常用的映射函数主要包括Neil 映射函数、维也纳映射函数(Vienna Mapping Functions 1,VMF1) 和全球映射函数(Global Mapping Function,GMF)[8]。Neill 利用了北美地区探空气象站的资料建立了一个全球映射函数模型,模型输入年积日和测站坐标,考虑南北半球和季节的非对称性。Neill 模型被广泛于深空干涉测量领域[7]。文献[8]利用不同纬度USB 设备的实测数据分析了NMF 模型和GMF 模型,实验结果表明:NMF 映射函数精度较高。文献[9]表明:映射函数精度主要受大气模型的偏离和映射函数连分式系数展开形式选取的影响。文献[10]确定干映射参数a为响应NMF 模型精度的主要影响参数,对参数a进行最小二乘处理可提高模型精度。
上述对流层延迟天顶模型和映射函数估计精度较高,但主要采用国外测站数据构建,在我国测站区域的适用性还需进一步分析[11]。NMF 模型在仰角大于30°时,修正偏差均小于15 cm,仰角小于30°时,修正偏差较大[8]。基于此,本文结合我国深空网喀什深空站实测对流层延迟数据、大气参数数据(大气温度、湿度、压强)对Saastamoinen 模型和Neill 映射函数进行分析,构建对流层延迟改进模型,并进行实验验证。
1 对流层经典模型性能分析
对流层延迟(dDELAY)是将电波传播斜路径上的折射误差看成对流层天顶延迟(dZTD)与映射函数(fMF)的乘积[7]:
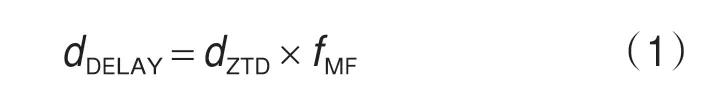
dZTD是仰角等于90°时的对流层延迟,然后通过fMF可以得到其他观测仰角条件下的对流层延迟。如果对流层天顶延迟模型存在误差,则该误差将通过fMF传递到所有仰角的模型值,即天顶延迟模型是全仰角影响因素。Saastamoinen模型如式(2)所示:
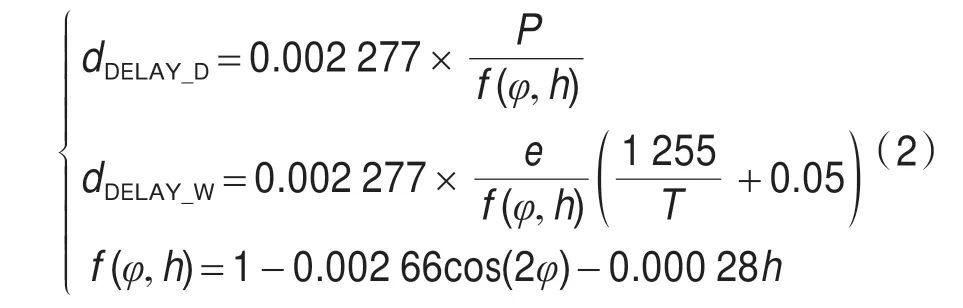
其中,dDELAY_D为对流层延迟干延迟,dDELAY_W为对流层延迟湿延迟,φ表示测站纬度(单位:rad),P、T和e表示地表处的气压(单位:m),温度(单位:K)和水汽压(单位:Mbar),h为测站高程(单位:m)。由于Saastamoinen模型采用分层积分来描述中性大气,且湿延迟模型中温度梯度计算精确[8],因此被广泛应用在深空干涉测量对流层误差修正中。
NMF 模型包括干映射函数和湿映射函数,干映射函数如式(3)所示[10]:

湿映射函数如式(4)所示:
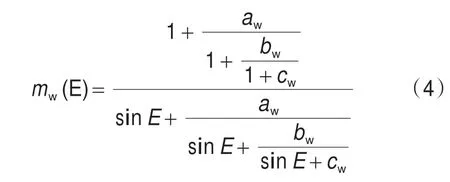
其中,E为高度角(单位:rad),h为测站高程(单 位:km),aht=2.53×10-5,bht=5.49×10-3,cht=1.14×10-3。ad、bd和cd均为干分量系数。
通过喀什深空站2018年12月30日对流层延迟模型值与实测值进行差值运算,得到实验结果如下(图1为对流层延迟模型值与实测值差值图)。
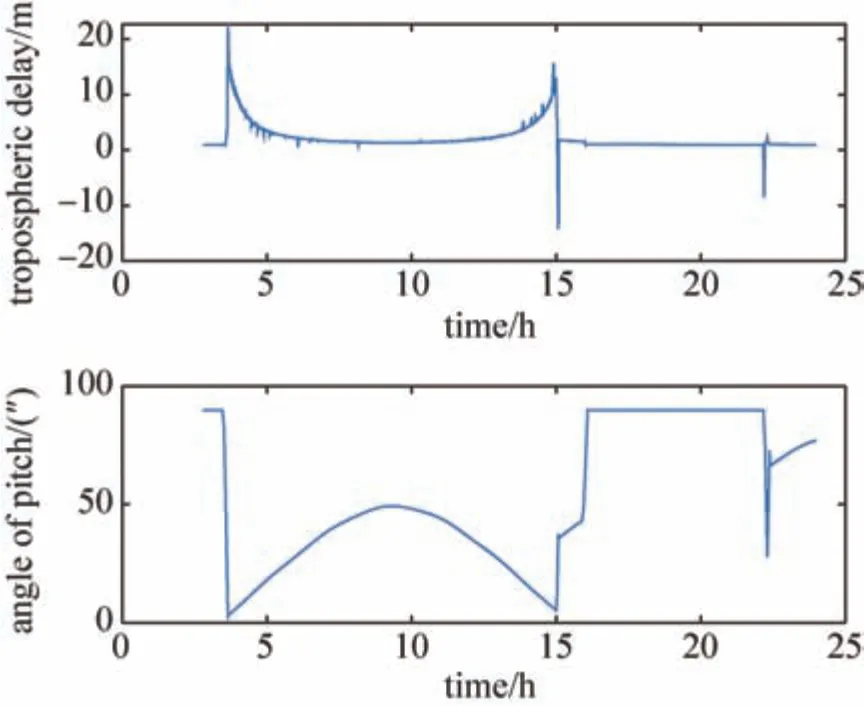
图1 对流层延迟模型值与实测值差值(2018年12月30日)Fig.1 Difference between tropospheric delay model value and measured value (30 December 2018)
由图1可以看出:不同仰角下对流层延迟偏差不一致,表明Niell 模型存在偏差。Niell 模型未利用我国地区的观测数据而建立,因此,Niell 模型在我国深空站低仰角区域的映射性能还需进一步改善。
2 区域天顶模型参数修正
Saastamoinen 模型是一种典型的高精度天顶模型,应用广泛[12]。但是对流层天顶模型精度影响所有仰角下的对流层延迟修正效果,因此有必要分析Saastamoinen模型在我国深空站区域的适用性。
习近平总书记指出:“大数据是工业社会的‘自由’资源,谁掌握了数据,谁就掌握了主动权。”大数据正在成为经济社会发展新的驱动力。在产品质量领域,大数据可以为企业设计产品、防范风险提供依据,为政府加强监管提供技术支撑,为维护国家市场权益提供保障。如何客观分析产品质量大数据建设、利用状况及存在的问题,是充分发挥大数据在产品质量治理中的作用必须面对的现实问题。
通过对喀什深空站2018 年12 月5 日—2019 年1 月15 日中33 天的天顶实测数据进行分析,将实测气象数据代入Saastamoinen 模型中解算出模型值,与实测延迟值对比仿真,得到实验结果如下(图2为ZTD模型和实测对比仿真图)。
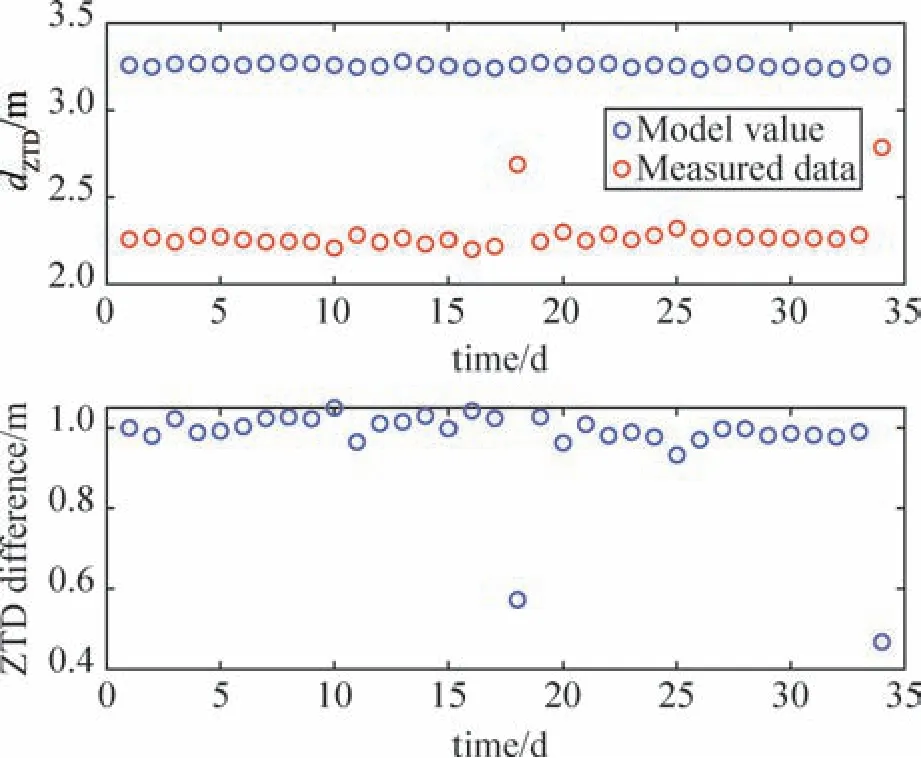
图2 对流层天顶模型值与实测值对比Fig.2 Comparison between tropospheric zenith model values and measured values
由图2可以看出,对流层天顶延迟模型值明显大于实测值。模型值相对稳定,实测值个别点波动明显。模型值平均结果为3.258 1 m,实测值平均结果为2.288 m,模型值与实测值偏差均值为0.970 1 m,存在明显偏差。通过分析Saastamoinen模型规律,确定干映射参数a为响应的主要影响参数[13]。Saastamoinen模型干延迟公式如下。
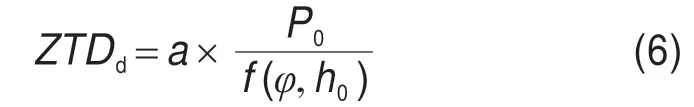
以实测所得天顶延迟值为观测值,建立误差方程。

其中,y为实测天顶干延迟值。通过对喀什深空站2018 年12 月5 日—2019 年1 月5 日 中26 天 的 天 顶数据进行仿真实验,线性最小二乘拟合出a为0.001 6。为了说明改进模型的有效性,利用喀什深空站2019 年1 月6 日—2019 年1 月15 日中7 天数据进行验证,结果如表1所示。
由表1 可知:喀什深空站2019 年1 月中7 天修正前模型偏差约为0.986 5 m,修正后模型偏差约为0.026 m,修正精度提高一个量级,修正效果明显。通过对喀什深空站2019年1月8日数据进行仿真,实验结果如图3所示。
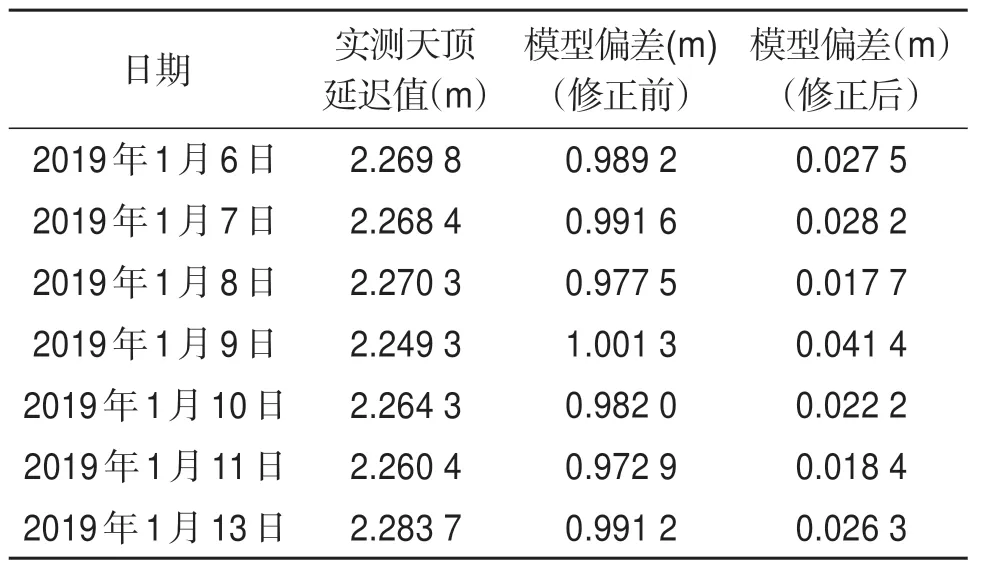
表1 喀什深空站2019年1月中7天对流层天顶延迟值Table 1 7days tropospheric zenith delay of Kashi Deep Space Station in January 2019
修正前模型值平均结果为3.247 m,实测值平均结果为2.270 3 m。系数a修正后,模型值平均结果为2.287 9 m。模型差值图如图3所示。
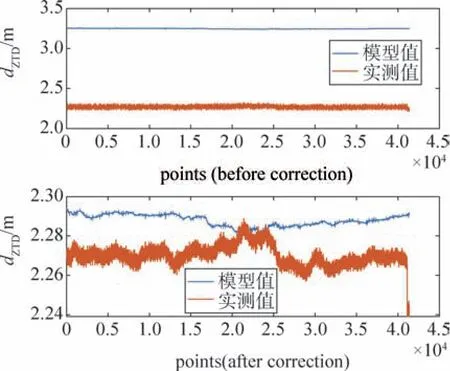
图3 对流层天顶模型值与实测值对比(2019年1月8日数据)Fig.3 Comparison of tropospheric zenith model values with measured values (data of January 8,2019)
由图4可以看出,修正前模型偏差平均结果为0.977 5 m,系数a修正后,对流层天顶延迟偏差均值为0.017 7 m,提高了一个量级。
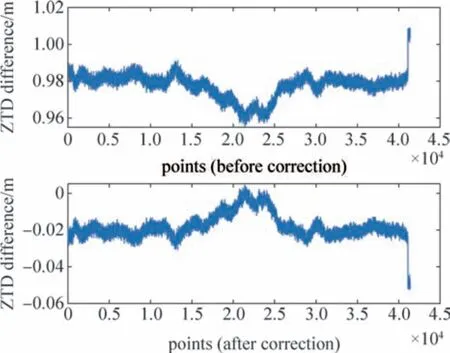
图4 模型值和实测值差分值(2019年1月8日41 385个数据)Fig.4 Difference between model value and measured value (data of January 8,2019)
3 区域Neill模型参数修正
工程实践表明:对流层延迟模型误差随仰角降低而显著增加[14]。因此,映射函数在低仰角条件下的准确性还需进一步研究。通过分析Niell 映射函数规律,针对低仰角情况下模型值相较于实测值存在较大偏差,构建误差模型,如式(8)所示。使用喀什测深空站2018 年12 月5 日—2019 年1 月5 日中26 天低仰角(0°~30°)对流层延迟实测数据进行仿真实验。
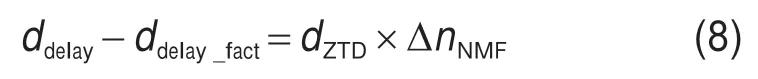
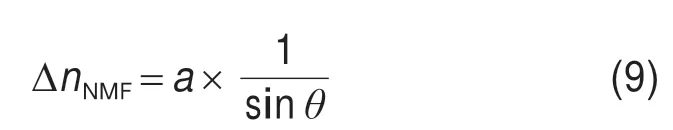
线性最小二乘拟合得到a的值为0.287。再用喀什深空站2019 年1 月6 日—2019 年1 月15 日中7天低仰角数据进行验证,结果如表2所示。

表2 喀什深空站2019年1月中7天15°俯仰角下对流层延迟值Table 2 Tropospheric delay at 15° elevation for 7 days at Kashi Deep Space Station in January 2019
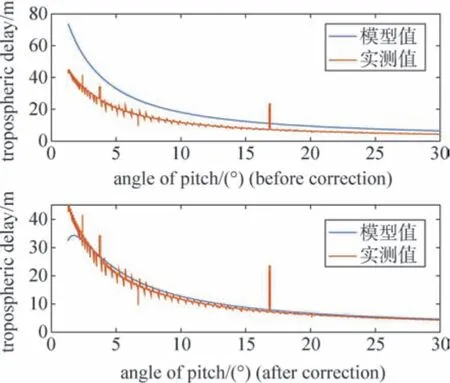
图5 低仰角对流层延迟修正(2019年1月13日数据)Fig.5 Low elevation tropospheric delay correction (data of 13 January 2019)
由图5 可以看出:在喀什深空站由Niell 映射函数得到的对流层延迟值与实测偏差明显,模型对流层延迟均值为17.992 1 m,实测延迟值均值为11.522 6 m,且仰角越低,偏差越大。在修正后,两者偏差缩小,模型均值为12.295 3 m。修正前后偏差如图5所示。
由图6可以看出:修正前模型值与实测偏差明显,在仰角5°时,与实测数据偏差为12.67 m,修正幅度为38.2%;在仰角10°时,与实测数据偏差为6.438 m,修正幅度为35.4%;在仰角30°时,与实测数据偏差为2.164 m,修正幅度为33.2%。修正后模型值与实测偏差较小,且偏差值稳定。在仰角5°时,改进模型相对经验模型偏差为10.74 m,与实测数据偏差为1.92 m,修正改善幅度为32.4%;在仰角10°时,改进模型相对经验模型偏差为5.414 m,与实测数据偏差为1.272 m,修正改善幅度为29.7%;在仰角30°时,改进模型相对经验模型偏差为1.879 m,与实测数据偏差仅为0.284 1 m,修正改善幅度为28.8%。
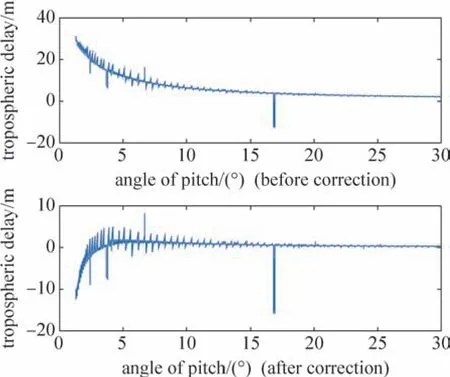
图6 低仰角对流层延迟修正差值分布(2019年1月13日数据)Fig.6 Low elevation tropospheric delay corrected difference distribution (data of January 13,2019)
4 结束语
本文首先对Saastamoinen 模型进行适用性分析,利用喀什深空站2018 年12 月5 日—2019 年1月5 日中26 天对流层延迟实测数据,通过线性最小二乘拟合天顶干延迟中的参数a为0.001 6,利用喀什深空站2019 年1 月6 日—2019 年1 月15 日中7天数据进行验证,修正前模型偏差约为0.986 5 m,修正后模型偏差约为0.026 m,对流层天顶模型精度提高了一个量级。
然后,通过分析Niell 映射函数规律,针对低仰角情况下延迟值相较于实测值存在较大偏差,构建偏差函数,利用喀什深空站2018 年12 月5 日—2019年1月5日中26天低仰角(0°~30°)数据进行验证,在仰角15°时,喀什深空站2019 年1 月6 日—2019 年1 月15 日中7 天修正前模型值约为18.14 m,实测对流层延迟约为11.72 m,修正后模型值约为12.74 m,修正改善幅度为30%。目前,适用于中国深空站对流层模型研究报道较少,因此,改进现有的经典模型来进一步提高对流层延迟修正精度,能够适应深空探测、射电天文和大地测量等多种任务的观测需求,对于我国深空探测干涉测量任务具有较好的工程应用价值,对我国深空站大气介质时延模型实时估计相关技术的研究将具有重要的理论研究意义和实用价值。
——环地平弧&环天顶弧

