建筑群布局对燃煤电厂周边CO2分布特征的影响研究

陈浈斐，陈金玺，范晨阳，晏 璐

(河海大学能源与电气学院，江苏省南京市，211100)

0 引言

我国“富煤、贫油、少气”的能源特点，决定了煤炭在我国一次能源的生产和消费中，短期内难以发生根本性改变[1]。根据中电联报告显示，全国发电总装机容量为24亿kW，其中煤炭发电装机容量为11.1亿kW，占比为46.3%，同比增加2.5%。在未来一段时间内，我国的煤炭发电仍将占据主要地位[2-5]。因此，目前我国仍在规划和建设一定数量的燃煤电厂，以保证电力需求得到充足供应[6-7]。

由于燃煤电厂以燃煤为主，煤燃烧会对周边环境会产生一定影响。随着近年来碳中和目标的提出，燃煤电厂的碳排放研究成为重点。盖志杰等研究人员[8]以2台300 MW的燃煤发电机组为研究对象，计算该电厂3年的碳排放总量；高建强等研究人员[9]以330 MW燃煤机组为研究对象，探究在58%、74%、89%负荷下，碳排放强度在各系统中的折算比例以及随负荷变换的规律；蔡宇等研究人员[10]以内蒙古自治区某燃煤电厂为研究对象，介绍了碳排放量的计算过程以及碳排放量与供电量之间的定量关系；孙友源等研究人员[11]提出了2种碳排放强度的计算模型并给出计算实例；王通、索新良等研究人员[12-13]以燃煤发电机组为例，阐述燃煤电厂CO2排放量的测算方法，对计算CO2排放量意义重大。上述文献是研究燃煤电厂发电量与碳排放量之间的折算比，并据此估算出实际的碳排放量。

随着“低碳城市”的理念从提出到推广，针对城市碳排放的研究也取得丰富成果。马明义等研究人员[14]从多维视角下研究了新型城市化对我国二氧化碳排放影响的时空变化特征；王雅楠等研究人员[15]利用面板门槛模型研究城镇化对碳排放的影响及其区域空间分布；王睿等研究人员[16]以县级市作为研究单位，探究了我国县级市碳排放空间分布格局及人口、经济对碳排放的影响；夏冰等研究人员[17]以城市街区为研究对象，从城市街区碳排放计算与评估、碳排放与街区形态关联性等相关方面，对目前已有低碳城市街区形态导控方法进行了整理与分析。上述文献分别从宏观和微观角度对城市碳排放时空分布特征进行研究。

研究表明，CO2本身并没有毒性，但如果长时间处于CO2浓度超过10%的环境中，人体的呼吸系统、循环系统、大脑器官的机能就会受到影响，并引起头痛、酸中毒和心悸等症状[18-19]。因此，笔者为研究城市中燃煤电厂排放CO2对其周边居民的影响，采用计算流体动力学(CFD)模拟技术，对燃煤电厂及周边建筑群进行有限元建模，研究不同风速和烟囱高度影响下燃煤电厂周边CO2含量的分布情况，并通过改变燃煤电厂周边建筑群的布局结构，研究出建筑群布局对CO2含量及速度场分布的影响，并剖析CO2的扩散规律，为燃煤电厂周围区域规划以及建筑群布局提供理论依据。

1 仿真模型建立

1.1 物理模型

为了研究城市中燃煤电厂排放的CO2浓度对其周边居民的影响，笔者采用CFD模拟技术搭建了燃煤电厂及其周边建筑群的仿真模型，并结合流体力学方程设置仿真边界条件，以空气中的CO2含量为研究对象进行分析。CFD分析法不仅模拟周期短、收敛速度快、经济性好且可以通过改变参数，迅速实现流体的运动状态，得出计算结果。燃煤电厂及下风向水平型建筑群布局如图1所示。

图1 燃煤电厂及下风向水平型建筑群布局

仿真模型中，设置燃煤电厂烟囱为CO2排放源头，其碳排放量为1 000 kg/s。设置烟囱直径为10 m，位于居民建筑群左侧，烟囱周围有6栋边长为10 m的正方形燃煤电厂建筑。居民建筑群一共设置了16栋居民楼，每栋居民楼的长度25 m、宽度10 m、相邻居民楼之间的距离为10 m。整个仿真计算域大小为530 m×310 m×140 m(X,Y,Z)，如图1所示。图中L1、L2、L3、L4、L5、L6、D-1、D-2、D-3、D-4是分析CO2含量分布所设置的采样线，CO2质量分数采样线的位置坐标参数见表1。

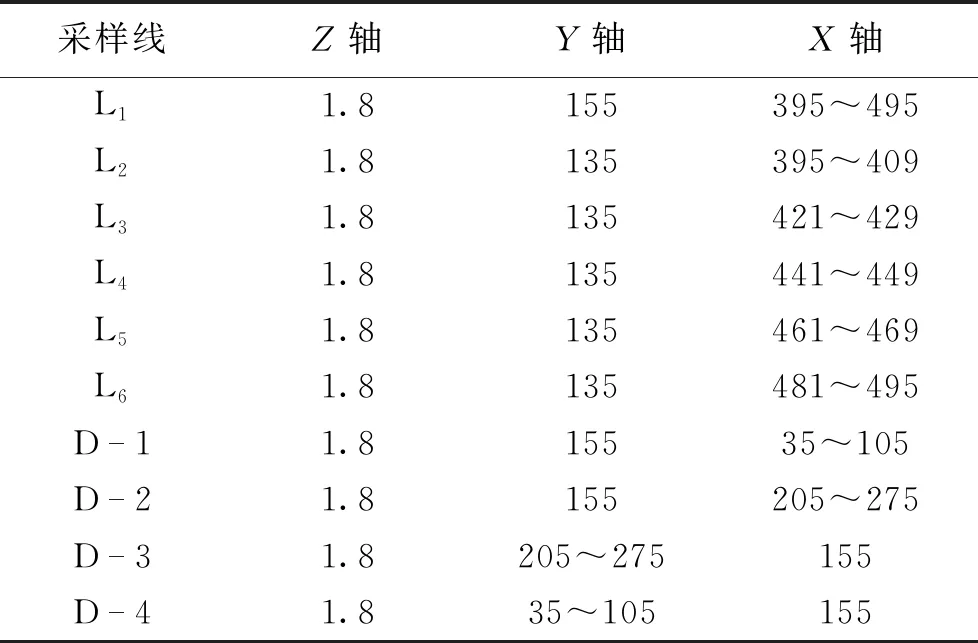
表1 CO2质量分数采样线的位置坐标参数 m

1.2 流体动力学方程

流体流动受物理守恒定律的支配，从本质讲基本守恒定律由能量守恒定律、质量守恒定律和牛顿第二定律组成。对于空气动力学而言，流体力学基本方程组是由连续性方程、动量守恒方程、能量守恒方程组成。

连续性方程见式(1)：

(1)

式中：∂——对各变量求偏导；

ρ——质量密度， kg/m3；

t——时间， s；

u、v、w——流速在各个方向上的分量， m/s；

x、y、z——速度方向。

动量守恒方程见式(2)：

(2)

式中：p——气流压力， Pa；

v——粘性系数， Pa·s；

Su——动量源项， kg·m/s；

ui、uj——流体在对应方向上的平均速度，m/s；

xi、xj——笛卡尔坐标分量，i、j的范围在1～3之间。

能量守恒方程见式(3)：

(3)

式中：θ——位温， K；

Km——热量扩散系数， m/s；

Sθ——能量源项， J。

当研究气体扩散时，应根据气体的特性添加组分输运方程。考虑到居民主要在地面活动，笔者采用k-ε输送方程，k-ε输送方程见式(4)和式(5)：

式中：k——湍流动能， J；

vt——湍流粘性系数， m2/s；

u——湍流流动的流速， m/s；

ε——湍流耗散率， %；

Cμ，Cε1，Cε2，σk，σε——k-ε输送方程常数，分别取值为0.09、1.44、1.92、1.30、1.00。

组分输运方程见式(6)：

(6)

式中：Ci——i点处气体浓度，mg/m3；

K——湍流扩散系数， m/s；

S——气体源项， mg/(m·s)。

1.3 CO2质量分数定义

常见的气体含量表示方法有6种，分别是摩尔分数x、质量摩尔浓度m、质量分数w、质量浓度p、体积分数φ、物质的量浓度c。笔者采用CO2质量分数来代表气体的含量见式(7)：

(7)

式中：wB——组分气体的质量分数；

mB——组分气体的质量， g/L；

mm——混合气体中各组分的质量之和， g/L。

2 风速对CO2含量影响分析

风速是影响燃煤电厂排放气体扩散的重要因素之一，在研究CO2含量分布时，在无风和有风这2种情况下，对燃煤电厂周边4个方向上的CO2质量分数进行了仿真分析。

假设燃煤电厂烟囱高度设置为100 m，建筑群类型为水平型，无风和有风时CO2质量分数变化曲线如图2所示。

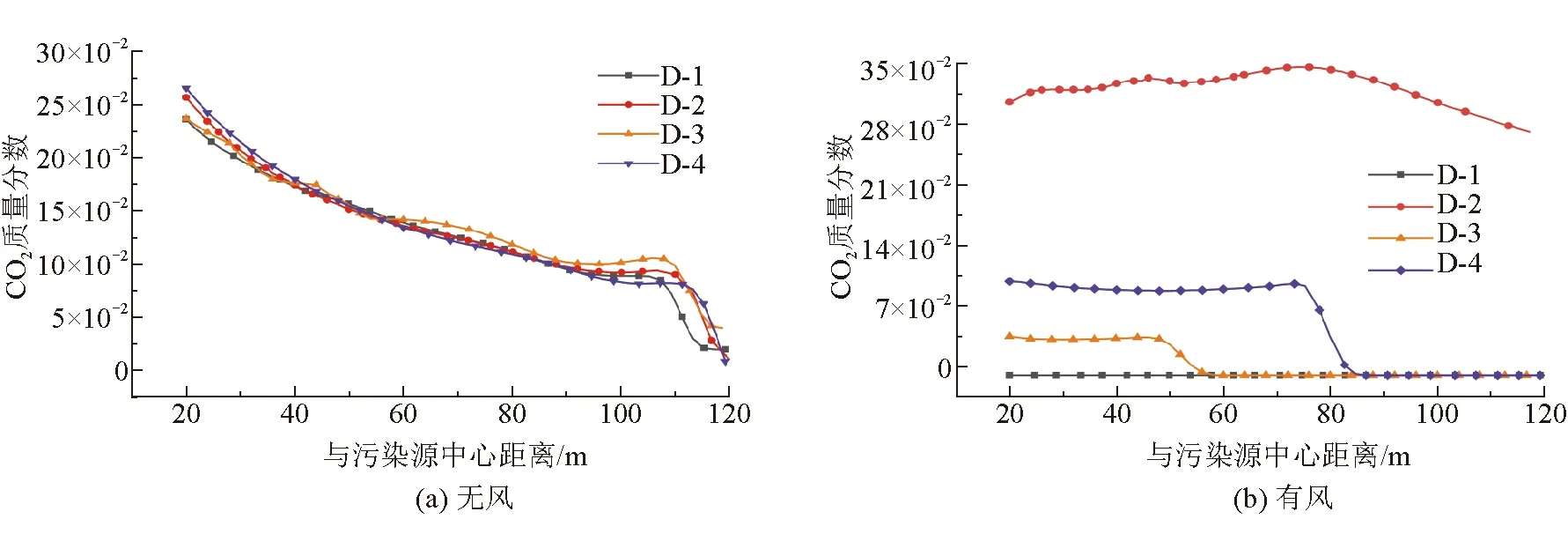
图2 CO2质量分数变化曲线

由图2(a)可以看出，无风时碳排放源周边4个方向的CO2质量分数相差不大，且变化规律基本相同，离排放源越远CO2浓度越低；由图2(b)可以看出，有风时下风向附近CO2的质量分数与其他方向的CO2质量分数相比，其数值呈现指数级上升，说明在有风的情况下，CO2主要朝下风向扩散。

因此，笔者重点研究分析了燃煤电厂下风向CO2含量的分布。

为进一步研究不同风速对燃煤电厂周围CO2含量的影响，设置了5 m/s和7 m/s2种风速，对图1中提到的L1～L66条采样线处的CO2质量分数进行仿真，不同风速下CO2质量分数变化曲线如图3所示。

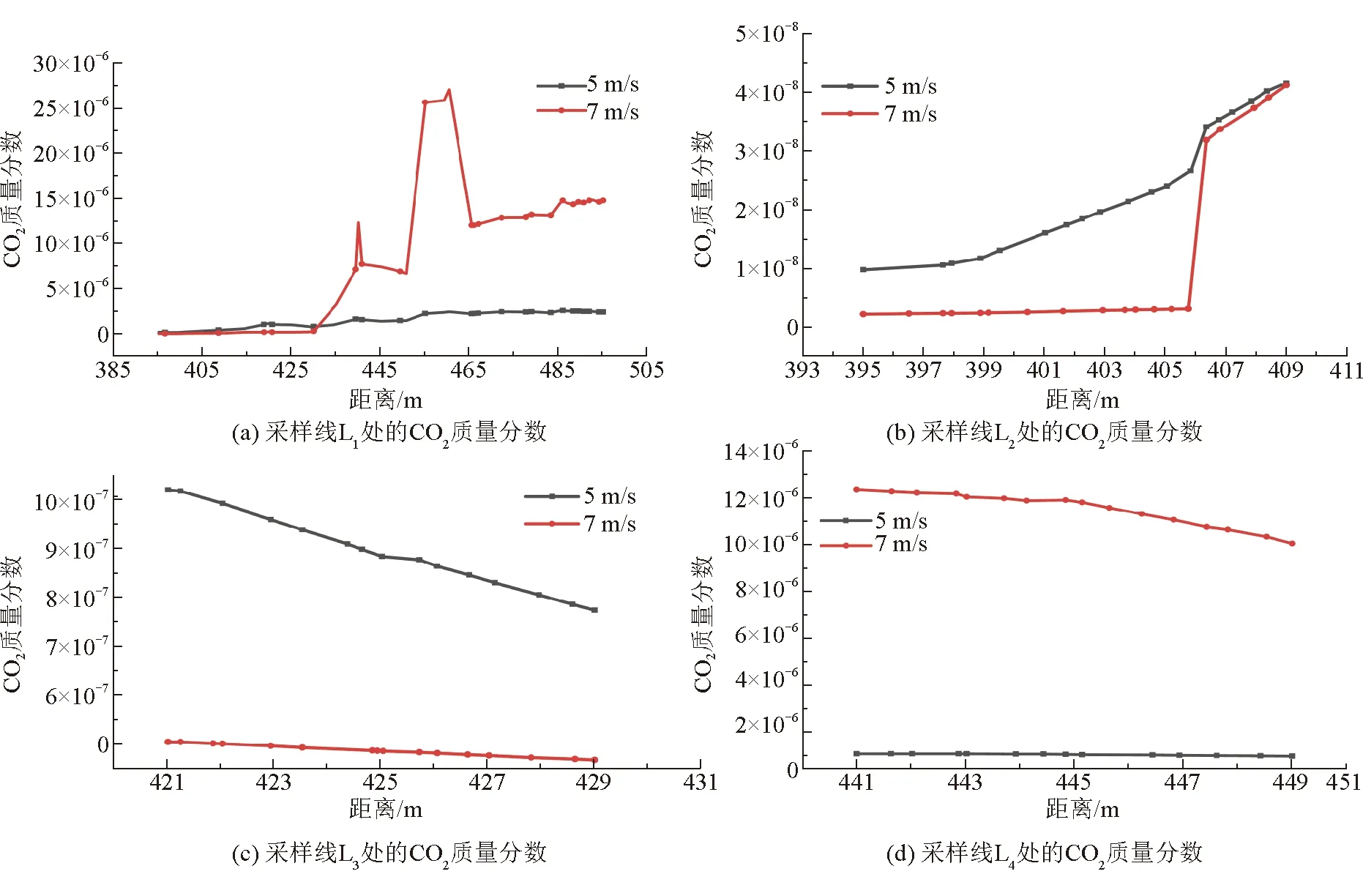
图3 不同风速下CO2质量分数变化曲线

由图3 (a) 可以看出，当风速为5 m/s时，CO2质量分数呈现上升趋势，当风速为7 m/s时，CO2质量分数总体上呈现振荡上升的趋势。在距离395～430 m时，风速为5 m/s的CO2质量分数要比风速为7 m/s的高；在距离430～495 m时，风速为7 m/s的CO2质量分数要比风速为5 m/s的高。

由图3 (b)和图3(c) 可以看出，在距离395～409 m及421～429 m时，风速为5 m/s的CO2质量分数要比风速为7 m/s的高。

由图3 (d)～图(f) 可以看出，在距离441～449 m、461～469 m及481～495 m时，风速为7 m/s的CO2质量分数要比风速为5 m/s的高，且当距离超过488 m时，两者的CO2质量分数都接近于零。

由图3整体可以看出，风速的大小会对燃煤电厂下风向周边建筑群CO2的含量产生影响。风速越大，大气湍流就越强，CO2就扩散的更快。因此，当风速变大时，与碳排放源相距较远处的CO2含量会增加，与碳排放源相距较近处的CO2含量会降低。所以，在确定建筑群与燃煤电厂的距离时，应结合当地的月平均风速进行综合考虑，以保证居民生活的舒适度。

3 排放源高度对CO2含量影响分析

通过将燃煤电厂的烟囱高度分别设置成100 m和120 m，进一步研究排放源高度对CO2扩散的影响。此时，将风速设置为7 m/s，不同碳排放源高度下CO2质量分数变化曲线如图4所示。

图4 不同碳排放源高度下CO2质量分数变化曲线

由图4 (a) 可以看出，在燃煤电厂距离建筑物395～495 m时，碳排放源高度为120 m的CO2质量分数与碳排放源高度为100 m的CO2质量分数相比呈指数级下降，且当距离小于285 m时，两者的CO2质量分数都接近于零。

由图4(b)～(f)可以看出，在燃煤电厂距离建筑物395～409 m、421～429 m、441～449 m、461～469 m及481～495 m时，碳排放源高度为120 m的CO2质量分数与碳排放源高度为100 m的CO2质量分数相比呈指数级下降，且当距离超过343 m时，两者的CO2质量分数都接近于零。

由图4整体可以看出，当燃煤电厂烟囱高度从100 m 升至120 m时，燃煤电厂下风向相同位置的CO2质量分数呈指数级下降。因此，可以适当增加燃煤电厂烟囱高度以降低燃煤电厂下风向建筑群周边区域CO2质量分数。

4 建筑群类型对CO2含量影响分析

为了进一步分析燃煤电厂周边建筑群结构类型对CO2含量的影响，建立了水平型、下降型、凹字型、上升型、凸字型这5种典型建筑群的仿真模型，对建筑群中的空气流速和CO2含量进行仿真分析。燃煤电厂的烟囱高度设置为100 m，并将风速设置为7 m/s。水平型建筑群的具体结构和参数如图1所示；其他4种类型的建筑群中建筑物的长度、宽度与水平型相同，不同类型的建筑群高度及结构如图5所示。

图5 不同类型的建筑群高度及结构

4.1 不同类型建筑群对气流的影响

燃煤电厂排放的CO2主要从烟囱集中排放，其周边CO2含量的分布会受到气体流速的影响。而不同建筑群类型对气流的影响也不同，间接影响到空气中CO2的含量分布。因此，研究了不同建筑群类型对CO2气体流速的影响。不同类型建筑群中CO2气体流速分布如图6所示。

由图6(a)可以看出，在水平型建筑群中，气流在建筑物A和D之间仅形成了较小的逆时针漩涡，在C和D之间的漩涡稍强，并在建筑物D后方沿着墙面逆时针进行爬升；由图6(b)可以看出，在凸字型建筑群中，气流在建筑物D的上方形成一个较大的逆时针漩涡，且在建筑物B后方有上升趋势，由于建筑物B的遮挡，气流速度在建筑物A和B之间得到提升；由图6(c)可以看出，在凹字型建筑群中，气流在建筑物B和D的上方形成一个较大的逆时针漩涡，且在建筑物A后方有先升后降的趋势，建筑物D后方沿着墙面逆时针进行爬升；由图6(d)可以看出，在上升型建筑群中，建筑物之间没有形成逆时针漩涡，但相邻建筑物之间的气流速度得到提升，且在建筑物D后方沿着墙面逆时针进行爬升；由图6(e)可以看出，在下降型建筑群中，气流在建筑物B和C上方形成一个较大的逆时针漩涡，且在建筑物D后方形成了一个小型漩涡，此外，气流在经过建筑物A后呈现下降趋势。

图6 不同类型建筑群中CO2气体流速分布

4.2 不同类型建筑群中的CO2含量分布

在分析不同类型建筑群中气体流速的基础上，进一步对建筑群中的CO2含量进行分析。不同类型建筑群中6条采样线处CO2质量分数分布情况如图7所示。

由图7(a)可以看出，在燃煤电厂距离建筑物385～485 m时，凹字型建筑群的CO2质量分数呈现增大趋势，上升型建筑群的CO2质量分数总体呈现震荡趋势，其余类型建筑群的CO2质量分数近似保持不变且接近于零；由图7(b)可以看出，在燃煤电厂距离建筑物385～409 m时，凹字型和水平型建筑群的CO2质量分数呈现上升趋势，其他类型建筑群的CO2质量分数近似不变且接近于零；由图7(c)可以看出，在燃煤电厂距离建筑物421～429 m时，凹字型、上升型、凸字型建筑群的CO2质量分数呈现出下降趋势，其他类型建筑群的CO2质量分数总体上保持不变且接近于零；由图7(d)可知，在燃煤电厂距离建筑物441～449 m时，上升型建筑群的CO2质量分数呈现上升趋势，其他类型建筑群的CO2质量分数总体上保持不变且接近于零；由图7(e)可以看出，在燃煤电厂距离建筑物461～469 m时，上升型和凹字型建筑群的CO2质量分数呈现上升趋势，其他类型建筑群的CO2质量分数总体上保持不变且接近于零；由图7(f)可以看出，在燃煤电厂距离建筑物481～495 m时，上升型和凹字型建筑群的CO2质量分数呈现出先上升后下降的趋势，其他类型建筑群的CO2质量分数总体上保持不变且接近于零。

由图7整体可以看出，凸字型和下降型建筑群附近的CO2质量分数较低，适合作为燃煤电厂下风向建筑群。

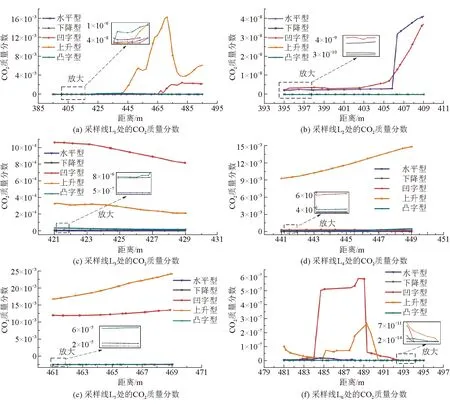
图7 不同类型建筑群CO2质量分数分布

5 结论

随着城市低碳环保工作的推进，居民对其居住环境中的CO2浓度的关注度也逐渐提高。笔者采用CFD模拟技术对燃煤电厂及周边建筑群进行有限元建模，研究了风速、排放源高度和建筑群类型等因素影响下燃煤电厂周边CO2含量分布情况。得出以下结论。

(1)无风时CO2在碳排放源周边均匀扩散，4个方向的CO2含量相差不大，变化规律基本相同；有风时CO2主要朝碳排放源下风向方向扩散，下风向方向上的CO2含量与其他方向的CO2含量相比较高。

(2)风速和碳排放源的高度会对下风向建筑群附近的CO2含量产生影响。当风速增大时，与排放源相距较近处的CO2含量降低，与碳排放源相距较远处的CO2含量增加；当燃煤电厂烟囱高度增加时，地表相同高度的CO2含量会呈现大幅下降。

(3)当风速以及碳排放源高度相同时，不同类型建筑群附近的CO2含量也有所不同。在水平型、凸字型、凹字型、上升型和下降型这5种类型建筑群中，下降型和凸字型建筑群附近的CO2含量较低，适合作为燃煤电厂周边的建筑群类型。