在“正态分布”教学中渗透数学文化之美
范世祥
正态分布是概率论中重要的连续型概率模型。然而在高中阶段,受学生知识水平的限制,正态分布的许多结论无法严格证明或直接计算,在教学中教师往往一带而过。为挖掘该课题的内在教学价值,笔者深入研究教学内容,结合自身教学实践,得出了以下认识与思考。
“正态分布”是“随机变量及其分布”的最后一节,安排在随机变量、离散型随机变量及其分布列、离散型随机变量的均值与方差之后。从本节课的教学内容来看,重点是正态分布的概念及性质,难点是正态分布概念的形成与理解,尤其是正态分布密度函数解析式。从正态分布在数学中的地位以及正态分布的发展历史来看,本节内容包含了巨大的应用价值与文化价值。因此,笔者认为本节课定位于数学文化课与研究课比较适宜。教师可以引导学生通过对正态分布相关知识的学习与课后研究,了解正态分布的发展历程,认识统计学的重要性及其广泛的应用,体会数学的博大精深与数学的美,培养学生的研究能力,提升学生的科学素养。
1.对此引入方式
笔者综合了各版本教材“正态分布”这部分内容的引入方式,发现大体可以分成两种。第一种是从具体实例出发,描述误差数据的分布引入,引导学生认识误差随机变量的取值无法一一列举;第二种是借助计算机模拟,以高尔顿钉板的演示引入,在问题的引导下,学生利用所学的统计学知识进行数据处理——从频率分布直方图到频率分布折线图再到总体密度曲线引出正态分布的密度曲线,从离散型到连续型过渡,使学生历经形成对正态分布最直观最初步的认识。
无论哪种引入方式,都突出了对数据的分析与处理,其目的在于培养学生的数据分析素养。两种引入方式对数据分析从育人的价值上做了引领,并将其落实到三个方面:一是提升学生主动获取信息、定量分析的意识和能力;二是形成通过数据认识事物的思维品质;三是积累基于数据的活动经验。
2.优化内容生成
本节课的内容主要分为两个部分,第一部分是正态分布概念的形成,第二部分是正态曲线的性质探究及应用。对于第二部分,从正态分布密度函数的解析式出发,结合数学软件等工具,学生不难获得正态曲线的特点并能利用3σ原则解决相关问题。
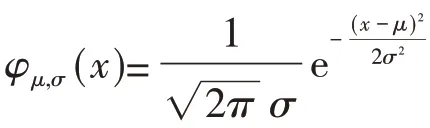
的获得,这一层面恰恰是学生感到最为困惑的。如何让学生更清晰、准确地理解正态分布的概念,笔者认为可以尝试以下三个步骤的教学。
第一,演示高尔顿钉板试验,借助数据分析作图首先可以使学生得到第一层面中对“钟形曲线”的认识;再通过分析高尔顿钉板试验结果以及其他实例引导学生得到第二个层面中对“众多的、互不相干的、不分主次的偶然因素作用结果之和”的理解,并从实例中数据的均值与离散程度明确均值μ与标准差σ是正态分布中最重要的两个参数,为第三个层面的突破做准备。
第二,结合正态曲线图象在x轴上方以及其对称性引导学生大胆猜想密度函数解析式的大致形式。
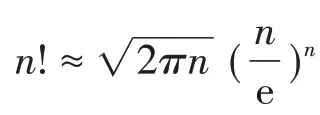
3.感悟数学之美

高中数学教师用书上建议本节课以一课时完成,在一个课时内完成这样的教学任务,使得学生既掌握正态分布的相关知识又能感受到其中所蕴含的丰富文化历史背景还是比较困难的。如何利用好这节课的文化价值?笔者认为可以布置研究性学习的任务,先让学生搜集正态分布的起源、发展、应用等相关数学素材,再分组合作写成研究报告,最后选择一些出色的小组在课堂上给全班同学做展示。
《普通高中数学课程标准(2017年版2020年修订)》指出:数学是人类文化的重要组成部分,高中数学课程应提倡数学的文化价值。笔者认为这节课的价值在高考之外,教师认真对待这节课,可以开拓学生的视野,对学生数学素养的提升有着很多益处,同时也可促进教师自身的专业发展。

