Shape Effect of Nanoparticles on Nanofluid Flow Containing Gyrotactic Microorganisms

Umair Rashid,Azhar Iqbaland Abdullah M.Alsharif

1School of Mathematical Sciences,Jiangsu University,Zhenjiang,212013,China

2Department of Mathematics and Natural Sciences,Prince Mohammad Bin Fahd University,Al Khobar,31952,Saudi Arabia

3Department of Mathematics and Statistics,College of Science,Taif University,Taif,21944,Saudi Arabia

ABSTRACT In this paper,we discussed the effect of nanoparticles shape on bioconvection nanofluid flow over the vertical cone in a permeable medium.The nanofluid contains water, Al2O3 nanoparticles with sphere (spherical) and lamina(non-spherical)shapes and motile microorganisms.The phenomena of heat absorption/generation,Joule heating and thermal radiation with chemical reactions have been incorporated.The similarity transformations technique is used to transform a governing system of partial differential equations into ordinary differential equations.The numerical bvp4c MATLAB program is used to find the solution of ordinary differential equations.The interesting aspects of pertinent parameters on mass transfer,energy,concentration,and density of the motile microorganisms’profiles are computed and discussed.Our analysis depicts that the performance of sphere shape nanoparticles in the form of velocity distribution, temperature distribution, skin friction, Sherwood number and Motile density number is better than lamina(non-spherical)shapes nanoparticles.

KEYWORDS Nanoparticle shape;nanofluid;numerical technique;gyrotactic microorganisms;magnetohydrodynamics

Nomenclature

1 Introduction

Nanofluid has become an essential topic of research because of its low thermal resistance and effective thermophysical.Furthermore,cooling is required to sustain the performance of a wide range of technologies and industrial items, including power electronics, laptops, computers, high-powered rays, and motor engines.Nanofluid technology is the most exciting development in recent years,with extremely high production and low cost.Nanofluid attribute to nanoparticles suspended in the base fluid.The very first-time idea of nanofluid was introduced by Aman et al.[1–3].Also,the nanofluid in the existence of bioconvection is become the attention of researchers because of its extensive use in biomedical, bio-microsystem, and biotechnology.In several industrial processes,including enzyme biosensors, microbial enhanced crude oil recovery, and chip size microdevices for assessing nanoparticle toxicity, the interaction between convection induces motile microorganisms,and solid particles are also important[4].Geng et al.[5]discussed the impacts of nanoparticles on the growth of bioconvection induced by plums.Uddin et al.[6]discussed the application of bioconvection and nanobiofuel with the inaction of nanoparticles.Kuznetsov[7]used the motile microorganism in nanofluid flow to increase mass transfer, microscale mixing, and the nanofluid’s expected stability.Furthermore, several studies related to the biological nanofluid and motile microorganisms are discussed[8,9].

Bio-convection is an increasing surprise of liquid mechanics determined by the swimming of microorganisms and was observed a few years ago.Bio-convection designs generally show up because of the upswimming of microorganisms with a denser density than water.The bio-convection has several applications in biotechnology and normal system.Microorganisms particles have been broadly used to make business things and mechanical such as ethanol,composts,and biofuel produced using waste.Microorganisms are also employed in water treatment facilities, biodiesel, and hydrogen gas,a promising sustainable energy source[10].Amirsom et al.[11] presented a mathematical model for three-dimensional bio-convection nanofluid flow along with gyrotactic microorganisms from a biaxial stretching sheet involving the impact of mass slip,thermal jump,and anisotropic slip.Aziz et al.[12]studied the numerical solution of free convection nanofluid flow with gryotatcic microorganisms over a flat plate.The authors conclude that biconvection parameters have significantly impacted the motile microorganisms.Khan et al.[13] investigated a comparison of Williamson and Casson nanofluids flow containing gyrotactic microorganisms.The authors conclude that stratification is dependent on microorganism concentration.

Fluid performance has a significant role in daily life,and it is necessary to study fluid flow motion[14].Many authors did work on nanofluid flow containing gyrotactic microorganisms.Khan et al.[15]studied the natural convection nanofluid flow around a cone that contained gyrotactic microorganisms.The authors concluded that the density number of motile microorganisms,Sherwood number,Skin friction,and Nusselt number enhance along the surface.Khan et al.[16]demonstrated the bioconvection Oldroyd-B nanofluid over a stretched sheet with Prandtl number effects.Waqas et al.[4]investigated the results of a modified second-grade nanofluid over a stretched surface using motile microorganisms.The approximate results were compared to those from previous investigations and found to be very similar.Amirsom et al.[11]analyzed magnetohydrodynamic gyrotactic bioconvection in a square cavity filled with nanofluid.Waqas et al.[17] discussed the approximate solution of micropolar nanofluid across a porous stretching sheet with microorganisms, activation energy, and Nied boundary conditions.Sampath Kumar et al.[18] discussed the bioconvection in magnetofluid containing gyrotactic microorganisms across an elongate plate with a second-order velocity slip.They found that motile microorganisms’boundary layer flow decreased for greater bioconvection lewis and bioconvection number.Sohail et al.[19] investigated the entropy generation in Maxwell nanofluid having microorganisms in the existence of heterogeneous-homogenous reactions.For more studies related to the gyrotactic microorganisms,see[20].

According to the literature,the shape effects of Al2O3on bioconvection nanofluid with gyrotactic microorganisms over the vertical cone in a permeable medium have not yet been reported.The current research aims to examine the shape effect of nanoparticles on bioconvection nanofluid with gyrotactic microorganisms over the vertical cone in a permeable medium.The partial differential equations are converted into ordinary differential equations to find the numerical solutions of the mathematical problem.The results are discussed with graphical illustrations.

The following is the paper’s structure.Section 1 introduces the background and importance of the effect of nanoparticles shape on nanofluid flow.The methodology used in the paper is described in Section 2.The results and discussions are presented in Section 3.The figs are plotted for several values of the parameters.Finally,the study’s conclusion is written in Section 4.

2 Governing Equation

Consider the bio convection Al2O3-water nanofluid flow containing with sphere (spherical)and lamina (non-spherical) shapes nanoparticles and motile microorganisms over the vertical cone in a permeable medium.Furthermore, solutal stratification, heat generation/absorption, chemical reaction, and Joule heating are all phenomena that come with the model.The magnetic field is generated along the y-axis,while the flow is produced parallel to the x-axis,as shown in Fig.1.The equations of the problem are the model as[21]

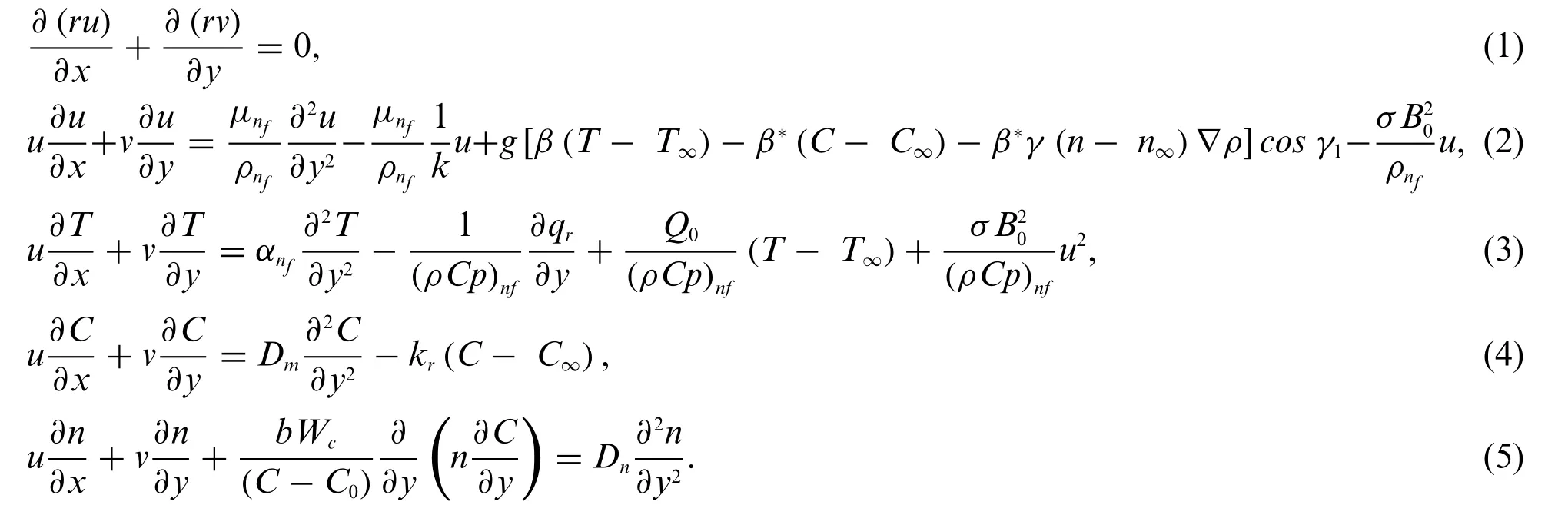
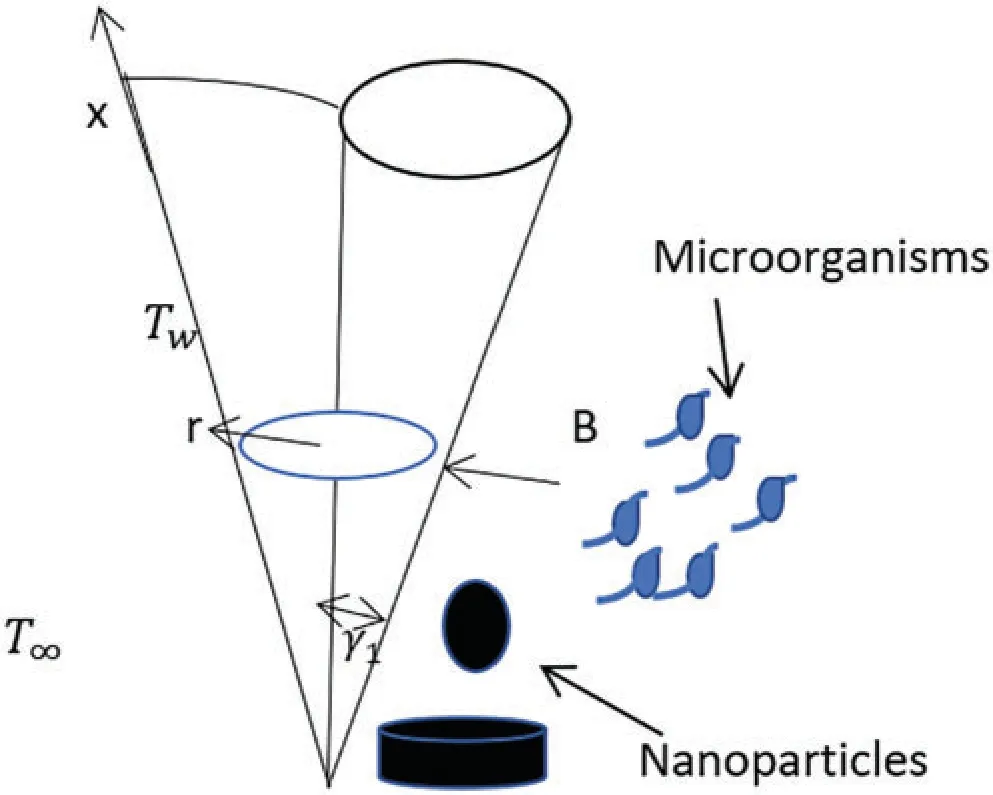
Figure 1:The geometry of the problem

The boundary conditions subjected to the problems are

Hereρnf,μnf,β,β*,B0,γ1,αnf,qr,(ρCp)nf,Dm,Q0,Wc,kr,(e,d),Dn,V0andhfare density,dynamic viscosity, thermal coefficient, solute expansion coefficient, magnetic field strength, cone halfangle, thermal radiation coefficient, modified thermal diffusivity, heat capacity, Brownian diffusion coefficient, heat generation/absorption parameter, maximum cell swimming speed, rate of chemical reaction,reference temperature and concentration dimensionless constants,diffusivity of microorganisms,suction/injection parameter and convective parameter,respectively.

We introduced the similarity transformation variables to non-dimensionalize the above governing equations

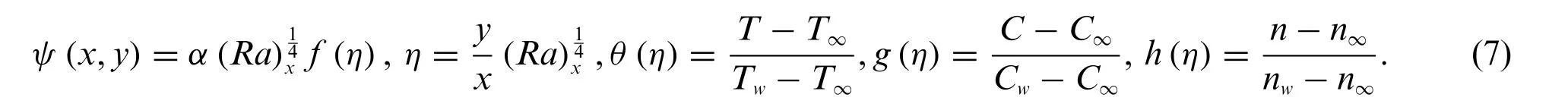
Substituting Eq.(7)into(Eqs.(1)–(5)),we get the following form:

The relevant boundary conditions are described as

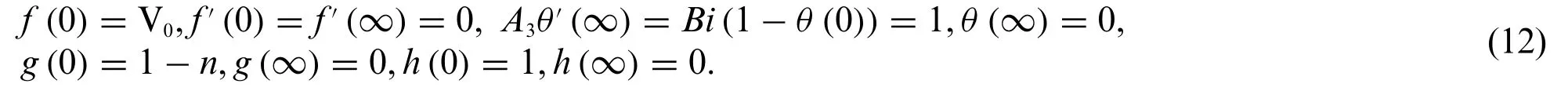
whereK1,M,Rb,Pr,Nr,Rd,Lb,Sc,δ,Cr,Bi,nandPeare present the porous parameter, magnetic parameter, bioconvection Rayleigh number, Prandtl number, buoyancy ratio parameter, Radiation parameter, Lewis number, Schmidt number, Bio convection constant, Chemical reaction parameter,Boit number,solutal stratification,bio convection Lewis number,respectively.In Eqs.(8)–(11),

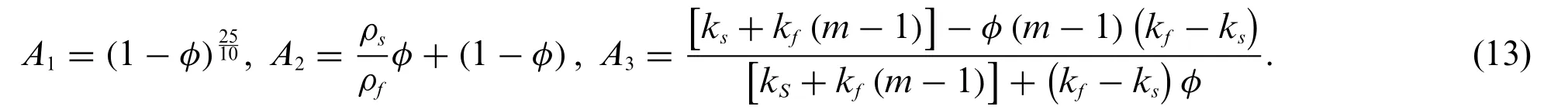
The evaluated physical quantities are

The dimensionless form of evaluated physical quantities is

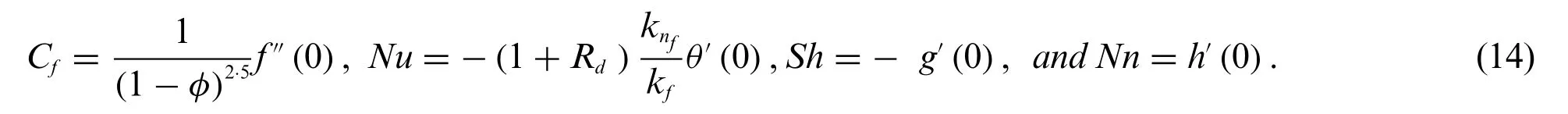
The numerical values of the nanoparticles shape factors (m) are given in Table 1, while the thermophysical properties are tabulated in Table 2.

Table 1:Values of the nanoparticles shape factor(m)as[22]

Table 2:Thermophysical properties of water(H2O)and nanoparticles(Al2O3)as[23]

3 Method

First step of bvp4c converts the higher-order non-linear ODE’s into first order(ordinary differential equations)ODEs,the procedure of bvp4c is following as

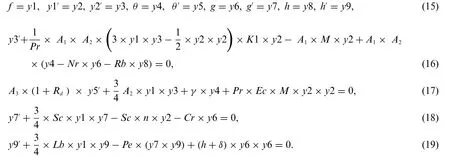
We have introduced(f,f′,θ,θ′,g,h)into(y1,y2,y4,y5,y6,y8)residual form of related boundary value condition as the requirement of MATLAB function.

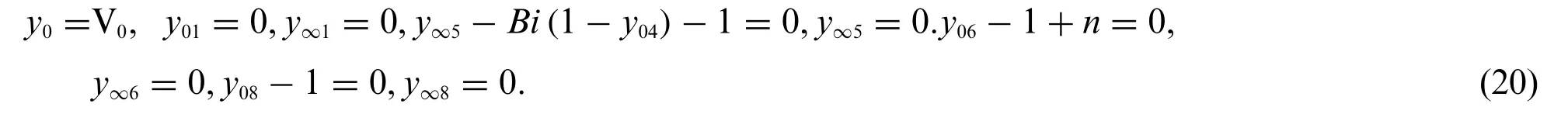
The arguments of MATLAB function are as under.

solinit=bvp4c(linespace(0,infinity,500),Zeros);

options=bvpset(stats,on,RelTol,1e-6);

sol=bvp4c(@ex8ode,@ex8bc,solinit,options).

4 Results and Discussions

The shape effects of nanoparticles are graphically presented in this section.The expressions for velocity and the temperature profiles are calculated numerically by using the bvp4c program.The effects of various physical parameters values on velocity are shown in Figs.2–3.The impact of the magnetic parameter(M)on the velocity profile is depicted in Fig.2.Fig.2 illustrates that the velocity of nanofluid has an inverse relation with magnetic parameter (M).It is also examined that the velocity of sphere(spherical)shape nanoparticles is greater than that of lamina(non-spherical)shape nanoparticles.Fig.3 illustrates the expression of velocity with the effect of the porous parameter(K1).Fig.3 expresses that the velocity of sphere(spherical)shape nanoparticles is greater in a flow system;also,it is noted from Fig.3 that velocity decrease with intensifying the value of the porous parameter(K1).Fig.4 demonstrates the velocity profile with the influence of bio convection Lewis number(Pe).The velocity is shown to decrease as the bio convection Lewis number (Pe) rises, and the velocity of sphere(spherical)shape nanoparticles is higher as compared to the lamina(non-spherical)shape nanoparticles.

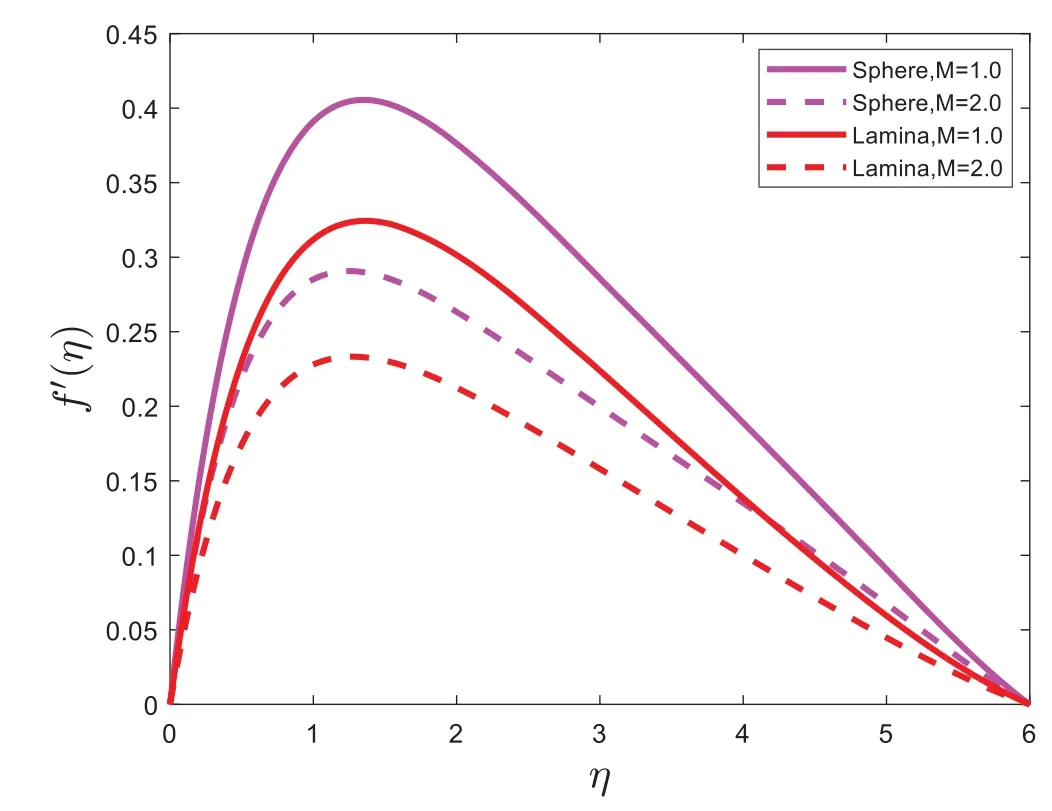
Figure 2:f ′(η)for dissimilar values of M

Figure 3:f ′(η)for dissimilar values of K1

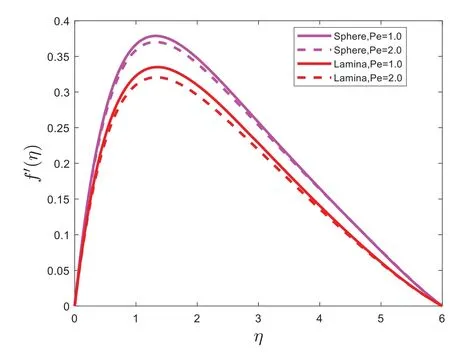
Figure 4:f ′(η)for dissimilar values of Pe

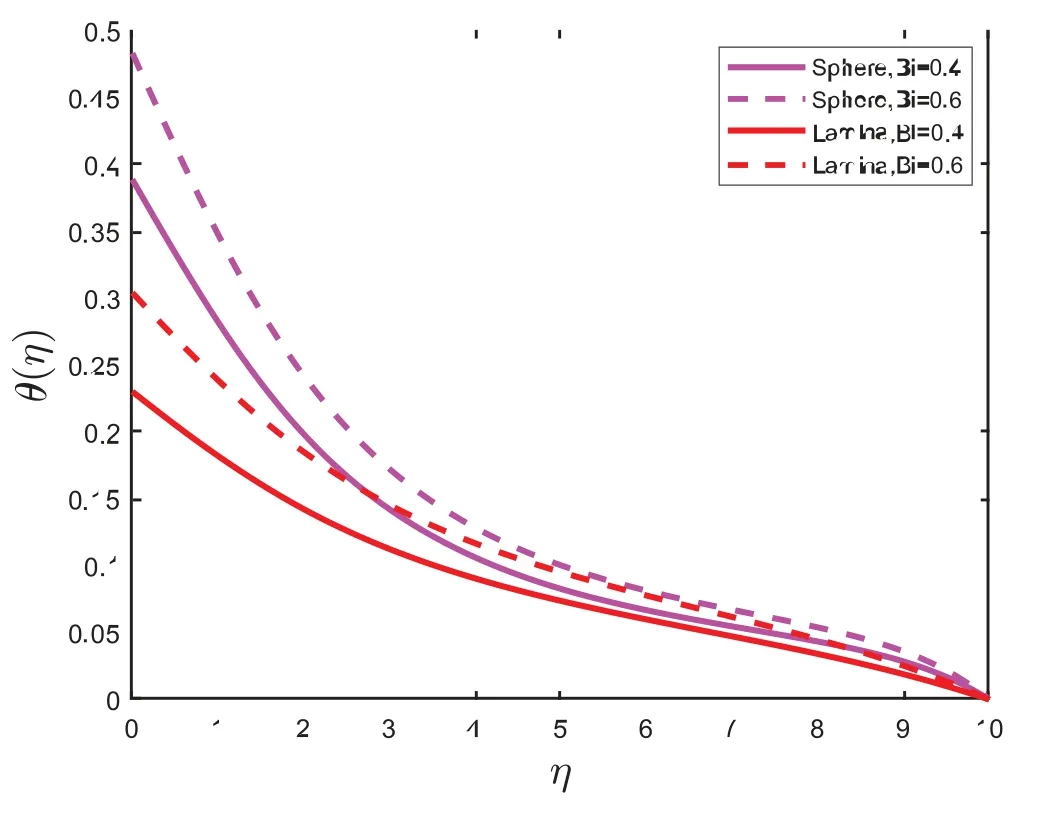
Figure 5:θ(η)for dissimilar values of Bi

The impacts of parameters on temperature profiles are plotted in Figs.5–6.The variation on the nanofluid temperature with the influence of Boit number (Bi)is presented in Fig.5.Fig.5 depicts that the temperature is directly proportional to the Boit number (Bi).The effect of bioconvection Lewis number(Pe)on temperature is plotted in Fig.6.It is witnessed that bioconvection Lewis number(Pe)is an increasing function of temperature.From Figs.5–6, it is noticed the temperature of sphere(spherical)shape nanoparticles is higher as compared to the lamina(non-spherical)shape nanoparticles.The relationship between the Chemical reaction parameter(Cr)and the concentration profile is shown in Fig.7.Fig.7 illustrates that the concentration profile decreases the Chemical reaction parameter (Cr).The impact of solutal stratification(n)on concentration distribution is displayed in Fig.8.It is determined that the concentration distribution decelerates by raising the value of solutal stratification(n).It is found in Figs.7–8 the temperature of lamina(non-spherical)shape nanoparticles is higher as compared to the sphere (spherical) shape nanoparticles.Fig.9 portrays the impact of Lewis number(Lb)on microorganisms’ profiles.Fig.9 shows that the density of microorganisms decreases as the Lewis number(Lb)is increased.Fig.10 displays the effect of bio convection Lewis number(Pe)on the density of microorganisms.It is found that the density of motile microorganisms is reduced when bio convection Lewis number(Pe)is increased.

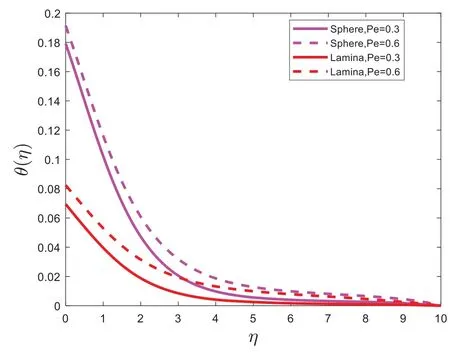
Figure 6:θ(η)for dissimilar values of Pe

Figure 7:g(η)for dissimilar values of Cr

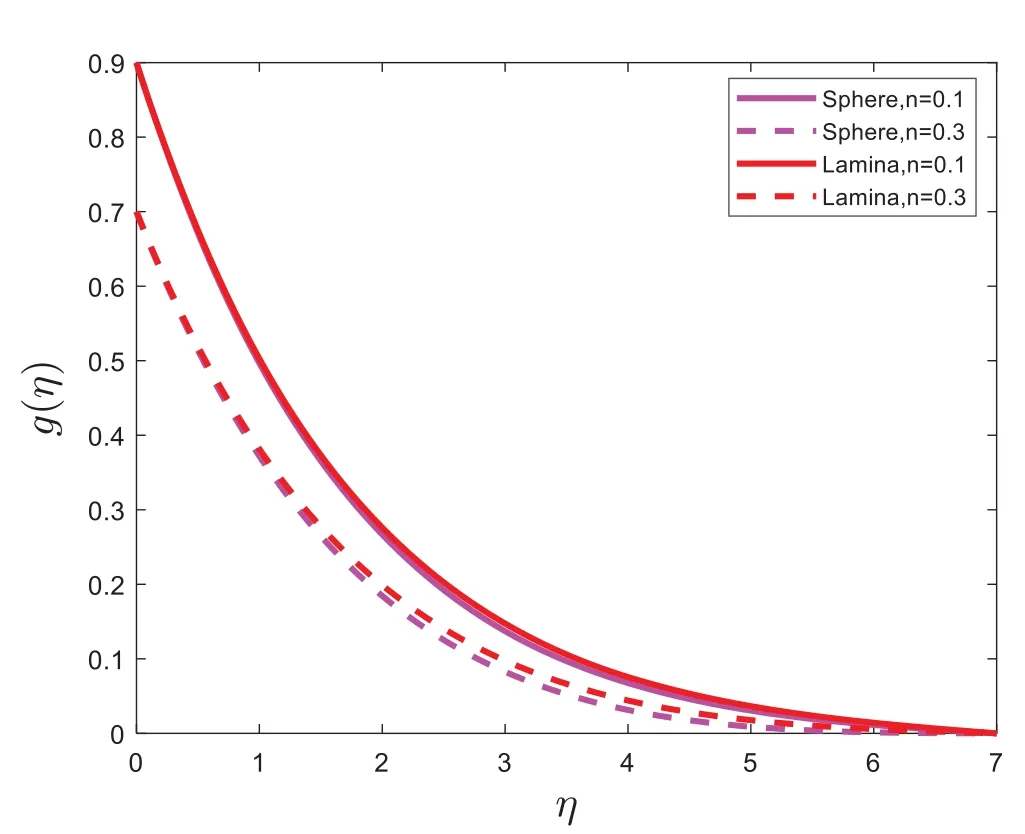
Figure 8:g(η)for dissimilar values of n

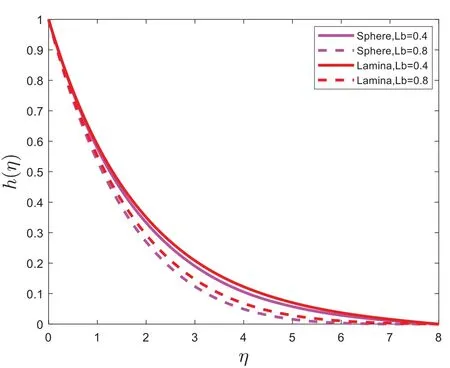
Figure 9:h(η)for dissimilar values of Lb

Figs.11–14 are plotted to explore the behaviors particles shape on skin frictionNusselt number(Nu),Sherwood number(Sh), and Motile density number(Nn)under the influence of bio convection Lewis number(Pe).It is also noticed from Figs.11–12, skin frictionand Nusselt number(Nu)are reduced with intensifying the bio convection Lewis number(Pe), while in Figs.13 and 14,an opposite trend has been found on Sherwood number(Sh)and Motile density numberprofiles.Fig.12 shows that lamina(non-spherical)shape has higher performance in skin frictionprofile.It is also noticed from Figs.11,13 and 14 sphere(spherical)shape nanoparticles have higher performance than the sphere(non-spherical)shape nanoparticles.

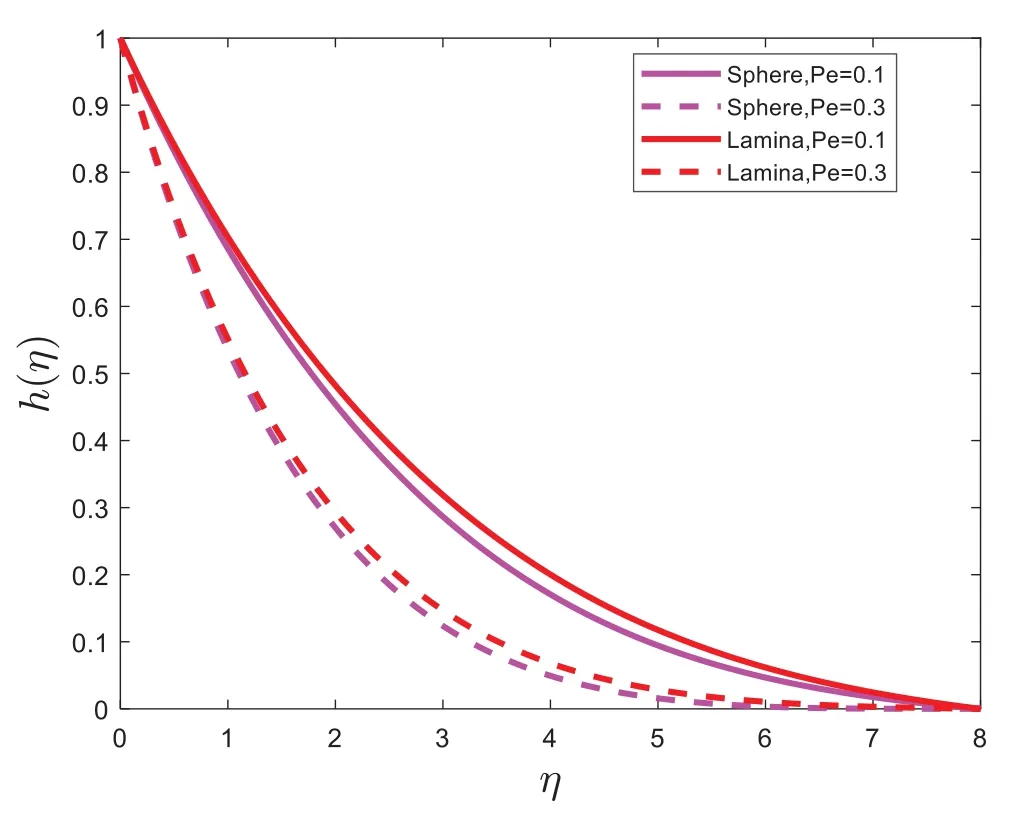
Figure 10:h(η)for dissimilar values of Pe

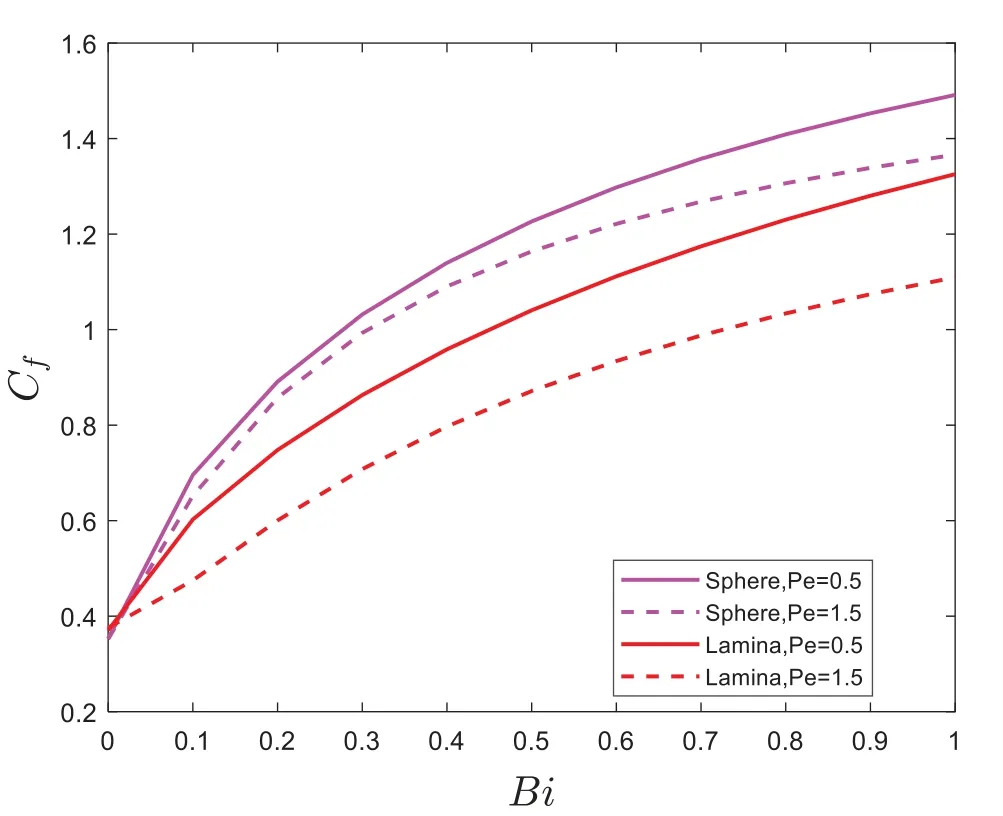
Figure 11:Cf for dissimilar values of Pe

Figure 12:Nu for dissimilar values of Pe

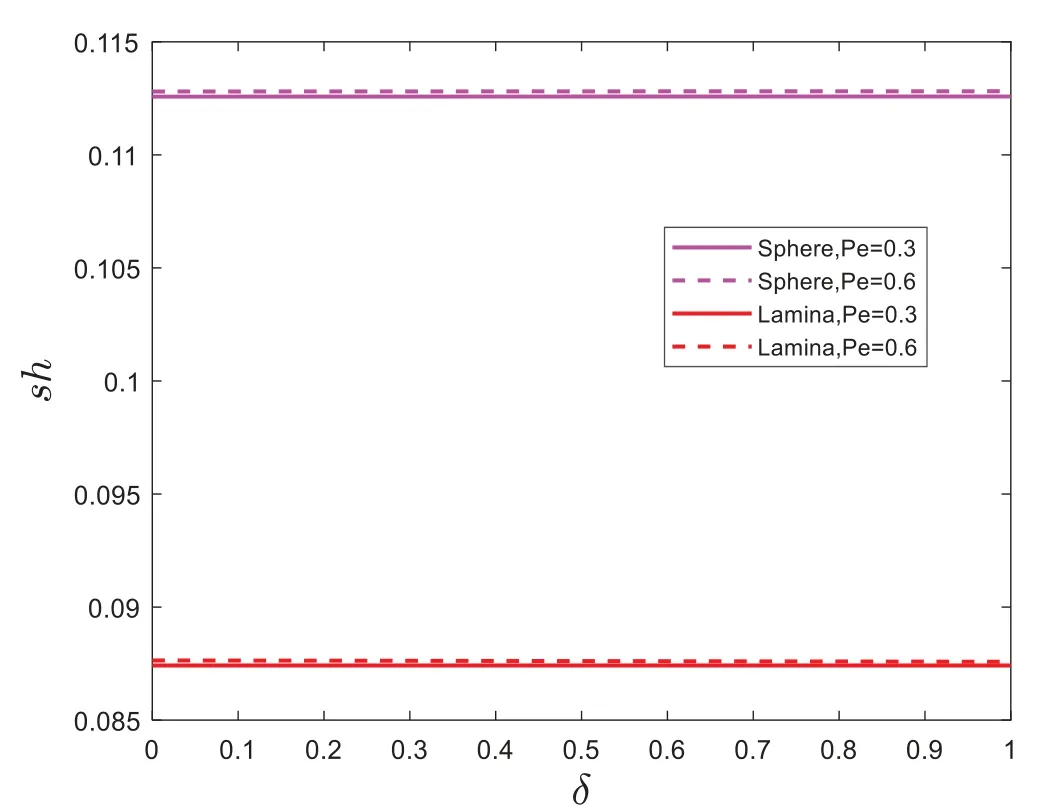
Figure 13:Sh for dissimilar values of Pe

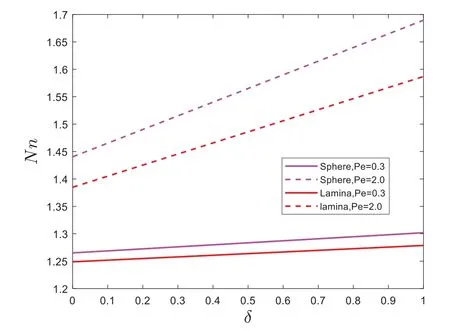
Figure 14:Nn for dissimilar values of Pe

5 Conclusion

This paper studies the effects of nanoparticle shape on nanofluid flow, including gyrotactic microorganisms.The impacts of various parameters on the profiles of motile microorganisms’velocity,temperature,concentration,density,Nusselt number,concentration,Skin friction,and density number of microorganisms are investigated.The points listed below are summarized as follows:

· Velocity profiles of nanofluid decrease for both sphere(spherical)and lamina(non-spherical)shapes nanoparticles.

· Temperature profiles of nanofluid increase for both sphere (spherical) and lamina (nonspherical)shapes nanoparticles.

· Concentration profile and motile microorganisms’ profile are decreased for both sphere(spherical)and lamina(non-spherical)shapes nanoparticles.

· Skin friction and Nusselt number are decreased for both sphere(spherical)and lamina(nonspherical)shapes nanoparticles.

· Sherwood number and Motile density number are increased for both sphere (spherical) and lamina(non-spherical)shapes nanoparticles.

· Sphere(spherical)shapes nanoparticles play a dominant role in the velocity and temperature distribution.

· Lamina (non-spherical) shapes nanoparticles have poor performance in the distribution of velocity and temperature.

· Lamina(non-spherical)shapes nanoparticles play a dominant role on concentration distribution,density of motile microorganisms and Nusselt number.

· Sphere(spherical)shapes nanoparticles have poor performance on concentration distribution,density of motile microorganisms and Nusselt number.

Funding Statement:The authors would like to thank Taif University Researches Supporting Project(TURSP–2020/96),Taif University,Taif,Saudi Arabia,for their financial assistance.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.