Adaptive Fixed-Time Synchronization of Delayed Memristor-Based Neural Networks with Discontinuous Activations

Tianyuan Jia,Xiangyong Chen,2,★,Xiurong Yao,★,Feng Zhao and Jianlong Qiu

1School of Automation and Electrical Engineering, and Key Laboratory of Complex Systems and Intelligent Computing in Universities of Shandong,Linyi University,Linyi,276005,China

2The Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems,and School of Automation,China University of Geosciences,Wuhan,430074,China

ABSTRACT Fixed-time synchronization (FTS) of delayed memristor-based neural networks (MNNs) with discontinuous activations is studied in this paper.Both continuous and discontinuous activations are considered for MNNs.And the mixed delays which are closer to reality are taken into the system.Besides,two kinds of control schemes are proposed,including feedback and adaptive control strategies.Based on some lemmas,mathematical inequalities and the designed controllers,a few synchronization criteria are acquired.Moreover,the upper bound of settling time (ST) which is independent of the initial values is given.Finally, the feasibility of our theory is attested by simulation examples.

KEYWORDS Memristor-based neural networks; fixed-time synchronization; mixed delays; discontinuous activations; adaptive control

1 Introduction

Memristor is nonlinear resistance having memory function, which represents relationship between magnetic flux and charge.Based on the connections between circuits, Chua proposed the existence of it in 1971 [1].The first physical memristor is made by Hewlett-Packard Laboratory in 2008 [2].Unlike ordinary resistors, memristors retain data after a power failure.At present,there are two main applications of memristors:data storage and class brain calculation.Due to the characteristics of small size, low power consumption and fast operation, memristor can be combined with artificial neural networks(NNs) to produce MNNs with more diverse functions and more complex structures.Research on MNNs or NNs have been going on, such as stability [3,4],H∞synchronization [5], FTS [6], Mittag-Leffler synchronization [7] and so on.

Due to the chaotic characteristics of MNNs, it appeared in many fields, such as image protection [8] and random number generation [9].Therefore, the study about synchronization of MNNs is particularly important.Exponential synchronization of MNNs with impulsive and perturbations were put forward by [10], and given a impulsive controller.Li et al.[11] proposed synchronization within finite-time of BAM MNNs and provided a switching control scheme.FTS of MNNs with fractional order was realized in [12] by using a fractional sliding mode control scheme with no singular terms.

In engineering practice, people always expect the system to realize synchronization as soon as possible.Finite time synchronization attracted people’s attention because of its fast error convergence rate and robustness [13,14].Finite-time synchronization can make the error go to zero for a short time.So many of research on finite-time synchronization.Hua et al.[15] used delay-independent controller to settle synchronization of MNNs with inertial item in finite time without using variable transformation while studing from MNNs themselves.Shi et al.[16] put forward finite-time synchronization of Cohen-Grossberg MNNs and divide error into two states.What needs to be noted is that finite-time synchronization is connected with initial value but it is difficult to acquire for large or complex systems.So this is very limited for applications of finitetime synchronization.While, the limitation was solved by FTS which proposed by [17].Different from finite-time synchronization, the ST of FTS is not connected with initial values, which greatly improves the application range of FTS in complex dynamical networks [18] and MNNs.So more and more scholars began to study the FTS of MNNs or NNs in recent years.Based on a new proposed lemma, Li et al.[19] realized the fixed time synchronization problem of coupled NNs,and simultaneously the discontinuity and parameters mismatch of the system were considered.And Ren et al.[20] put forward the FTS of stochastic NNs and got the synchronization criteria.Besides, many achievements about FTS of complex-valued and quaternion-valued MNNs or NNs had also been made in [21,22].

The connection weights of MNNs are switchable, so it belongs to a switching system, which is of great significance to the research of switching systems [23].Meanwhile, it is known that valid control tactics can make the synchronization faster, more stable and easier to meet the needs of practical production applications.Sliding mode control is an effective control method to suppress interference and ensure the stable operation of the nonlinear system [24].Under the sliding model control method, Xiao et al.[25] realized the FTS of NNs.In addition, with the aid of event-triggered algorithm, Bao et al.[26] studied the synchronization of MNNs.Adaptive control is a resultful control schemes [27,28], it has good robustness and has effective suppression of external interference.Especially when the system has unknown parameters and external disturbance, the adaptive control algorithm can track them, so as to ensure the stable operation of the system.Time delay is universal for nonlinear systems.Especially in engineering practice, when the system signal transmission volume is large, it will lead to channel congestion,resulting in discrete time delay, and when there are parallel channels in the signal transmission path, it will lead to distributed time delay.Time delay will affect the stability of the system and hinder the synchronization of the system.In addition, systems with time delay have complex chaotic characteristics and show complex dynamic behaviors, which are very worthy of study.While some previous literatures [6,12,20,25,26] only considered the constant delay or discrete delay but ignored the distributed delay.For NNs, the activation function realizes the nonlinear transformation of data and solves some problems that the linear model cannot solve.Activation functions are mainly divided into continuous and discontinuous types, but discontinuous activation functions are seldom considered by researchers due to the complexity of analysis.

From above discussion, we find that few people have studied FTS of MNNs, especially the case with mixed delays and discontinuous activation functions.Hence, inspired by above conditions, the adaptive FTS of delayed MNNs with discontinuous activations are studied in this study.And our contributions are enumerated in following aspects.(1) Complex MNNs model with mixed delay and discontinuous activations is considered.(2) A feedback control scheme and an adaptive control algorithm are proposed for continuous and discontinuous activations, respectively,and the FTS criterion is obtained.Besides, the results are extended to finite-time synchronization.(3) The ST is not affected by the initial value of system and can be adjusted by the controller and system parameters.

2 Model Formulations and Preliminaries

The drive system of MNNs is

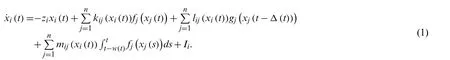
wherex(t)=(x1(t),...,xn(t))T∈Rn,zi ＞0 means rate for ith neuron returns to its idle state andi,j=1,2,...,n.kij(·),lij(·),mij(·) are connection weights.fj(·) andgj(·) are activation functions with or without time delay respectively.Δ(t)delegates discrete time delay and 0 ≤Δ(t)≤Δ1,0 ≤ ˙Δ(t)≤Δ2＜1.w(t)is distributed time delay and 0 ≤w(t)≤w1, whereΔ1,Δ2,w1are constants.Ii(t)is external input vector.The starting condition of (1) isxi(s)=φi(s)∈C([-τ,0],Rn),τ=max{Δ1,w1}.Andwheresignij=1 wheni=j,signij=-1 wheni≠j, andCidenotes capacitor which voltage isxi(t).We define the the memristors betweenanddsandxi(t)areQij,Q′ij,Q′′ijseverally and which resistances arePij,P′ij,P′′ij,respectively.

There exist constantsk′ij,k′′ij,l′ij,l′′ij,m′ij,m′′ij, such that

whereK[A] denotes the convex closure of the setsA,[ε1,ε2] is the convex closure generated by real numbersε1andε2,Ljindicates switching threshold andLj ＞0.Due to the solutions to MNNs are in the sense of Filippov, so set-valued mappings and differential inclusions [29] are used to deal with the discontinuity of MNNs.

Recur to set-valued mappings, it acquires

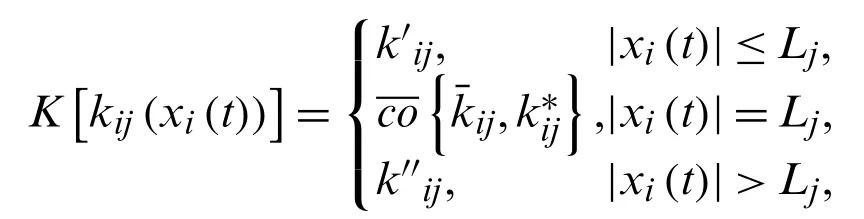
If the activation functions are continuous, one can obtain

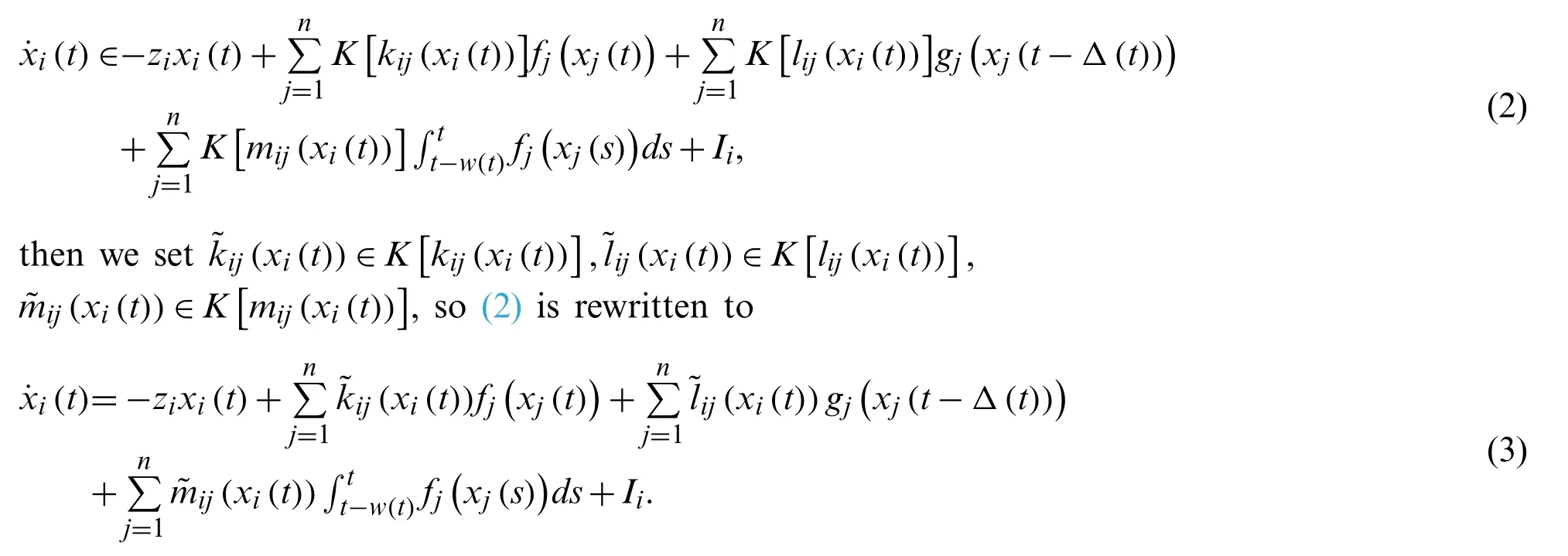
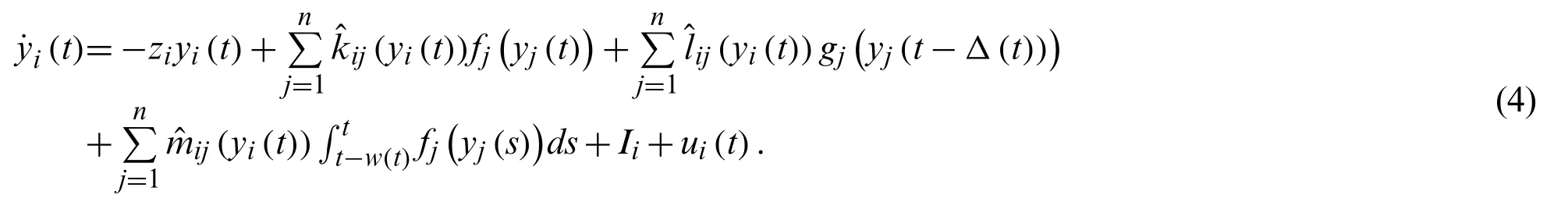
where theui(t)will be introduced below and starting value of (4) isyi(s)=φi(s)∈C([-τ,0],Rn).

The error isei(t)=yi(t)-xi(t), so we have

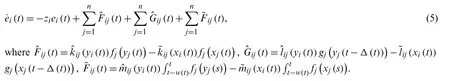
If activation functions are discontinuous, we set

The error is calculated as

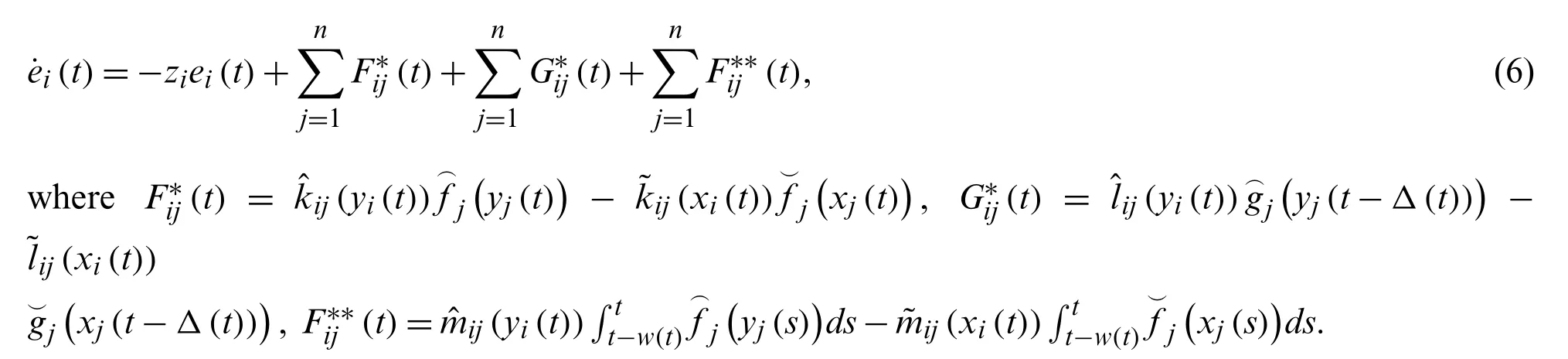
Definition 1.[30] For any original value, the FTS of MNNs will be attained if the ST functionT(e0(s))satifies

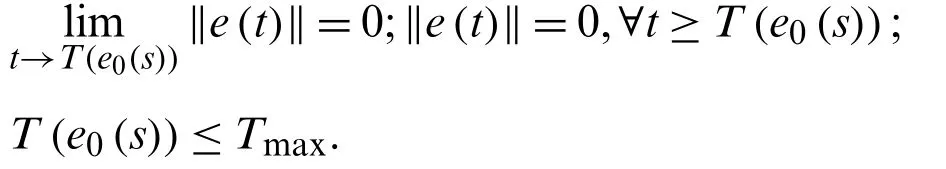
whereTmaxis a constant.

Lemma 1.[31] (1) and (4) will attain FTS if a continuous radically unbounded functionV(·):

Rn→R+∪{0}satifies

(i)V(c)=0 ⇔c=0,

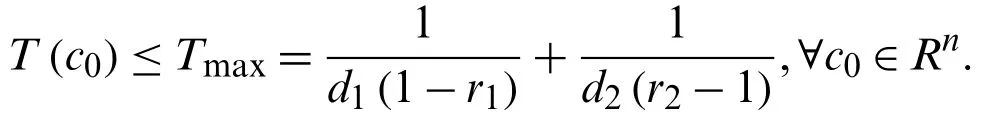
Lemma 2.[32] There are some inequalities as follows:

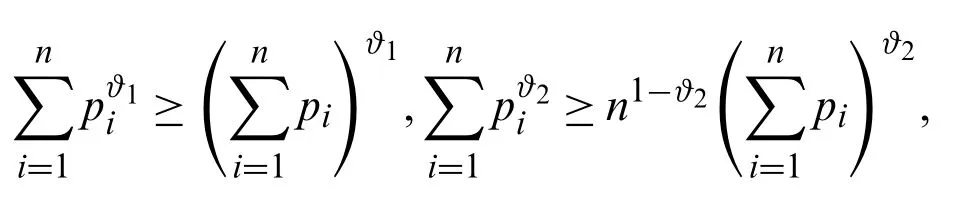
wherepi ＞0,0＜ϑ1≤1,ϑ2＞1.

3 Main Results

The FTS of MNNs with continuous and discontinuous activations will be studied in this section.

3.1 The Continuous Activations for FTS of MNNs

Lemma 3.[33] Ifthe following inequalities are obtained

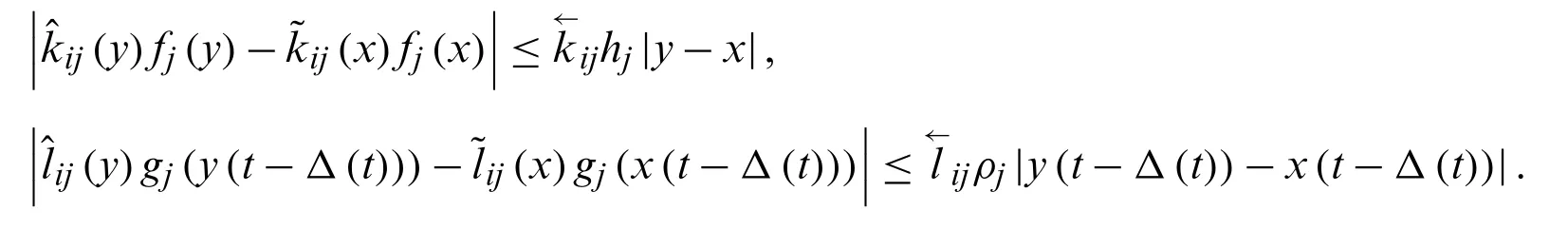
wherehj,ρjare constants.

To realize FTS, control algorithm is given as

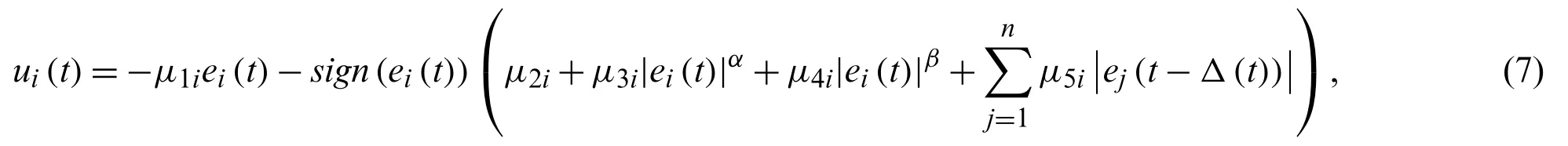
whereμ1itoμ5iare constants,sign(·) is standard sign function and 0＜α ＜1,β ＞1.

Theorem 1.Under the above assumptions and control scheme (7), the FTS of (1) and (4) will be carried out if the following conditions hold

and it can obtain

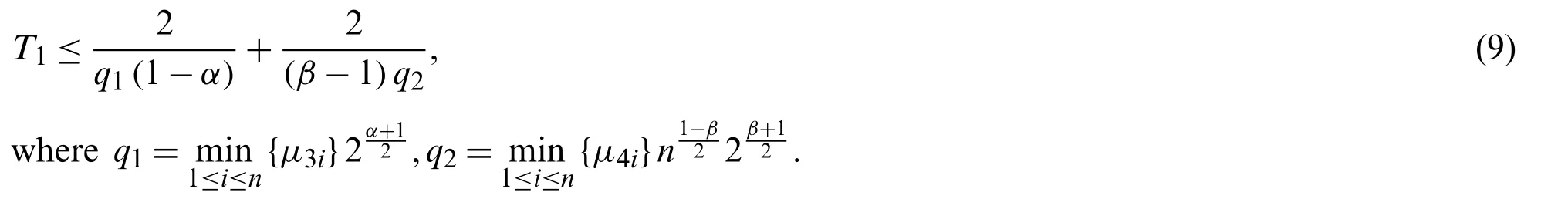
Proof.Construct Lyapunov function as

Along the error system (5), the derivative of (10) can be obtained as

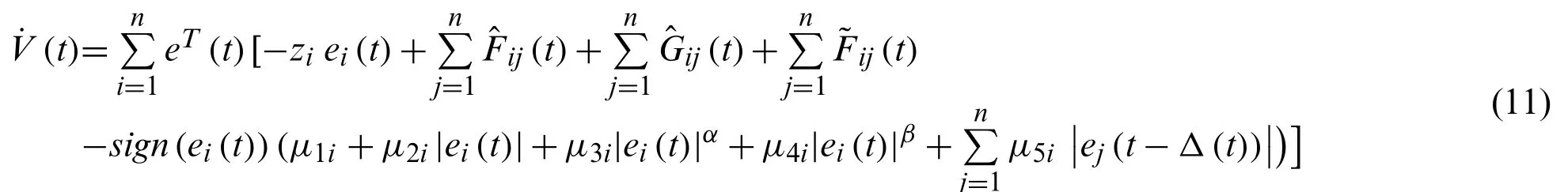
By means of Assumption 1 and Lemma 3, we yield

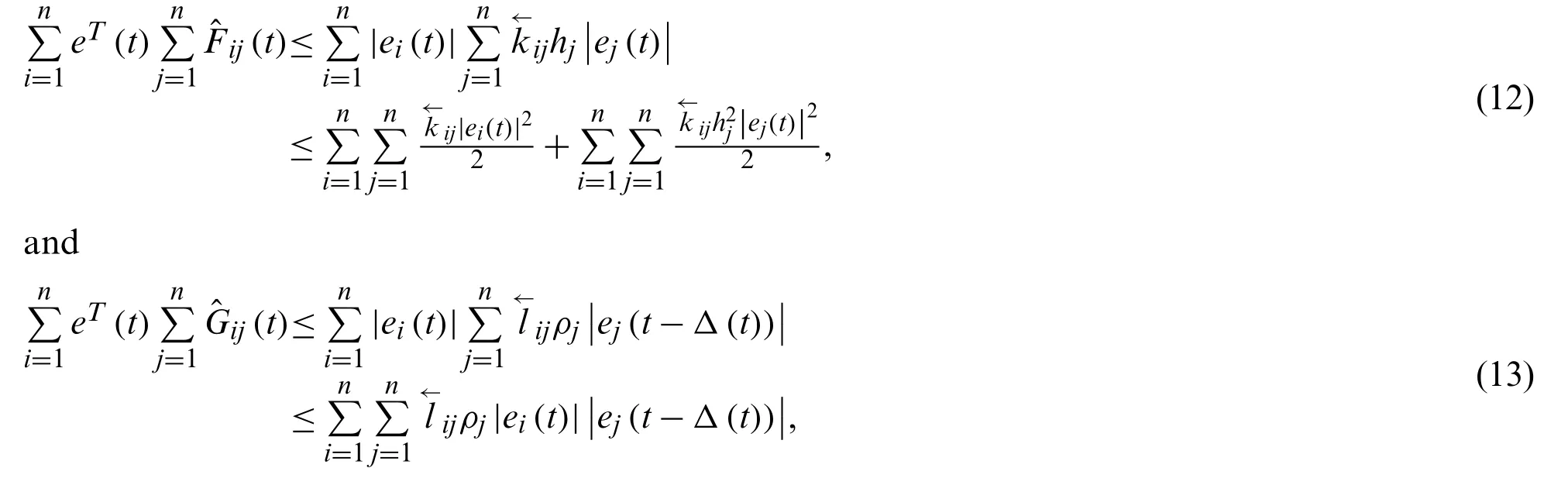
One can also get

Substitute (12)–(14) into (11), we have

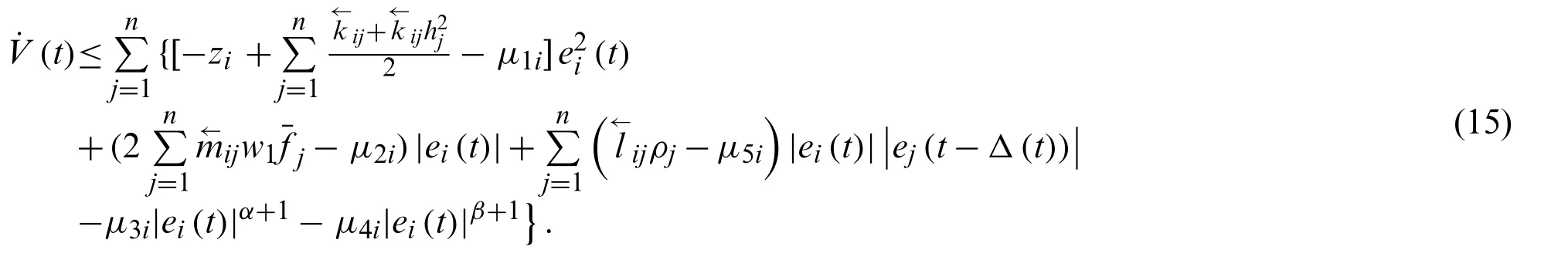
According to Throrem 1 and Lemma 2, it has

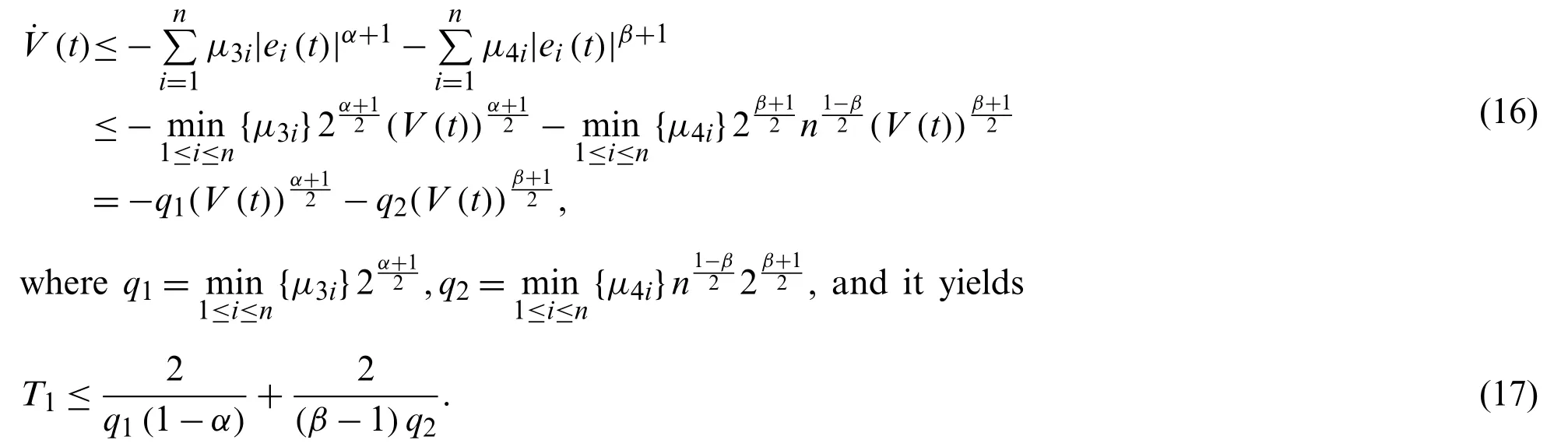
Remark 1.Especially, whenthe ST is expressed as

Corollary 1.Under the below control algorithm, (1) and (4) can reach to finite-time synchronization when Assumption 1 and following conditions hold:

whereκ1itoκ4iare constants and 0＜˜α ＜1, and it can obtain

Remark 2.Unlike the exponential or asymptotic [7–9,27,28] which time to synchronization is long or infinite, the FTS has faster convergence.In addition, the finite-time synchronization[14,26,30] has a fast convergence rate but relies on initial values of the system greatly.However, the starting values of some large and complex systems are hard to know, but FTS overcomes this problem and it can be used widely.

3.2 The Discontinuous Activations for FTS of MNNs

Assumption 1.fv,gv:R→Rare continuous apart from a countable set of ioslate points {θε}.The left limitand right limitoffvexists.Meanwhile, the left limitand right limitofgvexists, and the discontinuous activationssaify

Assumption 2.There are constantsγv,γ′v,ςv,ς′v, such that

According to (6), one can get

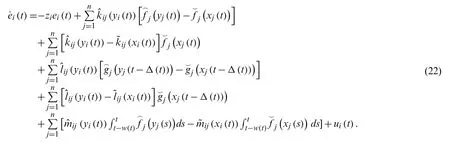
And the nether control adaptive algorithm is designed to ensure the FTS of MNNs.

and adaptive law is

whereξ6i(t)is adaptive gain,ξ1itoξ5iandϖ1are constants.

Theorem 2.FTS with discontinuous activations will be attained under Assumptions 3 and 4 and control (24) if following conditions are met.

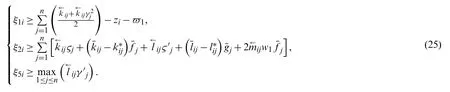
Proof.Choose Lyapunov function as

Take derivative ofV(t)along (25), it acquires

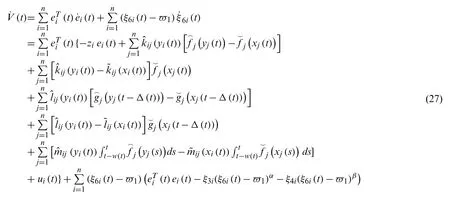
With Assumption 3, it gets

Besides, one can obtain

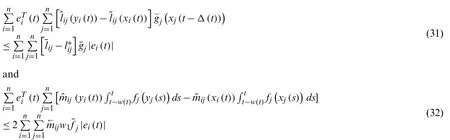
So it yields

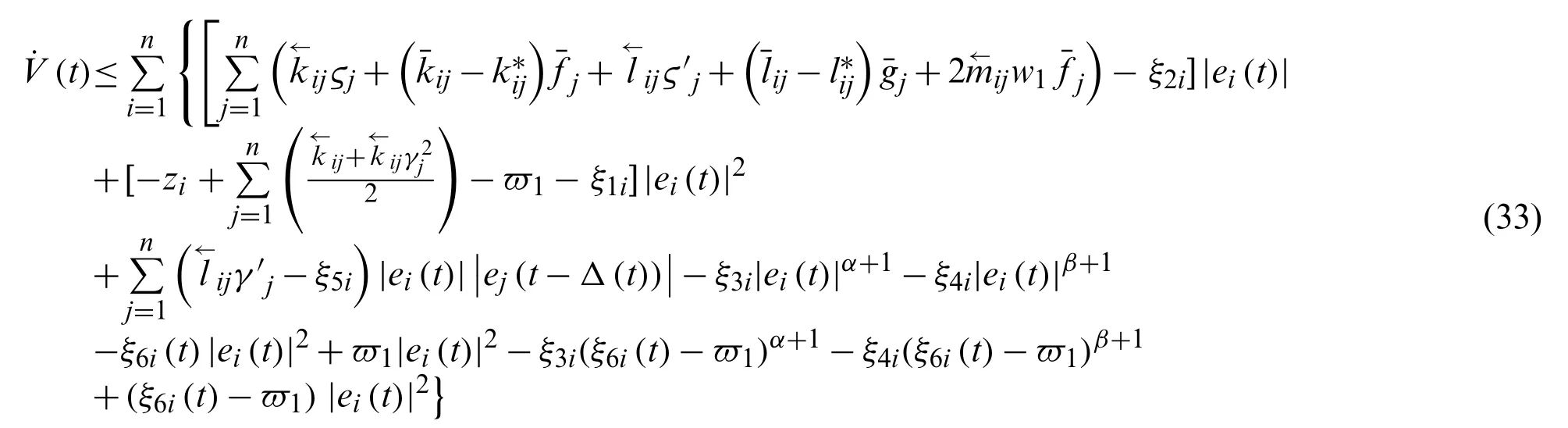
According to Theorem 2, it has

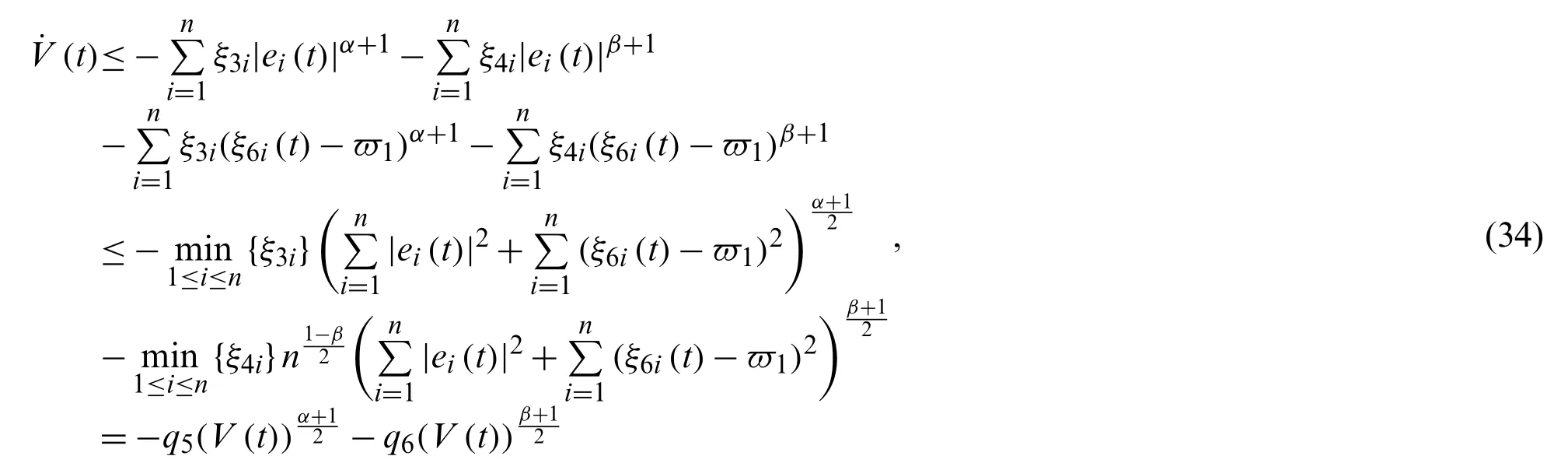
Remark 3.If, it acquires

Corollary 2.Under Assumptions 3 and 4, (1) and (4) attain finite-time synchronization with control scheme (37) if following conditions hold

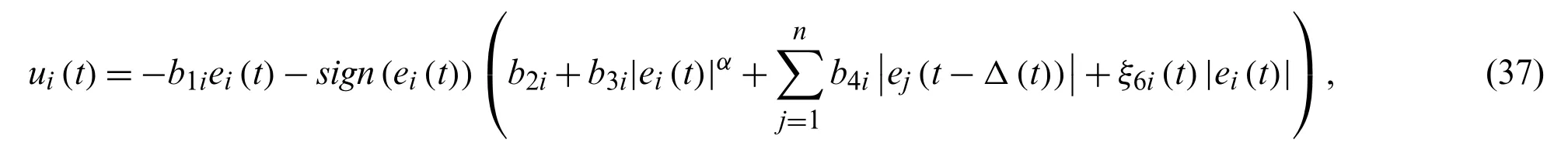
and adaptive law is

and

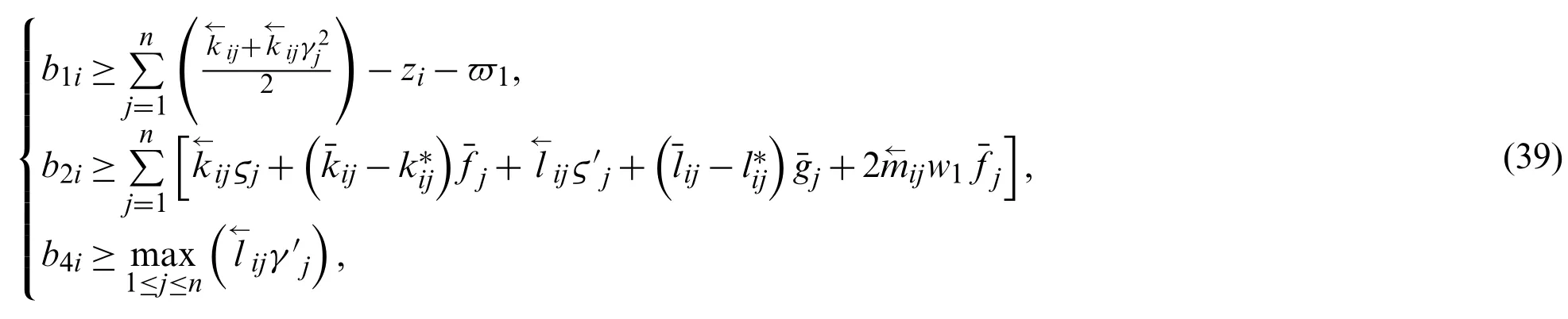
whereb1itob4iare positive constants and 0＜α ＜1 and it acquires

Remark 4.Compared with continuous activation functions [20,25], our study considers the more complicated discontinuous activation functions and mixed delays.Besides, it is known that the gain of feedback control is always larger than the practical application, so the adaptive control are used for FTS in this subjection.The adaptive control has robustness, anti-interference and good suppression effect on external interference, even in the case of some unknown system parameters can also achieve good control effect.

Remark 5.The synchronization criteria of FTS and the upper bound of ST are obtained in our study.Besides, we also derive the relevant criteria for finite-time synchronization, which is more comprehensive than the paper that only studies FTS or finite-time synchronization.From(17) and (35), it’s pretty obvious that ST does not rely on starting values and can be adjusted by changing controller paramaters:μ3i,μ4iandξ3i,ξ4i.

4 Numerical Examples

Examples are offered in this section verifing validity and superiority of above theoretical derivation.

Example 1.This example to verify the FTS of MNNs with continuous activations.

Consider drive system of MNNs with two neurons as

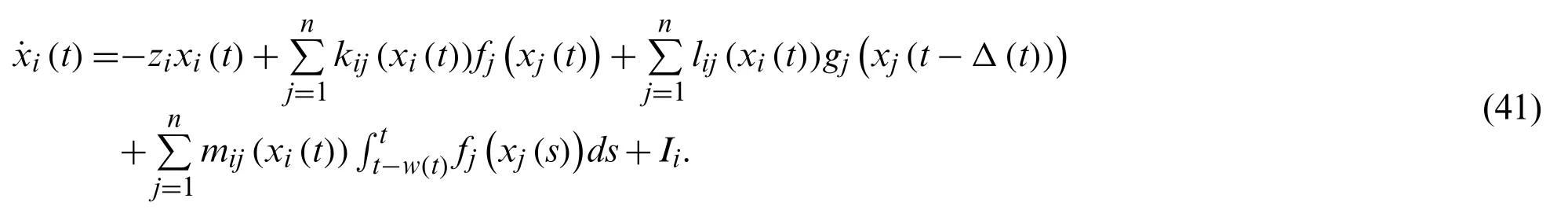
The weighted matrices are

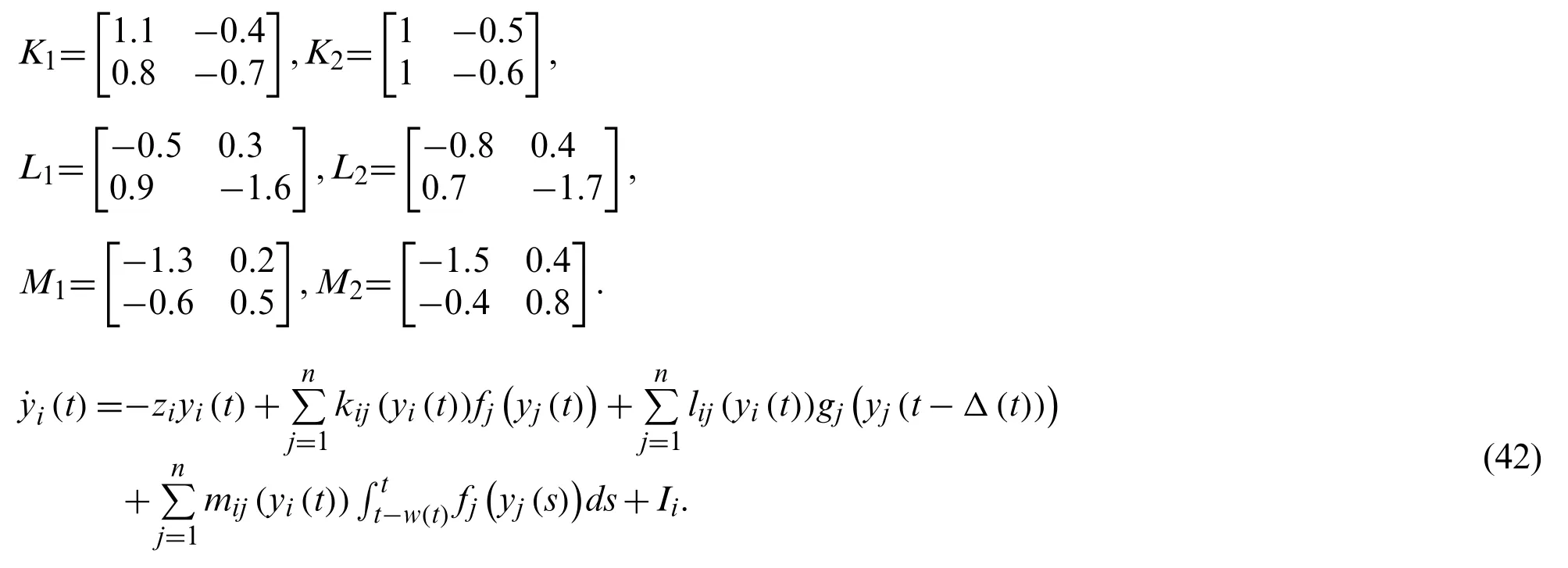
wherei,j=1,2, the switching thresholdLj=1.The delays are set asΔ(t)=sin(t)andw(t)=The starting values are select asxi(t)=[-4,-2]T,yi(t)=[3,2]T.And thefj(·)=gj(.)=tanh(·).

To attain FTS, the parameters are selected asρ1=ρ2= 1,h1=h2= 1,z1=z2= 1,μ11=3.40,μ12= 1.60,μ21= 0.20,μ22= 1.60,μ31= 1.2,μ32= 1,μ41= 1.6,μ42= 1.2,μ51= 1.5,μ52=0.8,α=0.5,β=1.5,¯fj=¯gj=1,w1=1.

The chaotic trajectory with control is showen in Fig.1.Under the action of the controller,the chaotic orbits of the driving systemy1(t),y2(t)finally converge with those of the response systemx1(t),x2(t), that is, the synchronization is realized.The curves of states and errors with control algorithm are exhibited in Figs.2 to 4.The synchronization curves of statesx(t)andy(t)are shown in Figs.2 and 3.It can be seen from the figures that the synchronization of the two states is realized within a finite-time under the action of the control scheme.Fig.4 illustrates that the errorse1(t)ande2(t)approach 0 under the action of the controller, i.e., finite-time synchronization is achieved.

Figure 1:The phase plot of (42) with control

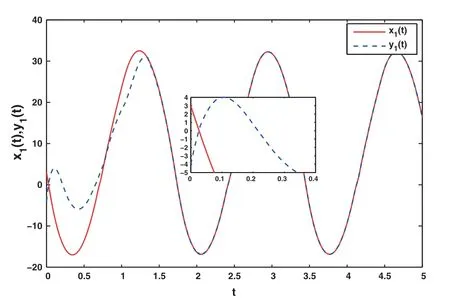
Figure 2:The state diagrams with control

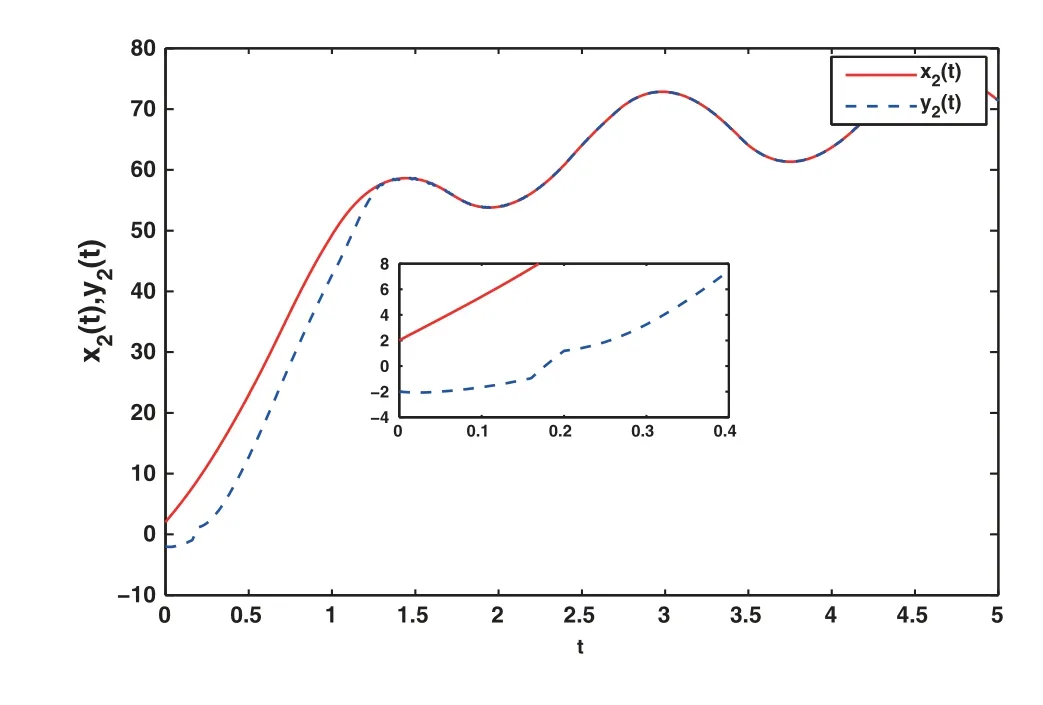
Figure 3:The state diagrams with control

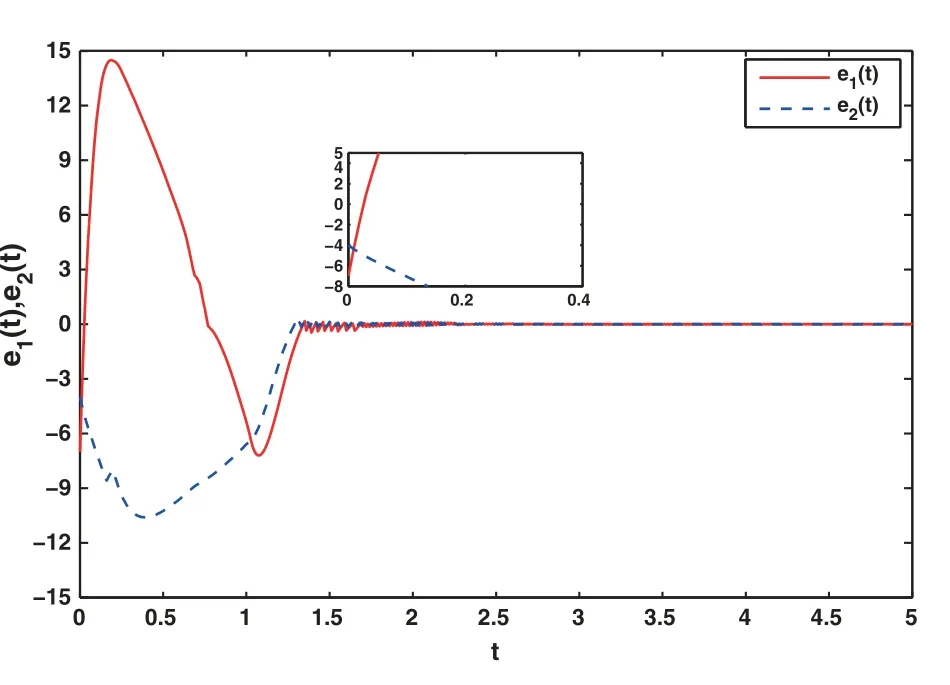
Figure 4:The error graphs with control

Example 2.This example to illustrate the FTS of MNNs with discontinuous activations.

The initial values are set asxi(t)= [-5,-3]T,yi(t)= [5,4]T.And thefj(·) =gj(·) =0.8tanh(·) + 0.04sign(·).The switching threshold and mixed delays are same to example 1.If the controller are added into the error system and the relevant parameters are selected asγ1=γ2=γ′1=γ′2= 0.9,ς1=ς2=ς′1=ς′2= 0.03,ϖ1= 2,ξ11= 3.8670,ξ12= 3.0690,ξ21=-1.4615,ξ22=-1.4615,ξ31=1.5,ξ32=1.7,ξ41=2,ξ42=2.4,¯fj=0.84, and the system can achieve synchronization.The corresponding synchronous plots are shown in Figs.10 to 14.

Fig.5 shows the chaotic trajectory of the driving system, and Fig.6 shows the chaotic trajectory of the response system without the action of the controller.It can be found that the curves in the two pictures are different.The chaos diagram of the response system under the action of the controller can be seen in Fig.10.It can be found that Fig.10 is consistent with Fig.5.

Figure 5:The phase plot of MNNs (41)

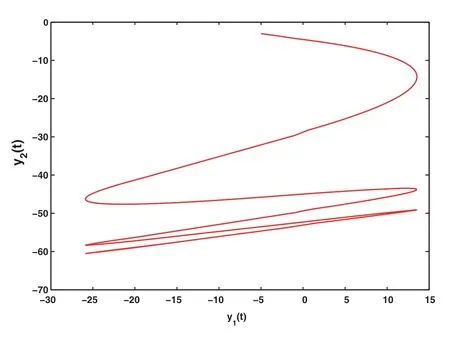
Figure 6:The phase plot of MNNs (42)

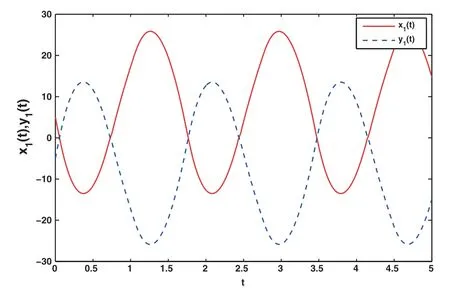
Figure 7:The state graphs without control

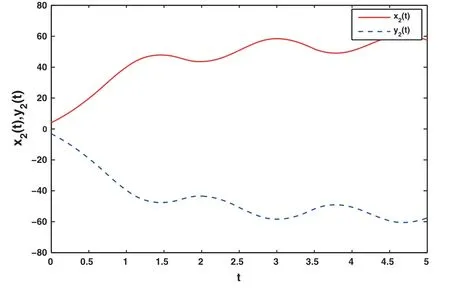
Figure 8:The state graphs without control

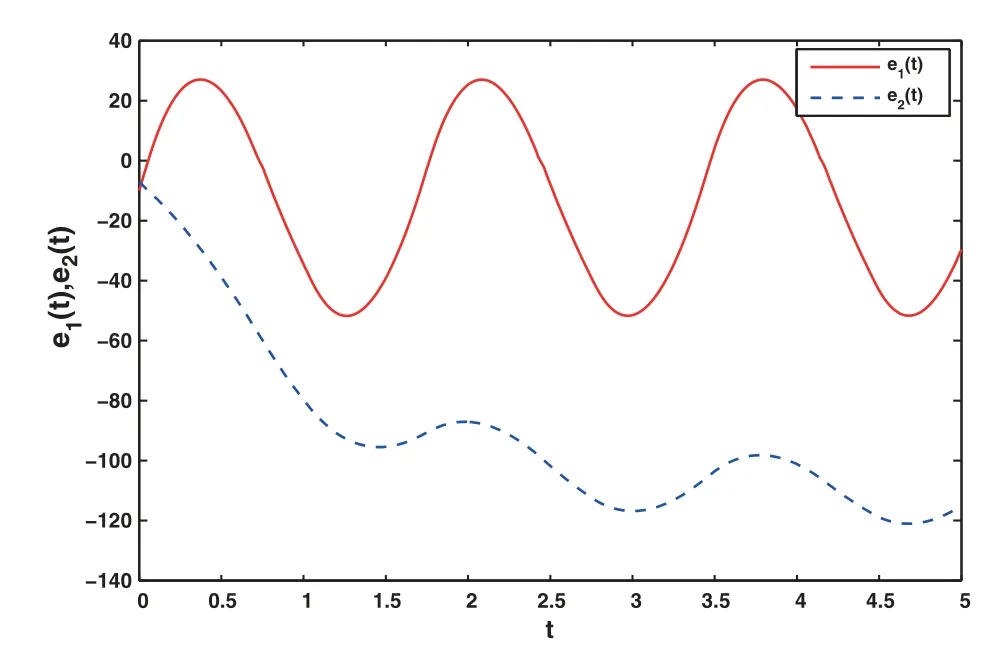
Figure 9:The error graphs without control

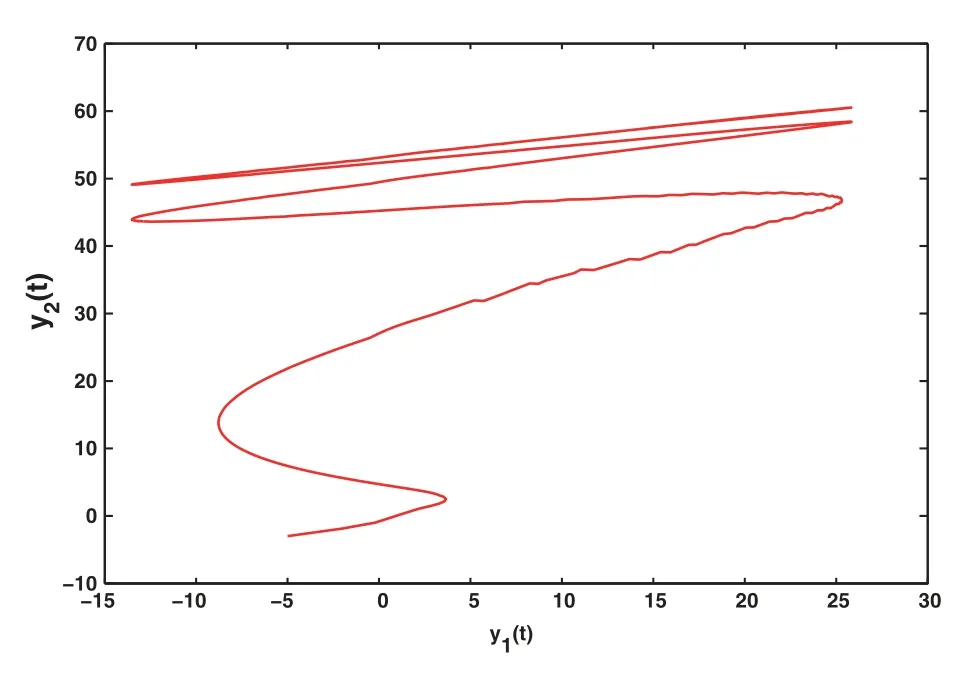
Figure 10:The phase plot of (42) with control

Figs.7 to 9 show the state curves and error curves without the action of the controller.It can be found that the curves are not synchronized.Under the action of the adaptive control algorithm, Figs.11 and 12 show that the state trajectories of the drive and response system realize finite-time synchronization, and Fig.13 shows that the system errors eventually approache to zero.In addition, the evolution curves of adaptive gains for the proposed adaptive control scheme are shown in Fig.14.

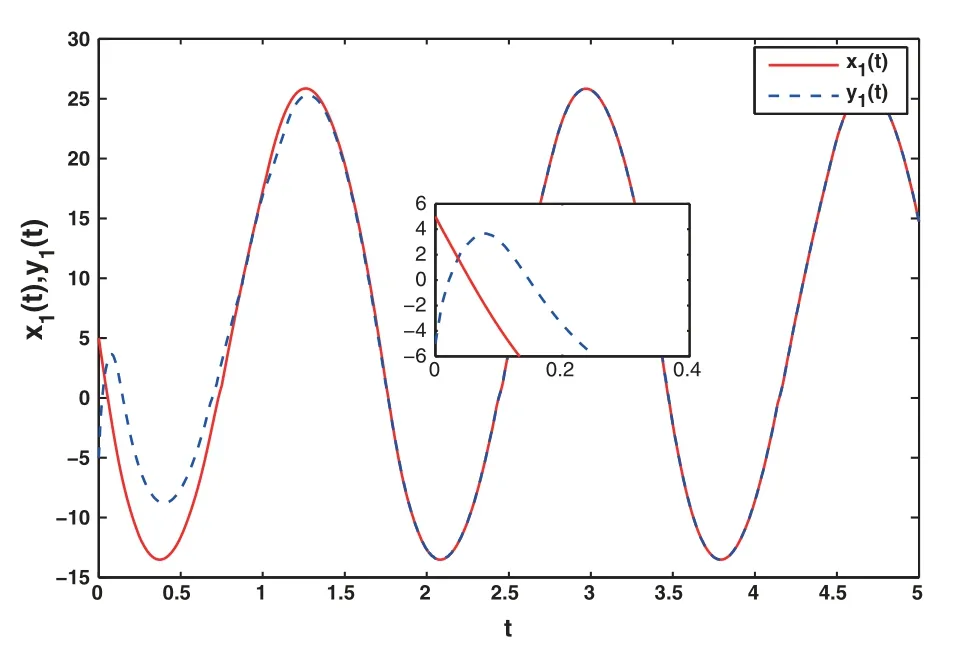
Figure 11:The state graphs with control

Figure 12:The state graphs with control

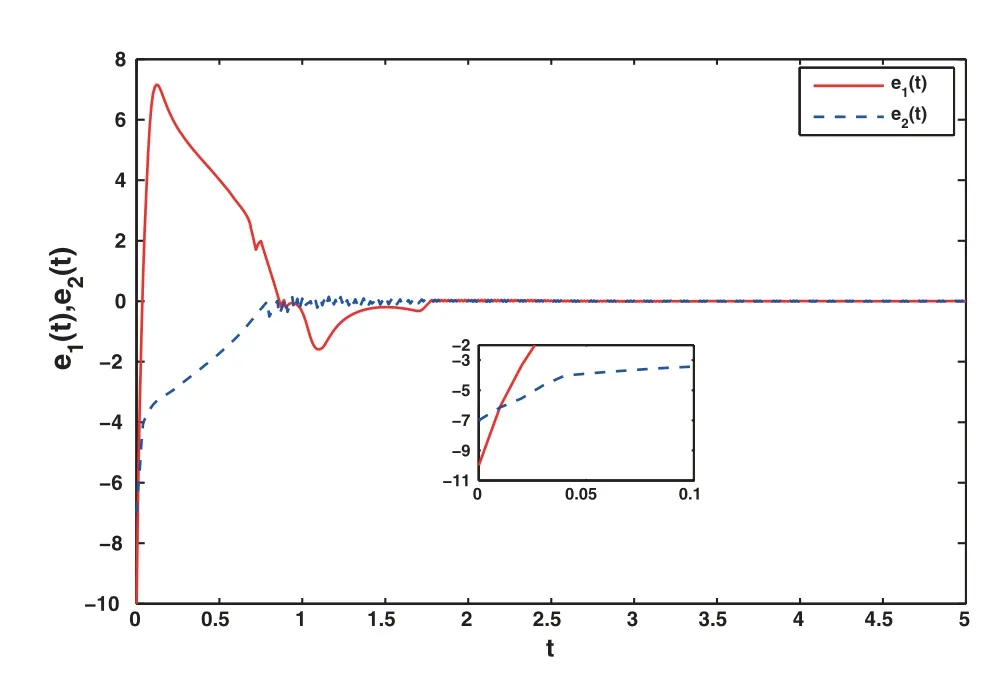
Figure 13:The error graphs with control

Figure 14:The evolutions of adaptive gain

5 Conclusions

The FTS of delayed MNNs with two kinds of activations are discussed.A feedback control algorithm is given for continuous activations and an adaptive control scheme is given for discontinuous activations.Besides, the Filippov theory is used to solove the noncontinuity of MNNs and obtain the synchronization criteria.In addition, through formula derivation, we also draw the conclusion of finite-time synchronization under the same model, so our results are more comprehensive.Finally, two simulation results to prove the feasibility of theoretical derivation.Compared with integer-order MNNs, fractional-order MNNs have more complex dynamic behavior and show stronger chaos.Therefore, the synchronization of fractional-order MNNs are our research direction in the future.

Acknowledgement:The authors would like to thanks the editor office for the deep advice to improve our work.

Funding Statement:This work was supported by National Natural Science Foundation of China under (Grant Nos.62173175, 12026235, 12026234, 61903170, 11805091, 61877033, 61833005),and by 111 Project under Grant B17040, and by the Natural Science Foundation of Shandong Province under Grant Nos.ZR2019BF045, ZR2019MF021, ZR2019QF004, and by the Project of Shandong Province Higher Educational Science and Technology Program No.J18KA354,and by the Key Research and Development Project of Shandong Province of China, No.2019GGX101003.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.