On Fuzzy Conformable Double Laplace Transform with Applications to Partial Differential Equations

Thabet Abdeljawad,Awais Younus,Manar A.Alqudah and Usama Atta

1Department of Mathematics and Sciences,Prince Sultan University,Riyadh,11586,Saudi Arabia

2Department of Medical Research,China Medical University,Taichung,40402,Taiwan

3Centre for Advanced Studies in Pure and Applied Mathematics,Bahauddin Zakaryia University,Multan,60000,Pakistan

4Department of Mathematical Sciences,Faculty of Sciences,Princess Nourah Bint Abdulrahman University,Riyadh,11671,Saudi Arabia

5Centre for Advanced Studies in Pure and Applied Mathematics,Bahauddin Zakaryia University,Multan,60000,Pakistan

ABSTRACT The Laplace transformation is a very important integral transform,and it is extensively used in solving ordinary differential equations,partial differential equations,and several types of integro-differential equations.Our purpose in this study is to introduce the notion of fuzzy double Laplace transform,fuzzy conformable double Laplace transform (FCDLT).We discuss some basic properties of FCDLT.We obtain the solutions of fuzzy partial differential equations(both one-dimensional and two-dimensional cases)through the double Laplace approach.We demonstrate through numerical examples that our proposed method is very successful and convenient for resolving partial differential equations.

KEYWORDS Fuzzy conformable laplace transform;fuzzy double laplace transform;fuzzy conformable double laplace transform;fuzzy conformable partial differential equation

1 Introduction

1.1 Research Background

A natural way to model uncertainty is through fuzzy differential equations[1,2],and[3].Having these models and solutions requires an understanding of the dynamics of design[4].The entire story of humanity relies on this goal,to understand nature.Nowadays,because of various applications of the theory of fuzzy differential equations,many researchers are working on fuzzy partial differential equations.Several researchers emphasized studying the precise/numerical solutions of fuzzy differential equations[5–7].

Various analytical and computational methods can solve fuzzy partial differential equations,see for example [8–12].Integral transform is a very useful technique for solving PDEs and has extensively been used by researchers to solve differential[13].Fuzzy Laplace transform was defined by [14] and then further developed and used by several authors to solve fuzzy ordinary and fuzzy partial differential equations,see for example[15–18].Allahviranloo[19],introduced the conformable Laplace transform,and then developed by several researchers to solve conformable differential equations[20,21].

Recently,Younus et al.[22] generalized two predefined concepts under the name fuzzy conformable differential equations,and got the fuzzy conformable ordinary differential equations under the strongly generalized conformable derivative.For the orderΨ,they used two methods.The first technique is to resolve a fuzzy conformable differential equation into two systems of differential equations according to the two types of derivatives.The second method solves fuzzy conformable differential equations of orderΨby a variation of the constant formula.

In this article,we introduce the double fuzzy Laplace transform in the conformable setting,which is more general than the single fuzzy Laplace transform and we extensively used it in the qualitative theory of fuzzy partial differential equations.

1.2 Research Question

In this paper,we discussed the following questions:

1.In[23]Debnath,provided the solutions of PDEs and Integral and functional equations with double Laplace transform,and Özkan et al.[24],generalized double Laplace transform in the conformable setting.What is the conformable double Laplace transform in the fuzzy environment?

2.What are the forms of fuzzy partial differential equations(both in 1D and 2D)in conformable cases?

3.What are the effects of fuzzy conformable Laplace transformation on the solutions of fuzzy conformable PDEs?

4.What is the application of fuzzy conformable double Laplace transform?Is this transformation providing better results for this application?

1.3 Objective of the Work

A very broad literature including books and papers on the single Laplace transform,its features,and applications are available.However,very few results are available on the double Laplace transform.We generalized the notions of the double Laplace transform in the fuzzy conformable sense.We obtained some basic properties of fuzzy conformable double Laplace.To solve fuzzy conformable partial differential equations,we adopt the fuzzy conformable double Laplace transform.

1.4 Structure of the Study

The organization of this paper is as follows:We present basic principles in Section 2 to use in the main part of the paper.In Section 3,we define the fuzzy double Laplace transform(FDLT),and fuzzy conformable double Laplace transform(FCDLT).Some basic properties of FDLT and FCDLT are also part of Section 3.In Section 4,solutions of the fuzzy conformable partial differential equations are obtained with FCDLT.Concluding remarks are given in Section 5.

2 Basic Concepts

In this section,we recall the basic concepts which we have to use in the major part of the article[14].

A fuzzy set is a mapη:R→[0,1] which generalizes classical sets from {0,1} to [0,1].A fuzzy numberηis a fuzzy set that satisfies some additional properties of convexity,normality,uppersemicontinuity,and compact support.We use RΦto denote the space of all real fuzzy numbers[25].For 0 ≤γ ＜1,γ-cuts for a fuzzy numberηis defined as(η,γ)={v∈R:η(v)≥γ}.Inγ-cuts form,the fuzzy numberηis represented in the form(η,γ)=[(η*,γ),(η*,γ)].A triangular fuzzy numberη,denoted by an ordered triple(a,b,c),with the conditiona≤b≤c.Theγ-cuts associated with triangular fuzzy numberηare[a+(b-a)γ,c-(c-b)γ].

Ifη,υ∈RΦ,then addition on the space of fuzzy numbers byγ-cuts is defined as[(η+υ),γ]=[(η*,γ)+(υ*,γ),(η*,γ)+(υ*,γ)].TheH-difference for two fuzzy numbersηandυdenoted byη⊖υand defined as a fuzzy numberωsuch thatω=η+υ.Inγ-cuts form,H-difference for two fuzzy numbersηandυhas the form [(η⊖υ),γ]=[(η*,γ)-(υ*,γ),(η*,γ)-(υ*,γ)].A fuzzy-valued function with two variablesvandτassigns an ordered pair(v,τ)to a fuzzy numberΦ(v,τ).Inγcuts form,Φ(v,τ)is represented in the formΦ(v,τ.γ)=[Φ*(v,τ,γ),Φ*(v,τ,γ)]([10]).

A fuzzy-valued functionΦ(v,τ)is continuous at any point(v0,τ0)if‖(v,τ)-(v0,τ0)‖＜δ,then we haveΦ(v,τ)-L ＜∈.Mathematically,we can write as

Before defining fuzzy double Laplace transform,we state the fuzzy single Laplace transform and some relevant properties for the fuzzy-valued function of two variables.

Fuzzy single Laplace transform forΦ(v,τ)with respect tovis defined as

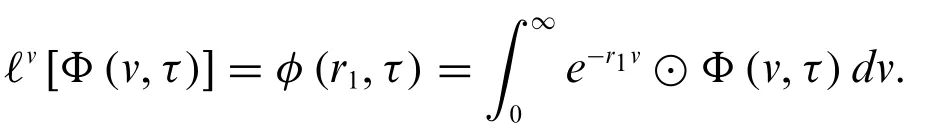
Fuzzy single Laplace transform forΦ(v,τ)with respect toτis defined as[20]

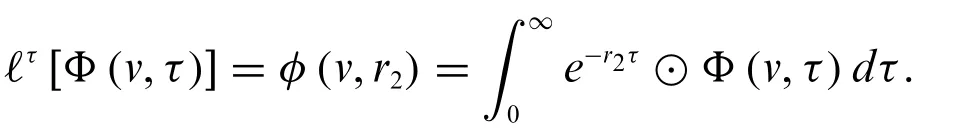
When fuzzy Laplace transform with respect toτis applied to a strongly generalized partial derivative with respect tov,then we have the result

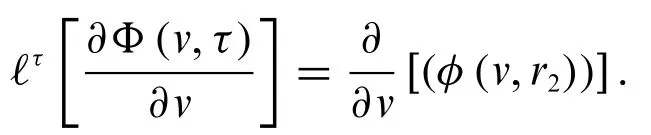
Let us state the translation theorems for fuzzy Laplace transformation:

Theorem 2.1.[14](First translation theorem.)IfΦis fuzzy Laplace transformable,then

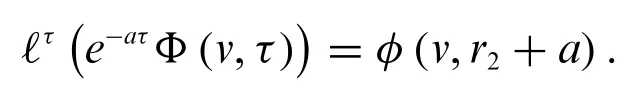
Theorem 2.2.[14](Second translation theorem.)IfΦis fuzzy Laplace transformable,then

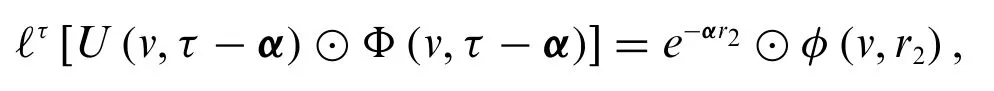
whereUis the Heaviside function.

Theorem 2.3.For a fuzzy-valued functionΦ(v,τ),we have

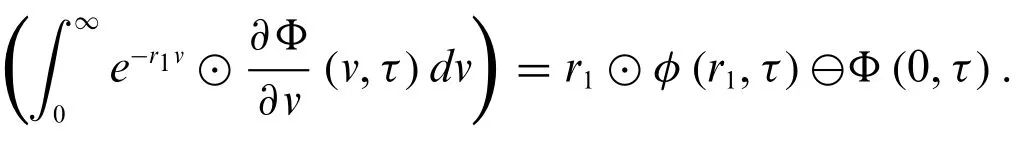
Proof.The proof can easily be done using the integration of parts for fuzzy valued function[10].The following table shows the conformable double Laplace transform for certain functions:

Function Φ(v,τ) Conformable double laplace transform φ(r1,r2)αβ= αβ r1r2.vτ=δ1 δ Ψ1 vΨ τδ Ψγ(1+1 δ)γ(1+ 1 Ψ)r1+1 1 r1+ 1.δ 2 Ψ Ψδ=1 r21r22 vpΨ τqδ.Ψ δ= p!q!r(p+1)1 r(q+1)evΨ Ψ +τδ δ.2=1(r1-1)(r2-1).evΨ Ψ +τδ δ vpΨτqδ(r1-1)p+1(r2-1)q+1.δ,p,q ∈N=p!q!Ψimages/BZ_682_455_1556_486_1601.pngimages/BZ_682_564_1556_595_1601.pngimages/BZ_682_673_1556_704_1601.pngimages/BZ_682_778_1556_809_1601.pngcos λvΨ cos λτδimages/BZ_682_1217_1618_1235_1664.pngλ2+r2=r1r2 Ψ δimages/BZ_682_447_1702_478_1748.pngimages/BZ_682_556_1702_587_1748.pngimages/BZ_682_658_1702_689_1748.pngimages/BZ_682_763_1702_794_1748.pngsin λvΨ sin λτδimages/BZ_682_1536_1618_1554_1664.png.1images/BZ_682_1363_1618_1382_1664.pngimages/BZ_682_1390_1618_1408_1664.pngλ2+r2 2images/BZ_682_1217_1764_1235_1810.pngλ2+r2=λ2 Ψ δ evΨimages/BZ_682_687_1848_718_1894.pngimages/BZ_682_894_1848_925_1894.pngΨ +τδ δ sinhimages/BZ_682_603_1848_634_1894.pngvΨimages/BZ_682_814_1848_845_1894.pngτδ sinhimages/BZ_682_1536_1764_1554_1810.png.1images/BZ_682_1363_1764_1382_1810.pngimages/BZ_682_1390_1764_1408_1810.pngλ2+r2 2 1(r1-2)r1(r2-2)r2.=Ψ δ evΨimages/BZ_682_695_1987_725_2033.pngimages/BZ_682_909_1987_940_2033.pngΨ +τδ δ coshimages/BZ_682_611_1987_641_2033.pngvΨimages/BZ_682_829_1987_860_2033.pngτδ cosh (r1-2)r1(r2-2)r2.= (r1-1)(r2-1)Ψ δ

2.1 Strongly Generalized Conformable Partial Derivatives

In this subsection,we define strongly generalized conformable partial derivative to solve fuzzy conformable partial differential equations.

Definition 2.1.For a fuzzy-valued functionΦ(v,τ),the strongly generalized conformable partial derivative with respect tovis of orderΨis defined as a fuzzy numbersuch that

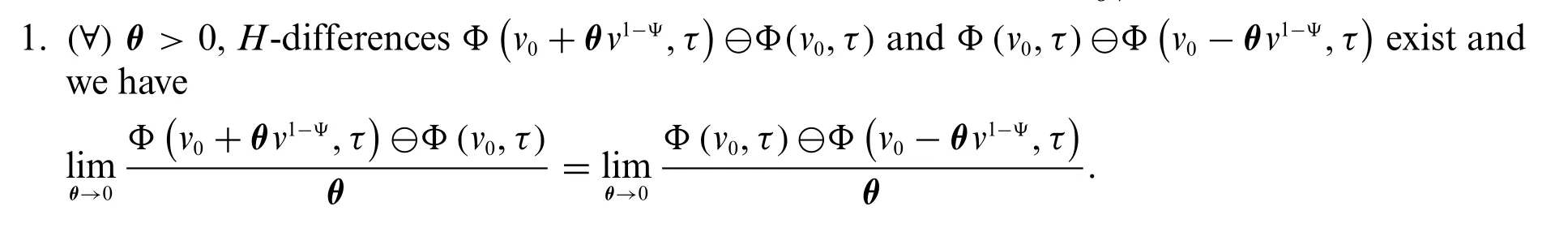
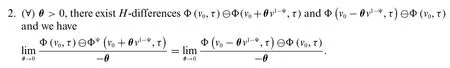
Proposition 2.1.The fuzzy-valued functionΦ(v,τ)is said to be differential of type (Ψ-1) ifΦis differentiable in the first form of the above definition,and differential of type (Ψ-2) ifΦis differentiable in the second form.

Definition 2.2.For a fuzzy-valued functionΦ(v,τ),the strongly generalized conformable partial derivative of orderδwith respect toτis defined as a fuzzy numbersuch that

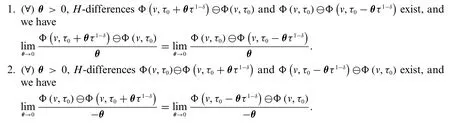
Proposition 2.2.Φis said to be differential of type(δ-1)ifΦis differentiable in the first form,and differential of type(δ-2)ifΦis differentiable in the second form.

For a fuzzy-valued functionΦ,the fuzzy conformable integral of orderΨis defined as

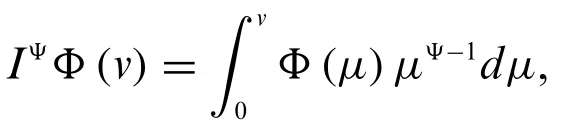
where integration is in the sense of fuzzy Riemann integral.

Lemma 2.1.If a continuous fuzzy-valued functionΦ(v,τ)is strongly generalized conformable partial differentiable with respect toτ,we have

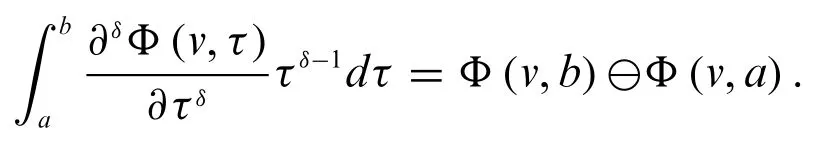
Lemma 2.2.For a continuous fuzzy-valued functionΦ(v,τ)which is strongly generalized conformable partial differentiable,we have

Proof.IfΦ(v,τ)is differentiable of type(Ψ-1),then we have

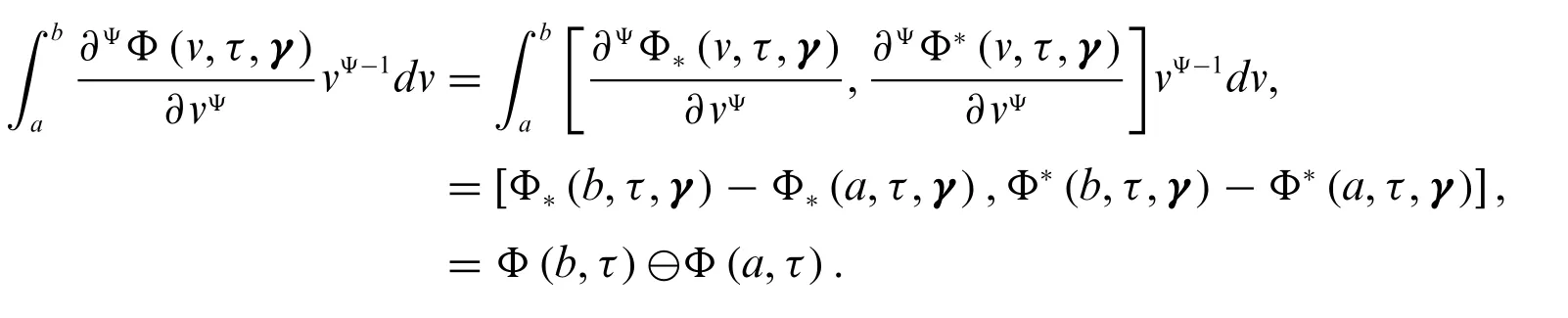
This completes the proof.

3 Double Laplace Transform

Now,we move towards our main results on double Laplace transform.

3.1 Fuzzy Double Laplace Transform

For this,we first define fuzzy double Laplace transform and some related properties.

Fuzzy double Laplace transform of a fuzzy-valued functionΦ(v,τ)is

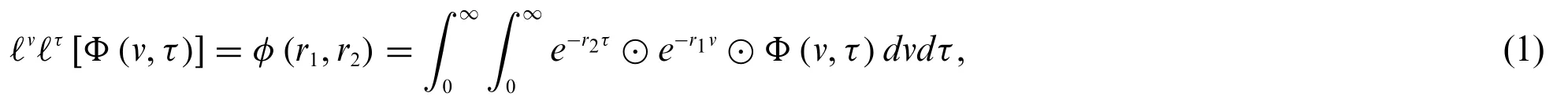
where the integral in the definition should converge.

We can write the above definition in the form

ℓvℓτ[Φ(v,τ)]=[ℓvℓτ[Φ*(v,τ,γ)],ℓvℓτ[Φ*(v,τ,γ)]].

Definition 3.1.Fuzzy double inverse Laplace transform is defined as

Fuzzy double Laplace transform is linear,i.e.,Ifℓvℓτ[Φ(v,τ)]=φ(r1,r2),then for any constantsα,βand fuzzy-valued functionsΦandψ,we have

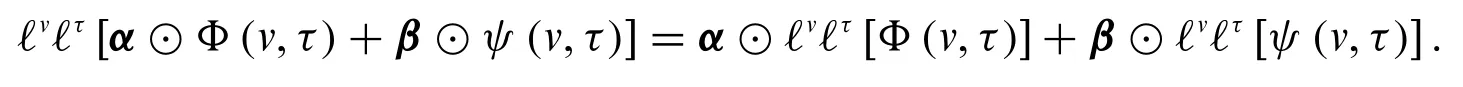
Similarly,the fuzzy inverse double Laplace transform is also linear.

While studying the theory of fuzzy Laplace transform,we have to study the absolute value of the fuzzy-valued function.

Definition 3.2.For the fuzzy-valued funcionΦ,the absolute value of the fuzzy-valued function in theγ-cuts form as

[Φ(v,τ,γ)]=[|Φ*(v,τ,γ)|,|Φ*(v,τ,γ)|].

Definition 3.3.A fuzzy-valued functionΦis called of exponential order in the fuzzy sense if

Φ(v,τ)≤Meαv+βτ,(∀)α,β,M∈R+.

Remark 3.1.Fuzzy double Laplace transform does not exist for all fuzzy-valued functions.For example,Φ(v,τ)=vτ⊙ηorv2+τ2⊙ηis not the fuzzy double Laplace transform of any fuzzy-valued functionΦ(v,τ)becauseΦ(v,τ)does not converge to zero wheneverv→∞,τ→∞.Also,fuzzy double Laplace transform forΦ(v,τ)=exp⊙ηwithα,β＞0 does not exist since it is not of exponential order because

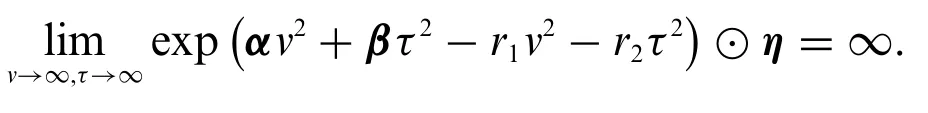
Here we give the condition for the existence of fuzzy double Laplace transform.

Theorem 3.1.If a fuzzy-valued functionΦsatisfies two conditions:

1.Φis of fuzzy exponential order.

2.Φis bounded and piecewise continuous,then fuzzy double Laplace transform exists and also converges absolutely.

Proof.Given isΦis bounded,so we have|Φ(v,τ)| ≤M1.Also,Φhas exponential order,so by definition of exponential order in the fuzzy sense,we have

|Φ(v,τ)|≤M2eαv+βτ,(∀)M2,α,β∈R+.

PutM=max{M1,M2},we obtain

|Φ(v,τ)|≤Meαv+βτ,(∀)α,β,M∈R+.

This yields

Thus we have

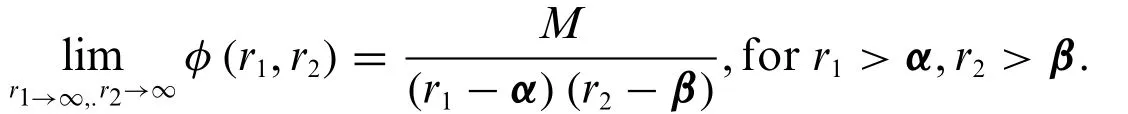
Theorem 3.2.Fuzzy double Laplace transform for a fuzzy-valued functionΦdifferentiable of the first-order is

Case 1:WhenΦis strongly generalized partial differentiable with respect tov,we have

1.IfΦis differentiable of type(1),then

2.IfΦis differentiable of type(2),then

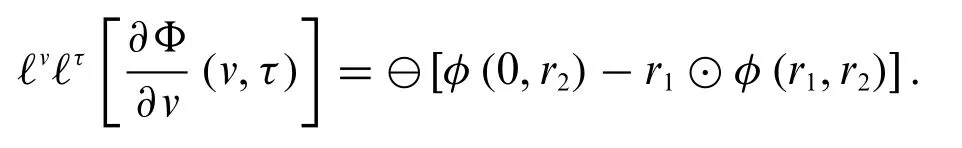
Case 2:WhenΦis strongly generalized partial differentiable with respect toτ,we have

Proof.By using the definition of fuzzy double Laplace transform,we have

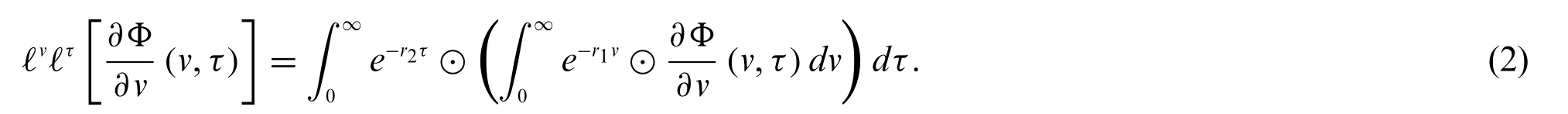
Using Theorem 2.3,we have

Using Eq.(3)in the Eq.(2),we have

This completes our proof.

Theorem 3.3.For second-order fuzzy partial derivative with respect tov,fuzzy double Laplace transform is

Case 1:WhenΦis differentiable with respect tov,we have

1.IfΦandboth are differentiable of type(1),we have

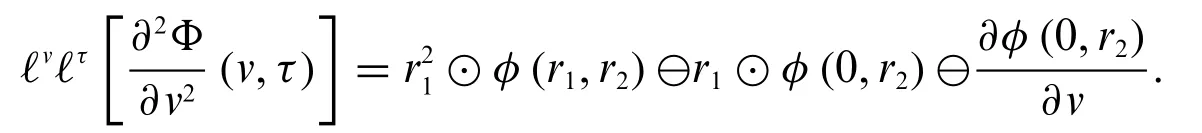
2.IfΦis differentiable of type(1)andis differentiable of type(2),then

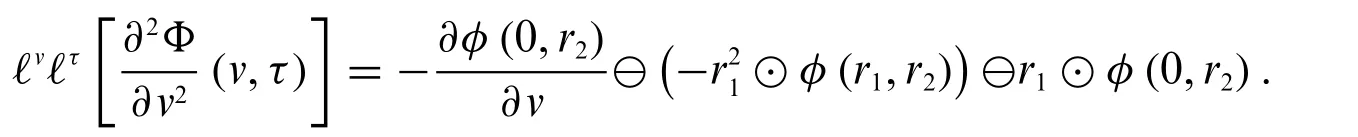
3.IfΦis differentiable of type(2)andis differentiable of type(1),then

4.If bothΦandare differentiable of type(2),we have

Case 2:For second-order partial derivative with respect toτ,double Laplace transform is

1.IfΦand(v,τ)both are differentiable of type(1),we have

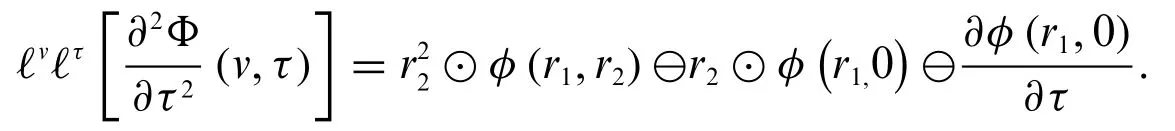
2.IfΦis differentiable of type(1)and(v,τ)is differentiable of type(2),then

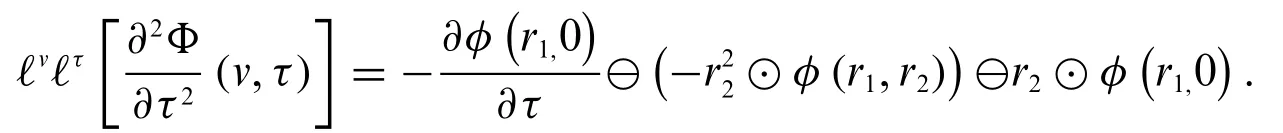
3.IfΦis differentiable of type(2)and(v,τ)is differentiable of type(1),then

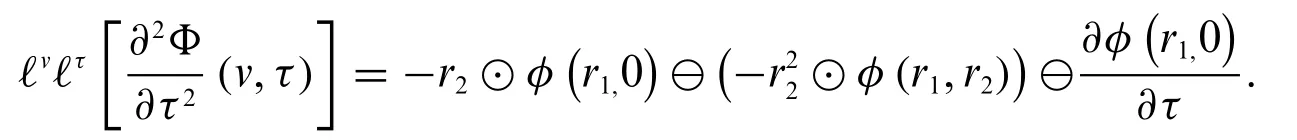
4.IfΦand(v,τ)both are differentiable of type(2),we have

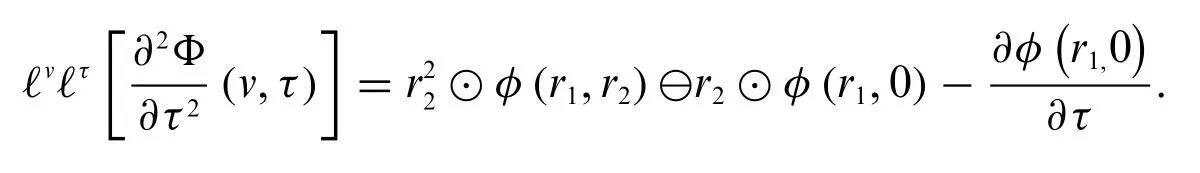
Theorem 3.4.For a fuzzy-valued function differentiable with respect tovandτ,fuzzy double Laplace transform is

1.WhenΦ(v,τ)is differentiable of type(1)with respect tovandτ,we have

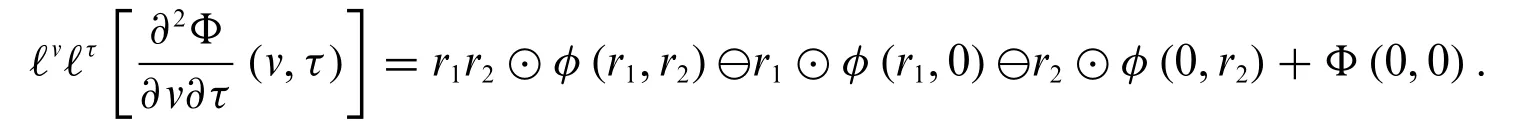
2.WhenΦ(v,τ)is differentiable of type(2)with respect tovandτ,we have

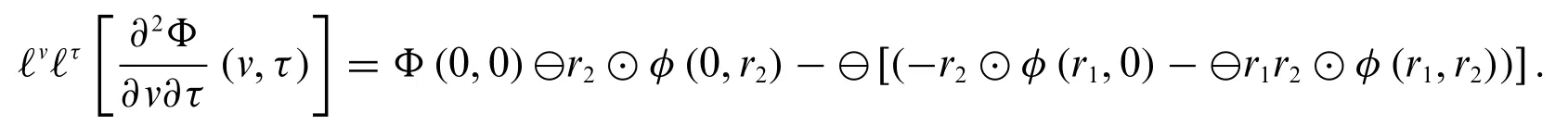
3.WhenΦ(v,τ)is differentiable of type(1)with respect tovand differentiable of type(2)with respect toτ,we have

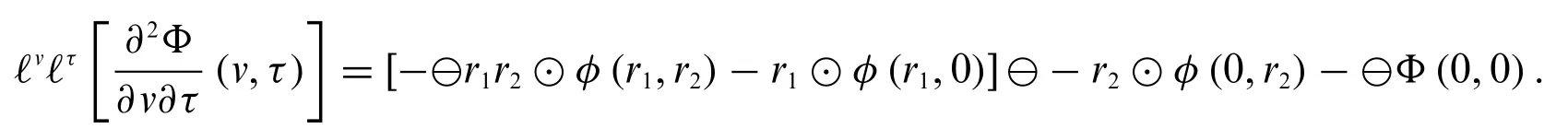
4.WhenΦ(v,τ)is differentiable of type(2)with respect tovand differentiable of type(1)with respect toτ,we have

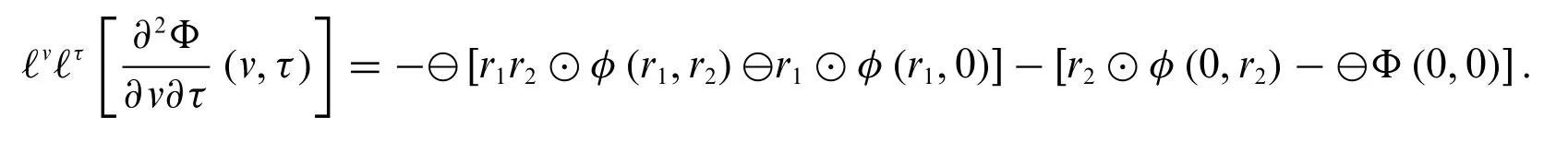
Proof.We provide proof for case(2)here.Other cases are similar.

SinceΦis differentiable of type(2)with respect tov,then

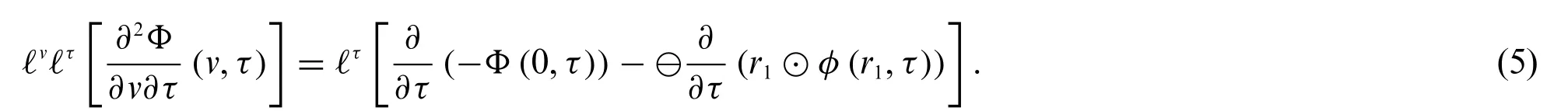
Now,apply the Laplace transform forτ,we have

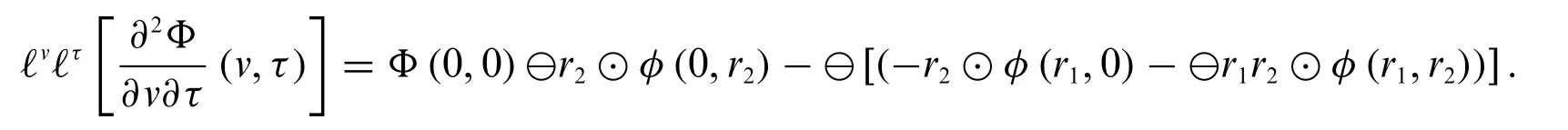
This completes the proof.

Theorem 3.5.For a fuzzy-valued function,whose fuzzy double Laplace transform exists,we have

Proof.Using the definition of fuzzy double Laplace transform,we have

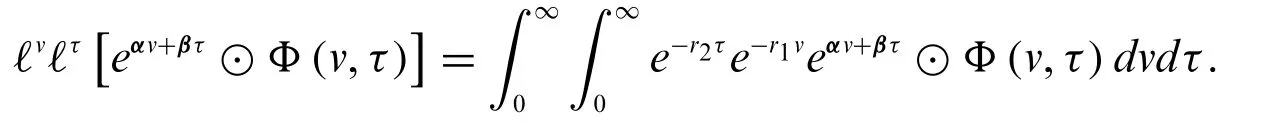
This results in

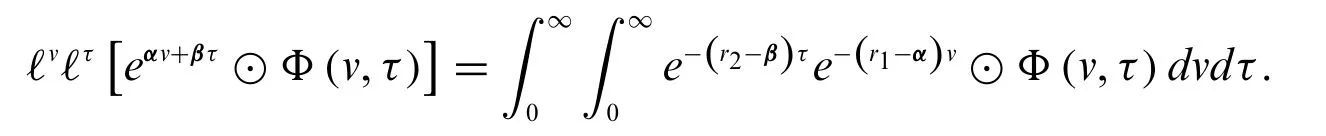
Thus,we obtain our required result.

Theorem 3.6.For a fuzzy-valued function,whose fuzzy double Laplace transform exists,we have

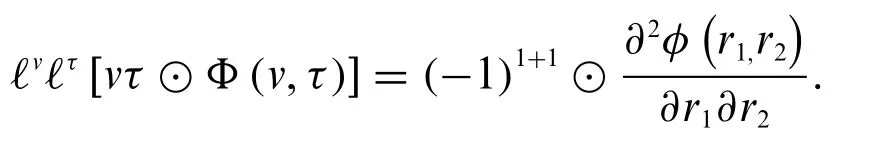
Proof.If we take the strongly generalized partial derivative with respect tor1andr2,we have

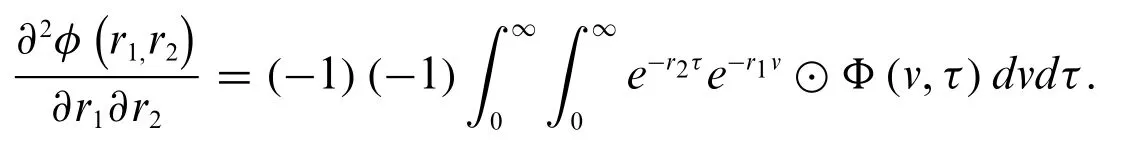
This can be written as

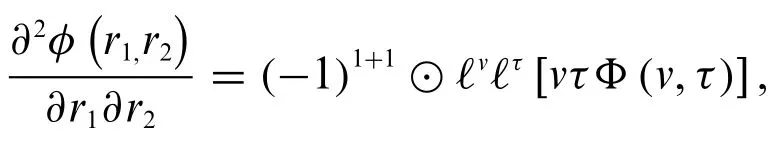
or we can write

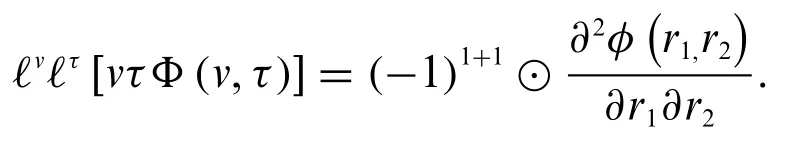
In general,we have

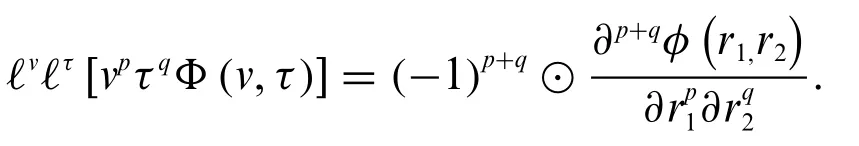
Theorem 3.7.(Second translation theorem).For a fuzzy-valued function,whose fuzzy double Laplace transform exists,the second translation theorem in the fuzzy sense has the form

ℓvℓτ[Φ(v-η,τ-μ)⊙U(v-η,τ-μ)]=e-r1η-r2μ⊙φ(r1,r2),

whereU(v,τ)is the Heaviside unit step function defined by

U(v-η,τ-μ)=1,whenv＞η,andτ＞μ,

U(v-η,τ-μ)=0,whenv ＜ηandτ ＜μ.

Proof.Using the definition of fuzzy double Laplace transform,we have

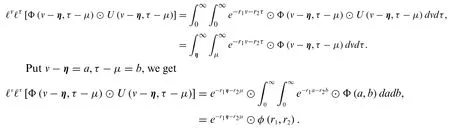
Definition 3.4.IfΦ(v,τ)is a fuzzy-valued function andψ(v,τ)is a real-valued function,then convolution in fuzzy sense is defined as

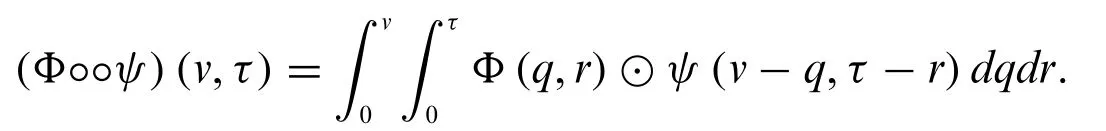
Theorem 3.8.For fuzzy double Laplace transform,the Convolution theorem is given by

ℓvℓτ[(Φ°°ψ)(v,τ)]=ℓvℓτ[Φ(v,τ)]⊙ℓvℓτ[ψ(v,τ)].

3.2 Fuzzy Conformable Double Laplace Transform

Now,we generalized the concept of fuzzy double Laplace transform to fuzzy conformable double Laplace transform.

Definition 3.5.Fuzzy conformable double Laplace transform for a fuzzy-valued functionΦ(v,τ)is

where the integral in the definition should converge.

We can write the above definition in the form

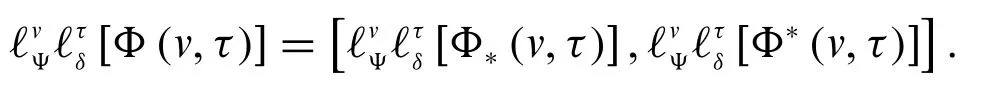
Fuzzy conformable double Laplace transform is linear.i.e.,for constantsαandβand fuzzyvalued functionsΦ(v,τ)andψ(v,τ),we have

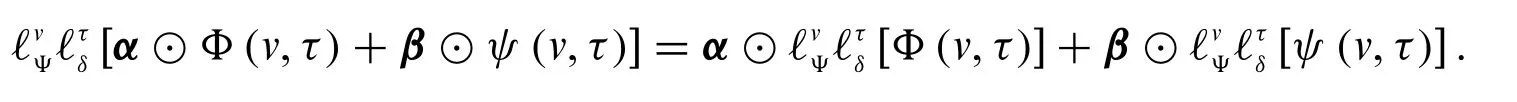
Definition 3.6.Fuzzy conformable inverse double Laplace transform is defined as

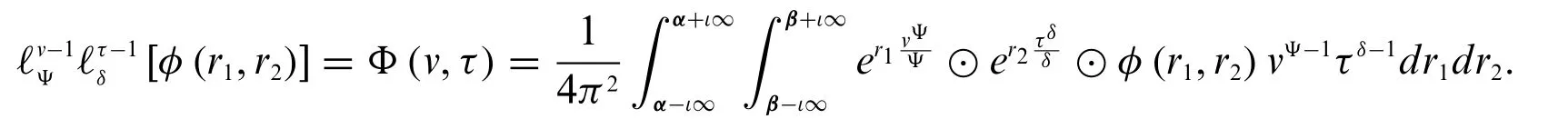
Although the fuzzy conformable double Laplace transform exists for a large variety of fuzzyvalued functions,it does not always exist.For example,fuzzy conformable double Laplace fordoes not exist because the integral does not converge.

Here we give the criteria for the existence of fuzzy conformable double Laplace transform.

Definition 3.7.A fuzzy-valued functionΦ(v,τ)is of exponential order,if for some real constantsα,β,we obtain supv,τ＞0|Φ(v,τ)|≤

Theorem 3.9.LetΦ(v,τ)be of exponential order and continuous on the interval[0,∞),then the fuzzy conformable double Laplace transform ofΦexists.

Proof.SinceΦis of exponential order,so we have

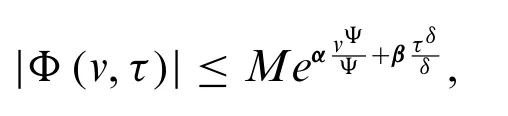
Now,we have

Now,after performing fuzzy conformable integration and taking limr1→∞,.r2→∞,we have

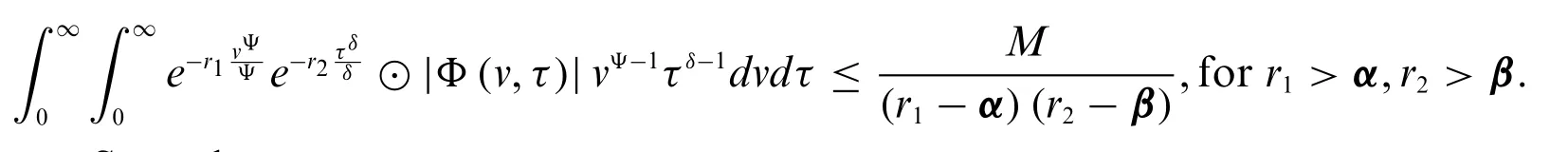
So we have

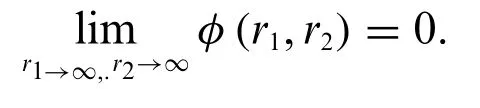
Thus proved.

Relation between fuzzy double Laplace transform and fuzzy conformable double Laplace transform is

Lemma 3.1.

Proof.From Definition 3.5,we have

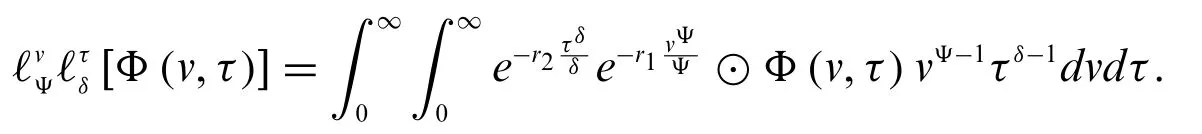
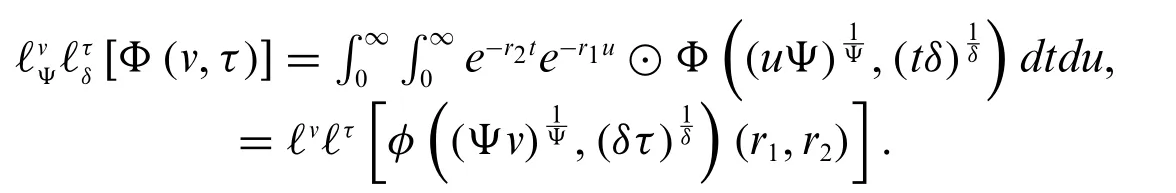
Theorem 3.10.Fuzzy conformable double Laplace transform,when applied to a strongly generalized conformable partial differentiable functionΦ(v,τ),we have four cases.

Case 1:With respect tov,we have two cases,which are

1.WhenΦis differentiable of the type(Ψ-1),then

2.IfΦis differentiable of the type(Ψ-2),then

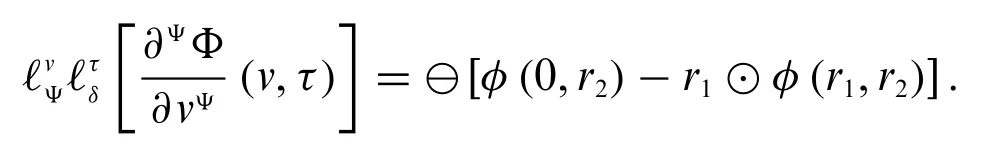
Case 2:With respect toτ,we have two cases,which are

1.IfΦis differentiable of type(δ-1),then

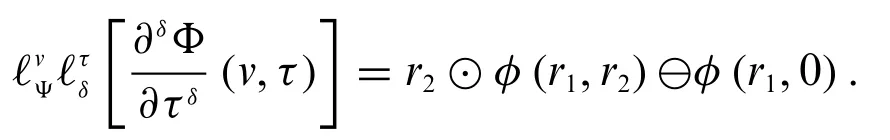
2.IfΦis differentiable of type(δ-2),then

Theorem 3.11.When we apply fuzzy conformable double Laplace on a fuzzy-valued function,which is a strongly generalized conformable partial differentiable,we have two cases.

Case 1:When we apply fuzzy conformable double Laplace transform on a strongly generalized conformable partial differentiable of order 2Ψwith respect tov,we have four cases,which are

1.If bothΦandare differentiable of type(Ψ-1),then we have

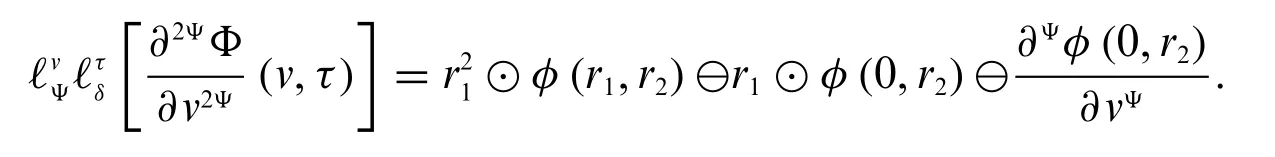
2.IfΦis differentiable of type(Ψ-1)andis differentiable of type(Ψ-2),then

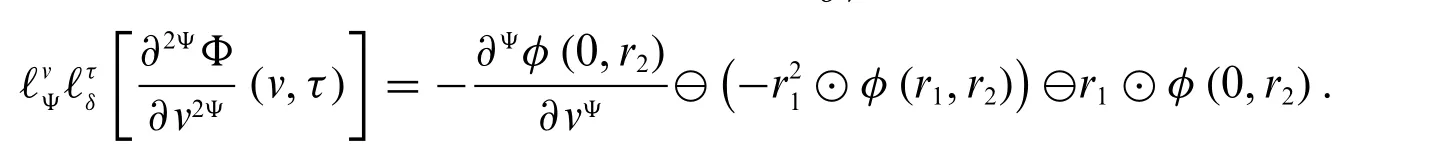
3.IfΦis differentiable of type(Ψ-2)andis differentiable of type(Ψ-1),then

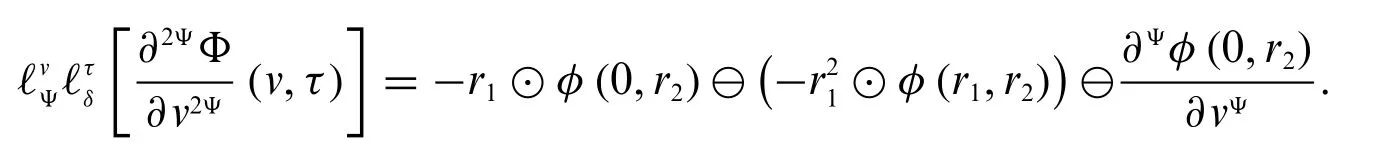
4.If bothΦandare differentiable of type(Ψ-2),then we have

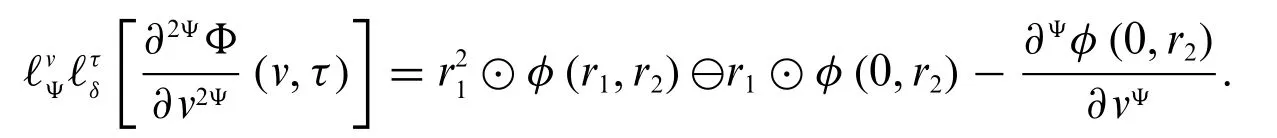
Case 2:When we apply fuzzy conformable double Laplace transform on a strongly generalized conformable partial differentiable of order 2Ψwith respect tov,we have four cases,which are

1.When bothΦandare differentiable of type(δ-1),we have

2.IfΦis differentiable of type(δ-1)andis differentiable of type(δ-2),then

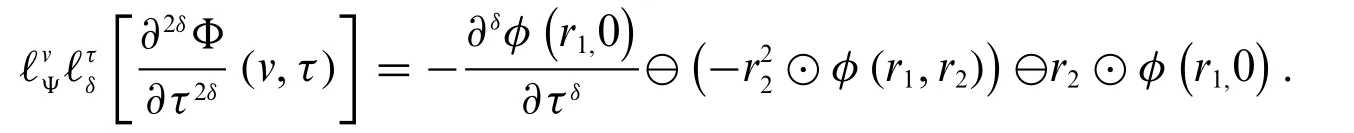
3.IfΦis differentiable of type(δ-2)andis differentiable of type(δ-1),then

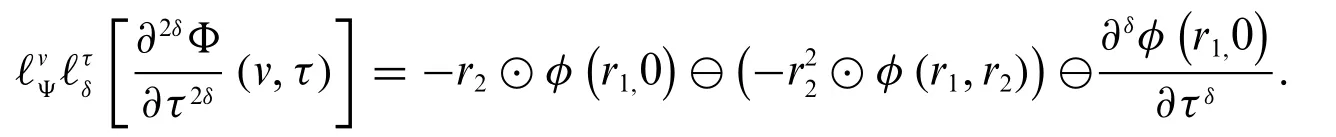
4.If bothΦandare differentiable of type(δ-2),then we have

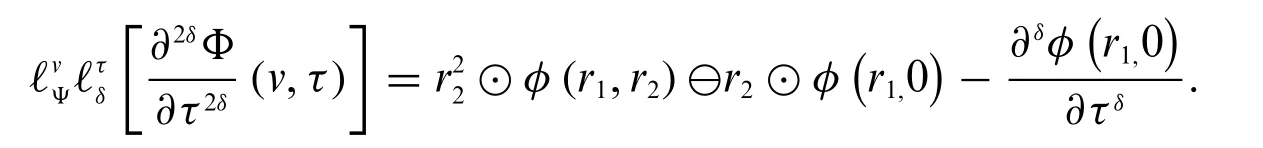
Theorem 3.12.For a fuzzy-valued function,whose fuzzy conformable double Laplace transform exists,the first translation theorem in the fuzzy conformable sense has the form

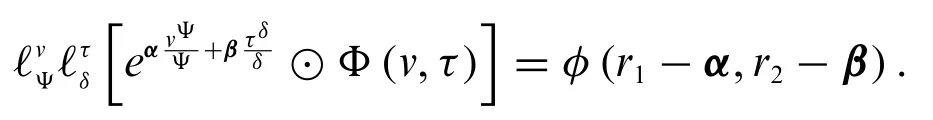
Theorem 3.13.For a fuzzy-valued function,whose fuzzy conformable double Laplace transform exists,the second translation theorem in the fuzzy conformable sense has the form

whereU(v,τ)is the Heaviside unit step function defined by

U(v-η,τ-μ)=1,whenv＞η,andτ＞μ,

U(v-η,τ-μ)=0,whenv ＜ηandτ ＜μ.

Now,we define convolution in fuzzy conformable sense and then we will state the convolution theorem.

Definition 3.8.For a fuzzy-valued functionΦand a real-valued functionψ,convolution in the fuzzy conformable sense is defined as

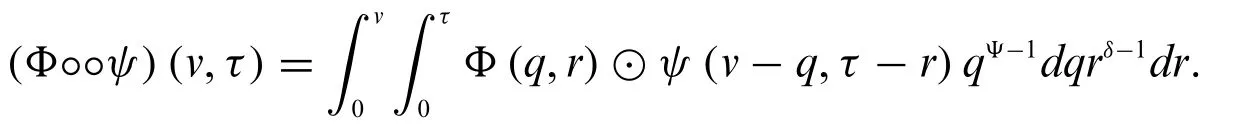
Remark 3.2.If we substitutew=v-q,u=τ-rin the above Definition 3.8,we obtain the form

Thus the fuzzy conformable convolution possesses the commutative property.

Theorem 3.14.Convolution theorem in the fuzzy conformable sense is given by

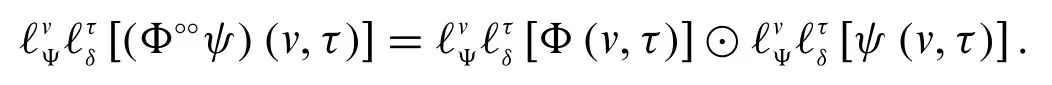
4 Fuzzy Conformable PDEs

4.1 Of Order Ψ

First,we solve fuzzy conformable partial differential equations of orderΨwhich have the general form given by

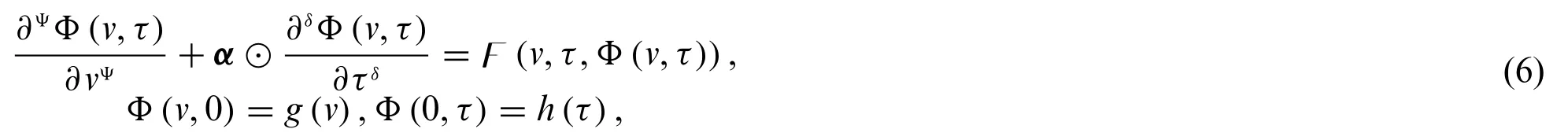
whereα∈R,Φ(v,τ)is fuzzy-valued function,h(τ)andg(v)are fuzzy numbers and F is a fuzzyvalued function which is linear with respect toΦ(v,τ).

To solve Eq.(6)with fuzzy conformable double Laplace transform,the procedure is as follows:

First,take fuzzy conformable double Laplace transforms on both sides of the Eq.(6),we obtain

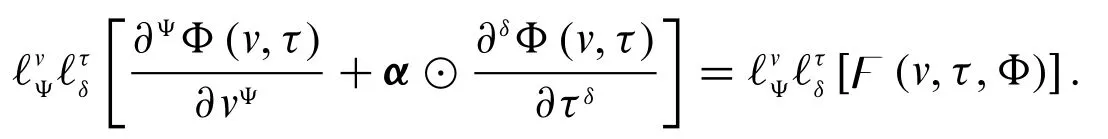
Now,we have the following four cases.

Case 1:IfΦis differentiable of type(δ-1)with respect toτand differentiable of type(Ψ-1)both

with respect tov,then

It implies that

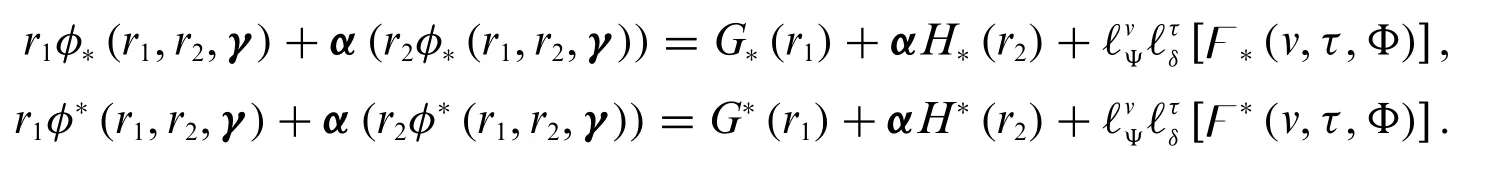
Case 2:IfΦis differentiable of type(Ψ-2)with respect tovand differentiable of type(δ-1)with respect toτ,then

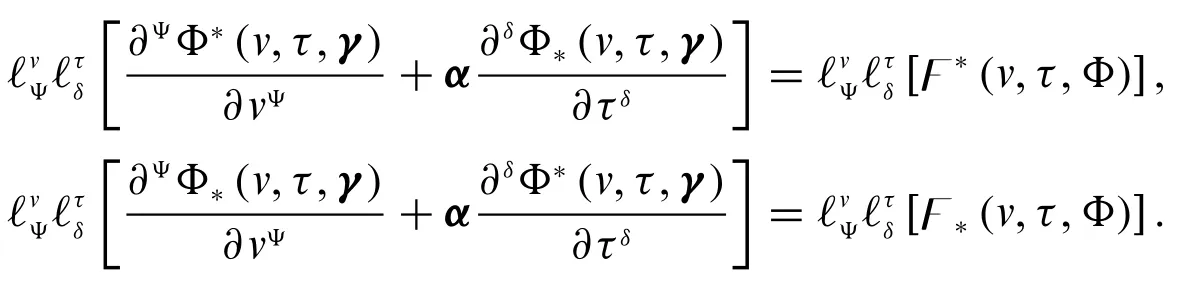
It implies that

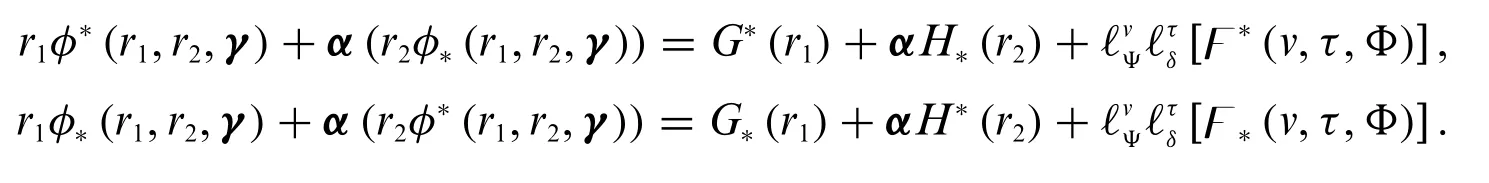
Case 3:IfΦis differentiable of type(δ-2)with respect toτand differentiable of type(Ψ-1)with respect tov,then

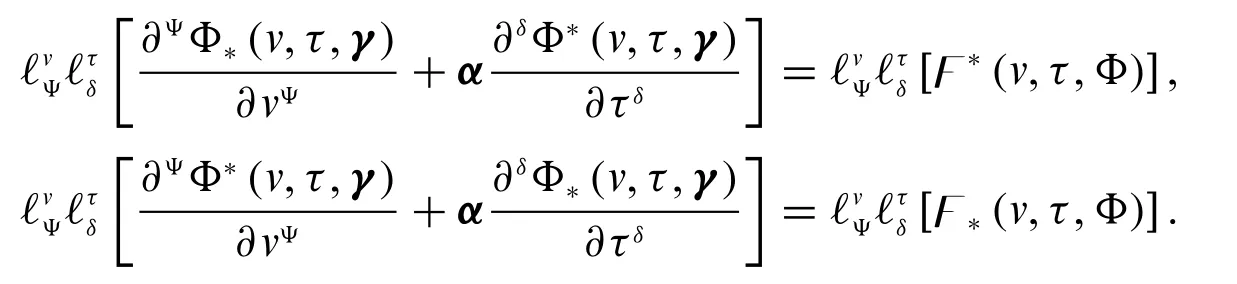
It implies that

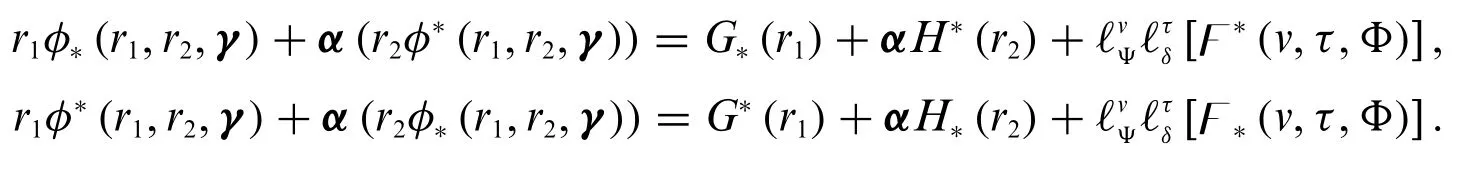
Case 4:IfΦis differentiable of type(Ψ-2)both with respect tovandτ,then

It implies that

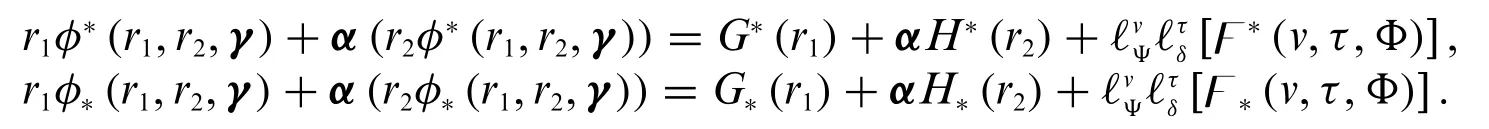
Solving the above system of equations and taking fuzzy conformable double Laplace inverse,we obtain the solution in the formΦ(v,τ,γ)=[Φ*(v,τ,γ),Φ*(v,τ,γ)].

Now,we present an example to demonstrate the feasibility of our method.

Example 4.1.Consider the fuzzy conformable partial differential equation of orderΨ

Applying fuzzy conformable double Laplace transform,we have the four cases.

Case 1:IfΦis differentiable of type(δ-1)with respect toτand differentiable of type(Ψ-1)both with respect tov,then

r2⊙φ(r1,r2)⊖φ(r1,0)=r1⊙φ(r1,r2)⊖φ(0,r2).

Now,we have

r2φ*(r1,r2,γ)-φ*(r1,0,γ)=r1φ*(r1,r2,γ)-φ*(0,r2,γ),

r2φ*(r1,r2,γ)-φ*(r1,0,γ)=r1φ*(r1,r2,γ)-φ*(0,r2,γ).

Now,after solving and using boundary and initial condition,we have

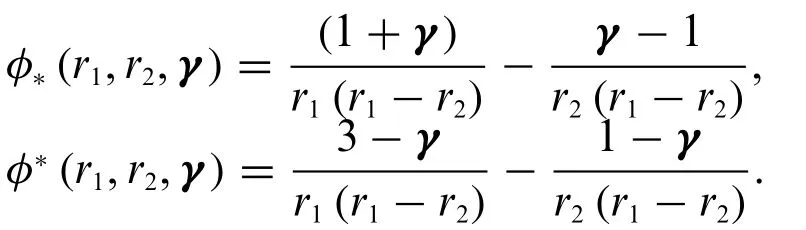
Case 2:IfΦis differentiable of type(δ-1)with respect toτand differentiable of type(Ψ-2)with respect tov,then

-φ(r1,0)⊖(-r2⊙φ(r1,r2))=-φ(0,r2)⊖(-r1⊙φ(r1,r2)).

Now,we have Now

r2φ*(r1,r2,γ)-φ*(r1,0,γ)=r1φ*(r1,r2,γ)-φ*(0,r2,γ),

r2φ*(r1,r2,γ)-φ*(r1,0,γ)=r1φ*(r1,r2,γ)-φ*(0,r2,γ).

After solving and using boundary and initial condition,we have

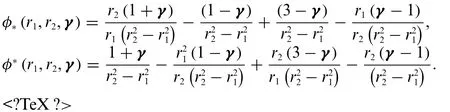
Case 3:WhenΦ(v,τ)is differentiable of type(Ψ-1)with respect tovand differentiable of type(δ-2)with respect toτ,we have-φ(r1,0)⊖(-r2⊙φ(r1,r2))=r1⊙φ(r1,r2)⊖φ(0,r2).

Now,we have

r2φ*(r1,r2,γ)-φ*(r1,0,γ)=r1φ*(r1,r2,γ)-φ*(0,r2,γ),

r2φ*(r1,r2,γ)-φ*(r1,0,γ)=r1φ*(r1,r2,γ)-φ*(0,r2,γ).

Now,after solving and using boundary and initial condition,we have

Case 4:WhenΦ(v,τ)is differentiable of type(Ψ-2)with respect tovand differentiable of type(δ-2)with respect toτ,we have

-φ(r1,0)⊖(-r2⊙φ(r1,r2))=-φ(0,r2)⊖(-r1⊙φ(r1,r2)).

Now,we have

r2φ*(r1,r2,γ)-φ*(r1,0,γ)=r1φ*(r1,r2,γ)-φ*(0,r2,γ),

r2φ*(r1,r2,γ)-φ*(r1,0,γ)=r1φ*(r1,r2,γ)-φ*(0,r2,γ).

Now,after solving the above system of equations and using boundary and initial condition,we have

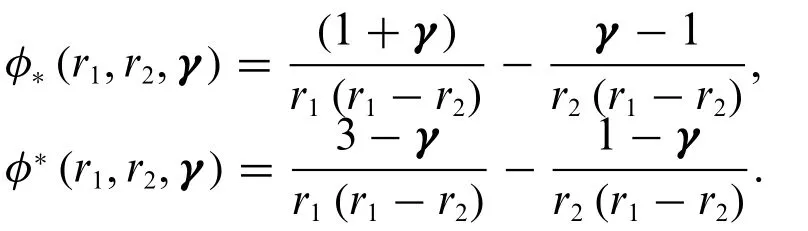
Now solving the above systems of equations,and applying the fuzzy conformable double Laplace inverse,we get the solution.

Example 4.2.Consider the following fuzzy conformable partial differential equation:

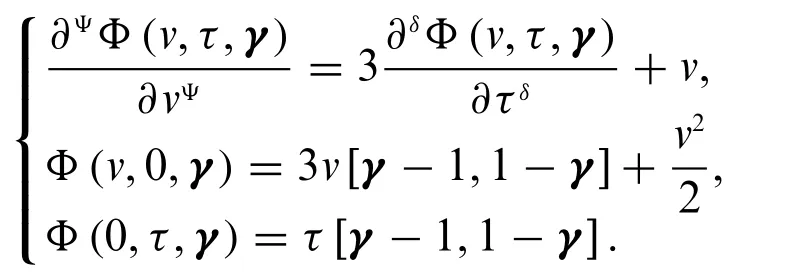
We have the four cases.

Case 1:IfΦis differentiable of type(δ-1)with respect toτand differentiable of type(Ψ-1)with respect tov.

Case 2:IfΦis differentiable of type(δ-1)with respect toτand differentiable of type(Ψ-2)with respect tov.

Case 3:IfΦis differentiable of type(Ψ-1)with respect tovand differentiable of type(δ-2)with respect toτ.

Case 4:IfΦis differentiable of type(Ψ-2)with respect tovand differentiable of type(δ-2)with respect toτ.

From fuzzy conformable double Laplace transform,we can get the analytical solutions for all the above cases,as discuss in last example.Here,we consider the graphical representation of case 1,rest are the same.Forδ=Ψ=1,we obtain

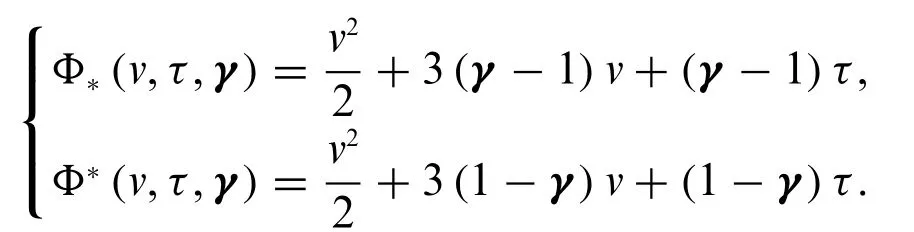
ThenΦ(v,τ,γ)=[Φ*(v,τ,γ),Φ*(v,τ,γ)]for all 0 ≤γ≤1.Forγ=0,we have the following:

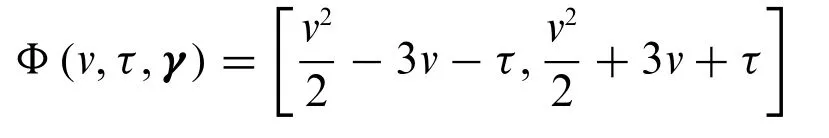
and its graph is given in Fig.1.

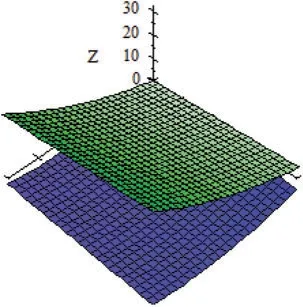
Figure 1:Graph of Φ(v,τ,γ)=[Φ*(v,τ,γ),Φ*(v,τ,γ)]with γ=0

Forγ=0.5,we have the following:

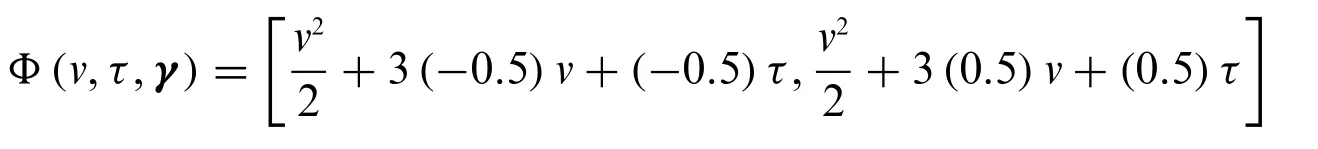
and its graph is given in Fig.2.

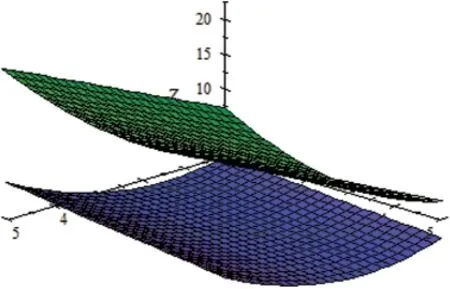
Figure 2:Graph of Φ(v,τ,γ)=[Φ*(v,τ,γ),Φ*(v,τ,γ)]with γ=0.5

Forγ=0.7,we have the following

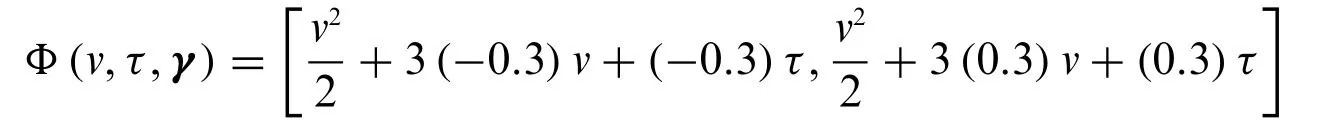
and its graph is given in Fig.3.

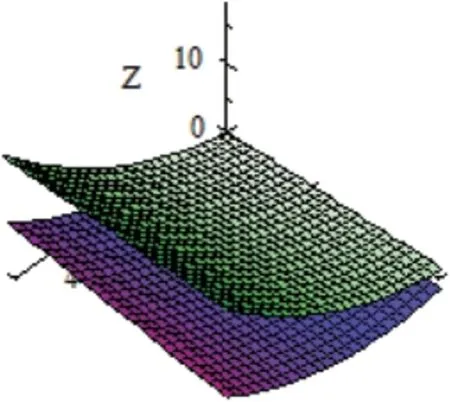
Figure 3:Graph of Φ(v,τ,γ)=[Φ*(v,τ,γ),Φ*(v,τ,γ)]with γ=0.7

Forγ=1,we have the following:

and its graph is given in Fig.4.

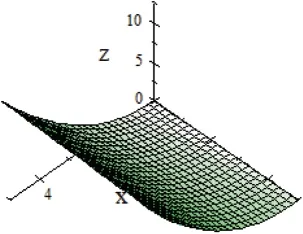
Figure 4:Graph of Φ(v,τ,γ)=[Φ*(v,τ,γ),Φ*(v,τ,γ)]with γ=1

4.2 Of Order 2Ψ

In this subsection,we solve fuzzy conformable heat equation and fuzzy conformable wave equation using fuzzy conformable double Laplace transform.

4.2.1 Heat Equation

Fuzzy conformable heat equation in one dimension has many forms such as

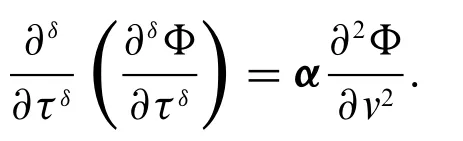
Also,this form has been used by some researchers

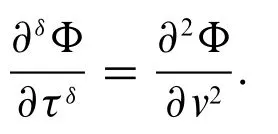
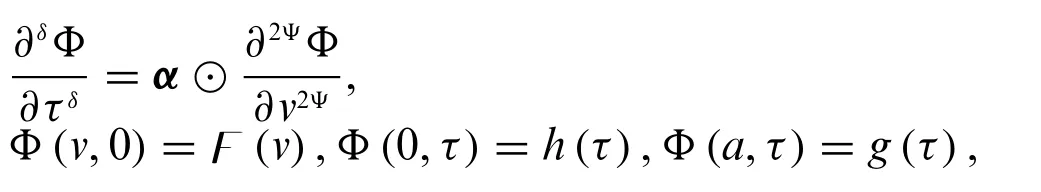
We use the fuzzy conformable heat equation in the form whereΦis a temperature of a rod of a constant-cross section and homogeneous material,lying along the axis,andαis a constant of diffusion.We have taken initial and boundary conditions as fuzzy numbers.For simplicity,we takeα=1.

To solve fuzzy conformable heat equation with fuzzy conformable double Laplace transform,the procedure is as follows:

First,apply fuzzy conformable double Laplace transform on both sides of the fuzzy conformable heat equation.

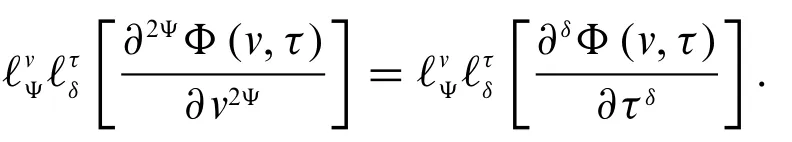
The fuzzy conformable heat equation is changed into the conformable boundary value problem.

1.WhenΦ(v,τ)is differentiable of the type(δ-1),we have four cases associated with the four

types of derivatives with respect to order 2Ψ.

2.WhenΦ(v,τ)is strongly generalized conformable partial differentiable of the type(δ-2),we again have four cases associated with the four types of derivatives with respect to order 2Ψ.

Now,solving the above systems of equations and applying boundary conditions,and then implementing fuzzy conformable double Laplace inverse transform,we get the solution in the formΦ(v,τ,γ)=[Φ*(v,τ,γ),Φ*(v,τ,γ)].

Now,we interpret the benefits of our method with an example.

Example 4.3.Consider fuzzy conformable heat equation

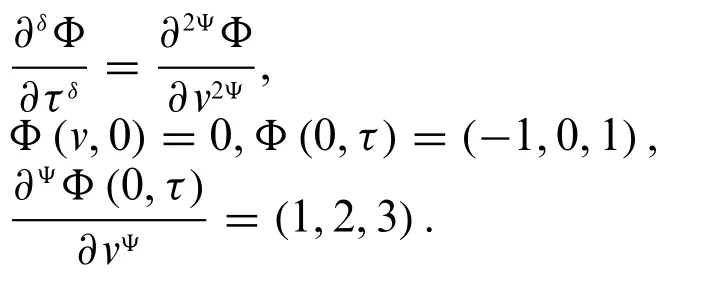
Fuzzy conformable double Laplace transform implies eight cases of the above system.Here,we consider four nontrivial cases for the solution.

Fuzzy conformable double Laplace inverse can yield the required solutions.

4.2.2 Wave Equation

Let us consider the following 1D fuzzy conformable wave equation

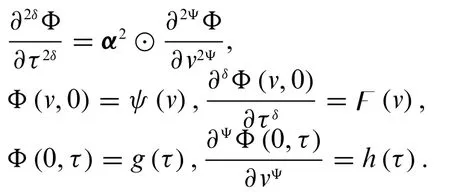
To solve the fuzzy conformable wave equation with the fuzzy conformable double Laplace transform,the procedure is as follows:

First,apply fuzzy conformable double Laplace transform on both sides of the fuzzy conformable wave equation.As a result,we have possible sixteen cases.

1.First,we takeΦ(v,τ)andas differentiable of the type (Ψ-1) with respect tov.It implies four associated cases.

2.Now,we takeΦ(v,τ)andas differentiable of the type(Ψ-2),then we have four associated cases.

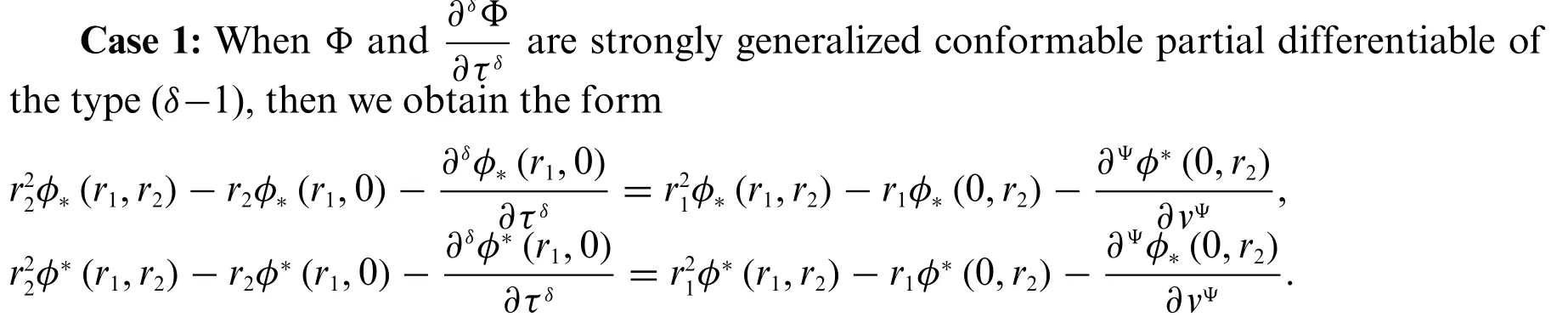
3.As a third option,we takeΦas strongly generalized conformable partial differentiable of the type(Ψ-2)andas strongly generalized conformable partial differentiable of the type(Ψ-1),which enables us to have four cases associated with the four types of derivative forτ,which are given by

4.In the fourth case,we takeΦas strongly generalized conformable partial differentiable of the type(Ψ-1)andas strongly generalized conformable partial differentiable of the type(Ψ-2),which enables us to have four cases associated with the four types of derivative forτ,which are given by

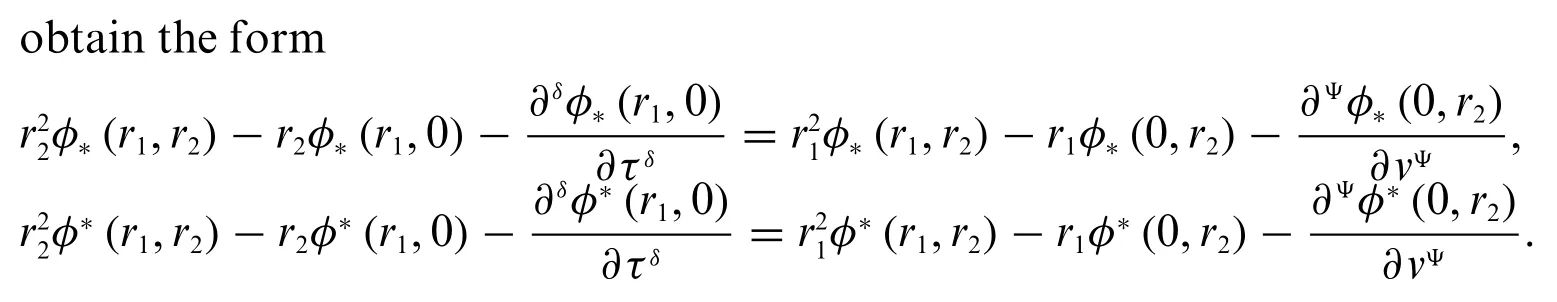
Solving the above systems of equations,and apply the fuzzy conformable double Laplace inverse,we can get the solution in the formΦ(v,τ,γ)=[Φ*(v,τ,γ),Φ*(v,τ,γ)].

Now,we present an example of the fuzzy conformable wave equation to demonstrate the validity of our results.

Example 4.4.Consider fuzzy conformable wave equation in one dimension is

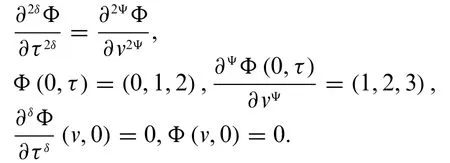
Fuzzy conformable double Laplace transform implies sixteen possibilities.We consider here only nontrivial four cases for the solution.

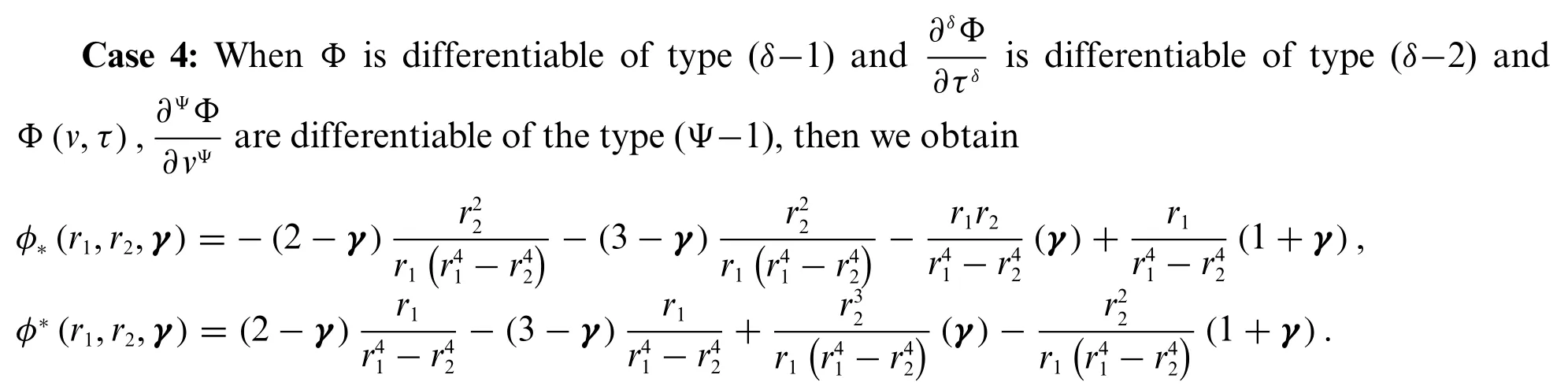
After solving the above system,and applying the fuzzy conformable double Laplace inverse,we can get the required solution.

5 Conclusion

We have introduced the fuzzy double Laplace transform and fuzzy conformable double Laplace transform.Also,related properties and theorems for derivatives and integrals of the transform are presented.We apply the fuzzy conformable double Laplace transform in this manuscript to obtain the solutions of fuzzy conformable PDEs (both in 1D and 2D).The fuzzy conformable PDEs are solved using this approach without transforming into conformable partial differential equations,so it is not important to find a solution to the partial differential equation.This is the greatest benefit of this system.The double Laplace transformation technique,therefore,is very convenient and effective.However,explicit solutions for each system require inverse double Laplace transform,which is complicated to solve.In future work,we will obtain numerical solution methods to overcome these complications.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: The author Manar A.Alqudah would like to thank Princess Nourah bint Abdulrahman University Researchers Supporting Project No.(PNURSP2022R14),Princess Nourah bint Abdulrahman University,Riyadh,Saudi Arabia.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.