衰减信道下具有严格时延的P2P实时通信传输策略

田世坤,唐胜达

(广西师范大学 数学与统计学院，广西 桂林 541006)

无线网络发展的主要方向是宽带数据通信和数据实时交互，互联网和蜂窝通信的增加，对高速通信链接的需求也日益增多[1-2]。网络信息时代的高速发展，导致网络信息种类越来越来复杂，网络安全性挑战亦不容乐观[3]。数据交互的爆炸式增长为基站的宏观调控带来巨大挑战。为解决通信调度相关问题，学者们做了很多努力，相关可用技术包括数字用户线路转换(DSL)[4]、点对点(P2P)无线通信[5-6]、电缆混合系统[7-8]以及卫星链路[9-10]等。由于低成本、易实现、高安全性，P2P通信已变得越来越普及。

P2P无线通信使得网络上的沟通、共享和交互变得更容易、更直接。在P2P无线通信中，利用信道状态信息(CSI)对网络进行跨层优化，并提高信道利用率是无线通信优化的一个重要问题。近年来，电信工程中基于P2P无线通信网络的研究有很大发展,例如，针对长距离P2P链路，文献[11]提出一种满足远程点对点密集波分多路复用(DWDM)链路需求的网络设计方法，降低P2P无线通信的错误率和Q-Factor；在技术应用上，文献[12]提出一种基于CSI的物联网设备的身份认证机制，在衰落信道下考虑数据的实时传输；文献[13]研究在CSI无法观测时的P2P无线传输问题，将调度模型建模为部分可观测的MDP(POMDP)进行研究；文献[14]考虑D2D通信调度问题，研究在随机数据包到达、数据包丢失和异构截止日期等制约下的实时通信策略；基于有限状态的Markov信道模型及ARQ重传协议,文献[15]考虑数据包从用户到基站的实时传输策略，给出了传输策略的阈值结构。

本文提出衰减信道下P2P实时通信模型，与上述文献相比，本文的主要贡献如下：1)提出P2P实时通信模型，具体地，在系统模型中加入CSI，弥补了文献[14]对于CSI相关影响的忽略。考虑CSI对于P2P实时通信系统的影响，将无线传输系统建模为一个有限状态的Markov决策过程(FSMDP)。2)引入拉格朗日数乘因子，基于RBP理论证明无线调度问题的可索引性，为设计衰减信道下P2P基于Whittle索引的实时传输策略提供理论支持。3)基于衰减信道下P2P实时通信系统，给出P2P的实时通信Whittle索引传输策略的封闭表达式，推广了文献[15]最优传输调度策略阈值结构的阈值表达式。

本文其余部分结构如下：第1章描述实时P2P通信模型；第2章构建调度问题的MDP模型；第3章证明P2P实时通信系统的可索引性，并给出Whittle索引封闭解；第4章给出算法分析以及仿真结果；第5章是结语。

1 模型和问题

本文主要考虑衰落信道下P2P实时通信的传输调度问题,下面给出P2P实时通信模型。

1.1 模型

考虑离散时间的通信系统，将时间划分为大小相等的时隙，将时隙集合记为H={0，1，2，…}。由于阴影、多路径传播、多用户干扰和移动性等影响，无线通信信道通常是相关衰落的，类似文献[16-19]，设衰减信道模型为X={Xt,t∈H}，将衰减信道状态分为M个不重叠区间，每个区间都映射为一个信道状态，记信道状态空间为Γ={γ1,γ2,…,γM}，其中M<+∞。假设每个时隙间信道状态不发生改变，不同时隙间信道状态可以发生变化。设信道状态转移概率矩阵为Pc=[pc(γn|γm)]M×M，其中，pc(γn|γm)表示信道状态从γm转移到γn的概率，即

pc(γn|γm)=P(Xt+1=γn|Xt=γm),γm,γn∈Γ。

称X为Markov衰减信道模型,其中，转移概率矩阵可通过观测拟合得到。

本文考虑P2P实时通信，系统将需要传输的数据存储在缓存器中，由发射器在严格时延要求下发送给接收端。在最大容忍时延内，发射器必须完成数据传输，否则将强制结束该数据传输任务，即丢包。设发射端的传输任务(数据)大小为L，最大容忍时延为N, 即发射端需要在N个时隙内完成L个数据包的传输，超过时延的数据包因延时而被丢失。本文假定传输任务中的数据包大小给定，且每个时隙内至多只能发射一个数据包。

如图1所示，在每个时隙内，系统根据当前状态确定是否传输数据包，当系统决定传输数据包时，发射端则将数据包发送给用户。数据包传输受信道状态影响，设p(γm)表示信道状态为γm时数据包传输成功的概率，若传输失败，数据包可允许重传。当N个传输时隙结束时，仍在缓冲区中等待传输的数据包被丢弃，同时，新的传输任务以一定概率到达发射端并开始传输。设Q为新的传输任务到达发射端的概率，不失一般性，设每个到达的传输任务都具有相同的大小和时延。

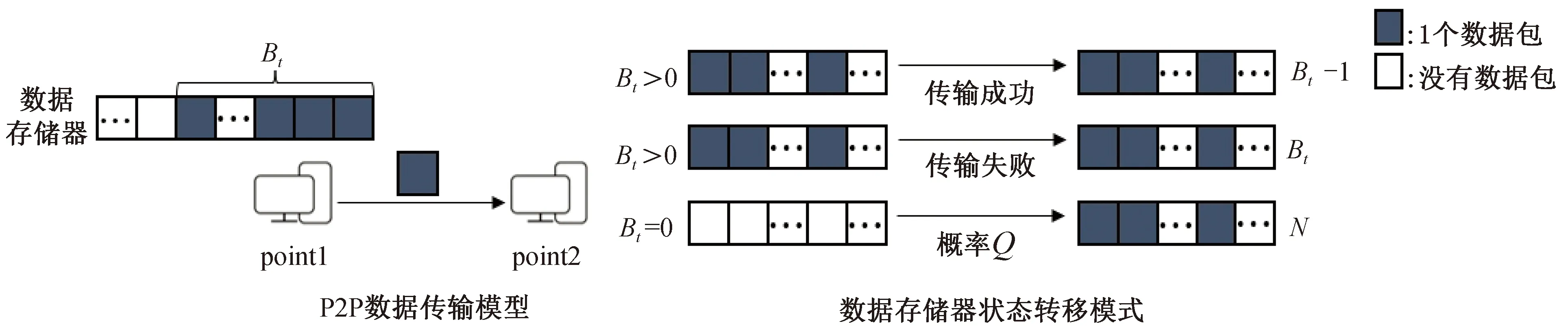
图1 P2P传输模型Fig. 1 P2P transmission model

在时刻t，记当前正在传输的任务中剩余数据包个数为Bt∈{0,1,…,L}，剩余传输时间为Tt∈{0,1,…,N}，记st=(Xt,Tt,Bt)为系统t时刻的状态，称为衰减信道下传输任务随机到达的实时P2P通信模型，st为系统在t∈H时刻的状态。本文P2P通信模型是对文献[14]中模型的推广。

S={st,t∈H}

(1)

1.2 问题描述

设at表示在时刻t系统采取的动作，具体地，at=1表示在时刻t发射器传输数据包，at=0表示在时刻t发射器不传输数据包。记A={0,1}，称A为系统的动作空间。设每个数据包传输成功时系统可获得收益r>0，否则收益为0。设时刻t信道状态为Xt=γm时的传输成本为c(γm)。对P2P通信模型(1)，设g={at(st)|at(st)∈A,st∈S,t∈H}为系统采取的传输策略，用R(st,at)表示在时刻t系统获得的收益，则系统在策略g下的贴现总期望收益为

Vg(st)=

(2)

式中：β∈(0,1)表示贴现因子；[·|st]表示初始状态为st时的条件期望。

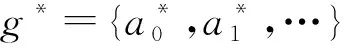
(3a)

BtI{Tt-=0}=0，

(3b)

则称g*为系统的最优传输策略，其中，I{·}表示示性函数。约束条件(3b)表示在传输时间截止时刻，传输任务中未传数据包个数为0，即在传输截止时刻，系统需完成所有数据包的传输。

本文主要目标是求最优传输策略g*，使得系统在满足时延约束条件(3b)下，贴现总期望收益(2)最大。

2 调度问题的MDP框架

本章将P2P通信的传输调度问题在MDP构架内重构，同时基于MDP理论给出相应最优传输策略和最大贴现总期望收益算法。

为了在MDP框架下讨论P2P通信问题，首先要将带约束条件(3b)的传输调度问题转换成无约束条件的Markov决策问题。本文采用文献[20]的思想，引入惩罚函数，当任务在给定传输时间内完成时，设惩罚函数为0，而当任务没有在设定的时限内完成时，则系统会得到一个很大惩罚(负收益)。为了获得最大收益，系统将规避那些无法在给定时间内完成传输任务的传输策略，从而保证时延约束条件(3b) 成立。基于这一思想，本文分别从状态空间、动作空间、转移概率及收益函数来重构MDP。

① 状态空间： S={st=(Xt,Tt,Bt),t∈H}。

② 动作空间： A={0,1}。

③ 转移概率： 记P(st+1|st,at)表示采用动作at时，系统状态从st转移到st+1的概率。设当前系统状态st=(Xt,Tt,Bt)，其中Xt=γm。考虑如下3种情形：

a)当动作at=1，Tt>1时，设Xt+1=γn,∀γn∈Γ，系统状态转移到st+1=(Xt+1,Tt-1,(Bt-at)+)的概率为pc(γn|γm)p(γm)，即数据包传输成功的概率，其中，(x)+=max{0,x}；系统状态转移到st+1=(Xt+1,Tt-1,Bt)的概率为pc(γn|γm)(1-p(γm))，即数据包传输不成功的概率。

b)当动作at=0，Tt>1时，则状态以概率pc(γn|γm)转移到st+1=(Xt+1,Tt-1,Bt)。

c)当Tt<1时，数据包不论传输是否完成都会被丢包，即系统以概率Q进入状态(N,L)，以(1-Q)进入状态(0,0)。

④ 收益函数：引入惩罚函数f(b)，其中b为截止时刻剩余数据包的个数，当b=0时，令f(0)=0，当b≠0时，令f(b)是b的递增凹函数，即剩余数据包越多，产生的惩罚越大，则系统收益Rt(st,at)为

于是，具有约束条件的P2P 通信调度问题转换成了无约束条件的无限时间的贴现MDP模型。V(st)满足如下Bellman方程基于MDP理论可知式(4)存在最优平稳传输策略[21]，利用策略迭代(PI)、值迭代(VI)等算法可求解最优策略及最大期望总收益。

(4)

本文研究的P2P实时无线传输模型的状态空间为|S|=|Γ||N||L|，传输任务的增大，或传输任务最大容忍时延的增大，将导致系统状态空间呈指数增长，从而导致求解过程中需要极大计算力和计算时间，这意味着MDP模型遭受了维数灾难。显然在状态空间很大的模型中，值迭代或策略迭代算法的计算难度很大，求解最优策略的成本高。

针对上述问题，本文引入拉格朗日数乘因子，将MDP模型转化为RBP模型，并证明RBP模型的可索引性，进而得出P2P实时通信系统的Whittle索引的封闭表达式，并给出一种时间复杂度低的基于Whittle索引的调度算法。基于Whittle索引的调度算法可以在极少计算成本下得到P2P实时通信系统的调度策略。

3 调度问题的RBP框架

本章基于RBP框架求解近似最优传输策略。

3.1 基于Whittle索引的RBP框架

记Rw(st,at)=R(st,at)+wI{at=0}，称Rw为w-补贴收益函数，w为引入的拉格朗日数乘因子，可理解为采取动作0时系统得到的额外补贴。

基于w-补贴收益的最大贴现总期望收益函数Vw(st)可表示为

(5)

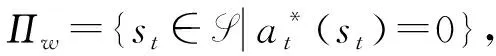
为方便表述，给定st∈S ，记

定义2[23]给定状态st∈S ，记w*(st)=inf{w|J0(st)≥J1(st)},称w*(st)是状态st的Whittle索引。

定义3[23]若Πw关于w递增，即对于任意w1、w2∈R，当w1≤w2时，有Πw1⊆Πw2，则称P2P实时通信系统具有可索引性。

3.2 基于Whittle索引的调度策略

对任意st=(xt,Tt,Bt)∈S ，令

J(st)=J0(st)-J1(st)。

(6)

显然，当w=-∞时，J(st)=J(xt,Tt,Bt)=-∞；当w=+∞时，J(st)=+∞。注意到J(st)关于w的连续性，则存在w，使得J(st)=0。因此，证明状态st的Whittle索引唯一存在性，即证方程(6)零解的唯一存在性。

类似文献[15]中定理1和定理2的证明，可得如下引理1。引理1描述了w*(st)的单调性。

引理1若状态st=(Xt,Tt,Bt)∈S ，其中，Xt=γm∈Γ，存在Whittle索引w*(st)，则

①w*(st)关于Tt非增；

②w*(st)关于Bt非减。

引理2给定状态st=(Xt,Tt,Bt)∈S ，其中，Xt=γm∈Γ，则

① 当Tt=0时，状态st的Whittle索引存在；

② 当Tt≠0,Bt=0时，状态st的Whittle索引存在；

③ 当Tt=1时，状态st的Whittle索引存在。

证明先证明①。当Tt=0时，必有Bt=0时， 此时

Vw(Xt,0,0)=max{w+βUw,-c(γm)+βUw}，

式中Uw=[QVw(Xt+1,N,L)+(1-Q)Vw(Xt+1,0,0)]。故J(Xt,0,0)=w+c(γm)，从而

w*(Xt,0,0)=-c(γm)。

(7)

再证明②。当st=(Xt,k,0)时，类似①的证明，有

w*(Xt,k,0)=-c(γm)。

(8)

最后证明③。当Tt=1时，分如下2种情况讨论：

a)当Bt=0时，同①可得

w*(Xt,1,0)=-c(γm)。

(9)

b)当Bt≠0时，有J(Xt,1,Bt)=w-rp(γm)+c(γm)+p(γm)f(Bt-1)-p(γm)f(Bt),从而

w*(Xt,1,Bt)=rp(γm)-c(γm)-p(γm)f(Bt-1)+p(γm)f(Bt)。

(10)

于是Tt=1时命题得证。综上，引理得证。

引理3若状态st=(Xt,Tt,Bt)∈S ，Xt=γm∈Γ存在Whittle索引w*(st)，其中，Tt≥2，令

g(st)=Vw(Xt,Tt,Bt+1)-Vw(Xt,Tt,Bt),

则

(11)

证明当Bt=0时，由引理2，命题显然成立。

当Bt≥1时，有

J(Xt,Tt,Bt)=w-rp(γm)+c(γm)+βp(γm)[g(Xt+1,Tt-1,Bt-1)]。

对J(xt,Tt,Bt)关于w求导，有

又因(Xt,Tt,Bt)存在Whittle索引，故引理得证。

下面给出本文的第1个主要结论(定理1)。

定理1基于RBP框架的P2P传输问题存在Whittle索引。

证明本定理即证任意给定状态st=(Xt,Tt,Bt)∈S ，Xt=γm∈Γ，存在Whittle索引w*(st)。下面用数学归纳法证明。

由引理2知，当Tt=0，1时，命题成立。

假设Tt=k时命题成立，由引理3，有

(12)

下面证明当Tt=k+1时，w*(st)存在。

当Bt=0时，由J(Xt,k+1,0)=w+c(γm)，可得w*(Xt,k+1,0)=-c(γm)。

当Bt≥1时，J(Xt,k+1,Bt)=w-rp(γm)+c(γm)+βp(γm)[g(Xt+1,k,Bt-1)]，由式(12)，得

故当Tt=k+1时，w*(st)存在。综上，对于任意st∈S 都存在Whittle索引。命题得证。

下面给出本文的第2个主要结论(定理2)，该结论给出各个状态Whittle索引的封闭表达式。

定理2系统状态st=(Xt,Tt,Bt)∈S 的Whittle索引可表示为

(13)

式中：

同时，对∀γn∈Γ，有ρ=[p(γn)]，ζ=[c(γn)]。

证明式(13)前2式由式(7)～(10)可得，接下来只需证明式(13)中第3式，即Tt>1,Bt≠0时状态st的Whittle索引表达式。

由引理1，当Bt=0时，有w*(Xt,Tt,1)≥w≥w*(Xt,Tt,0)=-c(γm)，

g(Xt,Tt,0)=rp(γm)-c(γm)+β(1-p(γm))[g(Xt+1,Tt-1,0)]-w。

(14)

当Bt≠0时，有w*(Xt,Tt,Bt+1)≥w≥w*(Xt,Tt,Bt)，以及

g(Xt,Tt,Bt)=rp(γm)-c(γm)+β(1-p(γm))[g(Xt+1,Tt-1,Bt)]-w。

(15)

由此可得

g(Xt,1,0)=rp(γm)-c(γm)-(1-p(γm))δ(0)-w，

(16)

g(Xt,1,Bt)=rp(γm)-c(γm)-(1-p(γm))δ(Bt)-w。

(17)

1)当Tt>1,Bt=1时

J(Xt,Tt,1)=w-rp(γm)+c(γm)+βp(γm)[g(Xt+1,Tt-1,0)]，

(18)

对∀γn,γn′,…,γnTt-3∈Γ，将式(14)代入式(18)进行Tt-1次替换可得

J(Xt,Tt,1)=w-rp(γm)+c(γm)+βp(γm)[rp(γn)-c(γn)+β(1-p(γn))[rp(γn′)-c(γn′)+…+

β(1-p(γnTt-3))[g(Xt+Tt-1,1,0)]-w]…-w]-w],

代入式(16)，并取J(xt,Tt,Bt)=0即可得到定理2。

2)当Tt>1,Bt>1时

J(Xt,Tt,Bt)=w-rp(γm)+c(γm)+βp(γm)[g(Xt+1,Tt-1,Bt-1)]。

(19)

将式(15)代入式(19)进行Tt-1次替换可得

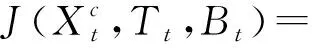
β(1-p(γnTt-3))[g(Xt+Tt-1,1,Bt-1)]-w]…-w]-w],

代入式(17)，并取J(Xt,Tt,Bt)=0即可得到定理2。命题得证。

注在P2P实时通信的MDP模型中，w=0。由定理2可计算出所有状态所对应的Whittle索引w*(st)，并由此得到基于Whittle索引的调度算法，具体地，当w*(st)>0时，采取动作at=1；否则采取动作at=0。

4 数值模拟

4.1 数值设置

设信道状态空间为Γ={1,2,3},分别表示差、一般、好3种情况，对应的成功传输概率为P=[0.45,0.7,0.85]。设信道状态具有平稳分布Pc=[0.2,0.5,0.3]。对任意信道状态γm∈Γ，令数据包的发送成本函数为：c(γm)=2/γm，贴现因子β=0.85。假设传输任务的大小为L=5，传输任务的最大容忍时延N=10。成功传输一个数据包的收益为r=3，剩余数据包对应的惩罚函数为f(b)=b2I{b≠0}。

4.2 仿真结果及分析

表1给出3个信道状态、不同剩余数据包个数下，剩余传输时间不同时对应状态所采取的动作，其中(a,b,c)这3个分量分别对应3个信道状态下的策略。由表1所给出的策略可以得到最大贴现总收益。图2为基于Whittle索引实时传输算法和基于VI算法的最大贴现总收益的对比。通过对比可以看出，在信道状态较差时，基于Whittle索引的最优调度算法的最大贴现总收益与值迭代算法(VI)相比有些不足，信道状态一般或较好的情况下与值迭代算法相等，由此可得基于Whittle索引的最优调度算法的最大贴现总收益近似于最优。通过仿真实验可得，基于Whittle索引实时传输策略的计算成本是VI算法的0.585 8。同时，由图2可见，通过Whittle索引得到的调度策略与最优调度策略几乎没有区别。

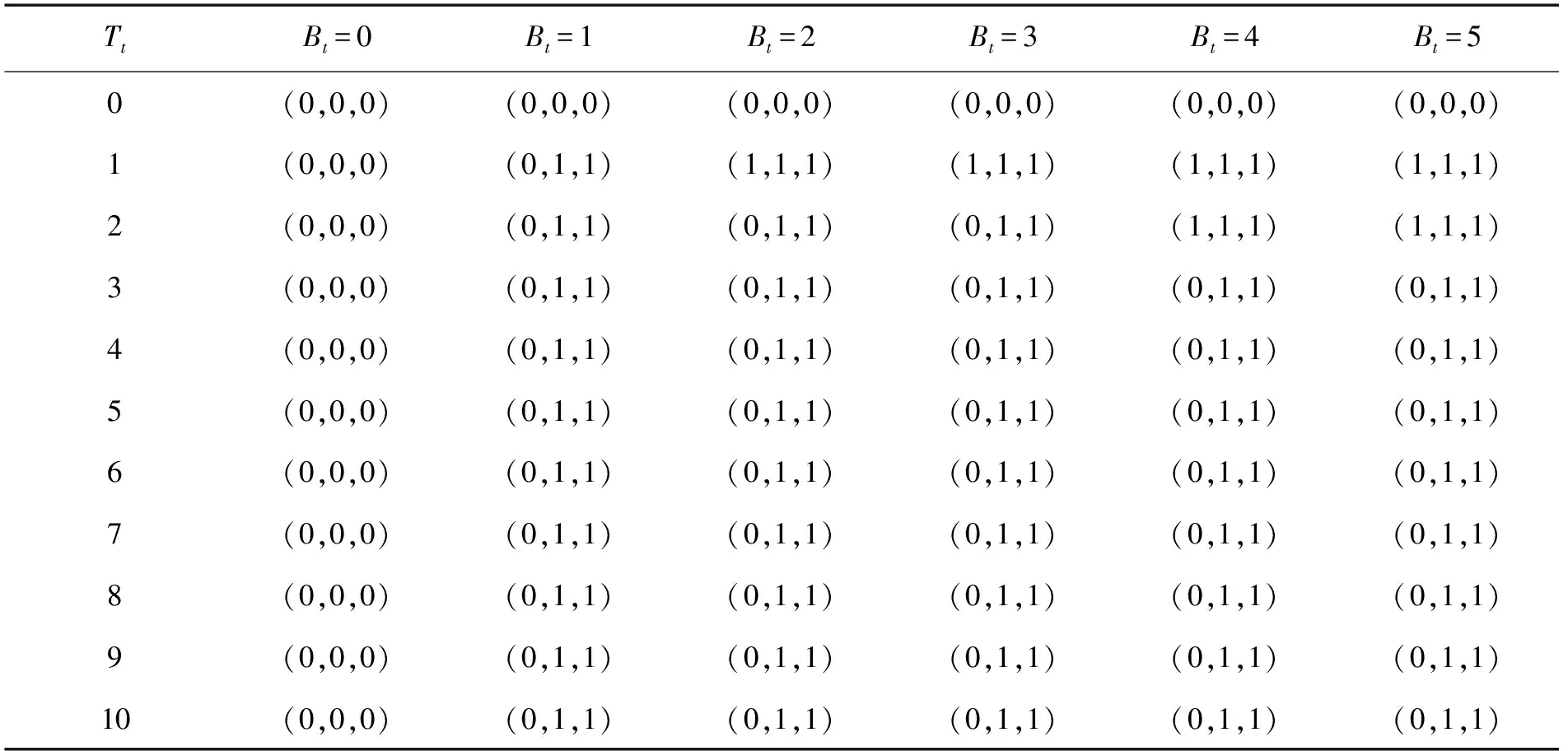
表1 基于Whittle索引的最优调度策略下所有系统状态的动作Tab. 1 Actions of all system states under the optimal scheduling policy based on Whittle index

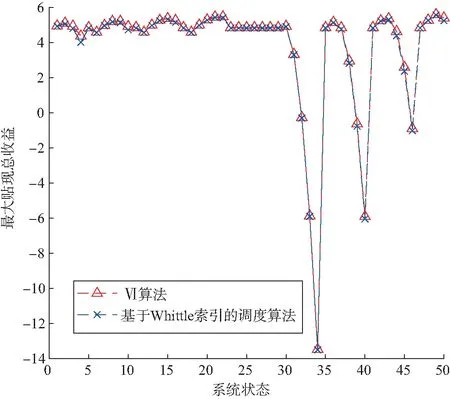
图2 值迭代算法与基于Whittle索引的最优调度算法的最大贴现总收益Fig. 2 Maximum discounted total return of value iterative algorithm and the Whittle indexbased scheduling algorithm

5 结语

本文研究在分组随机到达、严格时延等约束时衰减信道下P2P的实时通信问题。引入拉格朗日数乘因子将P2P实时传输调度模型建模为RBP模型，证明P2P实时传输调度问题的可索引性，并给出基于Whittle索引的实时传输策略，极大减少了求解最优策略的计算成本。在多用户通信系统中，随着用户状态的增多，状态空间呈指数形式增长,因此，本文提出的传输模型以及处理方式，可以进一步推广到多用户P2P实时传输调度问题中，在多用户情况下仍然有运用价值。