Relationships between distribution characteristics of ceramic fragments and anti-penetration performance of ceramic composite bulletproof insert plates
Wen-ho Yu ,Wei-ping Li ,Yi-fn Shnggun ,Xin-yng Ji ,Tin M ,*,Guo-qing Wu ,**
a School of Materials Science and Engineering,Beihang University,Beijing,100191,China
b Institute of Quartermaster Engineering Technology of PLA Academy of Military Science,Beijing,100010,China
c China Linyi High-tech Zone Shuanghang Material Technology Co.,Ltd.,Linyi,276000,China
Keywords:Bulletproof insert plate Ceramic fragment Statistic Energy absorption Anti-penetration performance
ABSTRACT Through quantitative statistics and morphological characterization of ceramic fragments for ceramic composite bulletproof insert plates (CCBIPs),distribution characteristics of ceramic fragments within a specific size range were analyzed for different Armor Piercing Incendiary (API) and shot times.To quantitatively evaluate the effect of energy absorption for ceramic plates,a model of energy absorption during penetration for CCBIPs was established based on statistics of the size distribution of ceramic fragments (SDCF).Variation in the SDCF and its influence on energy absorption for CCBIPs were investigated.The results indicate that the distribution feature of ceramic fragments in the range of 0.25-2.25 mm is Gaussian distribution.Compared with Type 56 of API (56-API),ceramic fragments formed by 53-API with higher kinetic energy possess more quantity and more concentrated distribution,whose average equivalence size decreases by 6.5%,corresponding to increasing by 83.9% of estimated energy absorption.Besides,the ability of CCBIPs to resist the third shot is significantly weakened,whose estimated energy absorption decreases by 58.8% compared with the first shot.More concentrated distribution and fewer fragments are formed after the third shot,the average equivalence size of ceramic fragments increases by 6.9%,which may attribute to the micro-cracks induced by the previous two shots.
1.Introduction
In modern warfare,ceramic composite armor system has become a critical object for improving the security and maneuverability [1,2].Ceramic materials such as Al2O3,B4C and SiC are often used as the front plate due to their low density,high hardness and compressive strength [3-5].The impact energy is first absorbed by the ceramic plate to resist the penetration of projectiles and mitigate the damage to the human body [6].The quantitative evaluation of its anti-penetration performance has become one of the concerns.
Many works have been done to improve the impact resistance of ceramic composite armor.Meanwhile,the ballistic limit velocity,ballistic efficiency and depth of penetration are commonly used to evaluate the anti-penetration performance[7-9].For a given areal density,the ballistic limit velocity of ceramic composite plates can be more effectively accelerated by the increasing thickness of the SiC layer than that of the backing plate [10].With the increase of purity,99.5% grade Al2O3exhibits a predominant transcrystalline fracture and higher ballistic efficiency factor compared with 99.5%grade Al2O3[11].By means of spark plasma sintering,the commercial B4C ceramic is toughened by graphene platelets,and the average penetration depth decreases from 2.3 mm to 1.4 mm [12].In addition,the pre-stress,thin membrane restraint and supporting backplates are also reported [13-15].
In general,the guiding principle for improving the antipenetration performance of armor materials is to maximize their energy absorption[16].The quasi-static compression test is carried out for the ceramic panel,and the area under the experimental force-displacement curve is measured as its energy absorption[17].Liu et al.[18]obtained the relationship between the kinetic energy of projectile and penetrating time by numerical simulation.The reduction of kinetic energy while penetrating the ceramic cylinder layer is regarded as its energy absorption.Liu et al.[19]thought that the liquid-phase sintered SiC specimen might absorb more energy due to its more concentrative broken area compared to that of the solid-state sintered specimen.Madhu et al.[11]found that ceramic tiles are broken into a larger number of finer fragments with the increase of impact velocity,which may lead to more efficient energy absorption.Zhang [20] obtained the spatial distribution of fragments in a specific range by numerical simulation.Liang [21]designed the breadth-first search algorithm to predict the number and size of fragments.Bond et al.[22] proposed an energy absorption model,the energy absorption of ore crushing is inversely proportional to the square root of the diameter of crushing products.After the anti-penetration test,a large number of ceramic fragments are formed at the impact point.Mining the practical information of these fragments and establishing the relationships between them and energy absorption during penetration are expected to provide a new basis for quantitative analysis of the antipenetration performance for CCBIPs.
Abbreviations
APIArmor Piercing Incendiary
CCBIPCeramic composite bulletproof insert plate
FWHMFull width half maximum
SDCFSize distribution of ceramic fragments
SDCF53-1SDCF induced by the 1st shot of 53-API
SDCF53-3SDCF induced by the 3rd shot of 53-API
SDCF56-1SDCF induced by the 1st shot of 56-API
53-APIType 53 of Armor Piercing Incendiary
56-APIType 56 of Armor Piercing Incendiary
In this paper,in order to quantitatively evaluate the energy absorption effect of CCBIPs in the anti-penetration test,quantitative statistics and morphology characterization are carried out for ceramic fragments.The size distribution characteristics of ceramic fragments in the range of 0.25-2.25 mm obtained from antipenetration tests subjected to different projectiles and shot times are analyzed.The model of energy absorption is established based on statistics of the SDCF.Combined with the micromorphology of ceramic fragments,the variation rule of SDCF and its influence on the energy absorption effect of the ceramic plates in the antipenetration test are discussed to provide a new idea for quantitative evaluation of the anti-penetration performance for CCBIPs.
2.Experimental materials and methods
2.1.Materials
2.1.1.Ceramic composite bulletproof insert plates
The size of the CCBIP is 300×250×18 mm.It is composed of a hot-pressed sintered SiC ceramic with a thickness of 8 mm and an ultra-high molecular weight polyethylene fiber backplate with a thickness of 10 mm.
2.1.2.Projectiles
The projectiles used in the test and related parameters are shown in Table 1.Compared with the 56-API,the 53-API has greater mass and higher impact velocity,which means that the 53-API has more kinetic energy.At the same time,the length of the 53-API is larger than that of the 56-API.It can be inferred that the wearing history between the 53-API and the CCBIP is more extended during the anti-penetration test.
2.2.Anti-penetration test
The anti-penetration test is carried out following “GJB4300A-2012 Requirements of Safety Technical Performance for Military Body Armor”.The ceramic plate is fixed in front of the clay witness.There is photoelectric door 1,photoelectric door 2,CCBIP and clay witness along the shooting direction.The schematic diagram of the test equipment is shown in Fig.1.CCBIPs were heated at 55°C for 8 h.The shooting scheme designed for each CCBIP is shown in Table 2.
An auxiliary device is set in front of the CCBIP to block and collect the spattering ceramic fragments.After every shot,the CCBIP is removed,and ceramic fragments remained at the impactpoint are poured into a container.The smaller ceramic powders attached to the auxiliary device and impact point are collected by brushes and poured into the container.Ceramic fragments collected after every shot are put into a transparent bag,and the corresponding test condition is marked.

Table 1 Type of projectiles and related parameters.
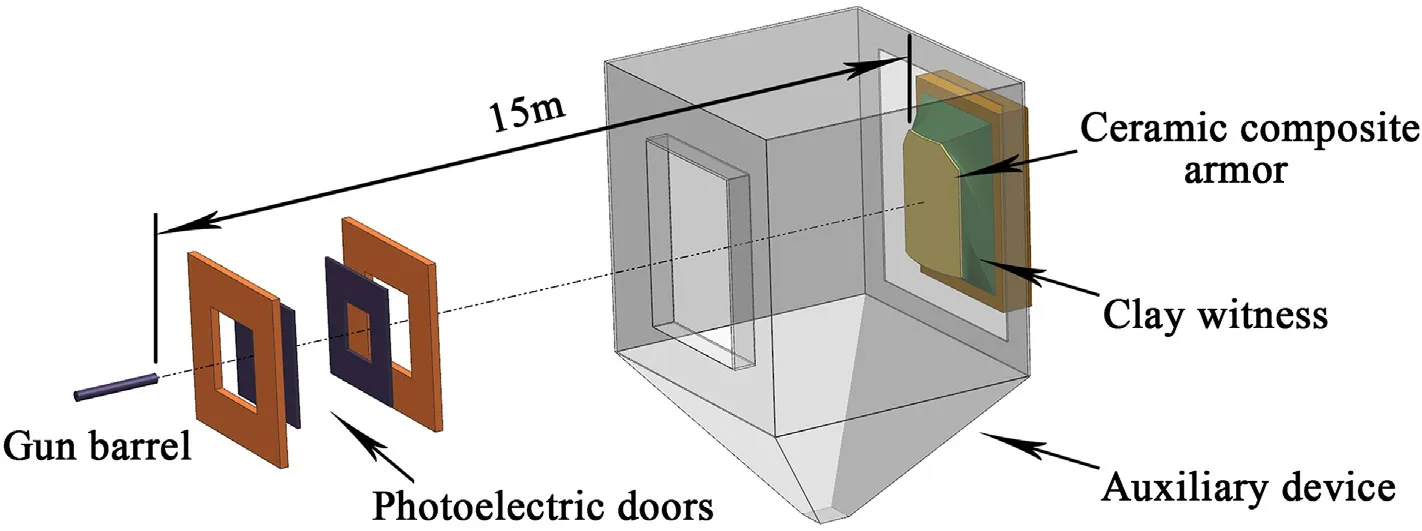
Fig.1.Schematic diagram of anti-penetration test equipment.
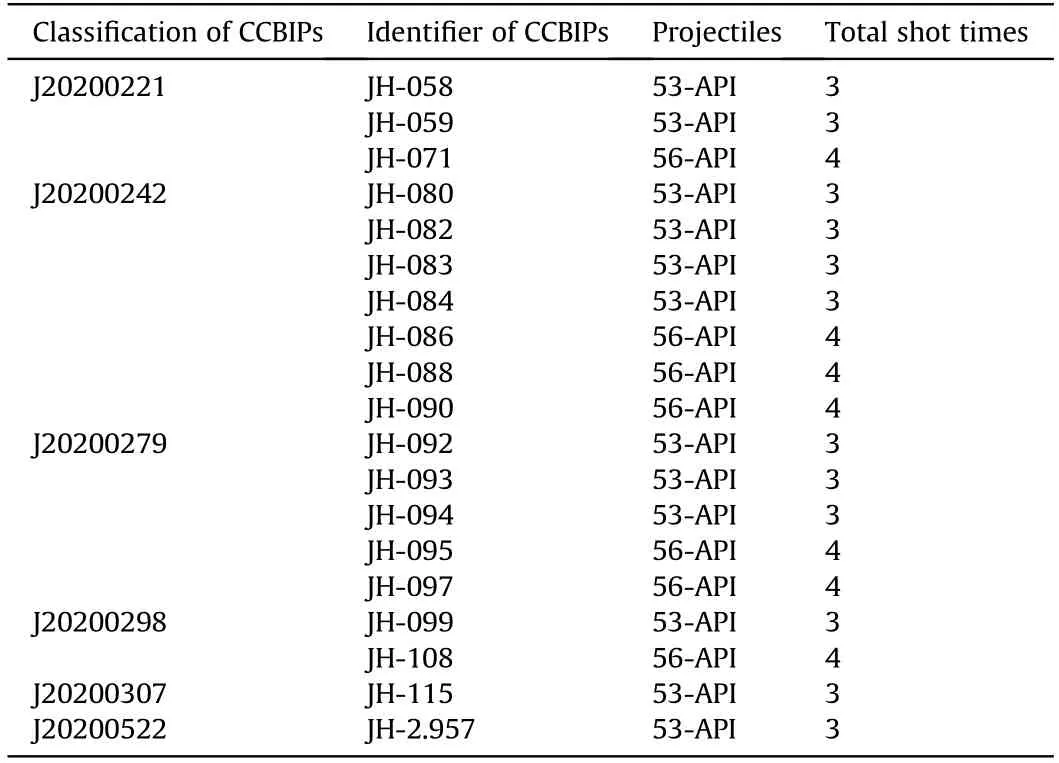
Table 2 Summary of the classification,identifier and shooting scheme of CCBIPs.
2.3.Characterization method
Tile the ceramic fragments on the white background desktop,put a ruler as the scale,use a 25X automatic optical microscope to take pictures(see Fig.2),and use a hand-held optical microscope to observe the size characteristics of typical ceramic fragments (see Fig.3).The micromorphology of ceramic fragments obtained from the anti-penetration test was observed by Phenom ProX scanning electron microscope.
2.4.Statistical methods

Fig.2.Photograph of partial ceramic fragments.

Fig.3.Dimensional characteristics of typical ceramic fragments.
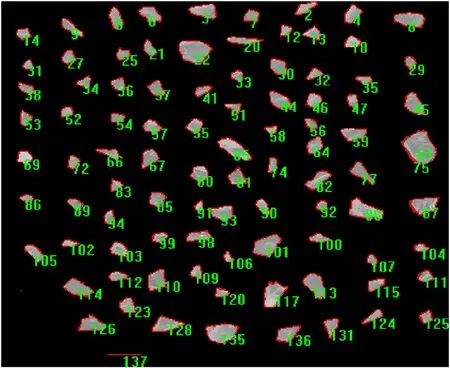
Fig.4.Measurement of two-dimensional size for ceramic fragments.
Standard sieves with mesh sizes of 2 mm,0.84 mm,and 0.42 mm were used in sequence to screen the ceramic fragments,and the ceramic fragments left on the sieves were selected as the statistics object.As shown in Fig.4,the data of each ceramic fragment is processed by the software.First,the long axis and short axis of each ceramic fragment passing through the center of mass are measured,then selected 480 ceramic fragments (Sample A)randomly from them to gauge their corresponding thickness c,respectively.The three-dimensional model of the ceramic fragments is shown in Fig.5.Attempt to establish the relationship between the two-dimensional size and the thickness of the fragments to estimate the three-dimensional equivalent size of the ceramic fragments more quickly and accurately.
Five expressions f(a,b) were defined as the two-dimensional equivalent size of ceramic fragments.Assume that c=kf(a, b),where k is a variable about f(a,b).The f(a,b)and the corresponding k value of each ceramic fragment in sample A were statistically analyzed.According to the range of f(a,b),they were evenly divided into 20 intervals.The center of each interval was taken as the independent variable,and the average k value of the ceramic fragments in each interval was taken as the dependent variable.The relationship between k and f(a,b) was attempted to fit with different functions based on the measured data of Sample A,and the functional relationship model and fitting accuracy are shown in Table 3.
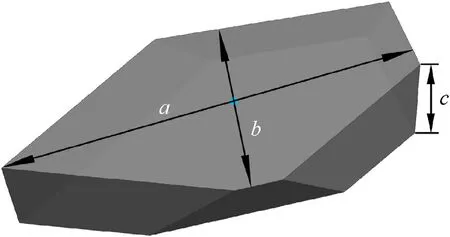
Fig.5.Three-dimensional model of the ceramic fragment.
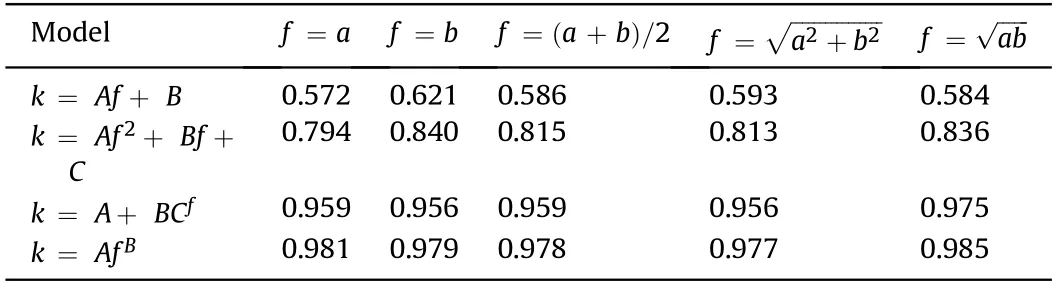
Table 3 Model and fitting accuracy of three-dimensional relationship for ceramic fragments.
Then the thickness c of ceramic fragments can be estimated approximately by formula (1),that is:

The three-dimensional equivalent size of the ceramic fragments is substituted with.According to the relationship between c and ab,the equivalent size x of the ceramic fragment is as follows:

According to the statistical results of the equivalent size x of all ceramic fragments,the ceramic fragments with the equivalent size ranging from 0.25 mm to 2.25 mm were evenly divided into 20 intervals.The center of each interval was taken as the independent variable,and the quantity of ceramic fragments in each interval was counted as the dependent variable.The Gaussian distribution function is used to fit the relationship between equivalent size (x)and corresponding quantity (y) of ceramic fragments,and the functional relationship is as follows:

The fitting result of the size distribution for ceramic fragments collected at a specific impact point is shown in Fig.7.
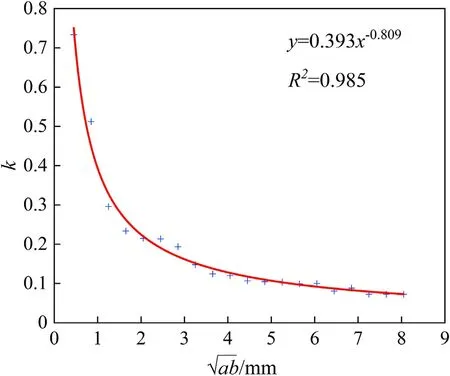
Fig.6.Fitting result of the three-dimensional relationship model for ceramic fragments.
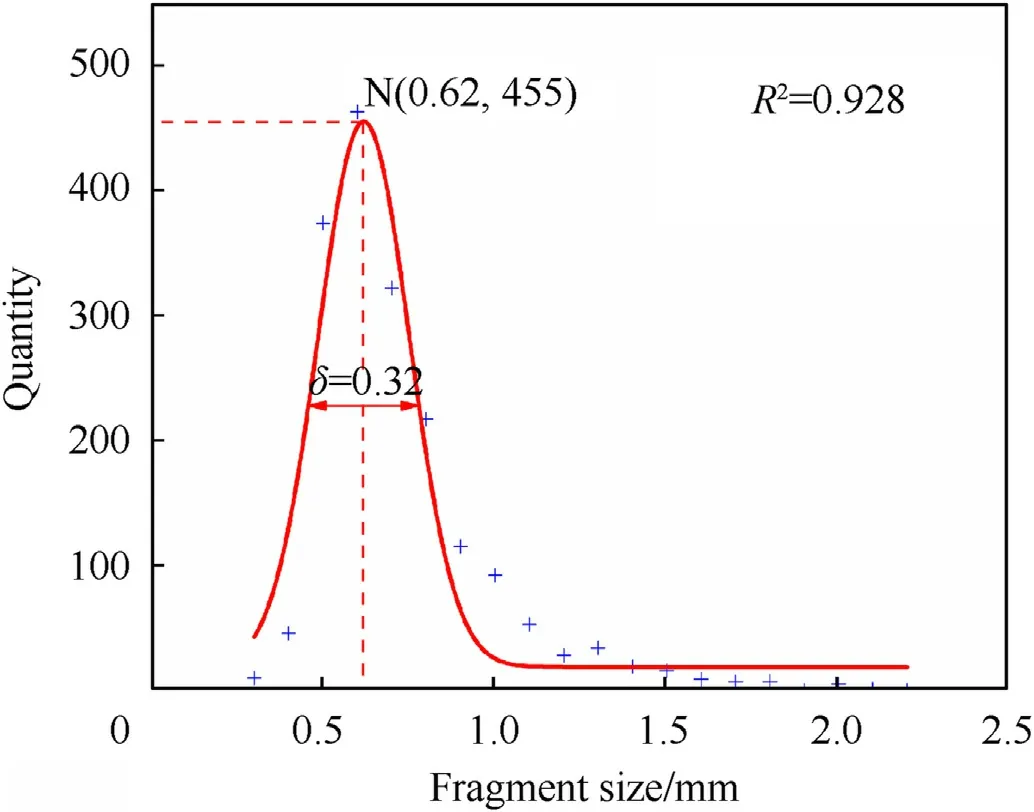
Fig.7.A typical result of Gaussian fitting for the size distribution of ceramic fragments.
3.Results and discussion
According to the statistical and preliminary analysis,63 (64 in total)groups of Gaussian fitting accuracy R2were above 0.870.The fitting accuracy R2of the size distribution for ceramic fragments induced by the 1st shot of the JH-115 plate is 0.721,which may be due to the omission in the manual collection of ceramic fragments.It will not be used in the subsequent analysis.
3.1.Establishment of the model of energy absorption during penetration for CCBIPs
Based on the following physical assumptions,the model of energy absorption for CCBIPs is established:
1) Rigid projectiles impact the rigid ceramic plates quickly.
2) The kinetic energy of API is partially converted into the energy absorbed by the CCBIP,and the rest is lost to heat the API and CCBIP,and the plate loading device will not slosh or absorb the energy.
3) The energy absorbed by the ceramic plate is consumed in the process of ceramic crushing.
4) Based on the third theory of Bond et al.[22],the energy absorbed during crushing of the ceramic plate is inversely proportional to the square root of the equivalent size of the ceramic fragments.For each ceramic fragment:

Where E is the energy absorbed to form the ceramic fragment,Dfis the equivalent size of the crushed objects (total fragments),Dqis the equivalent size of the crushed product(a single fragment),and K is the proportional coefficient.
If a total of R tests are carried out under the same test conditions,each test is represented by r(r=1,2…R);for the ceramic fragments produced in each test,each size interval is represented by q(q=1,2… 20);The quantity of ceramic fragments in the qth interval produced by the rth test is represented by yr,q,and the equivalent size of ceramic fragments in each interval xr,qis substituted with the center of the interval,as follows:
According to the fitting result of Gaussian distribution,the quantity of ceramic fragments in each interval can be obtained as follows:

Where y0、A、xcand ω are all function parameters obtained by Gaussian fitting.
Average fitting results under the same test conditions can be obtained as follows:
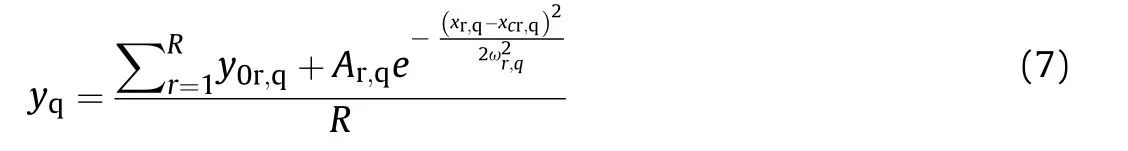

For a specific test condition,the equivalent size of the crushed products in the qth interval is expressed as:Since the total volume of ceramic fragments before and after crushing is equal,the equivalent size of total ceramic fragments under a specific test condition is:

When there is only one test condition variable (projectiles or shot times)to compare the energy absorption effect,assuming that the proportional coefficient K is 1,the estimated energy absorption(Ea) of ceramic plates can be expressed as:

Based on the statistics of the size distribution of ceramic fragments obtained from the anti-penetration test,the calculation model was established to estimate the energy absorption for CCBIPs during penetration.This paper will discuss and analyze the energy absorption effect of the CCBIPs under different test conditions based on this model.
3.2.Impact of different API on the energy absorption effect of CCBIPs
As shown in Table 2,seven homogenous CCBIPs classified by the“J2020242”are regarded as typical representatives.The parameters and fitting precision R2obtained by Gaussian fitting of the corresponding SDCF were analyzed on the condition that 53-API and 56-API were used for the 1st shot.Gaussian fitting results are shown in Table 4.The fitting accuracy R2has reached above 0.9,values of the other parameters can be used to fit the SDCF,as shown in Fig.8.
The dotted line in Fig.8 shows the SDCF formed by the 1st shot for each plate with 53-API and 56-API.The solid line (SDCF53-1,SDCF56-1)is the average result of the SDCF under the corresponding test conditions.For 53-API and 56-API,the average results also conform to Gaussian distribution,which act as the critical basis for analyzing the relationships between characteristics of the SDCF and energy absorption effect of the CCBIPs subjected to different projectiles.
SDCF53-1and SDCF56-1not only reflect the difference on theFWHM (δ) and peak coordinate (xm,nm),but also can be used to estimate the total quantity of ceramic fragments (n) and average sizeunder the corresponding test conditions.The total quantity of ceramic fragments under the corresponding test conditions is calculated as follows:

Table 4 Gauss fitting results of the SDCF subjected to the 1st shot with different projectiles.
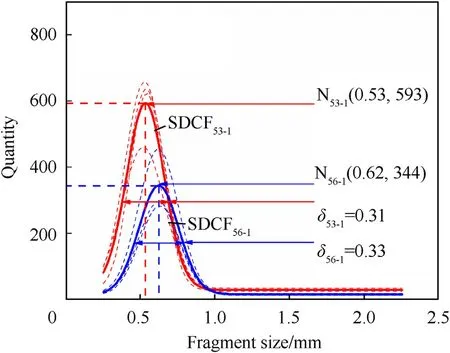
Fig.8.Typical curves of the SDCF induced by the 1st shot with 53-API and 56-API.

The average size of ceramic fragments under the corresponding test conditions is calculated as follows:

According to the model of energy absorption for the CCBIP,the estimated energy absorption corresponding to SDCF53-1and SDCF56-1is calculated,respectively.The characteristic parameters of the SDCF and estimated energy absorption induced by the 1st shot of different projectiles are shown in Table 5.
Compared with SDCF56-1,the FWHM (δ) of SDCF53-1is smaller,which implies SDCF53-1is more concentrated.Additionally,the concentration position(xm)of SDCF53-1is more to the left than thatof SDCF56-1.Compared with SDCF56-1,the total quantity of ceramic fragments increases by 66.6%,and their average size decreases by 6.5% for SDCF53-1.It may be related to the more incredible kinetic energy and longer warhead of the 53-API.The higher projectile velocity (kinetic energy) corresponds to the more significant half cone angle of the ceramic crushing cone and greater penetration depth [10,23].Compared with the 56-API,the 53-API has greater kinetic energy and more substantial penetrating power for CCBIPs.As a result,the ceramic cone formed by 53-API has a larger volume,corresponding to a more considerable volume of total ceramic fragments.Furthermore,53-API has a more significant warhead length.It implied that the wearing history between 53-API and the CCBIP is longer.Therefore,more extensive and smaller ceramic fragments are formed,corresponding to the increase in quantity and reduction in their average size.

Table 5 The characteristic parameters of the SDCF and estimated energy absorption corresponding to the 1st shot with 53-API and 56-API.
As shown in Table 5,the estimated energy absorption (Ea) corresponding to SDCF53-1has increased by about 83.9% compared with SDCF56-1.That is closely related to the characteristics of different projectiles.The ceramic cone formed by the high kinetic energy projectiles (53-API)has a larger volume,which also means the increase of the equivalent size (Df) of the total ceramic fragments mentioned in Eq.(10).At the same time,SDCF53-1indicates the formation of more fragments concentrating in a smaller size range (xmis smaller).In other words,compared to 56-API,the quantity of ceramic fragments(yq)in the smaller fragment size(Dq)range formed by 53-API increased significantly in the 1st shot.Ceramic fragments in this range are the main contribution to the estimated energy absorption.The increase in their quantity (yq)further caused a rise in the estimated energy absorption.It can be considered that the core materials play an important role in the propagation of stress waves.As shown in Table 1,the hardened steel is used for the core material of 53-API,whose hardness is higher than that of mild steel used for 56-API.The deformation of the core with higher hardness would be lower than that of the softer core during penetration [24].Meanwhile,less deformation also makes the kinetic energy distribute in a smaller area,and more energy would be absorbed by the ceramic plate.That is consistent with the higher estimated energy absorption corresponding to the SDCF53-1.
Therefore,compared with 56-API,the quantity of ceramic fragments formed in the 1st shot with 53-API is more extensive,the average size is smaller,and the SDCF is more concentrated.Variation of SDCF corresponds to the difference in the penetration behavior of 53-API and 56-API.Most importantly,it also corresponds to the rising estimated energy absorption of CCBIP induced by 53-API.Therefore,the energy absorption effect of the CCBIP subjected to different projectiles can be evaluated according to the variation of SDCF.
3.3.Influence of different shot times on energy absorption effect of CCBIPs
As shown in Table 2,the first four homogenous CCBIPs classified by the “J2020242” are regarded as typical representatives.The parameters and fitting precision R2obtained by Gaussian fitting of the corresponding SDCF were analyzed on condition that 53-API was used for the 1st and the 3rd shot.The results are shown in Table 6.The fitting accuracy R2has reached above 0.9,other parameters were used to fit the SDCF,as shown in Fig.9.
The dotted line in Fig.9 shows the SDCF formed by the 1st and the 3rd shot for each plate with 53-API.The solid line is the average result of the SDCF under the corresponding test conditions.The average results (SDCF53-1and SDCF53-3) also conform to Gaussian distribution,which act as the critical basis for analyzing the relationships between characteristics of the SDCF and energyabsorption effect of CCBIPs under different shot times.
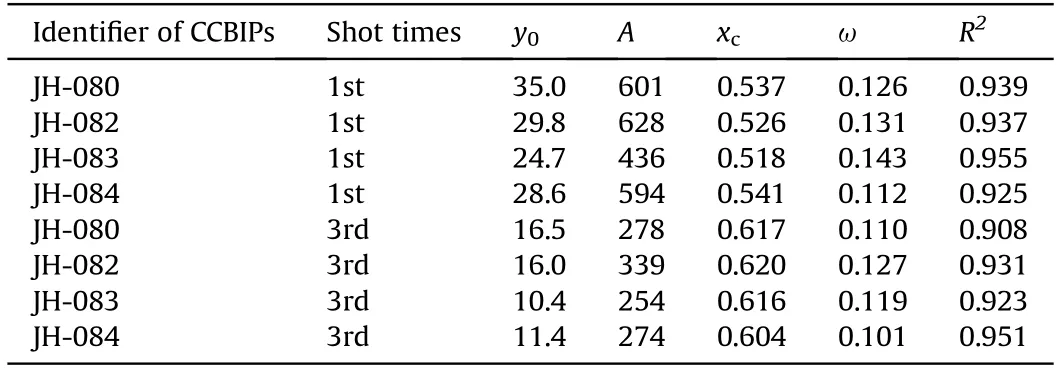
Table 6 Gaussian fitting results of the SDCF subjected to 53-API under different shot times.
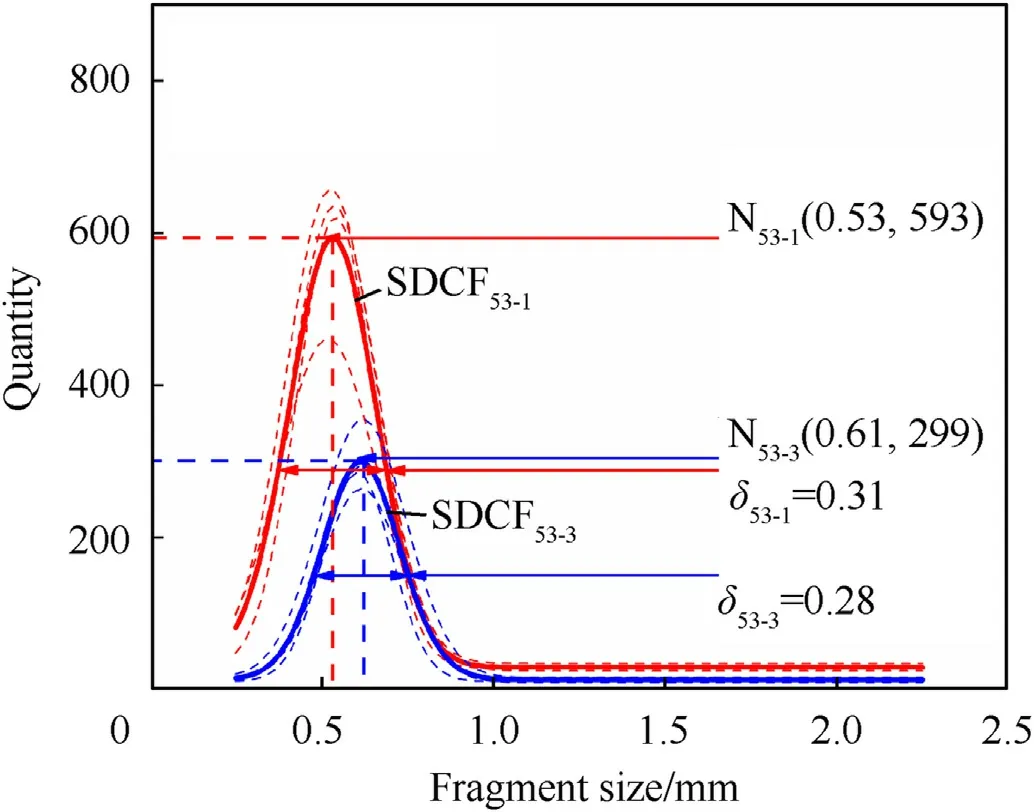
Fig.9.Typical curves of the SDCF induced by the 1st and the 3rd shot with 53-API.
According to Eqs.(11) and (12),the total quantity (n) and average sizeof ceramic fragments under corresponding test conditions are calculated.The estimated energy absorption is calculated according to the model of energy absorption for the CCBIPs,corresponding to SDCF53-1and SDCF53-3,respectively.The characteristic parameters of the SDCF and estimated energy absorption induced by 53-API under different shot times are shown in Table 7.
Compared with SDCF53-1,the FWHM (δ) of SDCF53-3is smaller,which implies SDCF53-3is more concentrated.Additionally,the concentrated position (xm) of SDCF53-3is more to the right than SDCF53-1.Compared to the 1st shot with 53-API,the quantity of ceramic fragments formed in the 3rd shot decreases by 53.8%,and the average size of ceramic fragments increases by 6.9%.It may be related to the micro-cracks induced by the stress waves in the first two shot.The typical micro-cracks in the ceramic fragments induced by the 1st shot are shown in Fig.10.It is speculated that these micro-cracks provide a favourable path for crack propagation during the 3rd shot.The extension of the crack propagation path makes the dissociation surface larger and the average size of ceramic fragments larger.At the same time,the existence of micro-cracks reduces the continuity of the structure,the transmission range of the stress waves between the structures is reduced.Reducing the affecting domain of stress waves also means decreasing the volume of the total ceramic fragments before crushing.Reduction of the volume of total ceramic fragments combined with the increase of their average size lead to the decreasing quantity of ceramic fragments after the 3rd shot.

Table 7 The characteristic parameters of the SDCF and estimated energy absorption induced by the 1st and 3rd shot with 53-API.

Fig.10.Typical characteristics of micro-cracks in SiC ceramic fragments induced by the 1st shot with 53-API.
As shown in Table 7,the estimated energy absorption of SDCF53-3 is about 58.8% lower than that of SDCF53-1,closely related to the characteristics of the SDCF under different shot times.Compared with the 1st shot,the volume of total ceramic fragments decreased under the 3rd shot,which corresponds to the decrease of Dfin the model of energy absorption.At the same time,SDCF53-3indicates that the ceramic fragments are more concentrated in a larger size range (xmis larger) compared with SDCF53-1.It means that the estimated energy absorption for the 3rd shot with 53-API mainly comes from ceramic fragments in a larger size (larger Dq).Furthermore,the quantity (yq) of those fragments decreases obviously.Finally,they collaboratively result in the lower estimated energy absorption for the 3rd shot with 53-API.It can be concluded that the ceramic plate is pre-fragmented due to the transmission of stress waves in the first two shots.The ceramic plate is made more prone to brittle fracture due to these micro-cracks.Meanwhile,the ceramic fracture mechanism becomes less effective in the energy absorption performance after the first two shots [25].That is consistent with the lower estimated energy absorption corresponding to the SDCF53-3.
It can be seen that compared with the 1st shot of 53-API,the quantity of ceramic fragments formed by the 3rd shot is less,the average size is larger,and SDCF is more concentrated.Variation of the SDCF may be related to the micro-cracks formed by the action of stress waves during the first two shots.More importantly,it also corresponds to the decrease of energy absorption of CCBIPs during the 3rd shot.The energy absorption effect of CCBIPs corresponding to different shot times can be estimated according to the variation of the SDCF.
4.Conclusion
Based on the quantitative statistics and morphology characterization of ceramic fragments formed in the anti-penetration test,the model of energy absorption was established for CCBIPs during penetration,and distribution characteristics of ceramic fragments in the range of 0.25-2.25 mm on the conditions of different projectiles and shot times were analyzed.Furthermore,variation rule of the SDCF and its influence on the energy absorption of the CCBIP were discussed.The key findings are as follows:
1) For the ceramic fragments with equivalent size in the range of 0.25-2.25 mm formed by the anti-penetration test,the size distribution characteristics can be fitted by Gaussian distribution.The fitting accuracy R2is more than 0.870.
2) Compared with 56-API,ceramic fragments formed by the high kinetic energy projectiles (53-API) are more extensive in quantity,smaller in average size (decrease by 6.5%) and more concentrated in size distribution,which corresponds to a higher estimated energy absorption (increase by 83.9%).
3) Compared with the 1st shot,the ability of CCBIPs to resist the 3rd shot is significantly weakened,whose estimated energy absorption decreases by 58.8%.More concentrated distribution and fewer fragments were formed after the 3rd shot,and the average equivalent size of ceramic fragments increased by 6.9%.It may attribute to the micro-cracks induced by impact waves in the first two shots.4) Variation of the SDCF is closely related to the energy absorption effect of the CCBIP during penetration.By establishing the relationship model between the characteristics of SDCF and the energy absorption during penetration for CCBIPs,it provides the possibility for estimating the anti-penetration performance of CCBIPs quantitatively.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work is financially supported by the National Key Research&Development Project (2017YFB1103505) and the Military Logistics Research Program (XXXC002) of China.
- Defence Technology的其它文章
- Experimental and numerical analysis on suitability of S-Glass-Carbon fiber reinforced polymer composites for submarine hull
- Damage response of conventionally reinforced two-way spanning concrete slab under eccentric impacting drop weight loading
- Analysis and design for the comprehensive ballistic and blast resistance of polyurea-coated steel plate
- Positive effects of PVP in MIC: Preparation and characterization of Al-Core heterojunction fibers
- Flight parameter calculation method of multi-projectiles using temporal and spatial information constraint
- Numerical simulation of drop weight impact sensitivity evaluation criteria for pressed PBXs

