面向深度学习算子的循环不变式外提算法
梁佳利,华保健,吕雅帅,苏振宇
1.中国科学技术大学软件学院,合肥230000
2.中科寒武纪科技股份有限公司,北京100000
TVM(tensor virtual machine)[1]是一个开源深度学习编译器[2-5],通过提供图级别的优化[6]和算子级别的优化,生成多硬件后端代码。在算子实现时,不同的计算方法却导致了生成代码的局部性、并行性的差异[7-8]。TVM 的领域专用语言——张量表达式支持用简洁的方式定义算子,并提供一系列调度原语对算子代码做循环变换。用张量表达式描述的算子会被TVM翻译为TVM IR(TVM intermediate representation)——一种树状的、易于描述循环计算的高级中间表示。TVM 在TVM IR 上实现了一系列分析和变换的优化遍,来对算子的中间表示进行调整和优化,最终生成目标硬件平台上的高效代码。
深度学习应用[9-12]中的重要算子,如卷积、矩阵乘和向量加等,都会被TVM 编译生成TVM IR 上的多层嵌套循环[13],经过循环变换后会产生与循环迭代变量相关的复杂表达式计算。例如,以下的代码示例是向量加算子的TVM IR 表示:
1.for(i.outer:int32,0,4){
2.for(i.inner:int32,0,32){
3.C[(i.outer*32)+i.inner]=
4.A[(i.outer*32)+i.inner]+
5.B[(i.outer*32)+i.inner]}}
注意到在内层循环中存在被重复计算的表达式i.outer * 32,它应该被循环不变量外提优化[14]提取到第一层和第二层循环之间,从而消除冗余计算。
然而,在深度学习编译器中实现循环不变式外提优化,存在以下研究挑战:
首先,传统编译器中的循环不变量外提优化算法,将计算结果保存在物理寄存器中,避免每次使用时都重复计算。但是TVM 等深度学习编译器的高级中间表示无法感知物理寄存器的存在,盲目地外提所有循环不变量会带来不必要的寄存器压力,甚至降低算子的性能[15];因此直接将传统编译器中的循环不变式外提算法应用到TVM 等深度学习编译器中,并不能得到理想的优化效果。
其次,表达式中操作数的顺序会影响不变式的发现[16];传统的循环不变式外提算法,对深度学习算子中经常出现的、复杂嵌套条件表达式的检测能力有限,无法检测、合并、变换生成新的循环不变式。
最后,深度学习编译器生成的算子,会被目标平台编译器进一步编译优化。目标平台编译器在一个更低级的中间表示上进行优化[17],而在两个不同级别上的优化常常存在冲突[18],导致降低了循环不变式外提算法的有效性。Halide 开源编译器[19]中实现了一个保守的循环不变式外提算法,但该算法只考虑循环内的表达式,而不对语句做处理;且在做循环不变式外提之前只对包含加减法的表达式做了重结合,没有对条件表达式做优化;因此,这些简单的处理并不能完全解决上述研究挑战。
本文提出了一种面向深度学习编译器高级中间表示的、采用启发式策略的循环不变式外提算法。首先,针对第一个研究挑战,本文借鉴Halide 编译器循环不变量外提优化的代价模型,设计了衡量表达式计算代价的函数,来指导是否外提循环不变式,以一种简单且易于实现的方式对消除冗余计算和寄存器分配之间的矛盾做了权衡。其次,针对第二个研究挑战,本文算法在检测循环不变量之前,先调整操作数结合顺序和变换条件表达式的形式来对表达式做规范化,为循环不变量外提优化以及后续的其他优化提供更好的时机。最后,针对第三个研究挑战,本文结合TVM IR 和目标平台编译器的具体特点,对分支和迭代数目比较小的内层循环做了特殊处理,解决了在不同级别的中间表示上的优化冲突。
为验证本文算法的有效性,在开源编译器TVM的0.7 版本上实现了本文算法,并进行了实验和结果分析。实验选择TVM 的TOPI测试集作为测试集合,对其包含的27 个算子对应的511 个测例进行了测试,这些算子都是TVM 框架频繁用到的算子,其中包含了多种实现策略的卷积和激活等算子,测例都是典型的多层嵌套循环的数组计算,同时一些算子内的补零和边界检查操作在循环内产生了条件表达式和分支。这些算子测例描绘了常见深度学习领域算子特点,并且每一个算子都提供了大量在常见神经网络中不同参数规模的测例,因此具有一定的代表性。实验结果发现,在排除那些优化前后代码没有发生变化的测例后,与未进行循环不变量外提优化的测例相比,有47.6%的算子性能得到了显著提升,最大加速比大于40.0%;所有测例的总时间加速比平均为22.7%。实验结果证明,本算法对TVM 生成算子的性能产生了积极影响,加速了含有大量冗余计算的算子的执行,完善了TVM 的算子优化。
总结起来,本文的主要贡献如下:
(1)提出了一个新的融合深度学习代价函数和启发式策略的循环不变量外提算法;
(2)基于TVM 开源深度学习编译器(0.7 版本),给出了原型系统设计与实现;
(3)选取深度学习领域典型的27 个算子及其511个测例,对原型系统进行了系统测试;实验结果分析表明,该算法对提升TVM 的性能产生了积极作用。
1 背景与研究动机
本章介绍关于TVM 中间表示的相关背景,以给出本文工作的研究动机。
1.1 张量表达式和TVM IR
张量表达式是TVM 基于Halide 的算子描述和调度优化分离的思想[7-8],而设计实现的描述张量运算的领域专用语言。该语言定义张量间的输入输出关系,同时提供循环拆分、循环合并和循环分块等一系列调度原语,这些调度原语的组合指定了计算输出张量的具体策略[20]。
张量表达式首先被翻译为TVM IR,TVM IR 是一种树状的中间表示,主要包含两种类型的节点:(1)表达式节点;(2)语句节点。表达式节点主要包含:有名字的变量和常数、数组数据的加载、函数调用、算术逻辑表达式、条件表达式等;语句节点包含顺序、循环、分支、赋值等。
下面实例定义了一个描述固定规模矩阵乘法算子的张量表达式:

变量A、B为规模为(1 024,1 024)的二维矩阵,k为求和归约的那个循环“轴”。矩阵C由矩阵A和B计算得到。上述算子被翻译为以下TVM IR:
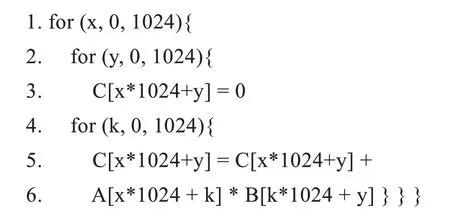
为了高效实现上述代码中的最内侧循环,TVM使用了tile、split和reorder等操作,对矩阵乘法算子进行循环分块、循环拆分和循环重排序:

1.2 研究动机
算子经过循环变换后有更好的并行性和数据局部性,且能够充分利用底层硬件特性,加速计算[7,13,20-22]。但是算子经过循环变换后,数组下标表达式变为了语义等价,但更复杂的表达式,增加了额外标量运算。例如上述矩阵乘算子最后生成的TVM IR,对于最内层循环,其循环迭代变量是yi,下标表达式xo*32768+xi*1024+yo*32 在最内层循环迭代时,计算结果不变,在第一次迭代后的计算都属于冗余计算。本算法的设计目标,是通过把循环中多次迭代结果保持不变的计算移动到循环外,从而减少冗余计算。另外,TVM 编译生成的算子会经过目标平台编译器的编译优化,才能在常用深度学习硬件,如英伟达的GPU 和寒武纪的MLU 硬件上[23],高效运行。这类硬件的典型特征是很多部件都为了运行计算密集的程序而设计。为了充分利用这些硬件特性,目标平台编译器会选择展开内层循环,一些计算的延时通常被指令流水线所掩盖,因此一些冗余计算并不影响运行时间,反而会降低物理寄存器压力。而由于硬件更专注于计算,对于分支优化处理的任务需要由编译器优化完成[24-25]。因此对布尔表达式、条件分支语句进行外提时需要谨慎处理,有时还需要变换条件表达式的形式,使得生成的代码更利于底层编译器的优化。综合以上讨论,本文面向深度学习编译器,提出了一种新的循环不变量外提算法,该算法考虑了TVM IR 和目标平台编译器的特点,通过外提循环不变量减少冗余计算,提高TVM 生成算子的性能。
2 相关工作
作为优化循环内冗余计算的一种有效技术,循环不变式外提已经被广泛研究和应用,很多编译器都使用消除冗余计算的方法,优化生成代码性能。Aho 等[14]系统讨论了循环不变量外提的概念。TVM[1]在图级别的中间表示RELAY 上[6],使用公共子表达式消除算法,在算子的层级上减少了相同输入规模算子的重复计算;LLVM(low level virtual machine)[26]在LLVM IR 上使用了循环不变量外提技术,在基于基本块的控制流图上对循环内不变量指令外提;Steffen 等[27]提出了一种代码移动和代数优化的算法;Rosen 等[28]使用全局值编号来做冗余消除优化。但是,这些研究都是做语义更高的计算图级别中间表示,或是语义更低的底层中间表示上进行,缺失了在像TVM IR 这种源代码级别的树状中间表示上的优化算法。如RELAY 中间表示上没有循环的概念,对于RELAY 的冗余消除优化都是以整个算子为单位,优化的粒度过大,并不能很好地对算子内的计算进行优化。如在LLVM IR 上的循环不变量外提技术在一个更低级别的中间表示上进行,并没有对于高语义的表达式形式如嵌套的条件表达式提供优化方案。因此这些方法无法直接应用在深度学习编译器的优化场景中。不少的研究对于源代码级别的优化做了讨论和实践。Halide 编译器[19]在把算子计算描述翻译为Halide IR 后,针对循环内的表达式使用了公共子表达式删除和循环不变量外提技术。Rawat等[15]提出了一个寄存器优化框架,在源代码级别对含有多层嵌套循环的高阶模板计算进行了寄存器的优化,提高指令并行性;akg 框架[29]研究了在华为mindspore后端的算子自动生成器akg 上,实现公共子表示消除算法,优化了特定指令的重复计算;Vasilev等[30]提出了一种在递归函数上的循环不变量外提算法;Song 等[31]通过展开循环的前几次迭代,来优化循环不变量外提的效果;Bacon 等[32]全面总结了在高级语言上的高性能计算的优化方法。但是,这些研究提供的消除冗余计算的方法没有考虑到TVM 算子程序特点和深度学习加速硬件的特性。如akg 的公共子表达式消除只是针对特殊的张量指令进行,并没有对于TVM 算子调度优化产生的复杂下标表达式和条件表达式做优化。深度学习领域的处理器虽然有很好的指令集并行架构,却不擅长分支的处理。如Halide 编译器实现的循环不变式外提算法,在分支的处理上忽略了对条件表达式的优化。因此这些方法对于深度学习编译器的优化,还存在不足之处。
3 系统设计与实现
本章讨论系统的设计与实现。在给出系统架构后,重点讨论循环不变式外提算法,并给出规范化和代价函数。
3.1 系统架构
本文设计和实现的系统基于开源深度学习编译器TVM 的0.7 版本。TVM 优化[1]可以分为图级别优化和算子级别优化两个独立的模块,算子级别的优化又可分为在张量表达式级别的基于机器学习的自动调度优化和在TVM IR 级别的优化。本算法针对算子生成的TVM IR 进行优化,涉及对算子级别优化模块的修改。循环不变量外提算法在TVM 中的整体架构图和关键编译流程如图1 所示。
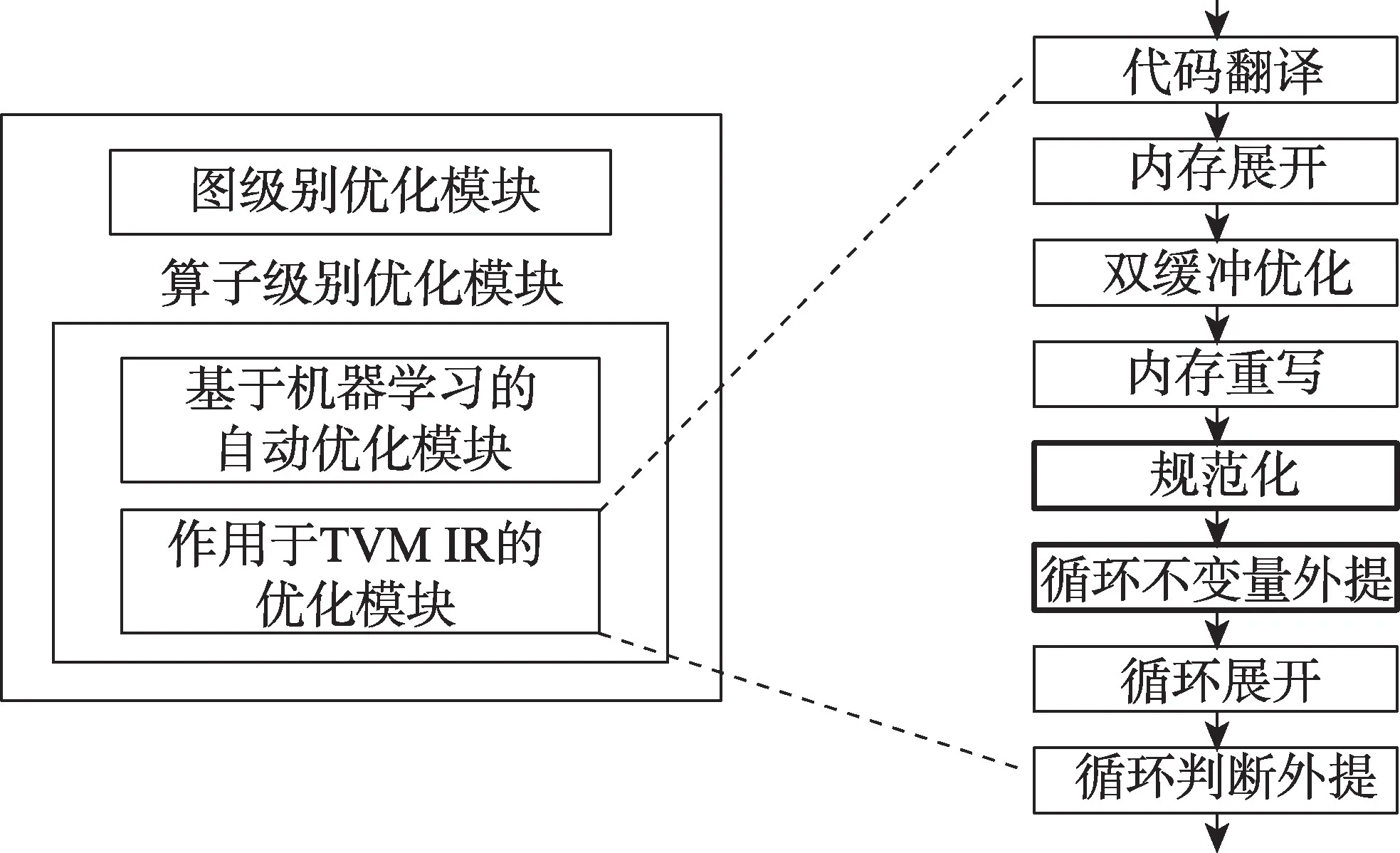
图1 TVM 中实现循环不变量外提算法的架构图Fig.1 Architecture of loop invariant code motion algorithm in TVM
从整体架构上看,循环不变量外提算法由两个关键部分组成:第一个是前处理部分规范化,该部分对表达式进行规范化处理,使得变化后的表达式更利于循环不变量的识别;第二个是不变量外提部分,对循环保持不变的表达式和语句进行识别和外提。TVM 通过优化遍管理器组织一系列优化遍在TVM IR 上进行优化,向TVM 的优化遍管理器注册本算法的优化遍,并安排新增的优化遍到原生TVM 优化遍序列的合适的位置(如图1 中加粗边框的遍所示)。同时使用了原生TVM 的循环判断外提的优化遍,对分支条件为循环不变量的分支语句做提升;修改原生TVM 的化简优化遍,禁止了原本对整数类型的赋值变量进行前向替换的操作。
大量研究表明,父母的信念是儿童信念发展的锚定起点(Ozorak, 1989; Boyatzis et al., 2006)。不同信仰的父母有着不同的观念和行为方式,这些不同借助亲子谈话等方式,影响着儿童各种观念的形成(Boyatzis et al., 2006)。 例如, Rosengren(2004)等人发现, 父母(天主教徒)被问及如何回答3~6岁的儿童的死亡问题时,大部分父母是用宗教相关的字眼来回应的,例如,天堂、灵魂、上帝等。有宗教信仰的父母的信念更加与众不同,对儿童信念的影响也显得尤为突出。
3.2 循环不变代码外提算法
深度学习编译器中的循环不变量实例中,典型的是访问数组元素的地址表达式的计算和条件表达式的计算,表达式中包含了循环迭代变量、程序参数和立即数。TVM IR 中的循环节点包含了循环嵌套关系以及对应的迭代变量,因此递归地判断某个表达式是否是循环不变的,只需要构成表达式的值满足以下判定条件:
(1)是常数(不可变的程序参数或立即数);
(2)该变量的赋值在循环之外,或者;
(3)到达该变量的使用只有一个定值,且该定值的表达式也是循环不变的。
实际上,识别在一个循环中的不变表达式,只需要标记出,在循环的多次迭代中计算结果可能发生变化的表达式,那么剩下未标记的表达式都是该循环的不变式。因此,可按照以下计算步骤识别并提升循环不变式:
(1)标记循环迭代变量为“不可提升”;
(2)标记循环迭代变量到达的定值变量都是“不可提升”;
(4)将(3)中新的变量的赋值语句插入循环之前。
虽然单个常数是循环不变的,但是提升它没有意义,因此算法不对单个常数做提升。
另外对于表达式中循环不变式的识别,表达式中操作数的顺序非常关键;不同的操作数顺序不但影响了某些循环不变的表达式能否被发现,还决定了目标编译器中某些对于分支的优化能否被触发。因此,在发现循环不变量之前需要先对表达式进行规范化,利用运算符的结合律对表达式进行重结合等变换。
算法1循环不变量外提算法

算法1 给出了循环不变式外提算法LICM(T)的伪代码。该算法接受原始程序T作为输入参数,并返回优化后的程序。算法首先调用规范化函数Normalize(T)对程序T中的语句和表达式做规范化。然后算法按照一定的顺序,遍历程序T中的语句S,并按语句S的可能语法形式进行分类讨论:若S为赋值语句x=e,并且赋值右侧表达式e被标记为“不可提升”,那么算法标记被该赋值语句定义的变量x为“不可提升”;注意到,算法中使用映射Promote[e]来记录给定的表达式e是否可提升,特定的常量值⊥代表不可提升。若S为循环语句loop(x,e),其中x是循环遍历,e是循环体,则算法标记S的循环变量x为“不可提升”。对于语句S中那些没有被标记为“不可提升”的表达式e,都可认为是循环不变量,因此,算法生成一个新变量z,将S中的表达式e用变量z改写,并将识别的循环不变式的候选z←e添加到循环不变式集合R中供后续处理。
算法接着对循环不变式集合R中的每个循环不变式z←e进行分析。算法调用代价函数cost(e)计算外提表达式e的代价,当且仅当该代价大于等于给定的阈值K,并且表达式e没有副作用时,算法才真正将不变式z←e外提;否则,算法放弃对不变式z←e的外提尝试,并恢复被替换的表达式。代价常数K的取值与目标平台硬件和编译器密切相关,在通常情况下可取K为1。
LICM 算法的输入T是一棵树,设树中的语句节点和表达式节点数量为n,Normalize 函数时间复杂度和空间复杂度为O(n),具体分析在下节给出。LICM 算法在规范化之后,第一个循环遍历T中的语句节点,该循环内的第一个内层循环遍历语句节点内的表达式节点,并记录对合法的表达式的赋值语句,第二个内存循环处理记录的合法表达式的赋值,cost 函数的计算虽然是递归的,但是在计算过程中存储每个表达式对应代价值,因此每个表达式只会被计算一次,所有cost的执行时间和表达式节点数量线性相关。因此整个算法的时间复杂度和输入T中语句节点和表达式节点数量线性相关,LICM 算法的时间复杂度为O(n)。整个LICM 算法除T外所涉及的存储结构为R,Promote 和cost 记录表达式的代价值所需的存储。以上三个存储结构的任意一个的大小最多为表达式节点数量,因此空间复杂度为O(n)。Halide 编译器中的循环不变量外提算法也是在树结构的中间表示上进行,时间复杂度为O(n),空间复杂度为O(n)。本文算法的时间和空间复杂度都不差于Halide编译器的循环不变量外提算法。
传统编译器中的循环不变量外提算法,如LLVM中的外提算法,都是在基于基本块的流图上设计和实现的。这种实现方式主要的缺点是程序在下降的过程中丢失了如循环、作用域以及条件表达式等高层程序信息,因此在执行循环不变量外提算法前这些必要信息都要通过额外的操作来恢复。另外,在编译器低层次的中间表示中,表达式或语句的表示形式发生了改变,这导致原本在高级表示上显而易见的优化时机在后面的优化中很难被发现。而本算法充分利用了深度学习编译器的主要特点,面向其高级中间表示实现循环不变式外提,弥补了传统循环不变量外提算法的不足。另外,该算法和已有的类似循环不变式算法也很不相同,如本算法使用的新的前置处理方式对表达式做变换,而不仅仅是像Halide 那样只对加法减法表达式做重结合;这使得本算法对冗余消除得更为彻底,避免了需要对外提的不变量做公共子表达式消除的额外工作,让目标平台编译器更加简化。
3.3 规范化
规范化指的是通过对语句和表达式进行保语义的变换,使得变换后的程序更利于后续循环不变量外提,或目标平台编译器的优化。规范化最主要的操作包括:调整表达式中操作数的顺序和对条件表达式和分支的合并操作。调整操作数顺序是指利用特定的代数性质,如结合律、交换律和分配律等,对表达式进行重结合优化,将其划分成常数部分、循环不变部分和变量部分。尽管这本身并不能改进性能,但由于某个表达式的子表达式是否为循环不变表达式,很大程度上取决于操作数的运算顺序和结合关系[16],因此,调整表达式操作数顺序能够给循环不变式外提优化带来明显的提升效果。例如,假设下面给定的两个表达式中,只有i是循环迭代变量,j为外层循环的迭代变量:
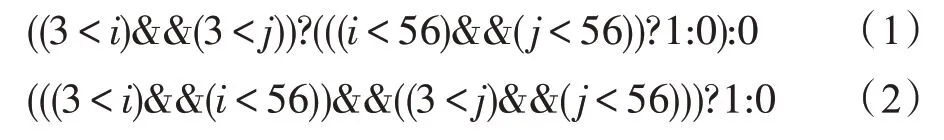
表达式(1)对应的抽象语法树如图2 所示,算法会计算得到两个候选的循环不变式:(3 <j)和(j<56)。而表达式(1)在规范化过程中,把(3 <j)和(j<56)放到了一起,得到表达式(2),其对应的抽象语法树如图3 所示,表达式顺序调整后的作用如下:变换之前的两个循环不变式(3 <j)和(j<56)在调整顺序后形成了新的循环不变式((3 <j)&&(j<56)),比原先的多外提了一个取并的运算操作。根据以上的观察,调整表达式的操作数结合顺序的思路为:对于某个满足结合律的运算,把操作数按照所包含循环迭代变量对应循环的嵌套深度,以递增或递减进行排序后结合到一起,这样的操作能够将分散的循环不变式结合到一起,利于循环不变量表达式的发现。基于以上特点,可按如下步骤把循环不变的表达式结合到一起:
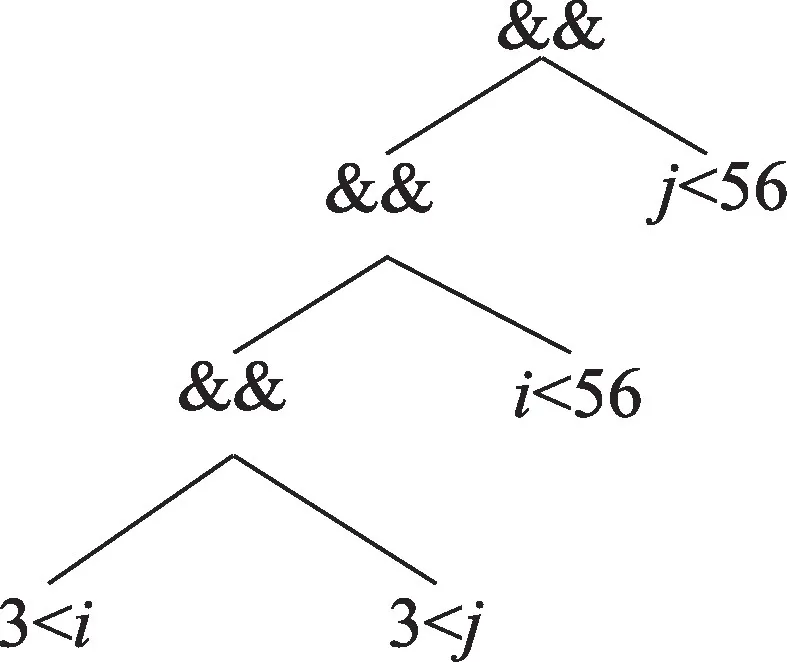
图2 表达式(1)的抽象语法树Fig.2 Abstract syntax tree of expression(1)
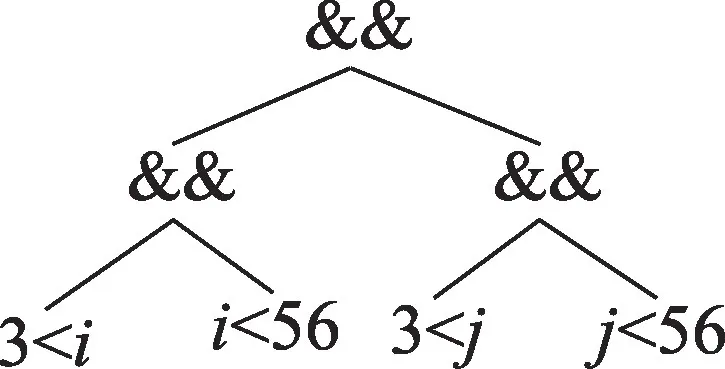
图3 表达式(2)的抽象语法树Fig.3 Abstract syntax tree of expression(2)
(1)为每一个表达式e绑定一个整数rank:
(2)若表达式e为常数,则为其绑定rank为0;
(3)若表达式e为循环迭代变量,则为其绑定rank为嵌套循环的深度,否则:
①绑定定义该变量的操作数的最大rank值。
②对于满足结合律的运算,按照rank值递增为每个表达式排序后,重新结合为新的表达式。
条件表达式对应判断条件的成立和不成立,都有对应的返回值,而在嵌套的条件表达式中,多个判断条件成立与否可能对应于同一个返回值,对此,可以合并这些具有相同返回值的判断条件,使得变换后的表达式中的循环不变量更完整。例如,假设下面的表达式中只有i是循环迭代变量:
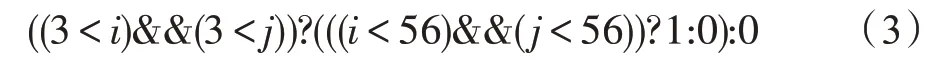
表达式(3)对应的语法树如图4 所示,算法确定的候选循环不变式为3 <j和j<56。表达式(3)经过化简后得到条件表达式:

图4 表达式(3)的抽象语法树Fig.4 Abstract syntax tree of expression(3)
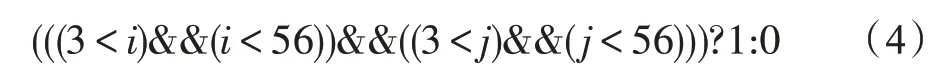
其对应的语法树如图5 所示,算法发现了更好的候选循环不变表达式((3 <j)&&(j<56)),并且((3 <i)&&(i<56))和((3 <j)&&(j<56))这两个表达式的形式更利于实现与布尔表达式相关的窥孔优化。最后,对于相邻的具有相同跳转条件的分支,算法可以合并这些分支语句。算法2 给出了规范化算法Normalize(T)的伪代码实现。

图5 表达式(4)的抽象语法树Fig.5 Abstract syntax tree of expression(4)
算法2表达式规范化算法

该算法接受原始程序T作为输入,并输出优化后的程序。算法遍历程序T中的表达式e,并根据表达式e的语法形式对其进行处理:如果表达式e为条件表达式if(e1,e2,e3),则算法调用函数condCollapse(e),对可以进行判断条件合并的表达式e进行优化,并返回优化后的结果。接下来,算法按照前面讨论的步骤,计算表达式e中的所有变量和子表达式的rank值。对于完成rank值计算的表达式e,算法遍历其所有满足结合律的操作符⊕,调用deconstruct(e,⊕)将由操作符⊕连接的子表达式转换为有序子表达式序列L;然后,算法调用函数stableSort(L)使用稳定排序算法将L按照rank值从小到大排序并返回排序后的序列L;最后,算法调用函数groupExpressions(L,⊕)将L中相同rank值的子表达式用操作符⊕连接为新的表达式并返回变换后的序列L,并调用函数construct(L,⊕)用操作符⊕依序将L中的所有子表达式连接,并返回变换后的最终结果e。算法对程序T中的所有表达式遍历结束后,调用函数ifconcat(T)合并T中相邻的具有相同分支条件的分支语句,并返回变换后的程序T。函数ifconcat(T)本质上完成控制流优化,通过对分支语句进行合并优化,可有效减少语句和表达式的数量,减少优化算法的执行时间。Normalize 算法的输入T是一棵树,设树中的语句节点和表达式的数量为n,外层循环遍历T中的表达式节点,condCollapse 所需时间和判断条件数量线性相关;loopDepth 函数递归求每个变量的嵌套深度,在递归过程中保存遇到的变量的嵌套深度,因此每个变量的深度只会被求一次,所需时间和表达式数量线性相关。最后一个内层循环对表达式重结合,deconstruct、groupExpressions 和construct 都是和表达式数量相关的线性时间;stableSort 排序算法根据rank值进行排序,因为每个表达式的rank值都是0 到嵌套深度之间的整数值,可以使用计数排序,该排序算法为线性时间复杂度,ifconcat 和T的语句数线性相关,因此Normalize 算法时间复杂度为O(n)。空间复杂度的分析和LICM 的思路相同,也为O(n)。
传统的标量编译器在进行循环不变式外提前,也都会执行代数化简和表达式重结合等优化遍,来完成前置的处理和准备工作。而在深度学习编译器中,和内存读写相关操作的优化应该在更加低级的中间表示上进行,代数化简和常量传播等优化由TVM 原生的simplify 优化遍完成,因此,规范化算法可以更专注于对下标和条件表达式进行特定变换,以有利于循环不变量外提优化和控制流优化的实现。
3.4 代价函数
代价函数cost(e)接受表达式e作为输入,计算并返回e的外提代价值。当且仅当该函数的返回值大于等于给定的阈值K时,编译器才认为有足够的收益,并将该表达式e进行外提。需要计算代价函数cost(e)的原因是TVM 生成的高层算子代码,还要经过目标平台编译器的编译,才能生成真正目标硬件上的可执行程序。由于目标平台编译器会在更低层次的中间表示上对程序做一系列优化,两个不同层次的优化之间可能产生矛盾,比如外提循环不变量和后端寄存器分配优化存在矛盾,当循环内的一条指令的执行需要一个不变表达式的执行结果时,有两种方法可以获取这个结果:(1)每次指令执行前重新计算;(2)将计算结果保存在变量中,每次指令执行前使用该变量。方法(1)中重复计算相同的表达式增加了冗余计算,但是减少了变量声明周期,降低了寄存器压力,利于有序寄存器分配优化。方法(2)消除了多次计算不变表达式的冗余计算,但是增加了变量生命周期,增加寄存器压力,可能导致后续寄存器分配优化效果下降。为了权衡消除冗余计算和寄存器分配优化之间的矛盾,避免两个不同层次的优化相互干扰,设计了一个代价函数cost(e)来计算表达式的代价,指导算法外提循环不变式。表达式代价值代表了计算表达式所需开销,也就是外提表达式的收益,因此仅当代价值大于某一阈值K时,算法才对该表达式做外提。对表达式e的代价函数cost(e)定义为:

当e是常数或变量时,其代价定义为0;当e是复合表达式时,其代价递归定义在其子表达式a上,另外加上其运算符⊕的代价。下面以一个具体的表达式x/1024+y为例,详细说明代价值的计算方式。根据定义有:

不同的运算⊕根据其需要的时钟周期的不同定义了不同的代价,其中加法指令需要的时钟周期较少,设置cost(+)=1,除法指令需要的时钟周期较多,设置cost(/)=3。因此有cost(x/1 024+y)=1+3+0+0+0=4。这个基础的代价函数cost(e)可以修改为适合于不同硬件平台的代价函数,例如,对于GPU 平台,其平台上的编译器NVCC 通常选择展开迭代范围很小的循环,并在此基础上执行其他的优化。因此,可以设置循环迭代范围很小的循环中的表达式代价值为0,避免两个不同层次的优化互相干扰。
4 实验结果与分析
4.1 研究问题
实验主要回答以下两个研究问题:
(1)性能。本文提出的新的循环不变式外提算法是否能够提升实际TVM 生成算子的性能?以及对哪些算子会造成一些特殊情况性能下降?如果有下降,原因是什么?
(2)正确性。本文算法改变了操作数的顺序,对于优化后生成的算子的正确性(即计算精度)是否会造成影响?
4.2 实验平台
实验使用英伟达的NVCC 编译器的10.0 版本作为GPU 平台的编译器。所有实验数据都在表1 所示配置的服务器上收集得到。

表1 实验环境Table 1 Setup of experiment
4.3 数据集
实验选择了TVM 的TOPI 算子库中的部分算子在不同输入规模下的实现,作为本次实验的基准测试集,本次测试涉及27 个算子和511 个测例。表2 列出了本次实现选择的所有算子及其测例数量。这些算子属于深度学习框架和TVM 常用的算子,并且实验对每一个算子都提供了大量在常见神经网络中不同输入规模的测例,在这些测例上的实验结果具有一定的代表性。

表2 算子测试集Table 2 Benchmark of operators
4.4 实验结果与分析
在研究算法对性能的影响时,为了减少实验误差,认为那些优化前后生成代码相同和运行时间小于50 μs 的测例为无效测例,且不考虑运行时间波动低于1%的测例。表2 给出了每个算子的有效测例数量,称有效测例数量大于0 的算子为有效算子。定义算子运行加速比S为:

其中,T0为原生TVM 生成算子的运行时间,T1为本次实验的原型系统生成算子的运行时间(即经循环不变式外提优化后算子运行时间)。定义算子平均加速比A为所有测例的加速比的算术平均值:

图6(a)给出了有效算子的平均加速比,图6(b)给出了有效算子运行时间加速比。图中的绿色虚线代表加速比为101%,橙色实线代表加速比为99%。从算子平均加速比的角度来看,相比原生TVM 编译得到的算子,本文算法编译得到的算子中有10 个算子性能得到了提升,占有效算子的47.6%,性能提升最明显的算子为conv3d_winograd,其加速比达到141.46%;只有1 个算子性能下降,占有效算子的4.7%,该性能下降的算子为conv2d_hwcn,其加速比为97.60%;其余算子性能不变。从算子总时间加速比的角度来看,相比原生TVM 编译得到的算子,本文算法编译得到的算子中有10 个算子性能得到了提升,占有效算子的47.6%,性能提升最明显的算子为conv3d_transpose_ncdhw,加速比为142.91%;只有1个算子性能下降,占有效算子的4.7%,该性能下降的算子为conv2d_hwcn,加速比为97.10%;其余算子性能不变。所有算子的总时间加速比为122.7%。对性能得到提升的测例,进一步分析了其优化前后生成的代码,发现表达式中的循环不变式被提出了循环外,分支和条件表达式也得到了相应的优化。首先,循环内的指令数目减少了,一部分循环不变的指令被移到了循环外;其次,计算谓词的指令得到了优化,一些有公共操作数的比较指令被减法或其他指令替换;再次,分支指令也用谓词执行来替换,减少了分支指令的数量;最后,因为循环内指令减少或者简化,nvcc 编译器对内层循环进行了更大范围的循环展开,同时其他的优化遍对展开后的循环体进行了更好的优化。对优化后性能下降的一个测例,进一步分析发现只有少量的简单表达式被提出了循环外,循环内的控制流结构和指令数基本没有发生变化,这些简单指令的延迟原本就会被流水线隐藏;另外,一些指令和同步指令的相对位置发生了变化,一些原本在同步指令后的计算被移动到了同步指令之前,可能改变后指令调度时的优化效果。需要特别注意的是,尽管这个特定算子的性能出现下降,但其2.9%的小幅下降仍然在可接受的范围内。

图6 算子加速比Fig.6 Operator speedups
另外,根据本算法对于不同类型的算子性能提升幅度不同,具体分析了本文循环不变式外提算法的使用场景。对于conv3d_winograd、conv3d_transpose_ncdhw 这类实现复杂的算子,经过前端调度优化后得到的中间表示包含大量的嵌套循环和嵌套条件表达式,本文算法对这类使用场景能够减少循环内的计算和分支,利于后端编译器优化的进行。在这类使用场景下本文算法能够起到显著的性能提升效果。对于像conv2d_hwcn、depthwise_conv2d_back_input 等这类算子代码中循环和条件表达式嵌套数较少,表达式形式较为简单,部分简单形式的冗余计算在底层编译器优化中也能被消除。且由于外提计算导致其中同步指令的相对位置发生变化,可能改变后续指令调度优化的效果。在这类使用场景下本文算法对于算子性能的提升可能得不到令人满意的效果。
为了进一步证明算法改进的有效性,选择Halide编译器的循环不变量外提优化与本文算法的优化效果进行比较,实验将Halide 编译器的循环不变量外提优化遍经过适配移植到了TVM 上。在原生优化遍的基础上,添加了对于条件表达式和其他符合运算结合律的运算的外提支持。实验结果如图7 所示,本次实验中最小的加速比为90%,因此将加速比减去89%后以2 为底取对数,以上操作是为了直观地对比两个算法的优劣,每个纵坐标计算方式为lb((s-89%)×100),其中,s表示算子加速比。红色的柱形表示Halide 编译器的循环不变量外提算法的优化效果。本次实验的有效算子测例中,忽略性能波动小于1%的测例。同时本文认为两个算法优化算子性能差异小于1%时为实验误差。实验结果显示,本文算法相比于另一比较算法,在5 个算子的性能提升效果上明显更优,占有效测试算子的23.81%;仅在1 个算子的性能提升效果上较差。其余71.42%的算子测例的性能提升效果差别不大。从优化效果明显提升的例子,如conv3d_transpose_ncdhw、depthwise_conv2d_back_weight 和conv3d_winograd 等复杂算子测例的生成代码中观察到,相比比较算法,本文算法在对于嵌套条件表达式、不变式的重结合方面表现都更好,外提了一部分没有被比较算法发现的不变式,减少了跳转指令数量。而观察性能下降的例子conv2d_hwcn,经过Halide 循环不变量外提算法优化后算子性能没有发生变化,而本算法的变化导致了性能的轻微下降,大约为2.9%。生成代码中控制流结构和指令数基本不变,但有一部分计算和同步指令的相对位置发生了变化,可能导致底层编译优化效果的下降。从总体效果来看,本文算法对算子性能提升效果明显优于比较算法,进一步证明了本文对于循环不变量外提算法改进的有效性。
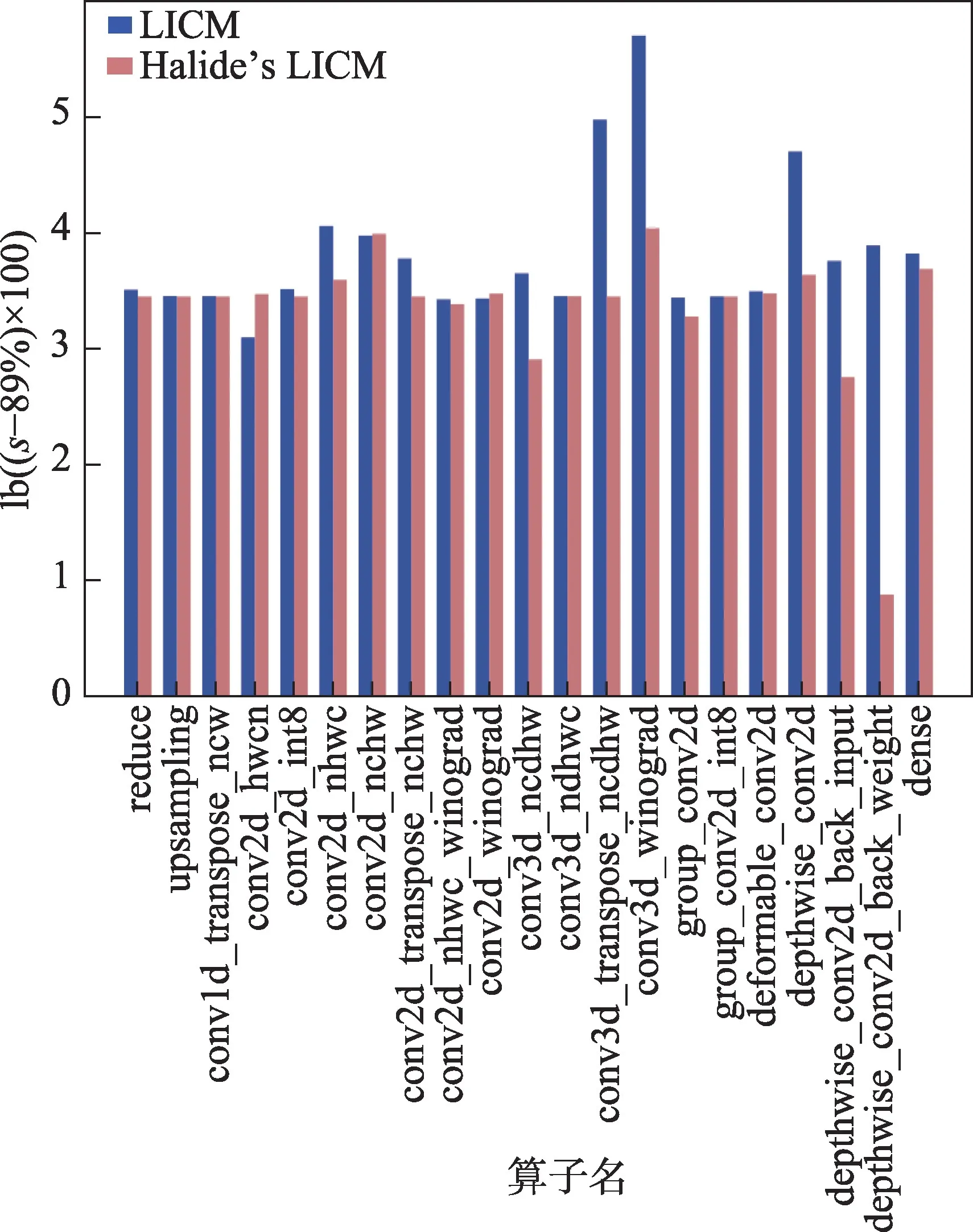
图7 本文算法与Halide编译器的LICM 算法对比Fig.7 Comparison between proposed algorithm and Halide’s LICM
本次实验研究的第二个问题为算子的准确性,算子的准确性主要由算子计算结果的精度来衡量。影响算子计算准确性的主要因素有硬件计算单元本身精度和数据计算顺序。硬件计算单元精度和实验硬件平台紧密相关,本次实验选择NVIDIA Tesla P4图形处理器。数据计算顺序主要依赖于前端的调度,另外优化遍对于中间表示的变换也会改变计算顺序,本文算法实现的优化遍只对于满足运算结合律的运算改变计算顺序,不会改变运算结果。为研究本文算法的正确性,对所有测例在GPU 上的运行结果与Python 实现的等价测例在CPU 上的运行结果进行了比较,由于浮点数的相等测试的约束,本实验设置误差容忍度为1E-5。实验结果表明100%的测例实验结果误差小于1E-5,这证实了本文算法的正确性。
4.5 结论
本文以TVM(0.7 版本)为基础,实现了添加循环不变式外提优化算法的原型系统,并在TVM 的TOPI算子测试集上针对27 个算子的511 个测例进行测试,并收集实验结果。对实验结果的分析表明,本文提出的循环不变式外提算法,弥补了闭源编译器NVCC在对复杂表达式的冗余删除和控制流优化存在的不足,完善了TVM 生成算子的优化过程,对算子性能提升产生了积极的作用。
5 结语
本文针对深度学习编译器,提出了一种新的循环不变式外提优化算法,并基于开源TVM 的0.7 版本实现了原型系统。对TVM 中的TOPI 算子库中的27个算子和511 个测例进行了实验,实验结果表明该新优化算法在保证正确性的情况下有效提升了算子性能。本文工作为TVM 或者其他深度学习编译器移植传统循环不变式外提算法提供了有益参考。

