面向动态路网的最优路径GCN 深度搜索方法
费 珂,秦小麟,迟贺宇,李 瑭
南京航空航天大学计算机科学与技术学院,南京211106
在路网中,最优路径以时间衡量,而交通情况受位置、时间、整体交通态势等影响动态变化,成为相关研究的难点。探索更高效、准确、实时的算法,在路网中进行最优路径的搜索规划,对更好地提供各类位置服务(location based services,LBS)具有重要的意义。
当前主流的定位技术有卫星定位和基站定位,前者包括全球定位系统、北斗等,后者包括射频识别技术(radio frequency identification,RFID)定位等。不同技术在各场景中表现各有优劣[1]:卫星定位的移动对象数据具有较强连续性,但易受高楼隧道等干扰,精度较低;基站定位如RFID 在基站密度较高的城市中,数据精确度较高、信息量大,但数据离散化、多冗余。近年来RFID 技术因其特有优势渐渐受到青睐,在各大城市逐渐普及。第五代通信技术、智能移动设备、定位技术的发展,使基于位置的社交、服务等随之兴起,推荐系统[2]、智慧城市[3]、智能交通[4]等领域都有了长足发展。
某交通局已部署大量RFID 私家车检测基站,覆盖城市交通的主体区域,应用于智能识别、流量监测、违规监控等方面。安装RFID 电子标签的车辆产生了海量移动对象数据,交通工作者当前重要任务之一就是从海量数据中挖掘有效信息,以优化各类位置服务。
在动态路网中搜索最优路径面临着许多难点:城市道路复杂,交通情况多变,海量的交通数据难免存在冗余、缺失等问题;现实场景中,城市内出行对路况尤为敏感,查询路径时当前、未来交通信息未知;路网内在模式具有时空相关性[5],理想的搜索依赖于对时间、空间信息的有效利用。
当前许多研究引入了启发算法、神经网络等,在不同场景都取得一定效果。启发式的蚁群算法搜索时通过迭代逼近最优解,可结合聚类及自适应机制等用于动态环境[6];部分神经网络方法如RNN(recurrent neural network)、LSTM(long short-term memory)等适合处理时序数据,学习出符合数据模式的模型[7],偏向于生成与历史轨迹相近的路线;强化学习通过智能体与环境交互获得处理未知场景的能力,使用奖赏函数寻求最大长期收益[8],结合深度学习框架来提升对各类信息的利用率以面对复杂场景。此外当前工作中还存在一些不足,例如忽视了现实场景中未来交通状况未知、需建模预测,而基于完全已知或随机的场景设计算法;此前基于机器学习的交通模型多使用卷积神经网络,因此无法直接用于图问题,需将地图网格化处理,在图结构与网格化的映射中存在失真。近年研究者提出了定义在图结构上的一系列图神经网络[9],如图卷积网络(graph convolutional networks,GCN)、时空图卷积网络(spatial-temporal graph convolutional networks,STGCN)[10]等,在交通、社交网络等领域表现良好[11]。
针对上述情况,本文提出了一种基于GCN 的动态路网最优路径深度搜索模型。模型使用图神经网络以避免网格化处理,挖掘时空数据、图蕴含的信息,同时利用历史交通数据对未来路网状况进行建模,使模型更贴近现实出行场景:基于RFID 数据集,将基站作为图节点、交通流量等信息作为节点属性,使用时空图卷积网络建模路网的动态变化;加深搜索深度,使用神经网络计算深度估价、搜索最优路径;最后在某交管局提供的RFID 数据集上进行测试。实验结果表明,该方法能够有效处理具有多维性和时效性的交通数据,整合路网中的时空语义信息并建模,通过深度搜索提高了最优路径查询的准确度。
1 相关工作
随着定位技术、时空数据库技术等各方面的发展,海量交通数据得以获取,关于路网中最优路径搜索问题的研究不断深入。动态路网中的最优路径搜索主要包含交通数据预处理、动态路网模型建立、动态图路径搜索等关键步骤。
路网中采集的数据信息,是典型的时空数据,具有维度高、语义复杂、时空动态关联的显著特征。对于RFID 交通数据,研究者很早就提出了借助数据库管理技术进行流处理[12]以及自适应清洁[13]的方法。近年研究者提出了基于动态标签、考虑数据冗余等改进方法[14],使得从庞杂数据中提取有效数据变得更加高效准确,适合后续的分析挖掘任务;针对交通轨迹数据中缺失、异常等数据缺陷,研究者提出了许多基于聚类、阈值划分的方法。刘云恒等人[15]在清洗策略引入了最大熵原理,适用于不确定RFID 数据流;Birant等人[16]在聚类算法上增加时间属性,提出了STDBSCAN(spatial-temporal density-based spatial clustering of applications with noise)算法处理时空数据;Cai 等人[17]使用数字孪生技术进行优化,使用改进的扫描线算法和F1 评估来确定阈值,更准确地发现数据缺陷。
目前,在交通领域研究者提出了大量机器学习模型,高效处理路网中相关问题。Zhang 等人[18]将时空处理单元引入残差神经网络,提出ST-ResNet模型,深度学习与时空数据的结合在行人流量预测等任务上表现卓越;Qiao 等人[19]将适合处理时序数据的LSTM模型应用于路网问题,预测短期交通流量;近年来图卷积网络因具有处理图结构与非欧氏空间数据的能力[20]备受关注,Yu 等人[21]设计基于图卷积网络的深度学习模型,高质量利用图中空间结构等信息,以时空卷积单元进一步学习移动对象轨迹的时序信息。
路网中的路径搜索问题,算法通常包含动态图的预处理和路径查询搜索两个主要步骤,研究者提出了不同处理方法。Wang 等人[22]基于图注意力网络,采用循环卷积网络与强化学习方法改进A*算法及其估价函数,得到基于历史数据的个性化路径。启发式的A*算法是一种求解最短路径最有效的直接搜索方法,Nannicini 等人证明了A*算法在动态图上的可行性[23],而Wang 的工作则证明了使用机器学习进行启发式搜索的有效性。此外,Demiryurek 等人[24]系统研究了传统最短路径算法在时变空间网络的适用性;Li等人[25]使用具有自波动性的脉冲耦合神经网络(pulse-coupled neural network,PCNN),自适应地学习路网中信息;Panov 等人[26]使用深度强化学习框架(deep reinforcement learning,DRL),以交互、奖赏函数机制学习地图模式进而寻找最优路径,可用于智能体路径规划、城市导航等领域;结合其他一些启发式算法如遗传算法、蚁群算法的改良与混合模型也在不同场景中获得了不错效果[27]。
2 问题定义与深度搜索模型
令抽象路网G=G(V,E,W)是无向全连通的动态图,其中V是图顶点的集合,E⊂V×V是边的集合,W是边权重矩阵。RFID 数据集T中的记录Ti(carID,vertex,time…)是某一时刻某一基站收集到的车辆信息,其中还包括环境等其他属性。车辆运动轨迹H={T1,T2,…,Th}是多个连续记录的序列化。文中关键符号及含义如表1 所示。
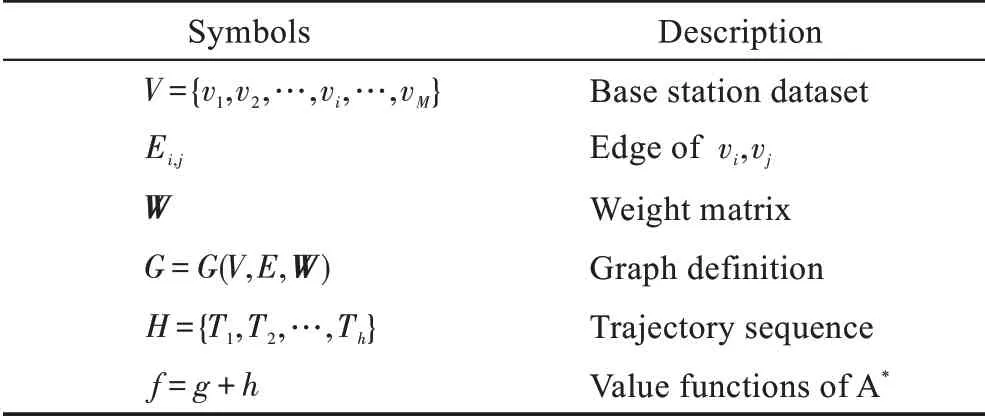
表1 关键符号及含义Table 1 Key symbols and their description
定义1(交通路网最优路径搜索)已知过去时间段t0至tl的路网G=G(V,E,W)的结构与信息,以及该段时间有效的车辆轨迹数据H={T1,T2,…,Th} 等信息。在未来的tl至tm时段,路网情况未知,给定出行的出发时间、起始点、终点三元组{n,n0,T},搜索拥有最小总时间代价的最优路径。
2.1 数据预处理
原始的RFID 数据以基站为主体,存储在时空数据库中,数据呈离散化,缺乏时空连续性,分布不均匀,因此需要进行预处理,转化为适当轨迹数据并进一步挖掘信息。
预处理过程包括:数据重组,由原始点数据集T计算出所有单次移动记录Hi(Ti,Ti+1);删除冗余数据与孤立数据,初步清洗数据;通过无监督方法,从大量数据中筛选出具有运动连续性的轨迹H={T1,T2,…,Th}。
不同任务对于轨迹数据具有不同程度的要求。位置预测问题要求数据具有时间的上下连续性;交通流量预测问题关注节点属性信息。在最优路径问题中,要求数据反映车辆的持续运动。两基站间的通行时间消耗受到时间、车型、周围路段情况等的影响。长时间跨度的数据中可能存在早出晚归、意外事故等情景,使得移动对象呈现“动-停-动”的运动状态,使得数据连接形成的轨迹不合理,进而影响对路网建模的准确度。因此,需要清洗数据使得轨迹H={T1,T2,…,Th}具有运动连续性。如图1 所示,将离散点连接为轨迹后,删除非连续运动状态的部分生成多段合理轨迹。

图1 划分轨迹数据Fig.1 Divide trajectory data
在RFID 原始数据得到的单次移动时间消耗中,异常值主要集中在非运动状态导致的过长时间消耗,数据整体上呈现半正态分布(half-normal distribution)。依照相同的起始、终止节点将初步筛选后的行驶记录划分为多个数据集合Ck,以广泛使用的K均值聚类算法检测异常数据,拉格朗日多项式插值对数据样本缺失时段进行填充[12]。数据预处理总体流程如算法1 所示。
算法1RFID 数据预处理算法
输入:原始数据集合T,顶点集合V。
输出:连续的运动轨迹H={T1,T2,…,Th}。
1.Tsorted←T//数据重排序
2.forTi,Ti+1inTsorteddo
3.drop isolated and redundantTi//删除孤立数据点、冗余数据等
4.Hi←Ti+1-Ti//计算单段移动轨迹
5.end for
6.Ck←divideHset//按顶点分类单段轨迹
7.for eachCkdo
8.thresholdck←Ck//计算阈值
9.drop out-of-range data//按阈值删除数据
10.ifHilacks data:
11.Hi←Interpolation(…Hi-1,Hi+1…)//插值法填充缺失数据
12.end for
13.H←∑Ck//整合轨迹
算法1 首先将原始RFID 数据集转换为移动记录并进行数据清洗、缺失数据填充,生成了具有运动连续性的轨迹H={T1,T2,…,Th},以提供更准确的交通信息,包括路网G=G(V,E,W)中不随时间变化的顶点邻接关系、顶点集V与权重矩阵W随时间变化的动态属性等。面对海量、高维、时空相关的交通数据,采用了低复杂度方法:对高维数据排序时由于需同时依照时间、地点等多维度信息,使用复杂度O(nlbn)的快排;排序后冗余与孤立数据清洗、轨迹计算、聚类及基于阈值的筛选清洗复杂度都为O(n);对缺失数据的填充复杂度O(n),且需要插值计算的缺失数据少,相对计算代价较低;因此数据预处理算法整体时间复杂度为O(nlbn)。通过数据预处理过程,有效解决了原始数据中的冗余、稀疏、缺失等问题,使数据可靠性更高。
2.2 动态路网建模
图卷积网络主要用来处理分类、预测等任务[18],针对路网最优路径搜索问题,将模型分为两大部分:对动态路网进行建模的STGCN 网络部分,使用以图卷积参数优化的深度估价网络函数的部分,整体模型如图2 所示。这一节将主要介绍对动态路网建模预测的STGCN 部分。
2.2.1 整体结构
记t时段交通路网为Gt=Gt(Vt,E,Wt),节点集Vt的空间属性不变,时间属性动态变化。STGCN 网络的任务是根据给定的t0至tl时段信息,建模tl至tm时段路网节点状况:

STGCN 模型中,使用空域卷积聚合邻接节点的空间信息,使用时域卷积传递输入序列的时序信息,使得网络处理具有时序特征的动态交通数据图的能力。经过时空卷积后节点特征将在时间、空间上聚合,如图3(a)所示。图3(b)展示了时空卷积模块(ST-conv Block)的结构,由两个时域卷积和一个空域卷积组成。依次进行时域、空域卷积计算。输入数据中,n为节点个数,Ci为特征通道数,网络输入M个时间步的数据序列X∈RM×n×Ci及对应的邻接矩阵。
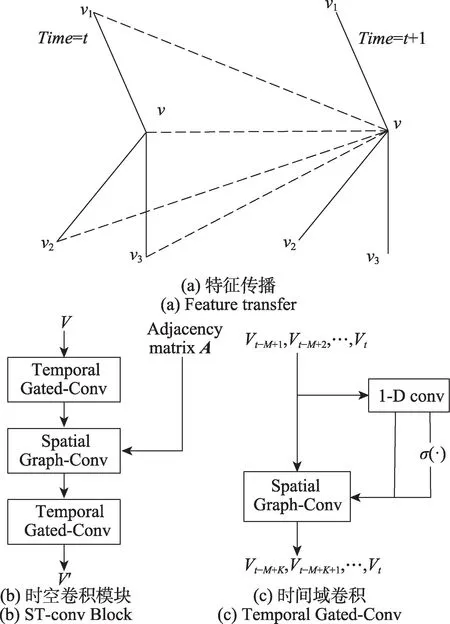
图3 特征传播与网络细节Fig.3 Feature transfer and network details
2.2.2 时间域卷积模块
该模块如图3(c)所示,属于一维时序卷积,由一维卷积和门控线性单元(gated linear unit,GLU)[28]构成。对于输入的特征,沿着时间维度进行一维卷积,计算后分为不经激活的P、使用Sigmoid 激活的Q两部分,作为门控单元的输入,再通过门单元GLU 进行权重筛选,整体时域卷积定义及计算过程如下:

式中,Γ是时域卷积核,*Γ是时域卷积操作;Wa和Wb为一维卷积核,*a和*b是卷积操作;⊙是按元素的Hadamard 乘积,σ(·)此处为Sigmoid 激活函数。一维卷积聚合时序上的前后信息,而引入门控单元GLU可以减轻梯度弥散,加速收敛,并使模型在深度增加时保留长期记忆(long-term memory),有利于深度网络建模。
2.2.3 空间域卷积模块
定义2(邻接域)定义相互可达的两个节点之间最小无权重距离记为邻接阶数、邻接距离,节点与自身邻接阶数为0。定义节点n的k阶邻接域:所有与n邻接距离小于等于k的节点组成的集合。
空间维度上的图卷积按提取特征方式分为两种:spatial domain,直接对邻接节点采样、聚合更新节点特征;spectral domain,通过傅里叶变换与拉普拉斯矩阵计算的频谱方法。Monti 提出了统一的框架,将两种方法概括到这个框架中[29]。STGCN 中空间域卷积为spectral domain,其卷积形式为:

图的度对角矩阵D和邻接矩阵A构成拉普拉斯矩阵L=D-A。式中U是拉普拉斯矩阵L的特征向量构建的矩阵,Λ是特征值构成的对角矩阵,gΘ(Λ)是卷积核,σ(·)是激活函数。
为了简化傅里叶变化的矩阵谱分解、矩阵特征向量计算等操作,降低计算量,模型使用Chebyshev多项式作为图卷积核。每层空域卷积有C0个卷积核Θ,Θ∈RK×Ci,输入特征向量X∈RM×n×Ci,计算公式为:

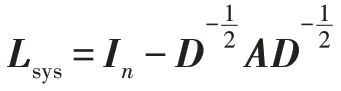
最后的输出模块包括一个时域卷积层和一个全连接层。全连接层有权重矩阵Z、偏置向量b,输出图中所有节点属性的估计值=Z(Γ*τX)+b。以估计值与真实值V的距离度量loss=||-V||2定义STGCN 的损失函数。
STGCN 交替使用时域卷积、空域卷积,使得不同时序的邻接信息向节点聚合。对动态路网进行建模时,每个节点的属性由过往各时段自身、K阶邻接域内所有邻接点的属性计算而来。相较于传统方法,时空信息的全面处理使得其能在动态路网的建模上取得更好效果。
2.3 深度搜索
启发式A*搜索算法广泛使用于路径搜索等任务,结合了最佳优先搜索和Dijkstra 算法的优点。其核心为估价函数:

式中,n为任意节点,g(n)是n与起始点之间的实际距离计算函数,h(n)是对n与目标点距离的评估函数。搜索路径时,A*算法维护两个集合:closed setC记录关闭节点,初始为空;open setO记录待拓展节点,初始仅包含源节点。通过最佳优先的方式进行拓展:

估价最优的节点next移动至C,其不在C中的邻接节点更新距离并添加至O。基于A*算法的启发式思想进一步优化,提升扩展时的搜索深度,使用深度估价神经网络替代人为设计的估价函数,以改进搜索效果。
2.3.1 深度搜索定义
在对动态路网建模后,路况虽然可以估算但仍存在误差,信息无法保证绝对准确。极小化极大搜索、蒙特卡洛树搜索等方法在信息不完全情况与博弈中,增加搜索深度可以有效改善搜索效果。在启发式搜索方法中,提高搜索深度,也有利于绕开路网中局部最优的节点,进而寻找最优的路径。
记n为待评估节点,其不在C中的邻接域节点集合为N,改进算法扩展节点时的评估方式,定义深度估价函数进行深度为2 的搜索,以加权形式得到的深度估价函数及扩展节点方式如下式:

式中,α为加权系数,f′(n)为深度估价函数。评估O中节点n时,需评估其邻域内其他节点:计算n与起始点之间的实际距离的g(n)不变,h′(n)则以邻域内节点估值的加权计算,从而定义n的深度2 估价f′(n),选取具有最小深度估价的节点进行拓展。深度搜索效果取决于深度估价函数的效果,除了加权计算外,也可以朴素地取邻域内节点的最小估价,或者使用机器学习方法进行估价计算。原始方法可视为深度1 搜索,在深度2 搜索的基础上进行推广,可以定义其他深度的搜索。
2.3.2 深度搜索复杂度
搜索深度的增加会对搜索的复杂度造成影响,需要确保其复杂度可控。
定理1(深度搜索复杂度约束)将一次A*算法搜索时访问过的节点记为集合A,A⊂V。设n为图节点数,k为节点度的最大值。当搜索深度增为1+h时,搜索计算的节点数小于k×(k-1)h-1×|A|。
证明记n0,0为某步深度搜索的开始节点,Ni为其i阶邻域,与n0,0邻接距离为i编号为j的节点为ni,j,节点的度记为d(n)。k为图节点度的最大值且k>2,k≤2 时图极简且不符合任务场景。以sum(h)表示n0,0深度1+h搜索所需访问计算节点的总次数,以s(h)表示第1+h深度搜索访问次数。由于路网的复杂性,ni,j节点在n0,0的i阶邻域首次出现后,仍存在被更长路径访问到并得到新的编号、剪枝保留最小代价路径的情形,不影响证明。
原始算法仅计算n0,0,搜索深度为2 时,访问并计算n0,0节点的d(n0,0) 个邻接节点n1,0,n1,1,…,n1,m;若n0,0非全局搜索的起始点则为d(n0,0)-1,排除其父节点。因此sum(1)≤k。


由A*算法性质,合理的启发式估价函数可以优化搜索过程,以最差情形作为搜索节点上限,深度搜索对每个节点进行深度1+h的搜索扩展,约束整体访问计算总节点次数|A′|:

不等式中supE为定义在实数域上的集合上确界,任意节点的sum(h)可由最差无剪枝情况的值进行缩放限定。综上,进行深度搜索扩展后,搜索计算节点次数小于k×(k-1)h-1×|A|。
定理1 定义于任意结构的图,对任意阶深度搜索的复杂度进行分析与约束。在理想的网格形交通路网中,节点度最大值k=4 且存在剪枝,除初始节点外每个节点有三个子节点,每个深度存留节点nh,j数量为4×h,此时sum(h)≤6×h×(h-1)+4,由定理1 中不等式|A′|≤sup{sum(h)|n∈A}×|A|,整体复杂度也大大降低。相较于定理1 中假设的任意图结构且无剪枝最差情形,现实路网与理想网格路网更为接近,结构稍复杂,原始算法的时间复杂度为O(|V|2),深度搜索算法的时间复杂度为O(k2h2|V|2),由于h、k是远小于|V|的常数,也可视其复杂度阶数未增加仍为O(|V|2)。
2.3.3 深度搜索方法
深度搜索方法效果取决于深度估价函数的准确性,设计了仅考虑最小值的深度估价方法、基于距离差的加权深度估价方法以及使用神经网络进行深度估价的方法。其中,仅考虑最小值的方法以待评估节点邻接域中的最小估价函数值作为深度估价;基于距离差的加权方法,以邻接域内节点与终点的距离计算加权系数α,使用归一化指数函数(Softmax)使得各权重占比更平滑,计算如下:
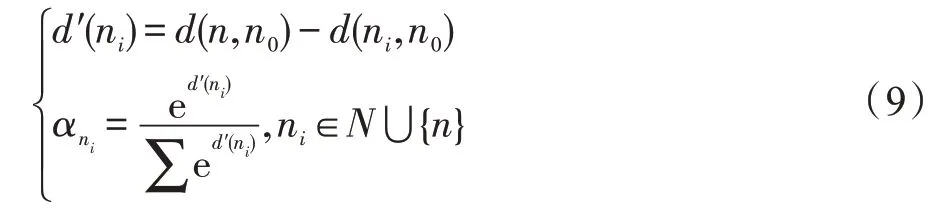
式中,n0为终点,d(n,n0) 为两节点的曼哈顿距离,d′(ni)为待评估节点n、节点ni距离终点的距离差,数值越小则距离越远,节点权重占比越低。
深度估价是对邻域节点信息的聚合与计算,因此可以使用深度估价神经网络替代人为设计的深度估价函数,通过训练学习深度估价,并结合图卷积单元权重系数进行优化。其结构如图2 右侧深度估价网络部分,计算公式如下:
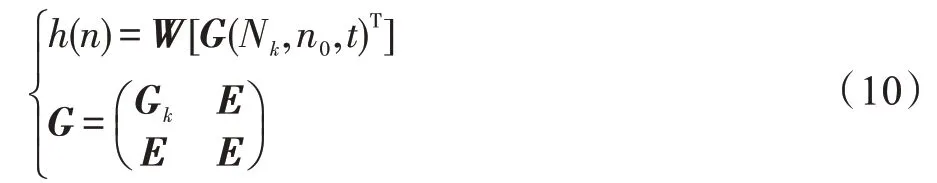
式中,G是全连接权重矩阵,其中Gk借助图卷积单元参数进行构造,K是邻接域阶数,E表示默认的随机参数构造;Nk由待评估节点K阶邻接域内节点构成,与终点n0、时间戳t一起作为网络输入;以W示意其他全连接层的计算。深度估价网络通过聚合邻接域内信息进行深度估价计算,同时关注了时间信息。最优路径深度搜索算法GCN-Search整体流程如下:
算法2最优路径深度搜索算法
输入:顶点属性序列{V0,V1,…,Vl},邻接矩阵A,查询起点、终点、时间三元组{n,n0,T},T>t。
输出:路网中最优路径{n,v1,v2,…,n0}。
1.Input {V0,V1,…,Vl}//由算法1 获得输入序列
2.divide {V0,V1,…,Vl} to train &validation set//将数据划分为训练集与验证集
3.Put train set into STGCN//输入训练集
4.forepochinepochsdo:
5.Calculate prediction andloss//通过模型计算结果与损失函数
6.Adjust STGCN parameters//反向传播调整网络参数
7.early stopping//在验证集使用早停法
8.end for
9.{Vt+1,Vt+2,…,Vm}←STGCN({V0,V1,…,Vl})//未来路网建模
10.train setH←{Vt+1,Vt+2,…,Vm}//生成训练集
11.as step 4~7,train Deep Valuation Network withH//训练深度估价网络
12.whilen0not in closed setC://深度搜索
13.n∈O,f(n)←GCN//计算深度评估值
14.updateCandO//更新状态集
15.end while
16.output the path of query{n,n0,T}
在算法2 中,依次利用训练集数据训练了建模路网的STGCN、深度估价网络,关注了空间信息与时间信息的利用,通过深度搜索给出查询{n,n0,T}的解。其中,STGCN 网络需要使用路网中所有节点信息对路网进行完整、准确的建模,深度估价网络则使用邻域内相关节点进行计算,将模型分为两个网络部分,可使得计算操作更灵活简便。
3 实验与分析
3.1 数据集与实验环境
为验证模型性能效果,在某交管局提供的RFID车辆数据集上进行测试。原始数据集包含548 个基站地理位置信息、基站记录的通过车辆信息,时间跨度2014 年9 月1 日0 时到9 月30 日24 时,包含近百万车辆,数据特征包括通过时间、基站编号、车牌号、车型等。本文主要关注其中的时间位置信息,对数据进行抽象简化、轨迹化等预处理,并构成属性以5 min为间隔动态变化的抽象路网,包含10 个节点的中短距离路径查询,作为实验数据集。
模型基于Pytorch 深度学习框架,实验的运行环境为:ubuntu16.04(64 bit),Intel Xeon E5-2609 CPU,16 GB RAM,NVIDIA Tesla K40m GPU。
3.2 路网建模效果及深度搜索方法比较
最优路径深度搜索算法经由STGCN 得到对路网建模的中间结果,在中间结果的基础上进行深度搜索。完整算法由两部分共同组成,针对这两部分进行独立的实验比较。
3.2.1 不同参数对STGCN 建模效果的影响
对于路网建模结果的优劣,用节点属性的估计值y~ 与真实值y之间的均方根误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)等指标进行评价,三者从不同角度反映估计值与真实值之间的误差,误差越小则表示建模结果越精确。网络的损失函数loss=||V^ -V||2与误差指标的变化趋势总体上一致。
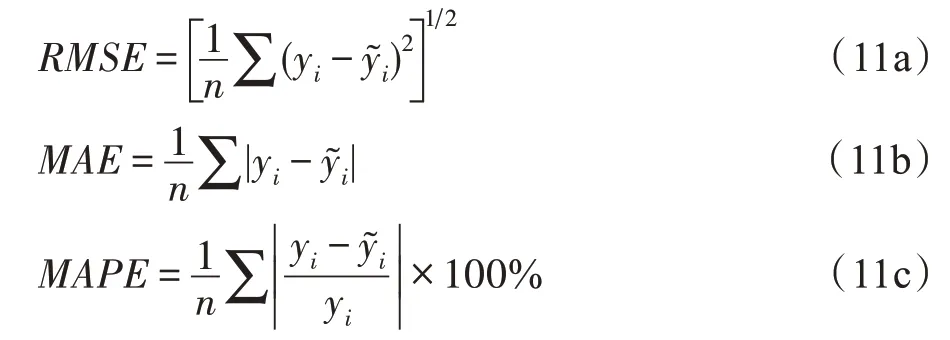
STGCN 的训练中,循环中的一个epoch指完整的数据集在网络上进行一次完整计算,所有训练样本进行正向计算得到损失函数值loss并反向传播调整网络参数。为了挖掘数据间的模式,往往需要循环多次,并在每个epoch打乱数据顺序消除数据间的相关性,提高模型泛化能力。同时,在训练集上迭代次数过多可能造成过拟合的情况,GLU 单元、dropout方法可以在一定程度上避免过拟合。
图4 展示了STGCN 部分预测近期路网状况的损失函数变化情况。损失函数值随着epoch增加变化:在训练集上,迭代过程中损失函数值稳定下降;在验证集上,损失函数值先呈现振荡下降,逐渐趋向平稳,在最后阶段损失函数值略上涨呈现轻微过拟合。为了保证模型预测的准确度与泛化能力,并尽可能避免过拟合状况,最终选取epoch参数为30 进行训练,并采用early stopping 方法,当模型在验证集上的表现变差时停止训练。
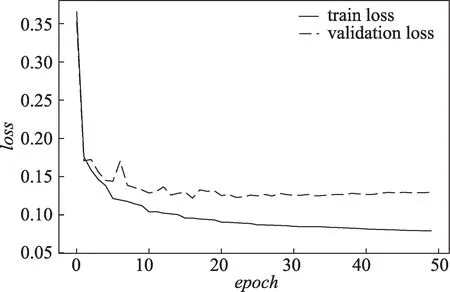
图4 训练集、验证集损失函数变化Fig.4 loss on train set and validation set
训练中,内存限制使得数据无法一次性载入,而是分批次投入训练。批次大小batch_size影响着模型效果,过小时收敛效果较差,适当增大可以使得梯度下降方向更准确,但过大会导致模型收敛速度缓慢。
图5 展示了epoch=30 时不同batch_size对预测结果的影响。随着样本批增大,固定的训练轮次数下各项误差指标数值上升,取值64 时表现相对最佳。最终超参数epoch、batch_size的值选取30、64 进行训练测试,保证路网建模的准确性。

图5 批次大小的影响Fig.5 Influence of batch size
3.2.2 深度搜索方法效果比较
对于给定查询三元组{n,n0,T},有实际最优路径H,搜索算法得到含冗余的过程集A、预测路径H′,相关研究中路径的准确率P(precision)、召回率R(recall)可定义为:
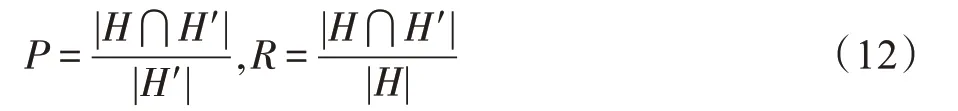
准确率P反映预测的路径与实际路径的吻合程度,召回率R反映最优路径的查全比例,路径中节点数相近使两者数值上趋于接近。此外,为查找最优解,启发式的算法在搜索过程中都拓展了大量冗余节点即A,可以使用|H′|/|A|反映搜索的有效率。
2.3 节定义了三种深度估价及搜索方法,仅最小值深度估价的搜索(only-min)、以距离差加权深度估价的搜索(dis-α)、基于深度估价网络的搜索(GCNSearch),并与A*算法进行对比。深度搜索方法效果的实验与建模部分相互独立,在信息已知的交通图上进行。图6展示了几种深度方法搜索过程的有效率。

图6 不同估价方法的结果Fig.6 Results of different valuation algorithms
实验对比可知,采用深度估价的方法相比A*方法搜索有效率更高。这说明了使用深度估价方法可以有效提高估价函数准确性,改善搜索效果。其中,仅最小值深度估价方法在复杂路网任务中表现略好于更精细的距离差加权方法,基于图卷积核参数的网络GCN-Search 表现最佳。整合两部分得到调参后效果最佳的路网最优路径深度搜索方法GCN-Search。
3.3 不同算法对比分析
针对定义1 的城市出行情景,将贪心策略搜索greedy、神经网络PCNN[25]以及深度强化学习方法DRL[26],与本文深度搜索模型GCN-Search 进行对比。该情景中进行最优路径搜索时,当前与未来的路网信息是未知量,各模型得到近似最优解的预测路径H′,图7 展示了几种算法的准确率、召回率、平均查询时间。从图中可以看到,GCN-Search 的准确率、召回率均高于其他算法。相较于效果较好的深度强化学习方法,准确率、召回率分别提高了0.044 2、0.079 1。查询时依赖大量矩阵运算与路网更新,使机器学习方法平均查询时间都较高;因仅使用邻域内相关节点及时间位置信息进行计算,GCN-Search 深度搜索的时间消耗略低于计算路网整体的DRL方法。

图7 不同算法模型结果比较Fig.7 Results of different algorithms
实验表明GCN-Search 在城市出行场景中,能有效利用动态路网中的时空信息,学习路网内在模式,对路网进行合理建模并准确地对节点进行估价,从而找到更接近最优的路径。绝对数值上,所有算法效果都并非极佳,一个原因是动态的现实路网存在代价相似的多条路径,算法得到的结果陷入其中从而与最优解有一定差距。
4 结束语
动态路网中的最优路径规划是计算机和交通方向的研究热点,可为各类基于位置的服务和应用提供重要支持。本文考虑到在动态路网场景中,充分利用时间、空间信息可以改善最优路径搜索效果,使用STGCN 的建模、加深搜索深度的实验结果证明了这一思想的可行性。同时相较于以往方法,本文将最优路径搜索问题定义在路网未来状况未知需建模预测的情景中,更接近现实出行情况,以图卷积网络建模路网动态变化,使用深度估价网络替代人工设计的估价函数,获得了理想的实验结果,具有一定实用价值,也体现了图神经网络、启发式思想解决交通领域问题的强大能力。但是,该算法对RFID 数据的高维度信息利用率较低,接下来将重点关注如何利用多维语义信息使路网建模与现实更吻合,进一步提高效果。

