大面积超薄蒸汽腔力学特性仿真分析
聂晓展,程 鑫,王珊珊,李春煜,杨 光*,吴静怡
(1.上海交通大学制冷与低温工程研究所,上海 200240;2.上海卫星装备研究所,上海 200240)
如今,随着电子技术的快速发展,电子设备中元件的集成度越来越高,使得设备的单位面积发热功率逐渐增大。研究表明,电子器件表面的平均热流密度已达到100 W/cm2以上,局部表面的热流密度更高[1]。发热功率的增大将导致电子器件工作温度显著提高,而工作温度过高是电子器件失效的最主要原因之一,其失效率随着工作温度的升高呈指数增长趋势[2]。因此,为保证电子器件高效、稳定地运行,必须利用有效的散热技术防止过高的工作温度。解决高热流密度散热的首要问题便是如何把集中的热源快速扩展至大面积表面进行冷却[3]。
在平板热管的基础上,可实现高效径向热扩散的蒸汽腔逐渐被广泛关注,其工作原理为:热源与蒸汽腔的蒸发侧直接接触,蒸发侧毛细芯内的液体工质吸收热源输入热量蒸发形成蒸汽,压差驱动蒸汽在空腔内迅速扩散,并在另一端冷凝侧释放潜热后凝结成液体。冷凝过程中释放的热量可由外部冷却如自然对流或辐射换热带走。冷却下来的液体工质沿着内腔吸液芯和支撑柱表面的毛细结构回流到被加热区,从而形成工作循环。因此,良好的温度均匀性、高效的热扩散能力是蒸汽腔的显著优势,这为解决航空航天一些高功率电子、光电器件的迫切散热需求提供了一种具有前景且有效的解决方案[4]。
目前对蒸汽腔的研究主要集中于优化蒸汽腔内毛细结构,提高液体输运效率。Ranjan 等人[5]对毛细芯结构中薄膜蒸发的微尺度模型进行了研究,分别对4种不同几何形状的毛细芯进行了建模,并对其蒸发性能进行了比较。Lurie 等人[6]对蒸汽腔内烧结芯体最佳几何形状的拓扑优化方法进行了数值模拟研究,研究表明采用最佳形状的毛细芯可提高蒸汽腔的运行性能,最大可将其传热能力提高到具有恒定厚度毛细芯的蒸汽腔的两倍。Peng等人[7]提出并研究了生物形态叶形结构毛细芯;Hwang等人[8]研发了多动脉蒸汽腔。结果均表明,使用上述特殊几何形状的毛细芯降低了毛细芯对水的阻力,从而可以向蒸发器区域提供更快速的液体回流。
除毛细结构以外,蒸汽腔中另一关键结构是支撑柱。蒸汽腔中的支撑柱主要起到承力以及增加额外的液体回流通道2 个方面的作用[9]。针对蒸汽腔内的支撑柱,大多研究的关注点是支撑柱作为液体回流通道时对蒸汽腔总体传热性能的影响。Min等人[10]研究了直径为5 cm 的圆形蒸汽腔,通过理论推导发现,随着蒸汽腔内支撑柱半径的减小,蒸汽腔总热阻也会下降,但是由于支撑柱表面的微结构需要提供足够的毛细力来防止液体阻塞,故支撑柱的半径存在一个最小值。Hwang 等人[11]通过实验发现,相比于无支撑柱的蒸汽腔,多支撑柱蒸汽腔具备明显的低热阻、高热流密度的特点。Hsieh 等人[12]通过分离变量,给出了有无支撑柱情况下,腔体内温度分布的三维解析解,并从蒸汽扩散阻力角度,考察了2 种情况下,蒸汽腔的传热性能变化。
随着航天技术的发展,电子元件尺寸和功率的增大导致蒸汽腔散热面积的增大,而外界环境的真空和较高的散热元件温度,会使大面积蒸汽腔产生相比于在地面工作条件下更大的内外压差和变形。所以,保证蒸汽腔整体的力学性能尤为重要。目前,与蒸汽腔力学性能相关的定量规律仍不明确。因此,本文将从腔体结构出发,通过各结构参数对腔体最大应力的影响,探究腔体各结构参数对其力学性能的影响规律。
1 研究方法及理论依据
大面积超薄蒸汽腔的散热面积可达1 平方米以上,而厚度仅为几毫米,内部支撑柱呈规律性周期分布。如果采用整体建模,将导致计算量过大,并且由于蒸汽腔在水平厚度方向和垂直厚度方向上尺度的差异,网格很难捕捉微观特性,从而不能保证仿真精度,故采用局部建模的方法,通过局部性能预测整体性能。在力学中,针对这种宏观尺度较大且微观结构具备周期对称性的研究对象,通常采用代表体元法(Represents volume element method,RVE)。
1.1 代表体元法
代表体元法通过分析结构微观尺度的力学性能,预测宏观尺度下结构的力学性能,可以在保证计算精度的前提下,快速建立有限元分析模型,减少计算时间[13-14]。代表体元法是基于整体结构渐进均匀化以及周期性边界条件的前提下提出的。随着单位面积支撑柱数量的增多,支撑柱间距变小,腔体内不同位置支撑柱的应力分布趋于一致。此时,研究单个支撑柱的应力分布等效于蒸汽腔所有支撑柱的应力分布。图1(a)为代表单元示意图,其中d为支撑柱直径,h为底板板厚,图中A1为支撑柱横截面积,A2为正六边形总面积,(A2-A1)/A2为孔隙率,取为ε。在图1(b)中,分别进行了蒸汽腔的整体建模和局部建模。对比两者可发现,其应力分布一致,并且最大应力仅相差8%。

图1 不同建模方法的对比Fig.1 Comparison of different modelling methods
1.2 力学建模基础
在弹性力学中,当薄板受到一般载荷时,总可以把每一个载荷分解为2 个分载荷,一个是作用在薄板中面之内的所谓纵向载荷,另一个是垂直于中面的所谓横向载荷[15]。显然该模型所受载荷为横向载荷,它们所引起的应力,形变和位移可以按薄板弯曲问题求解。
对于正n边形薄板的小挠度弯曲,当n无限大时,模型趋近于圆形薄板,所以可以参考圆形薄板的轴对称弯曲。
极坐标下弹性曲面微分方程为
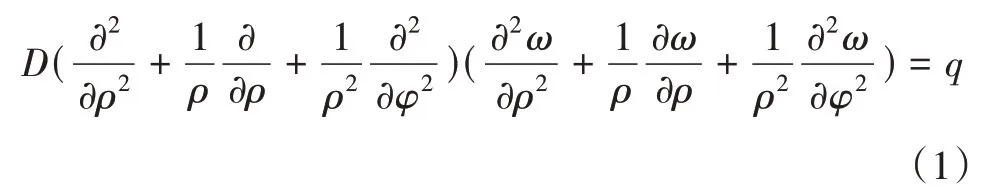
当横向荷载q=q(ρ),挠度ω=ω(ρ)时,式(1)可简化为
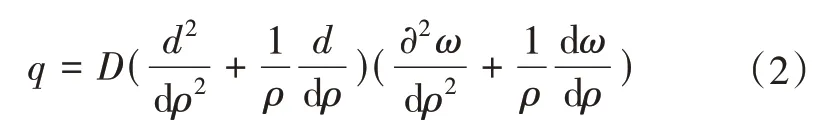
对式(2)积分4 次,便得到轴对称弯曲问题的挠度解答,即
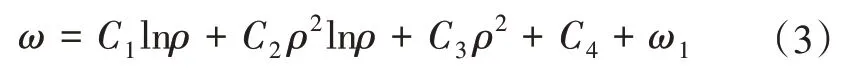
对于受均布荷载q=q0的薄板,特解
代入边界条件可解得C1、C2、C3、C4,进而得到ω的表达式。
极坐标下薄板内力公式为
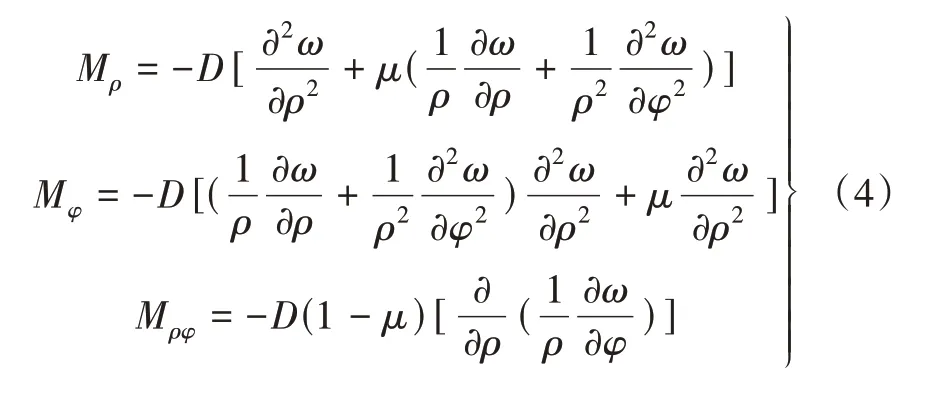
对于任意一点应力,有
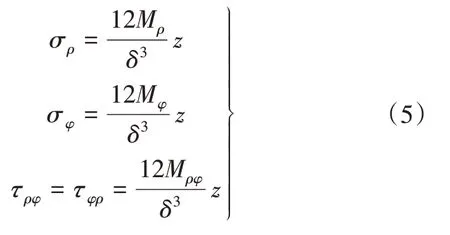
通过以上分析,对于周边固定圆形薄板受均布荷载q0的情况,应力情况为
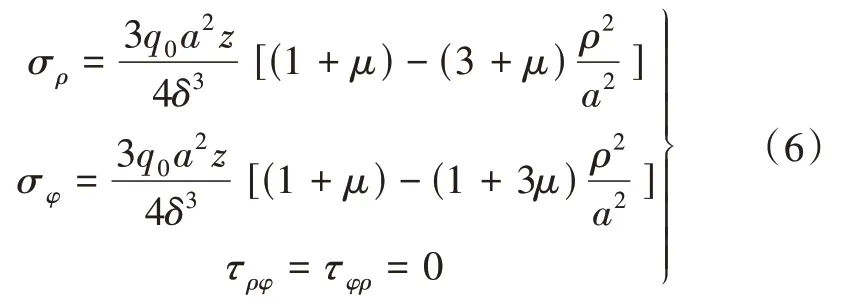
其中,a为圆形薄板的半径,δ为板厚,μ为材料的泊松系数。
1.3 有限元仿真方法
有限元仿真是力学分析中的常用方法。对于代表单元仿真模型(图1(a)),设置正六边形周边边界和支撑柱上表面为对称边界条件,上板面施加均布荷载q0=8 MPa,由于支撑柱与板面连接处会产生应力集中,在连接处设置1 mm 的对称倒角。材料为6061 铝合金。采用控制变量的方法,分别选取不同的支撑柱直径d、孔隙率ε、板厚h和均布荷载q0,依次判断各变量对单元体最大应力σMAX的影响。
由于本文代表单元模型结构的特殊性,无法通过解析解进行仿真精度校验,故需建立合理的验证模型。正n边形与圆形有一定相似性,且n越大,相似性越高;代表单元模型中支撑柱与底部薄板接触位置的应力集中是使该模型无法得到精确解析解的主要因素,考虑支撑柱直径为0 的极限情况。此时验证模型为圆形薄板的轴对称弯曲,可以由式(6)得到精确的解析解。
验证模型取半径15 mm、厚度2 mm 的圆形薄板,对薄板周边施加固定约束,薄板上表面施加1 MPa 均布荷载,材料为6061 铝合金。通过Ansys 有限元仿真软件,求得验证模型中心位置应力大小为26.86 MPa。相同条件下式(6)求得的解析解为30.23 MPa,仿真误差为11%,具备一定的仿真精度。
2 实验结果与讨论
对于大面积蒸汽腔结构稳定性问题,主要需要考虑在腔体最大应力位置不发生损坏或断裂,即保证腔体应力不超过腔体材料的屈服应力。本节将通过有限元仿真探究代表单元中各参数对蒸汽腔体最大应力的影响,并得到腔体最大应力随各参数变化的函数关系。
已知轴对称圆形薄板的应力分布与本文代表单元模型应力分布相似,由式(6)可知圆形薄板的最大应力在ρ=0,z=h/2处取得,有

其中,a2=S圆形/π,故有
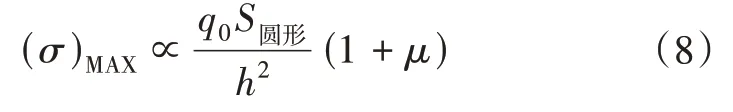
可见当其他条件一定仅改变圆板半径时,其最大应力正比于薄板的受力面积。代表单元模型最大应力表达式应与式(8)一致,其受力面积为

代入式(8)有

式(10)可表征代表单元中各参数对结构最大应力的影响趋势,通过下文的仿真数据可以确定各参数与最大应力之间准确的函数关系和具体的系数大小。
2.1 支撑柱直径对单元体最大应力的影响
如图2(a)所示,当固定板厚时,相同柱直径下,孔隙率越大,最大应力越大;相同孔隙率下,结构的最大应力随着支撑柱直径的增大而增大;不同孔隙率下,拟合函数中柱直径前的比例系数不同但指数项相同,都为2.1,说明比例系数与孔隙率有关,指数项与孔隙率无关。如图2(b)所示,当固定孔隙率时,相同柱直径下,板厚越大,最大应力越小;相同板厚下,结构的最大应力随着支撑柱直径的增大而增大;且不同板厚下,拟合函数中柱直径的指数项相同,都为2.1,故板厚只影响直径项前的比例系数,与指数项无关。
由图2可知,仿真结果中柱直径对最大应力的影响趋势与式(10)相一致。代表单元模型中支撑柱直径对结构最大应力的影响符合如下表达式:
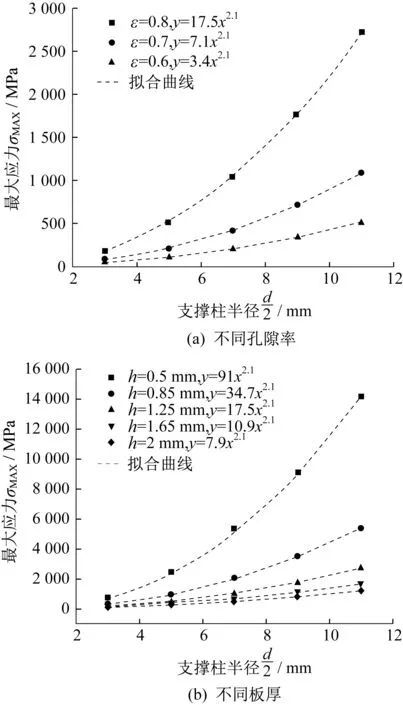
图2 柱直径对最大应力的影响Fig.2 Influence of column diameter on the maximum stress

其中,k1为待定系数,包含孔隙率和板厚的影响,而直径的指数项为固定值2.1,作为式(10)中直径指数项的修正。
2.2 孔隙率对单元体最大应力的影响
由式(10)可知,孔隙率对最大应力影响的形式应为无量纲ε/(1 -ε),以ε/(1 -ε)为横坐标,最大应力为纵坐标,在不同支撑柱直径和板厚条件下得到仿真结果,如图3所示。
如图3(a)所示,当固定板厚时,相同孔隙率下,最大应力随着支撑柱直径的增大而增大;相同柱直径下,最大应力随着孔隙率的增大而增大;不同柱直径只影响ε/(1 -ε)的比例系数,对其指数项无影响。如图3(b)所示,当固定柱直径时,相同孔隙率下,最大应力随着板厚的增大而减小;相同板厚下,最大应力随着孔隙率的增大而增大;不同的板厚同样只影响ε/(1 -ε)的比例系数,指数项与图3(a)中一致,都为1.534。因此,孔隙率对最大应力的关系式为
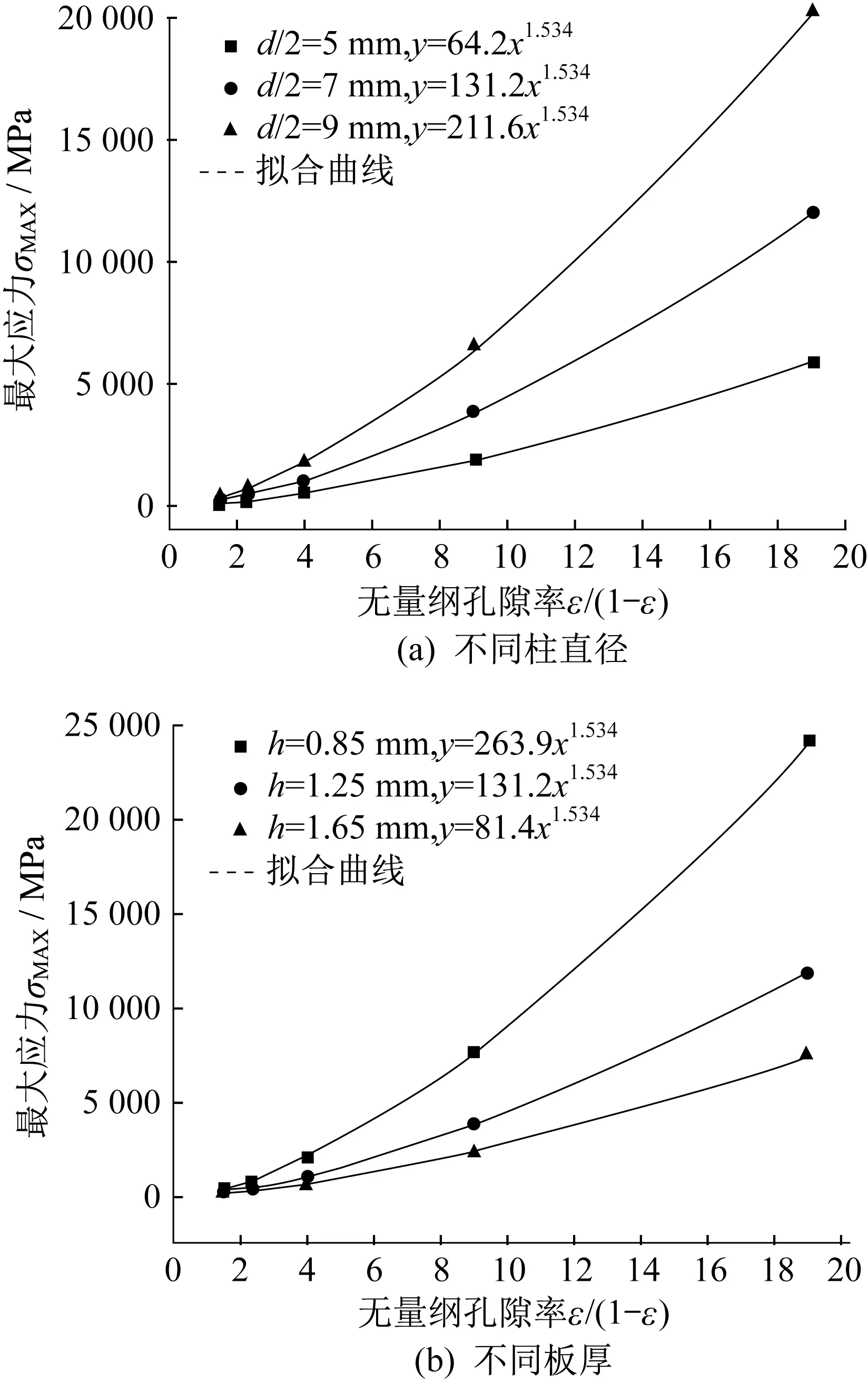
图3 孔隙率对最大应力的影响Fig.3 Influence of porosity on the maximum stress

其中,k2受板厚和支撑柱直径大小的影响,可以发现式(12)中孔隙率对最大应力的影响规律与式(10)相吻合,其中指数项1.534 为式(10)中相应ε/(1 -ε)指数项的修正值。
2.3 板厚对单元体最大应力的影响
如图4(a)所示,当固定支撑柱直径时,相同板厚下,最大应力随着孔隙率的增大而增大;相同孔隙率下,最大应力随着板厚的增加而减小;不同的孔隙率只影响拟合函数中的比例系数和常数项,对板厚的指数项无影响。由图4(b)可知,当固定孔隙率时,相同板厚下,最大应力随着柱直径的增大而增大;相同支撑柱直径下,最大应力随着板厚的增加而减小;不同的柱直径下板厚的指数项相同。可以发现板厚与最大应力呈负相关,与式(10)相一致,当改变孔隙率和柱直径时,板厚的指数项皆为-1.94,故板厚与最大应力的函数关系可表示为
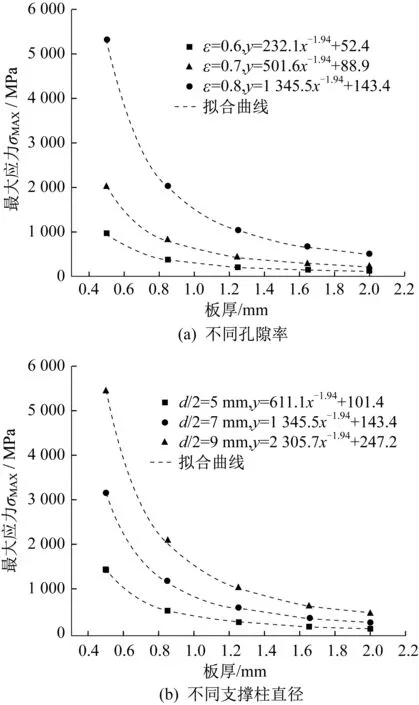
图4 板厚对最大应力的影响Fig.4 Influence of plate thickness on the maximum stress
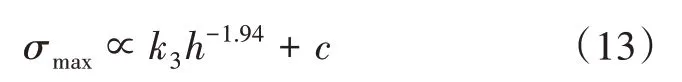
其中,k3、c与孔隙率和支撑柱直径有关,指数项-1.94为式(10)中板厚指数项的修正值。
2.4 腔体内外压差对单元体最大应力的影响
由式(10)可知,当单元体结构确定时,腔体内外压差与单元体的最大应力呈正比例关系,最大应力随着内外压差的增大而增大。若某一单元体结构在腔体内外压差p0=8MPa 时最大应力为σ0,则通过图5可知,同一结构不同压力p0下的最大应力σmax为

图5 腔体内外压差对最大应力的影响Fig.5 Effect of differential pressure on the maximum stress

2.5 最大应力关联式
在上文中,分别讨论了代表单元中的3 个结构参数以及腔体内外压差如何分别影响最大应力,确定了各自与最大应力的函数关系式。采用分离变量的方法,对上述式(11)-(14)进行拟合,可得如下函数拟合结果:
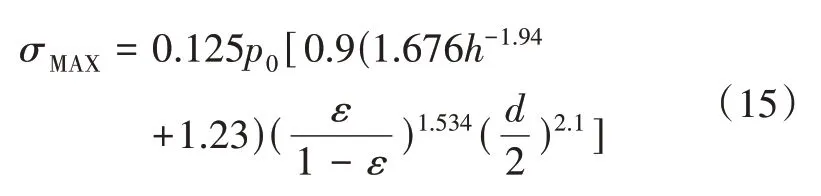
其中,σmax为蒸汽腔最大应力(MPa)、h为蒸汽腔上下板厚(mm)、ε为孔隙率、d为支撑柱直径(mm)、p0为腔体内外压差(MPa)。
同时对拟合所产生的误差进行了预估。对于大多数合金或纯金属,它们的屈服应力都在1000 MPa 以内,故选取了1000 MPa 以内的仿真值,将其与相同参数条件下的拟合函数所求值进行了比较,两者平均相对误差为13%,证明拟合函数具备一定的拟合精度。
3 结 论
我国航天技术的发展对大面积超薄蒸汽腔的力学性能提出了更高的要求。本文借助有限元仿真和代表体元法,分别对影响蒸汽腔力学性能的结构参数进行了研究。通过仿真计算,确定了各参数与腔体最大应力的具体函数关系。结果表明,蒸汽腔最大应力受蒸汽腔上下板板厚、孔隙率、支撑柱直径、腔体内外压差等因素共同影响。
(1)当孔隙率和板厚一定时,支撑柱直径与腔体最大应力呈正相关,即最大应力随着支撑柱直径的增大而增大,其影响规律近似于二次函数。进一步确定支撑柱直径的指数项为2.1,比例系数与孔隙率和板厚有关。
(2)当支撑柱直径和板厚一定时,最大应力随着孔隙率的增大而增大,且孔隙率以无量纲ε/(1-ε)的形式对最大应力产生影响,无量纲ε/(1-ε)的指数项为1.534,比例系数与支撑柱直径和板厚有关。
(3)当支撑柱直径和孔隙率一定时,板厚与腔体最大应力呈负相关,即最大应力随着板厚的增大而减小,板厚指数项为-1.94,其比例系数与常数项均与支撑柱直径和孔隙率有关。
(4)当蒸汽腔结构确定时,腔体的最大应力随蒸汽腔内外压差增大而增大,两者呈正比例关系。
(5)在以上结论的基础上,归纳出了支撑柱直径、孔隙率、板厚和内外压差对最大应力共同作用的函数关系式,通过该关系式可以对不同结构参数蒸汽腔的最大应力进行合理预估,对大面积超薄蒸汽腔的设计具有一定参考价值。
由于蒸汽腔在不同应用场景下的复杂热源条件,本文未将温度梯度对腔体应力的影响纳入考虑,未来需要更加全面地进行热应力评估,即结合蒸汽腔内工质的相变换热,求解腔体的温度场,分析热应力对腔体力学性能的影响。

