采动岩层全空间“类双曲面”立体移动模型
左建平李颖李宏杰于美鲁吴作启刘家顺
1.中国矿业大学(北京)力学与建筑工程学院,北京 100083;2.煤炭资源与安全开采国家重点实验室,北京 100083;3.煤炭科学技术研究院有限公司安全分院,北京 100013;4.中煤科工生态环境科技有限公司,北京 100013;5.辽宁工程技术大学土木工程学院,辽宁阜新 123000
煤炭资源采掘或者地下工程开挖会造成上覆岩层整体性发生移动甚至破坏,出现顶板覆岩非连续破断及地表沉降现象,如地表裂缝、沉陷坑等。我国华东和西部矿区存在较厚松散层,以往的地表沉降预测大多基于经验法、概率积分法等。现场大量实测和理论表明,厚松散层条件下覆岩采动运移规律与薄松散层、无松散层条件下采动岩层移动规律存在差异[1-3]。
近年来,国内外学者在采动覆岩破断与开采地表沉陷方面进行了深入研究,并取得一定的成果。钱鸣高等[4-7]建立了采场上覆岩层移动的关键层控制理论,以关键层作为岩层移动的主要承载体,为岩层移动和地表沉陷的研究提供了一种统一的思想和方法;郭文兵等[8]认为覆岩破断、地表变形破坏与开采强度有关,揭示了高强度开采覆岩“两带”破坏模式的形成机制,总结了我国高强度开采覆岩与地表破坏的规律;许家林等[9-10]基于关键层理论研究了其对覆岩及地表移动的影响;于斌等[11-12]基于特厚煤层开采条件研究了远场覆岩结构失稳机理;黄庆享等[13-14]以陕北典型浅埋煤层群开采为工程背景,研究了煤层群开采覆岩裂缝的发育规律和形成机理。
左建平等[15]基于关键层理论将覆岩移动和地表沉陷建立联系,确定了岩层移动与地表沉陷的力学边界条件,建立了厚松散层覆岩移动的“类双曲线”模型,并发展了适用性更强的“类双曲线”识别模型[16-20];进而,以岩层移动边界“类双曲线”模型为基础,建立了岩层移动内外“类双曲线”整体模型[21]。这些理论模型大多数是基于二维平面的,而现场采矿工程是在三维空间里的采掘活动,故厚松散层覆岩的非连续破断以及岩层三维立体移动模型有待进一步研究。
随着绿色开采科学内涵不断丰富,基于数学力学分析模型来解释采动岩层空间移动规律与地表沉降之间的复杂关系更具科学意义[22-25]。本文基于关键层理论,以岩层移动内外“类双曲线”整体模型为基础[21],将基岩非连续破断与地表沉降建立联系并推广到三维空间,为认识三维空间厚松散层覆岩立体运移提供科学指导。
1 岩层“类双曲线”移动模型
1.1 采动岩层外“类双曲线”移动模型
大量工程实践与理论研究表明,岩层移动实质上是采场围岩开挖导致内部应力场发生变化引起的覆岩移动,而覆岩移动又进一步造成其内部应力场发生变化的过程[26-28]。文献[15-16]通过关键层理论将基岩移动、松散层以及表土层移动建立联系,提出了厚松散层覆岩移动外“类双曲线”模型(图1),且主关键层是岩层移动中损伤破坏最小的岩层。

图1 厚松散层覆岩“类双曲线”整体移动模型[15]Fig.1 Analogous hyperbola movement model of overlying rock strata with thick alluvium[15]
地下工程的采掘活动从极限跨距至充分采动期间,上覆基岩会发生初次破断和周期破断,且岩层破断规律具有周期性和非连续性。文献[15-16]通过对基岩初次断裂与周期断裂的应力状态进行力学分析,揭示基岩倒漏斗型破断机理;又从力学角度将厚松散层移动过程分为滑移—拉裂—剪断3个阶段。由于松散层的抗剪强度较低,与水平面夹角为45°+φ/2 时易发生剪切破坏;且随着松散层压实程度的减小,靠近表土层内摩擦角减小,从而揭示厚松散层漏斗型移动机理。
1.2 采动岩层内外“类双曲线”移动模型
文献[21]将厚松散层开采岩层移动与地表沉陷建立联系,提出了厚松散层岩层移动内外“类双曲线”模型,如图2所示。

图2 岩层移动与地表沉降共轭内外“类双曲线”整体移动模型[21]Fig.2 Conjugate analogous hyperbola model of strata movement and surface subsidence[21]
厚松散层地表沉陷曲线近似下凹型碗状拱形,采空区冒落带近似上凸型拱形,两者在几何形态上关于主关键层近似呈轴对称状。文献[21]对冒落拱与裂隙拱进行了临界力学分析,揭示了采空区上覆岩层的拱形冒落破坏实质为稳定裂隙区岩体间的极限剪切破坏;在工作面中部,可能形成拱状的砌体梁结构平衡关系,当砌体梁结构发生滑动极限失稳时,即为“梯形”倒漏斗拱状结构滑落[29],从力学角度解释了裂隙带大结构岩层的倒漏斗拱形特征。随工作面的推进,冒落拱与裂隙拱发生扩展和移动,为其余岩层的滑落与回转提供了空间,从而对地表沉陷的范围产生影响。
从数学角度来讲,内外“类双曲线”模型有一定的合理性。“类双曲线”的实轴和虚轴(图2中两条黄色虚线)可由罗尔中值定理得出:由于本文弯曲下沉带与冒落带曲线用外“类双曲线”描述,故两带曲线在变形区间内连续且可导,那么在变形区间内至少存在一个导数为零的中值点,即冒落带的最高点与地表沉降带的最低点。将外“类双曲线”上的中值点连接得到x轴,同样开采前后的内“类双曲线”也在变形区间内存在一个导数为零的中值点,连接即为z轴。
吴作启[30]以神东矿区典型厚松散层薄基岩采煤工作面为背景,通过相似模型试验及现场实测得到其覆岩变形特征。试验结果表明,厚松散层覆岩整体移动边界呈现内外“类双曲线”特征[21],如图3所示。

图3 相似模型试验采后状态[30]Fig.3 Post harvest state diagram of similar model test[30]
2 岩层移动“类双曲线”相似模型试验研究
2.1 相似模型试验设计
为进一步研究不同地质条件的岩层移动规律,以哈拉沟煤矿22208 工作面地质和开采条件为研究背景[30],运用相似模型试验台模拟其煤层开采过程,监测和记录相似材料模型在采中和采后采空区上覆基岩及松散层移动、变形和破坏特征。设计相似模型试验尺寸为:长×宽×高=2.2 m×0.3 m×1.2 m,将原地层按1 ∶100 缩小,模型为全地层模拟,顶部不施加外力。各岩层主要物理力学参数见表1。

表1 各岩层主要物理力学参数[30]Table 1 Main physical and mechanical parameters of rock strata[30]
2.2 试验结果与讨论
哈拉沟煤矿22208 工作面相似模型试验如图4所示。为消除边界影响,在试验台右侧预留50 cm,采前状态如图4(a)所示。当工作面开采至34.7 cm时,采空区顶板岩层达到承载极限后发生初次破断,此时,垮落高度约为2.5 cm,覆岩运移处于初期破断阶段,如图4(b)所示。当工作面推进至40 cm时,顶板岩层发生碎胀扩容,逐渐向采空区垮落并充实采空区,破断岩层呈现漏斗型上凸状,在向上发育过程中向内收敛,逐渐形成了“类单叶双曲面”模型腰线,两腰线位置分别对应初次断裂迹线和周期断裂迹线,垮落高度约为10 cm,覆岩运移处于中期内敛阶段,如图4(c)所示。当工作面开采至50 cm 时,上覆岩层运移相互联动,具体表现为大面积垮落、横向裂隙发育、纵向裂隙贯通、弯曲下沉形成离层。垮落区域由煤层顶板向上发育直至表土层,呈现出由两侧向内缓降的碗状下沉趋势,岩层移动边界整体初次显现为内外“类双曲线”。此时,覆岩运移处于末期沉降阶段,如图4(d)所示。随着工作面开采的进行,采动岩层的垮落与下沉表现出周期性破坏特征,覆岩运移处于周期显现阶段,覆岩形变状态至试验最终状态,如图4(e)(f)所示。
图4(f)中两条黄色虚线可分别由中值定理得出,在地表沉降曲线和冒落拱曲线中含有2个中值,中值处的导数为零,连接中值点得到竖直线;相同地,在水平方向看,最外层位移边界曲线也含有2个中值,连接中值点得到水平线。
3 岩层移动“类双曲面”立体移动模型
采矿工程实质是在立体空间内地下煤岩体的采掘活动。为了更直观地描述采动覆岩至地表移动特征,须将采动岩层移动表征为上覆岩层的空间运动行为。从解析几何的角度出发,结合实际工况,赋予代数方程明确的工程物理意义。图5是采动岩层三维空间立体移动模型,其中,走向剖面[图5(a)]和倾向剖面[图5(b)]都可以通过相似模型试验得到;平面图[图5(c)]中的地表裂缝规律可以通过现场裂缝分析获得。文献[31-34]表明,厚松散层薄基岩煤层地表裂缝发育的平面几何形态呈现椭圆O 型圈状。建立采动岩层移动与开采沉陷的二维模型[15-21],将采动岩层移动及地表沉陷有机联系并推广到三维空间,更精细地表征岩层移动和地表沉陷的空间运移规律。
本文以关键层理论为基础,进一步建立采动岩层移动与开采地表沉陷的空间立体“类双曲面”的数学力学模型,如图5(d)所示。需要说明,类双曲面模型是在厚松散层地质条件下推广的,但其对不同覆岩条件也有普适性。由于覆岩移动与岩层结构稳定性相关,而岩层结构稳定性又与主关键层下部基岩厚度及其上方松散层厚度紧密联系,则覆岩位移区和地表沉降范围会发生变化。具体表现为基岩的厚度和摩擦系数决定“类双曲面”模型的拐点,松散层的厚度和内摩擦角对“类双曲面”模型的开口大小起决定性作用,从而影响地表沉降的范围。不同的地质条件无非是松散层与基岩厚薄的情况,模型的形状会稍有改变,但覆岩移动区整体符合类双曲面趋势,均是类双曲面模型的拓扑演化。
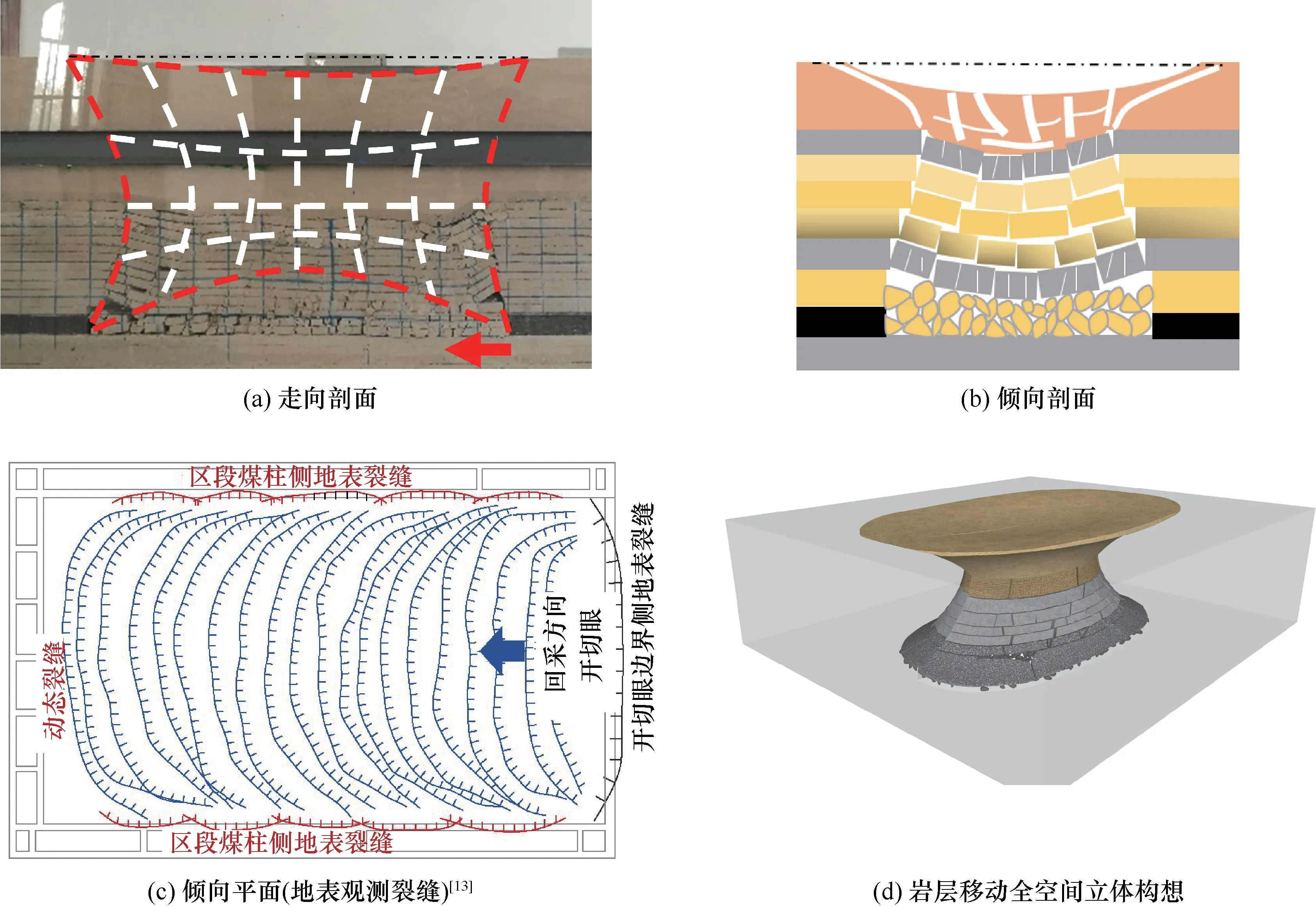
图5 采动岩层三维空间立体移动模型Fig.5 Three-dimensional moving model of mining rock strata
3.1 采动岩层空间“类单叶双曲面”模型
3.1.1“类单叶双曲面”模型建立
在空间上采动岩层移动边界为一近似的单叶双曲面形状,但不同于严格数学意义上的单叶双曲面,不同的地质及开采条件也会形成不同的双曲面,不过在实际采矿工程中均与该曲面有一定的相似性,所以本文用“类单叶双曲面”来近似描述该模型,采用数学表达式及双曲面图形来表征,如图6所示。
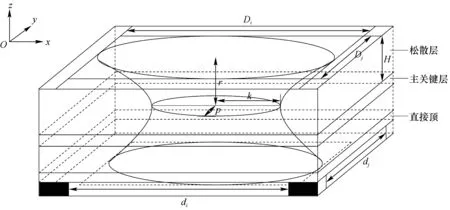
图6 采动岩层空间“类单叶双曲面”模型Fig.6 Analogous single leaf hyperboloid model of mining strata space
根据图6,用单叶双曲面的标准方程来近似表示空间采动岩层的整体位移边界:
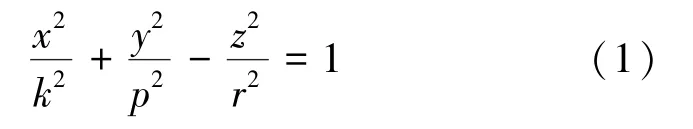
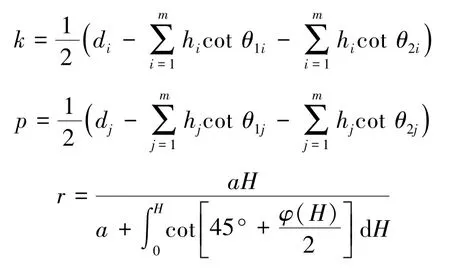
式中,a为任意剖面方向顶点到坐标原点的距离;di为工作面推进距离;dj为工作面布置长度;H为松散层厚度;m为基岩中的岩层数;hi=hj为基岩中岩层的厚度;θ1i,θ2i分别为x方向基岩中不同岩层的初次垮落角和周期垮落角;θ1j,θ2j分别为y方向基岩中不同岩层的初次垮落角和周期垮落角;φ(H)为随松散层深度H变化的厚松散层内摩擦角。
3.1.2“类单叶双曲面”模型分析
为了进一步认识这个模型,借助平行截割法[35],利用一族平行平面来截割模型,进而研究截口曲线(曲面与平面的交线)的变化状态,把复杂的岩层整体水平移动空间曲面归结为容易认识的平面曲线(表2)。
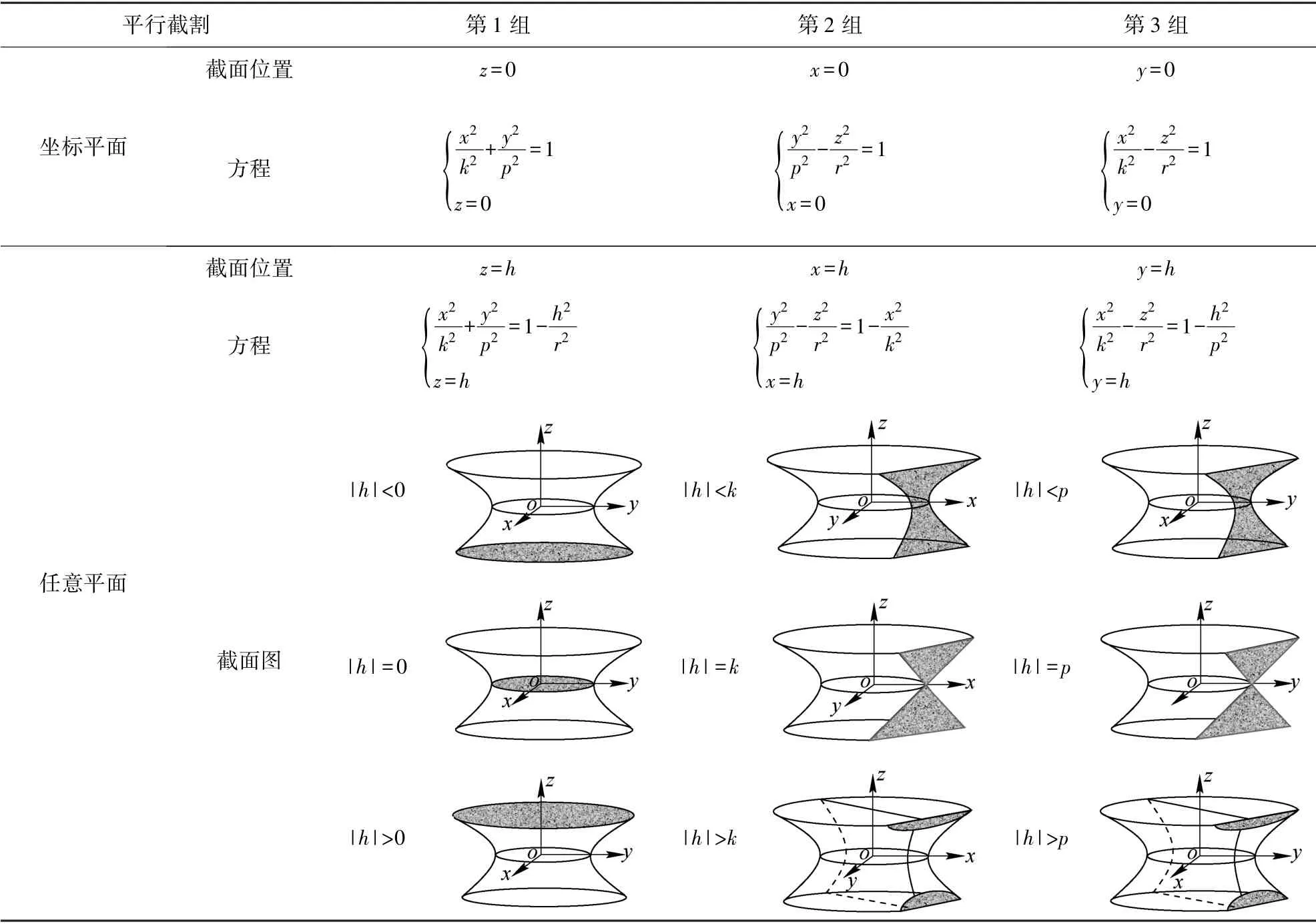
表2 平行截割“类单叶双曲面”模型Table 2 Parallel cutting of analogous single leaf hyperboloid model
3.2 岩层移动与地表沉降空间“类双叶双曲面”模型
3.2.1“类双叶双曲面”模型建立
若不考虑岩性变化、断层构造、陷落柱以及开采方式等因素,在厚松散层水平煤层开采条件下(同3.1),以主关键层为基础建立笛卡尔坐标系。针对地表开采沉陷曲面、冒落拱与裂隙拱曲面,建立空间立体“类双叶双曲面”模型,如图7所示。该模型能近似描述开采地表沉陷与岩层垂向移动的空间立体关系。
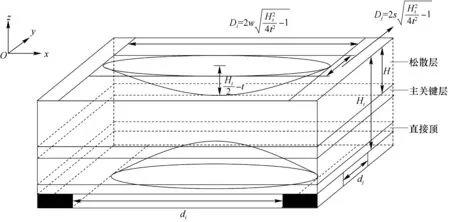
图7 采动岩层空间“类双叶双曲面”模型Fig.7 Analogous double leaf hyperboloid model of mining strata space
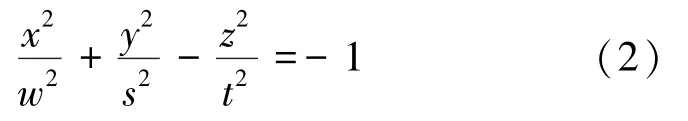
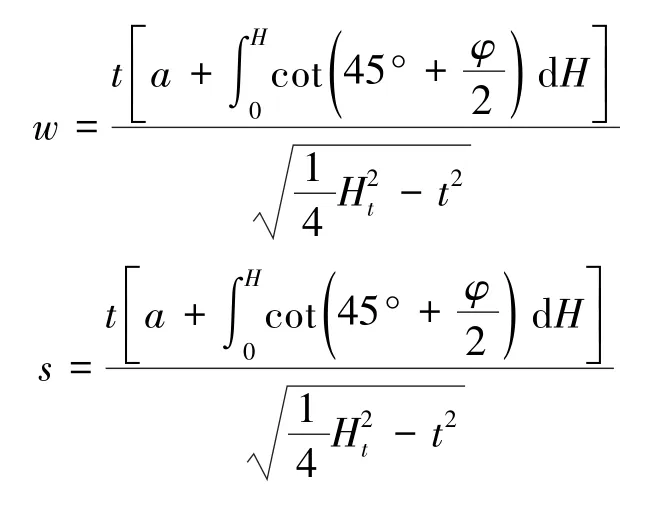
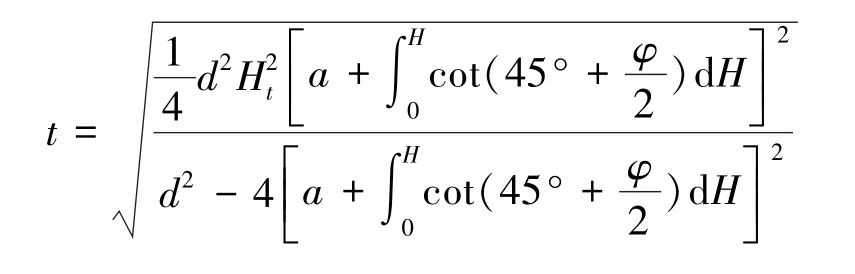
式中,t为地表沉陷最低点到主关键层的垂直距离;Ht为煤层埋深。
3.2.2“类双叶双曲面”模型分析
“类双叶双曲面”模型分析列于表3。

表3 平行截割“类双叶双曲面”模型Table 3 Parallel cutting of analogous double leaf hyperboloid model
3.3 “类双曲面”模型拓扑演化
为进一步研究工作面不同开采布置方式下“类单叶双曲面”模型的响应变化,以工作面走向长度和倾向长度为主要因素,以类双曲面俯视剖面(图8)为评价指标,进行不同工作面布置下的敏感性分析,揭示不同工作面布置条件下岩层移动类双曲面模型的演化形态(表4)。结果表明:固定工作面倾向长度、工作面走向长度逐渐增大时,模型俯视剖面主要沿走向扩展;固定工作面走向长度、工作面倾向长度逐渐增大时,模型俯视剖面主要沿倾向扩展。
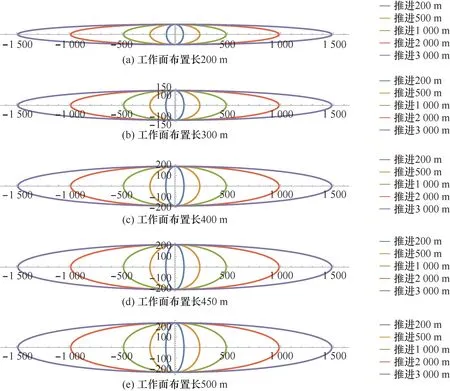
图8 不同工作面布置下俯视剖面变化Fig.8 Variation of top view section under different working face arrangements

表4 不同开采条件下“类单叶双曲面”模型的拓扑演化规律Table 4 Topological evolution law of analogous single leaf yperboloid model under different mining conditions
3.4 “类双曲面”模型有共同渐近锥面条件
以岩层移动内外“类双曲线”整体模型为基础,将物理参数k、p、r和w、t、s联系,建立空间立体“类双曲面”模型,参数受工作面推进距离、工作面布置长度、煤层埋深、覆岩和厚松散层高度等的影响。若采动岩层全空间“类双曲面”立体移动模型中的物理参数满足k≈t、r≈w、p≈-s时,即这组模型与坐标平面相切的曲线均有近似共同渐近线,“类双曲面”模型关于坐标轴近似对称,类双曲面的截口椭圆与渐近锥面的截口椭圆任意接近,近似重合,则“类单叶双曲面”与“类双叶双曲面”在式(3)和式(4)对应的曲线处近似相切,且有共同的渐近锥面,其函数表达式见式(5),称为共渐进锥面“类双曲面”模型。此时,“类双曲面”模型退化对应的“类双曲线”模型为近似共轭双曲线。
操作盘被毁,大家以为这下连船带人都要粉身碎骨了。忽然,船身停止了晃动。准确地说,是飞船完全静止在原处。奇巧生告诉大家操作盘被毁,触发了飞船的紧急自降功能,飞船会安全着陆。
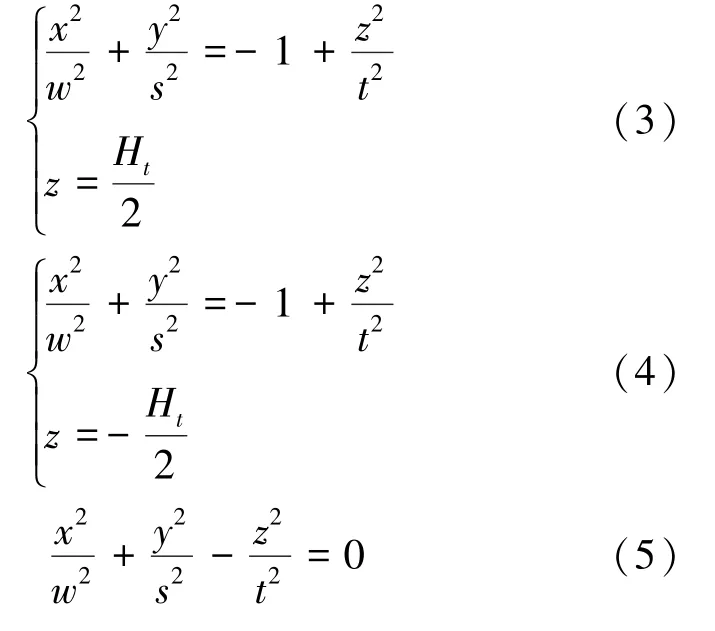
需要注意,在实际工程中受复杂地质条件的影响,“类双曲面”模型相切为一个特例。若采动岩层全空间“类双曲面”立体移动模型有近似相切关系时,则松散层沉降角有如下近似关系:

3.5 “类双曲面”和“类双曲线”的退化分析
由于在建模过程中引入了多种假设条件,为验证模型的适用性、合理性及有效性,借助退化验证(复杂的函数在某种条件下变成一个简单的函数,维数次序的降低),即仅考虑工作面布置方向或推进方向,对上述“类双曲面”模型进行检验。
3.5.1“类单叶双曲面”模型退化验证
当y=0 时,类单叶双曲面退化为二维类双曲线:
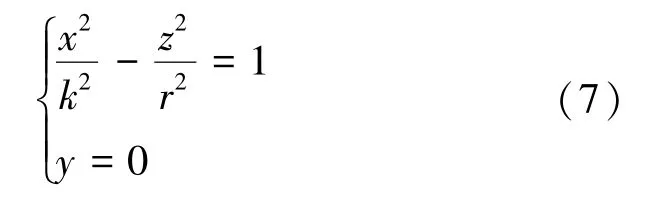
式(7)符合文献提出的厚松散层岩层移动边界外“类双曲线”模型[15],其中k等价于a,r等价于b。
同理,在x=0 时,类单叶双曲面退化为二维类双曲线:

3.5.2“类双叶双曲面”模型退化验证
当y=0 时,类双叶双曲面退化为二维类双曲线:
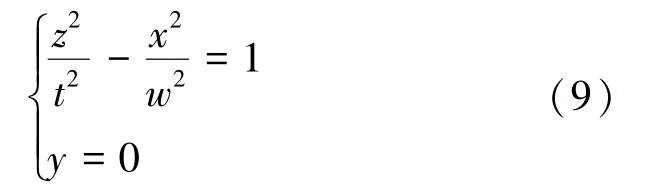
式(9)符合文献[15]提出的岩层移动与地表沉降内“类双曲线”模型,其中t等价于m,w等价于n。
同理,在x=0 时,类双叶双曲面退化为二维类双曲线:

式中,y=0,为退化工作面布置方向;x=0,为退化工作面推进方向。
岩层移动“类双曲面”立体模型描述了岩层在三维空间的移动规律,它可退化为二维的岩层移动“类双曲线”平面模型,也就是说内外“类双曲线”模型是立体模型在二维条件下的描述。
4 厚松散层超长工作面覆岩移动的3DEC模拟
三维离散元程序(3DEC)适合模拟非连续介质(节理岩石)在结构面切割块体的非连续力学行为,运用该软件可模拟采动岩层在煤层开采过程中的破断规律。
4.1 模型建立
以哈拉沟煤矿22208 工作面工程地质条件为背景,运用3DEC 建立相应的数值计算模型,模拟超长工作面开采时“类双曲面”形成的第一个周期。模型(图9)长×宽×高=600 m×500 m×124 m,模拟1 号煤层22208 工作面倾向长245 m,走向长400 m,其中岩层根据1 号煤层工作面顶板自下而上划分了9 组,煤层厚度5 m,直接顶为砂岩,基本顶为泥岩,主关键层为序号5 对应的中砂岩,各岩层中生成随机裂缝[18,36]。数值模型四周和底部边界通过位移固定,数值模拟中岩块采用莫尔-库仑模型,节理面采用库伦-滑移模型。煤岩体主要物理力学参数见表1。

图9 哈拉沟煤矿3DEC 数值模型Fig.9 3DEC numerical model of Halagou coal mine
4.2 计算结果与讨论
通过3DEC 模拟了工作面不同推进距离(40 m,80 m,120 m,160 m,200 m)时采动岩层整体运移过程和地表沉陷规律。为了更直观地展示模拟云图,均采用3个法方向切片平铺的方式,立体效果如图10所示。当工作面推进40 m时,采空区中部顶板位移明显大于两端头处并呈现向上阶梯发育趋势,处于初期破断阶段,如图10(a)所示;当工作面推进80 m 时,基本顶破断形成铰接结构,关键层位置处发生破断,上覆岩层整体呈倒漏斗型上凸状,如图10(b)所示;当工作面推进至120 m 位置处,采空区顶板垮落形成冒落拱,关键层位置处岩层弯曲下沉产生离层,地表采动损伤影响范围较小,地表沉降处于中期内敛阶段,如图10(c)所示;当工作面回采至160 m 时,冒落拱内破碎的煤岩体被逐渐压实,覆岩裂隙相互贯通并向上发育至主关键层,进而形成裂隙拱,顶板岩层的弯曲下沉与地表沉降的范围成正相关关系,此时厚松散层地表下沉表现为两侧向内缓慢的碗状下沉趋势,岩层移动边界整体初次显现为内外“类双曲线”,进入末期沉降阶段,如图10(d)所示;当工作面推进200 m 时,地表下沉体积已趋于稳定,采动岩层整体移动边界均相应扩展,在水平面均呈现“类双曲线”特征,在垂直方向呈现类似椭圆O 型圈状,进入周期显现阶段,如图10(e)所示。
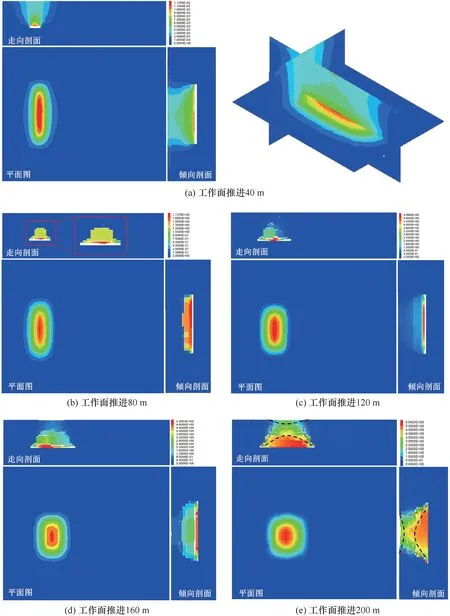
图10 岩层移动与地表沉降“类双曲面”形成位移云图Fig.10 The “hyperboloid” of rock strata movement and surface subsidence forms the displacement cloud map
5 结 论
基于岩层移动内外“类双曲线”二维模型及相似模型试验,本文进一步提出采动岩层全空间“类双曲面”立体移动模型,结合数值模拟分析得到结论如下:
(1) 通过哈拉沟22208 工作面相似模型试验,获得了厚松散层条件下覆岩移动和地表沉陷整体移动特征,验证了岩层移动内外“类双曲线”模型的有效性。
(2) 基于岩层移动内外“类双曲线”平面模型及相似模型试验,在三维空间上分析了空间厚松散层覆岩移动与开采沉陷整体运移机理,由此建立了采动岩层全空间“类双曲面”立体移动模型。该模型包括“类单叶双曲面”模型和“类双叶双曲面”模型,分别在水平面和垂直方向描述了采动裂隙的演化规律。
(3) 分析了采动岩层全空间“类双曲面”立体移动模型有共同渐近锥面的构成条件、影响因素及运移规律。空间采动岩层移动与地表沉陷“类双曲面”立体移动模型的形成受煤层赋存条件影响,其中松散层厚度、主关键层下部直接顶厚度和推进距离对模型有直接影响。
(4) 运用3DEC 模拟了典型厚松散层近水平煤层工作面开采,获得了空间采动覆岩移动和地表沉陷的发育规律:充分采动后覆岩整体呈“类双曲面”移动特征,一定程度上验证了“类双曲面”立体模型的合理性。

