挡墙绕顶转动墙后被动土压力研究

张 航，齐永正

(1.南京江宁交通建设集团有限公司, 江苏 南京 211100；2.江苏科技大学 土木工程与建筑学院，江苏镇江 212100；3.江苏省地质环境灾害防治及修复工程研究中心, 江苏 镇江 212100)

0 引言

土压力广泛地应用在各类工程中，挡土墙的设计往往需要考虑墙后土压力的分布形式。在实际应用中，当墙后土层成层分布时，土压力在土层分界处常常采用台阶式突变的分布模式计算墙后土压力。实际土压力分布规律如何，这种计算理论是否合理，对于工程设计与应用，关系到工程的结构安全，需引起高度重视。

顾帮全[1]重点分析了挡土墙墙后填土经有效处理后，墙后土所能产生的侧向土压力与墙后土的有效宽度之间的关系，引入了临界宽度Lp。研究发现，当L≤Lp时，墙后侧向土压力在后前土体有效宽度足够小的情况下，墙后土体破坏时所产生的侧向土压力随着墙后土体有效宽度L的增大而增大；当L>Lp时，墙后侧向土压力服从朗肯侧向土压力公式。

曹雄[2]通过将土压力理论与稳定计算联系在一起，推导出了复杂条件下的主侧向土压力计算式。并且给出了临界破裂角的显式解答，避免了通过试算确定主动土压力。

王杰[3]以平移模式下的刚性挡土墙为研究对象，对主动土压力和侧向土压力进行了研究。应用土拱效应原理分析墙后土体的应力状态和主应力偏转的情况，比较分析不同土拱形状的差异。定量分析了墙土接触面摩擦力对墙后填土应力状态的影响，解释了墙土接触面摩擦引起的主应力发生旋转。

马崇武[4]基于极限平衡理论，视墙后填土为服从Mohr-Coulomb屈服准则的理想弹塑性材料。考虑滑裂面上填土的黏聚力及填土与墙背接触面上的黏着力等因素，从滑楔体极限平衡状态时的静力平衡条件出发，应用静力平衡条件得到计算有荷载作用时黏性土和无黏性土侧向土压力的公式。基于侧向土压力的基本原理，假定挡土墙任意深度对应的滑移楔同时达到极限平衡条件，提出了求解土压力分布的数值方法。

刘涛[5]基于土体应力状态，推导了黏性土侧向土压力系数及被动层间摩擦系数的求解公式，给出了侧向土压力系数及被动层间摩擦系数变换方法。在绕顶转动模式下，由于土拱效应的影响，侧向土压力呈凹形非线性分布，并且随着墙土摩擦角与土内摩擦角的增大，绕墙顶转动时侧向土压力的非线性分布也会增强。

王国良[6]对考虑土拱效应的黏性土挡土墙侧向土压力进行了研究，给出了黏性土侧向土压力系数；用应力状态法求解出了绕墙顶转动下的挡土墙侧向土压力竖向平均应力及土压力合力及作用点。研究表明:由于土拱效应的影响，挡土墙侧向土压力呈上大下小非线性分布。

张智雄[7]从理论和数值计算上证明了挡土墙向土体方向发生一定水平位移，土体处于非极限状态时，墙后回填土体出现相对位移区，该区形状为倒梯形。墙体位移增大，土拱曲线曲率增大，曲线越弯曲；填土内摩擦角增大，土拱曲线曲率减小，曲线越平缓。

周亦涛[8]假定墙后无黏性滑裂土体的大主应力土拱迹线为圆弧线，考虑墙土摩擦角对墙后土体被动滑裂面倾角的影响，对水平微分单元层进行土拱效应分析发现：被动土压力随填土内摩擦角的增加而增加，且越远离墙顶增幅越大；被动土压力在墙顶附近随墙土摩擦角的增加而减小，在墙中下部却随墙土摩擦角的增加而增加，且越靠近墙底增幅越大；侧向被动土应力及侧向土压力随填土表面荷载、填土容重的增加而增加。

梁浩然[9]通过定性分析和定量计算，指出两种计算方法在破裂角的计算中均能给出一致的结果，但是由于两种方法推导中选取的计算微单元不同，侧向土压力的大小存在较大的差别，这种差别随着土体黏聚力的增加逐步加大。

程康[10]以墙后填土为非饱和土的刚性挡墙为研究对象，考虑土拱效应和水平微单元体层间剪切作用的影响，假定墙后土拱形状为抛物线形拱，结合水平单元分析法、朗肯滑裂面等，分别建立了平动模式下水平微单元体平均竖向应力、层间剪切力与侧向土压力的定量关系，推导了平移模式挡墙侧向土压力系数及侧向土压力解析解。

本文拟通过挡墙绕顶转动工况下4组不同土层模型试验，研究墙后水平侧向土压力分布规律，为工程设计与施工提供理论支撑。

1 材料和方法

1.1 试验材料

试验土样为宁镇地区下蜀土，土的物理性质指标如表1所示。

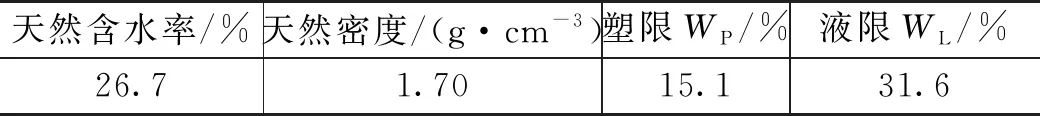
表1 天然土的物理性质指标

实验采用重塑土制备试验模型，通过控制含水率区分“硬土”和“软土”，设定含水率为15%的土样为硬土，含水率为30%的土样为软土。取回的土样经烘干后粉碎过10 cm筛。按照设定含水率，往干土中加水调配成相对的硬土和软土。对应物理力学指标如表2所示。

表2 硬土和软土抗剪强度性质指标

1.2 试验模型制作

模型箱由透明亚克力板制作，便于观察。模型箱内部尺寸为118 cm(长)×23 cm(宽)×72 cm(高)。模型箱正面标注土层分界线及5 cm×5 cm的网格线。挡墙由透明亚克力板和角钢固定贴合组成。加载端由钢架制成，用以施加水平荷载及监测挡墙位移。挡板一侧为土体，另一侧为加载和位移测量装置。加载装置为上下两台千斤顶，型号为FCY-20100；挡墙位移由4只百分表测量，量程100 mm，精度为0.1 mm，百分表位置如图1所示；土压力采用电阻应变式土压力计，量程1.0 MPa，土压力计设计位置如图2所示。

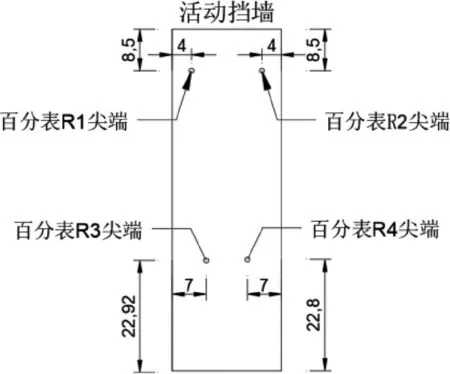
图1 百分表位置示意图(单位:mm)

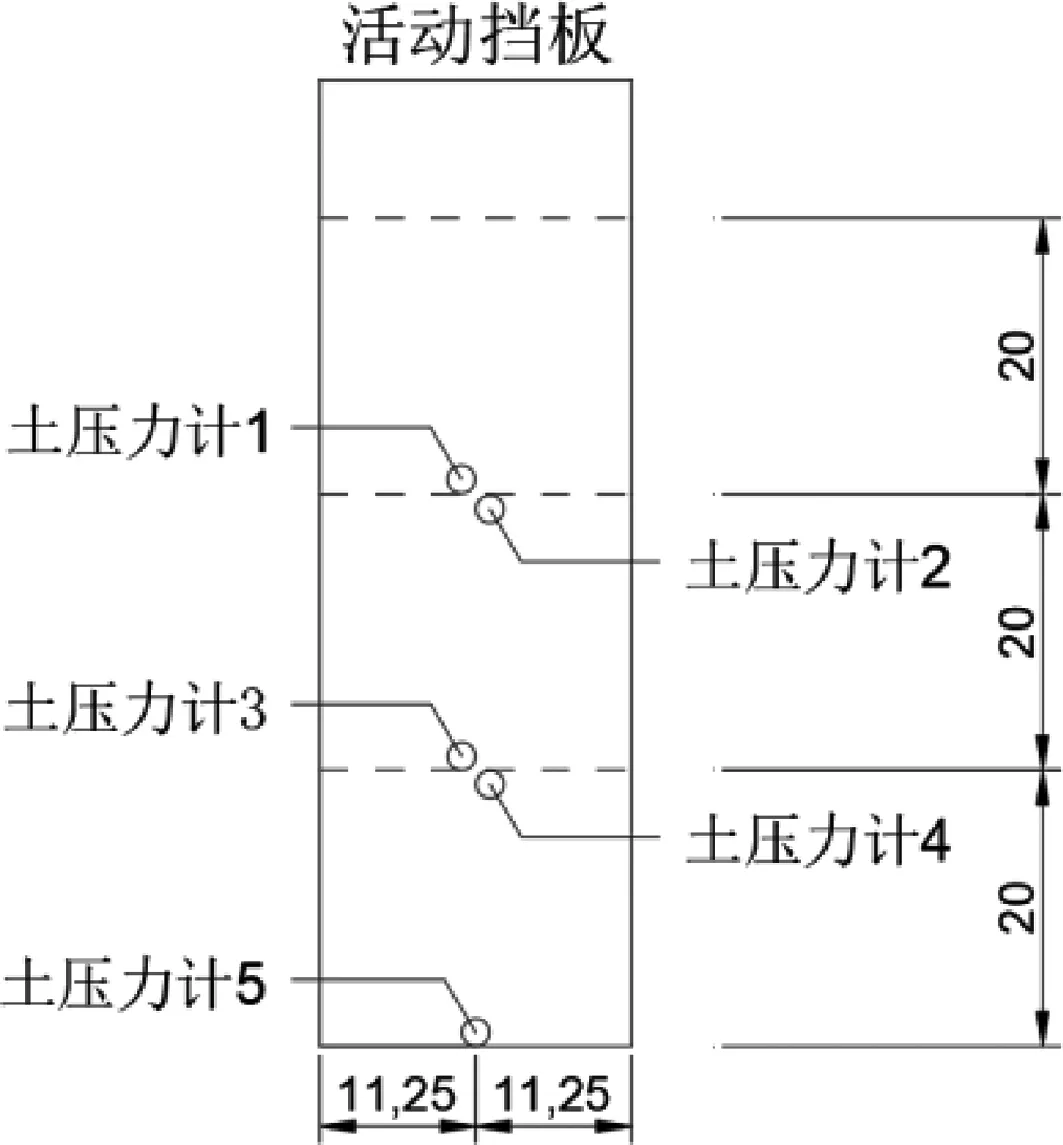
图2 土压力计位置图(单位:cm)

将土压力计分别固定在距离挡墙底部0 cm，19 cm，21 cm，39 cm和41 cm位置处，用导线引出，与数据采集仪相连。将活动挡墙推至与承载架紧密贴合，填充夯实土样，每层厚度20 cm，土体与箱体接触面之间放入干面条形成可视网格，以便观察到土体受载变形情况。试验模型如图3所示。

图3 试验模型俯视图

1.3 试验设计

试验分4组模型展开，分别为(1)单一硬土；(2)硬土-软土-硬土；(3)软土-硬土-软土；(4)单一软土，分析墙后水平侧向土压力分布规律。每组模型制作完成后，下部千斤顶加载，上部千斤顶保持不动，控制挡墙绕底转动，记录每次加载后的荷载值和挡墙位移值。总荷载70 kPa，分6级加载。

2 试验结果与分析

2.1 单一硬土模型试验结果

单一硬土试验模型加载前和加载结束土层变化如图4a、4b所示。第2级加载后挡板明显绕顶向土样侧倾斜，挡墙端土体表面开始隆起，随着后续加载，土体向上拱起，远离挡墙端隆起较多并逐渐向挡墙端下降。

图4 单一硬土模型加载前后土体变形

挡墙位移实测值如表3所示。

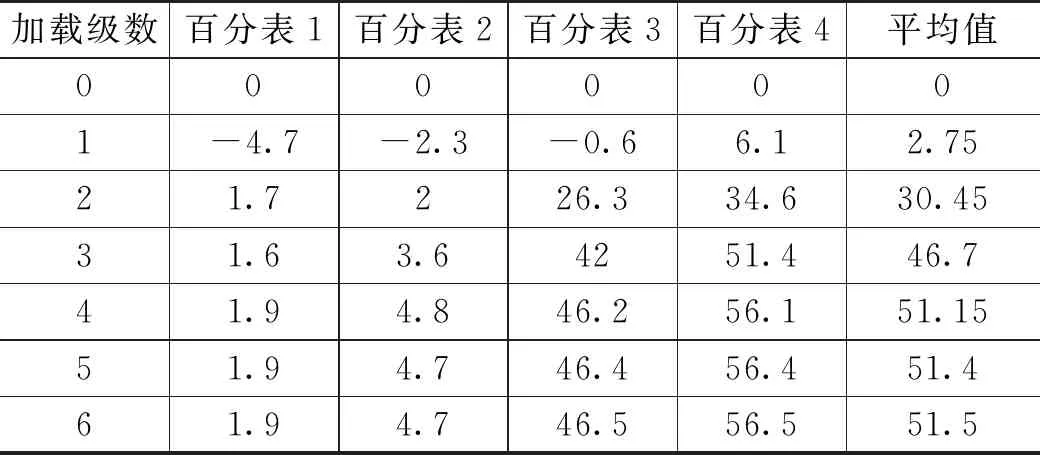
表3 单一硬土模型挡墙位移值 单位：mm

墙后侧向水平土压力监测数据如表4所示，墙后实测侧向水平土压力分布如图5所示。

由表4的数据和图5可知，对于单一硬土模型，土层交界处所测土压力基本相同，无应力突变，故仅选取土压力计1、3、5值进行分析。图6为单一硬土模型墙后侧向水平土压力随墙底位移变化曲线，由图6中的曲线可知，加载至第4级荷载后，继续加载，侧向水平土压力值不再增加，表明土体在第4级加载后已达到极限抗剪强度，土体剪切破坏，底部土压力增长远快于挡墙中上部，底部土层承担较大的外加荷载。

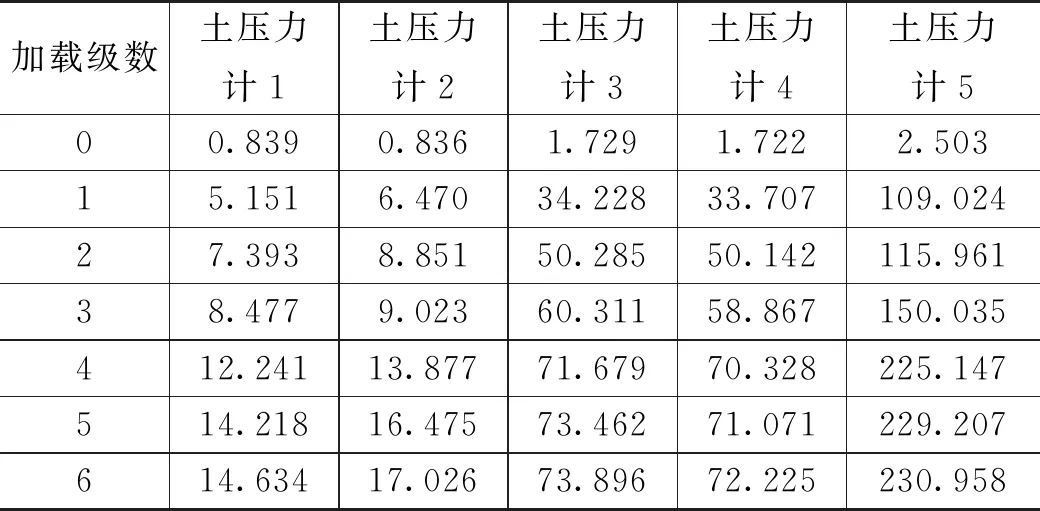
表4 单一硬土模型土压力监测数据 单位：kPa

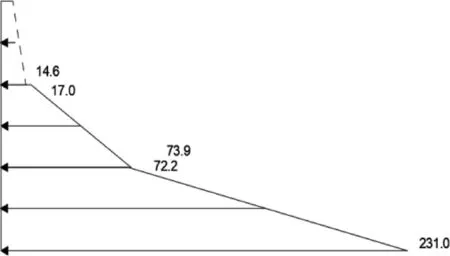
图5 单一硬土模型实测墙后土压力分布

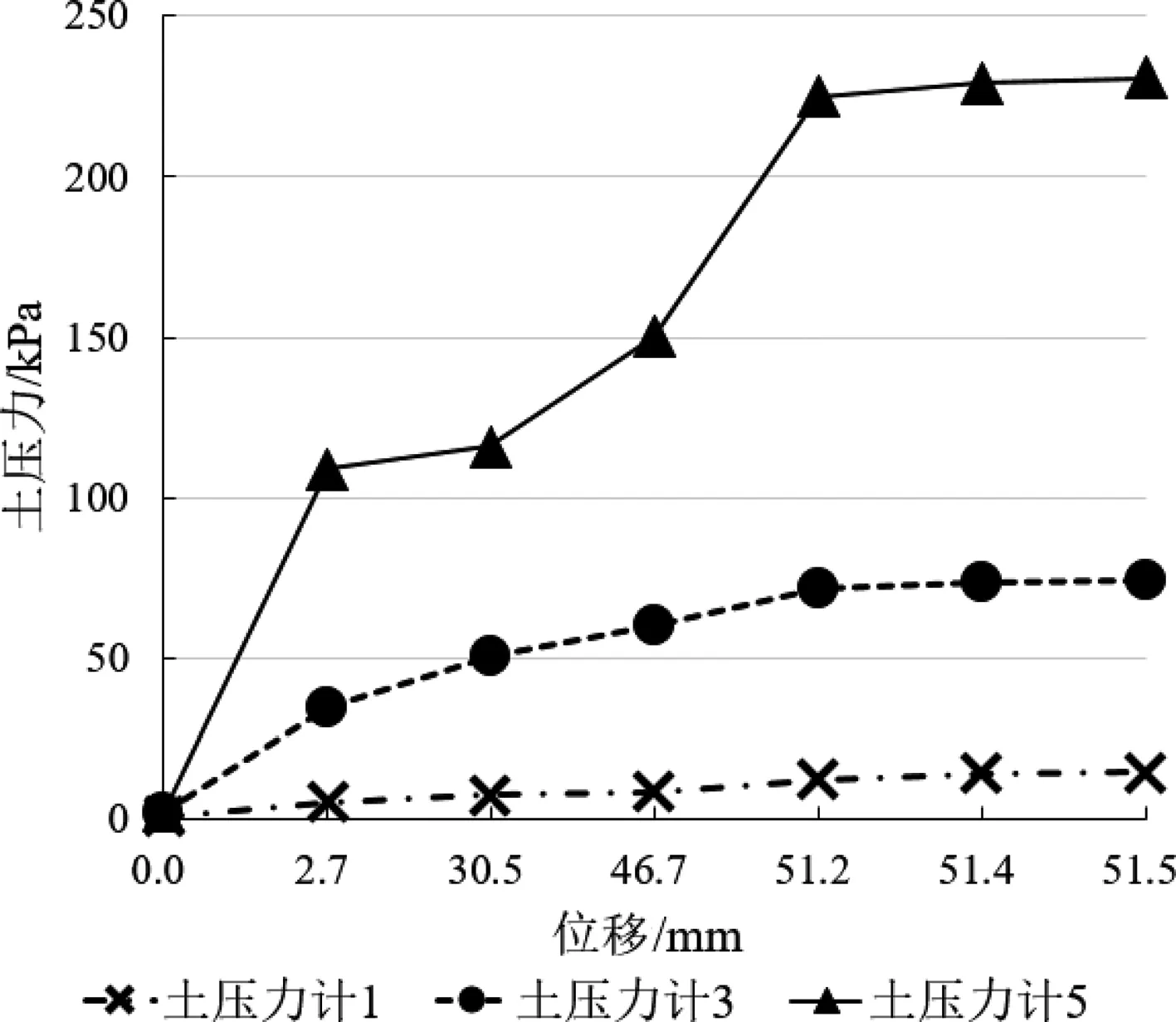
图6 单一硬土模型土压力随墙底位移变化曲线

2.2 硬土-软土-硬土模型试验结果

硬土-软土-硬土试验模型加载前和加载结束土体变形如图7a-7b所示。第2级加载后土体开始出现向上凸起的土拱，土体表面出现两道明显的环形褶皱，中间隆起较两边显著，如图7c所示。

图7 硬土-软土-硬土模型加载前后土体变形

挡墙位移实测值如表5所示。

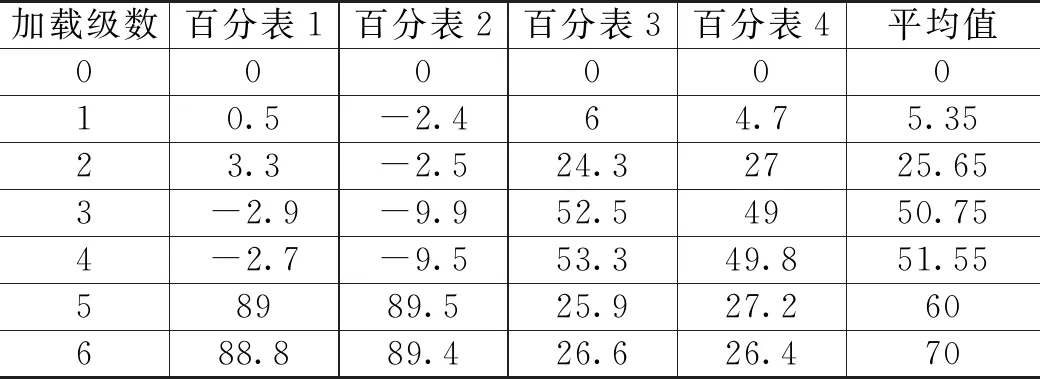
表5 硬土-软土-硬土模型挡墙位移值 单位：mm

墙后侧向水平土压力监测数据如表6所示，墙后实测侧向水平土压力分布如图8所示。

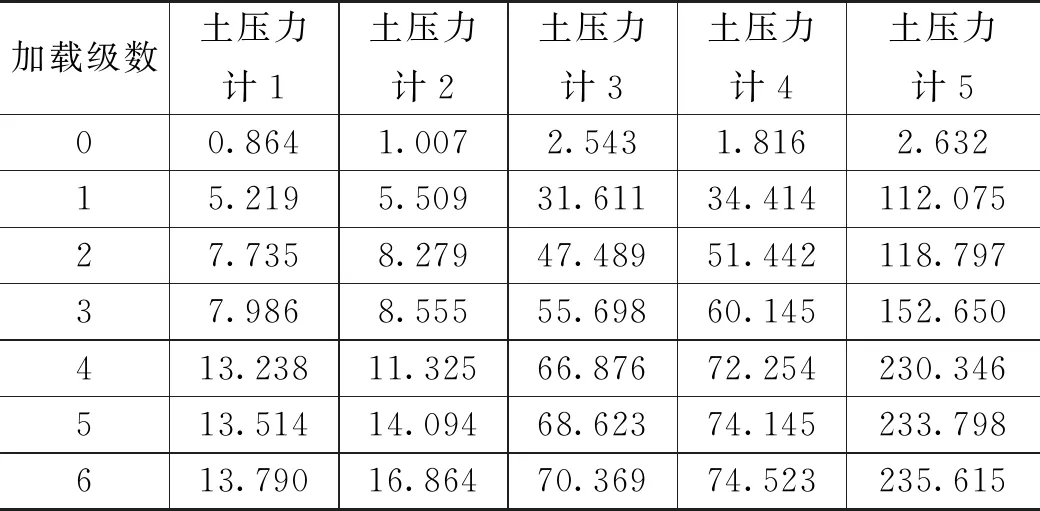
表6 硬土-软土-硬土模型土压力监测数据 单位：kPa

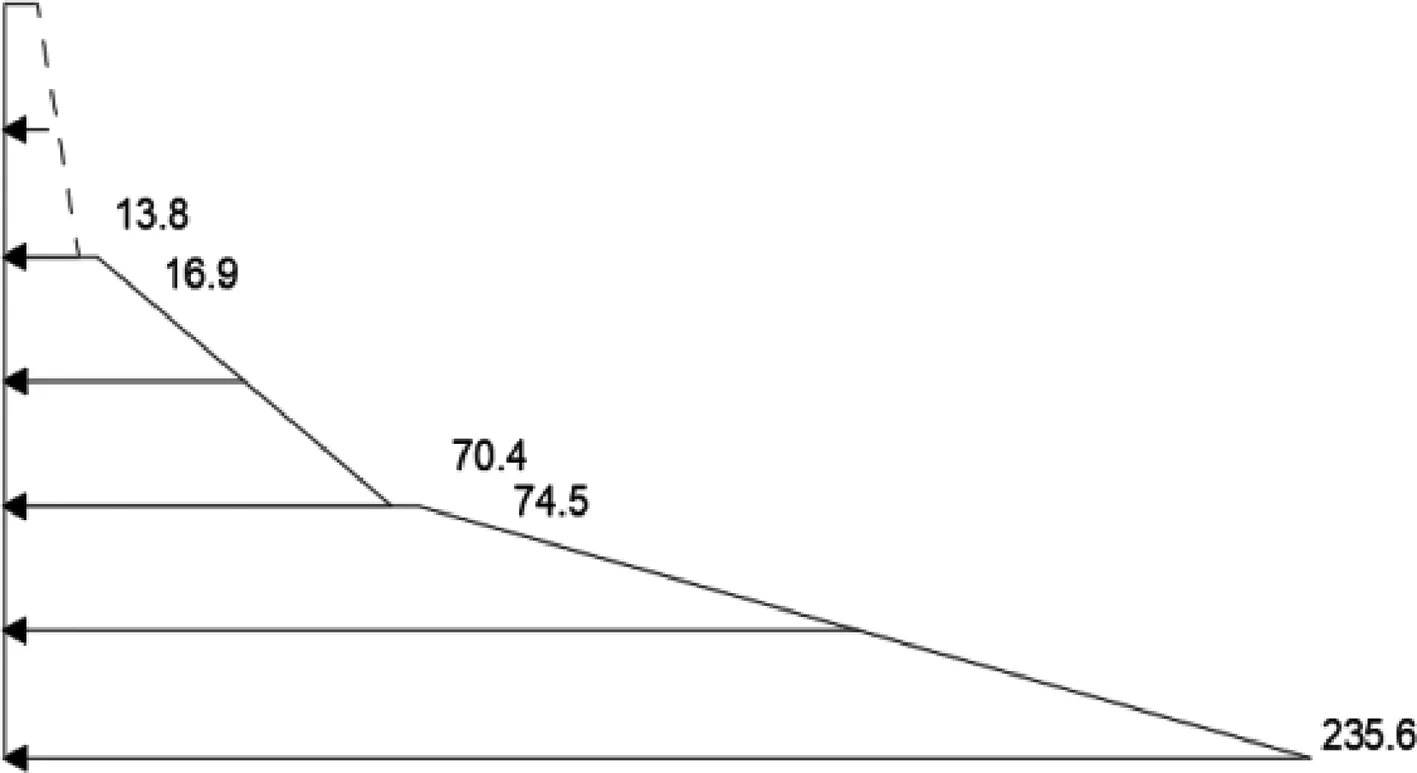
图8 硬土-软土-硬土模型实测土压力分布

由表5的数据和图8可知，对于硬土-软土-硬土模型，土层交界处实测土压力值出现明显差异，土层交界处存在应力突变现象。图9为硬土-软土-硬土模型土中侧向水平土压力随墙底位移变化曲线，由图9中的曲线可知，加载至第4级荷载后，继续加载，侧向水平土压力值不再增加，表明土体在第4级加载后已达到极限抗剪强度，土体剪切破坏，底部土压力增长远快于挡墙中上部，底部土层承担较大的外加荷载。

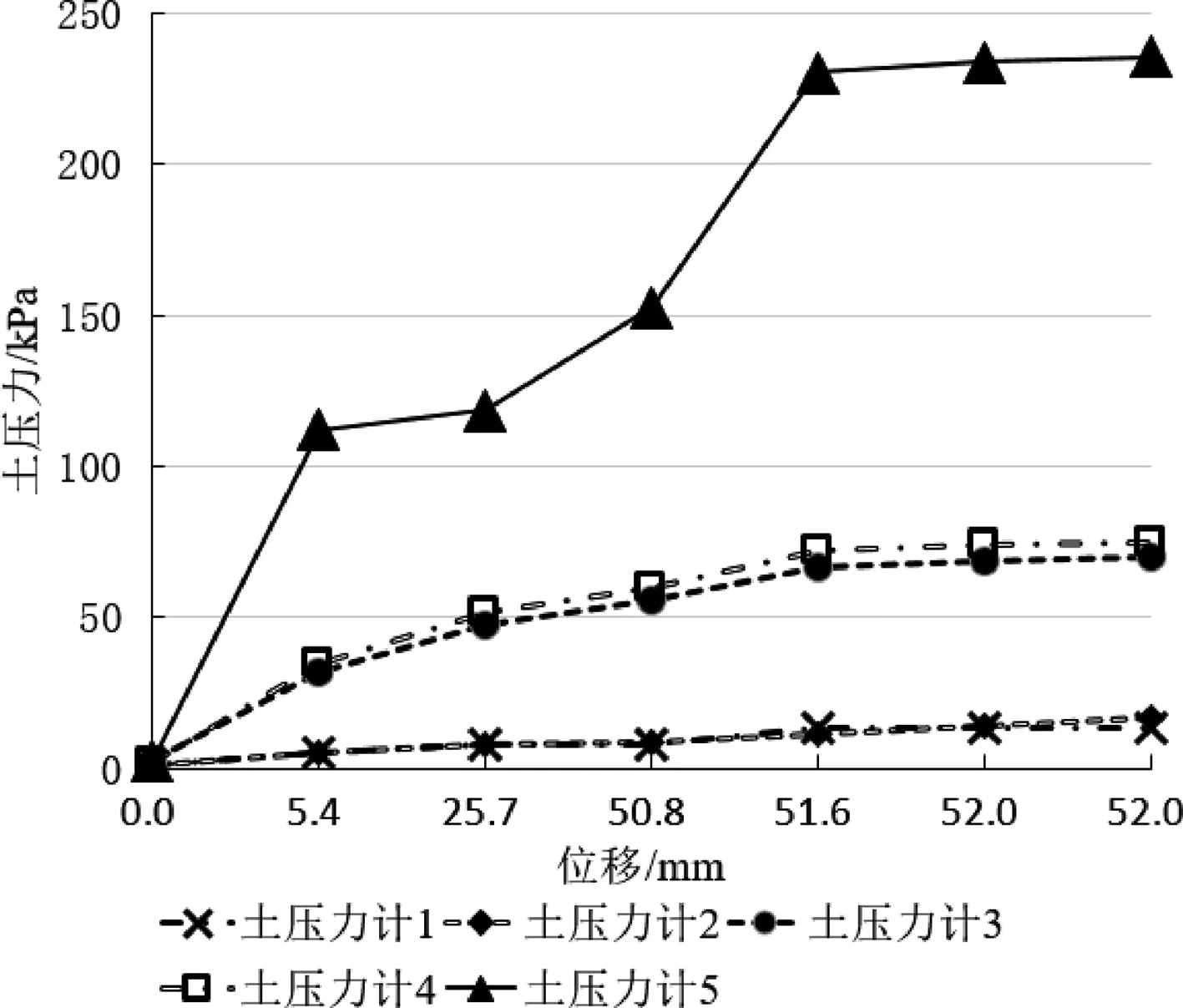
图9 硬土-软土-硬土模型土压力随墙底位移变化曲线

2.3 软土-硬土-软土模型试验结果

软土-硬土-软土试验模型加载前和加载结束土体变化如图10a、10b所示。第3级加载后，土体开始竖向隆起；加载结束，远离挡墙土体上部中间部分隆起较明显。

图10 软土-硬土-软土模型加载前后土体变形

挡墙位移实测值如表7所示。

表7 软土-硬土-软土模型挡墙位移值 单位：mm

墙后侧向水平土压力监测数据如表8所示，墙后实测侧向水平土压力分布如图11所示。

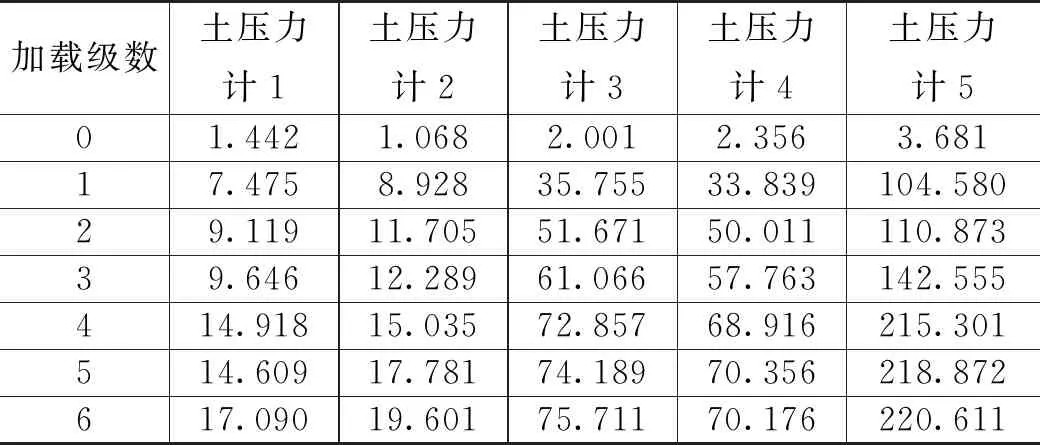
表8 软土-硬土-软土模型土压力监测数据 单位：kPa

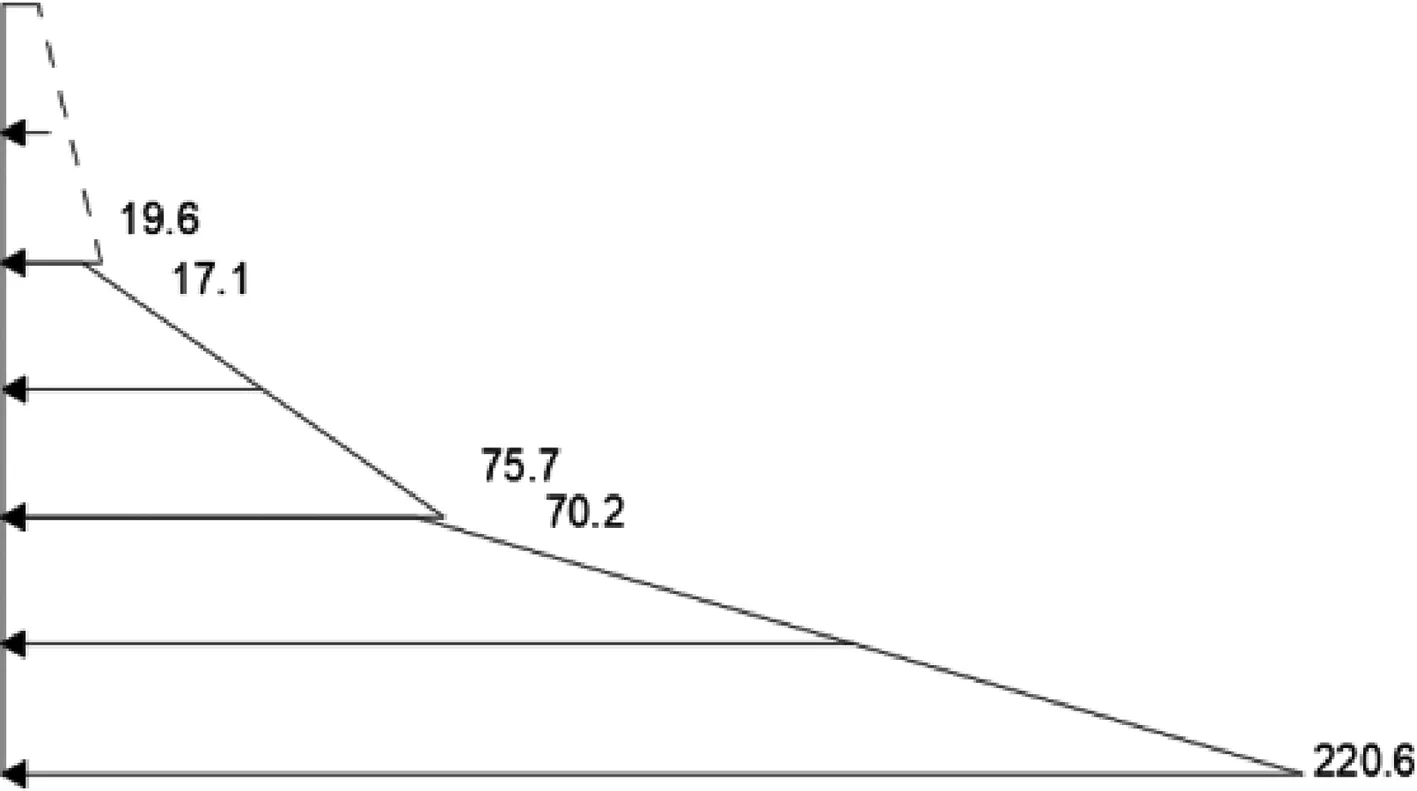
图11 软土-硬土-软土模型实测土压力分布

由表7的数据和图11可知，对于软土-硬土-软土模型，土层交界处实测土压力值出现差异，存在应力突变现象，但不明显。图12为软土-硬土-软土模型墙背侧向水平土压力随墙底位移变化曲线。由图12中的曲线可知，加载至第4级荷载后，继续加载，侧向水平土压力值不再增加，表明土体在第4级加载后已达到极限抗剪强度，土体剪切破坏，底部土压力增长远快于挡墙中上部，底部土层承担较大的外加荷载。

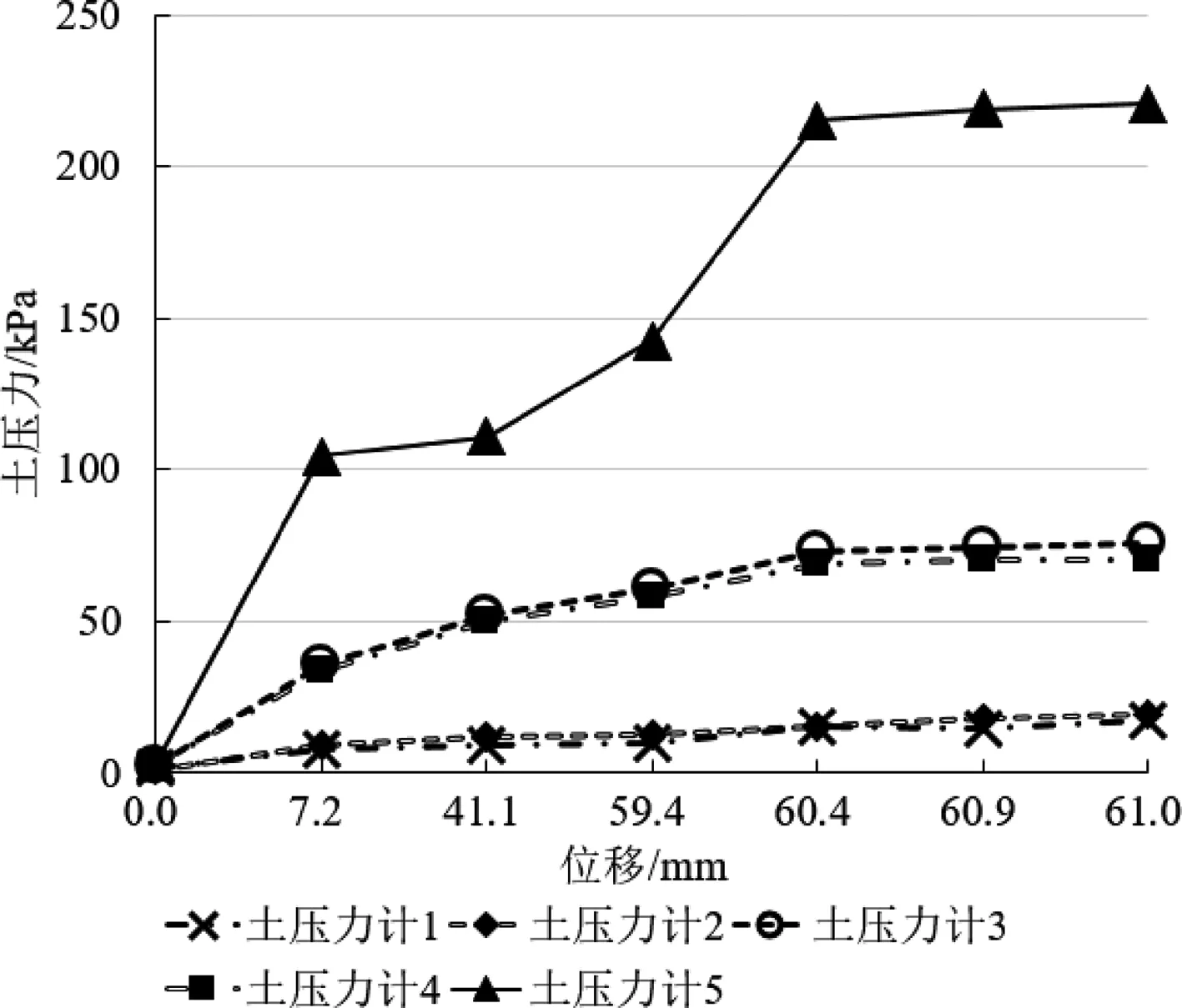
图12 软土-硬土-软土模型土压力随墙底位移变化曲线

2.4 单一软土模型试验结果

单一软土试验模型加载前和加载结束土体变化如图13a-13b所示。加载后，土体水平向压缩明显，土体表面隆起现象与褶皱现象不明显。

挡墙位移实测值如表9所示。

墙后侧向水平土压力监测数据如表10所示，墙后实测侧向水平土压力分布如图14所示。

图13 单一软土模型加载前后土体变形

表9 单一软土模型挡墙位移值 单位：mm

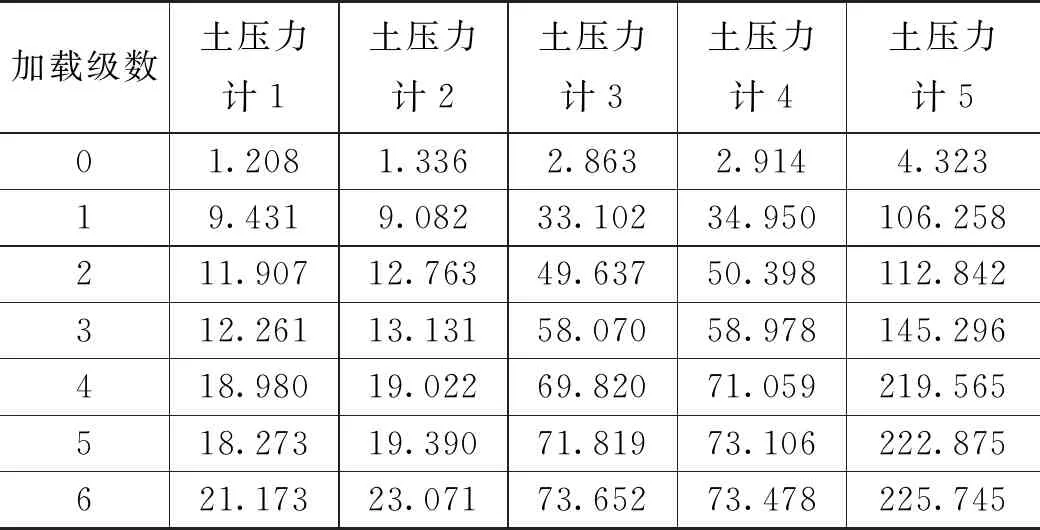
表10 单一软土模型土压力监测数据 单位：kPa

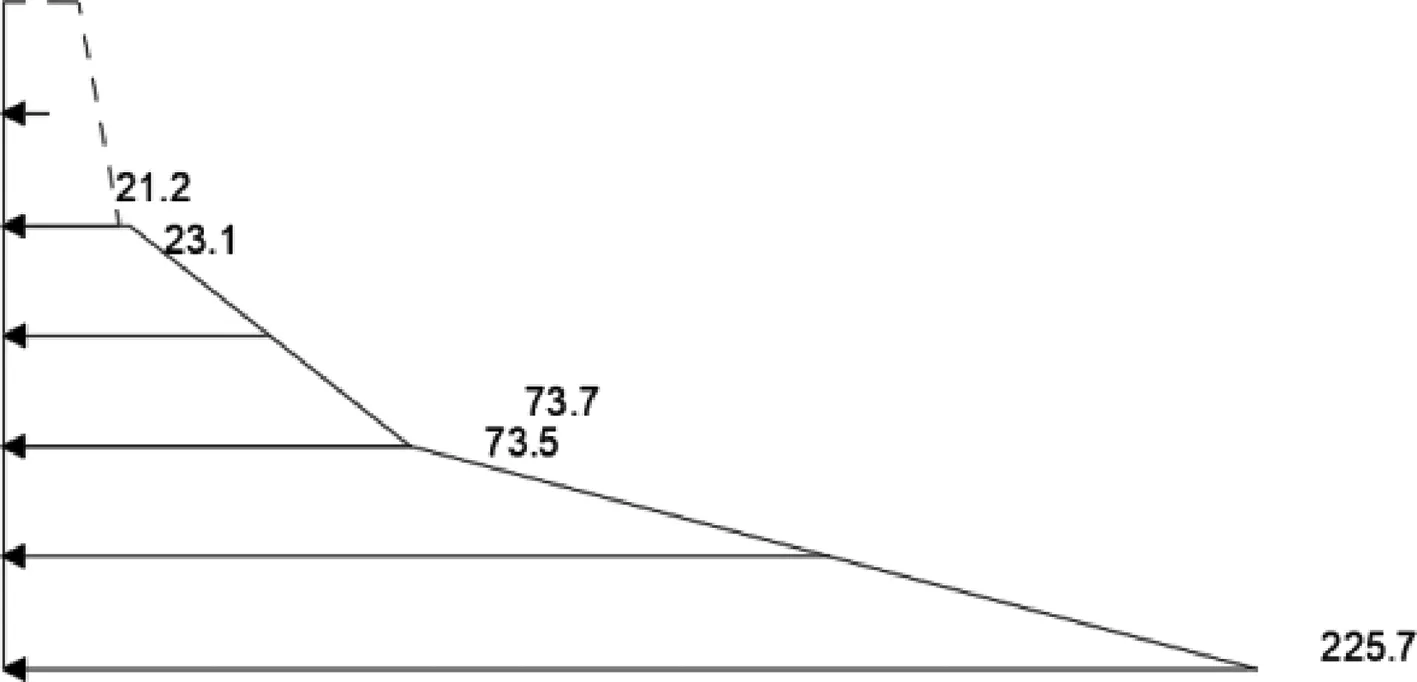
图14 单一软土模型实测土压力分布图

由表9的数据和图14可知，对于单一软土模型，土层交界处所测土压力基本相同，无突变现象产生，故仅选取土压力计1、3、5值进行分析。图15为单一软土模型土中侧向水平土压力随墙底位移变化曲线。由图15中的曲线可知，加载至第4级荷载后，继续加载，侧向水平土压力值不再增加，表明土体在第4级加载后已达到极限抗剪强度，土体剪切破坏，底部土压力增长远快于挡墙中上部，底部土层承担较大的外加荷载。

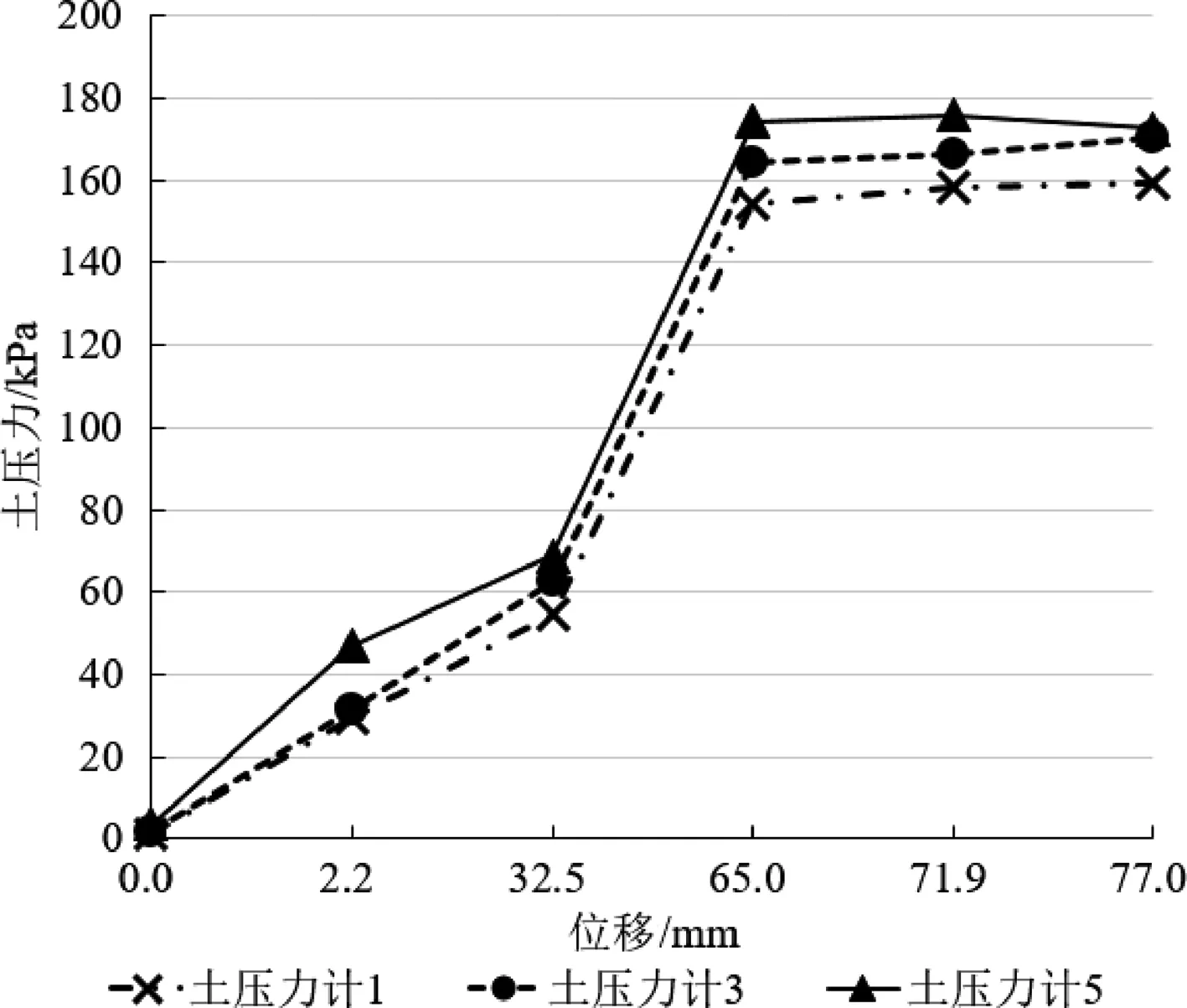
图15 单一软土模型土压力随墙底位移变化曲线

2.5 实测土压力与理论计算值比较分析

朗肯被动土压力理论计算值如表11所示，图16为非均质模型侧向水平土压力理论值与实测值对比图。

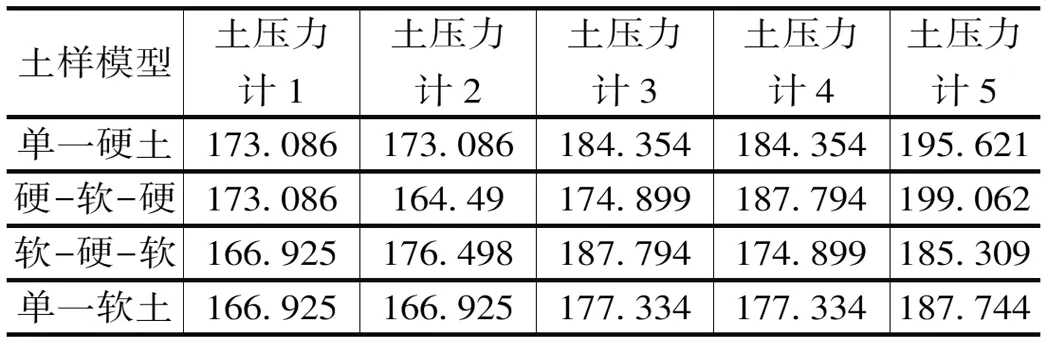
表11 挡墙墙后侧向水平被动土压力理论值 单位：kPa

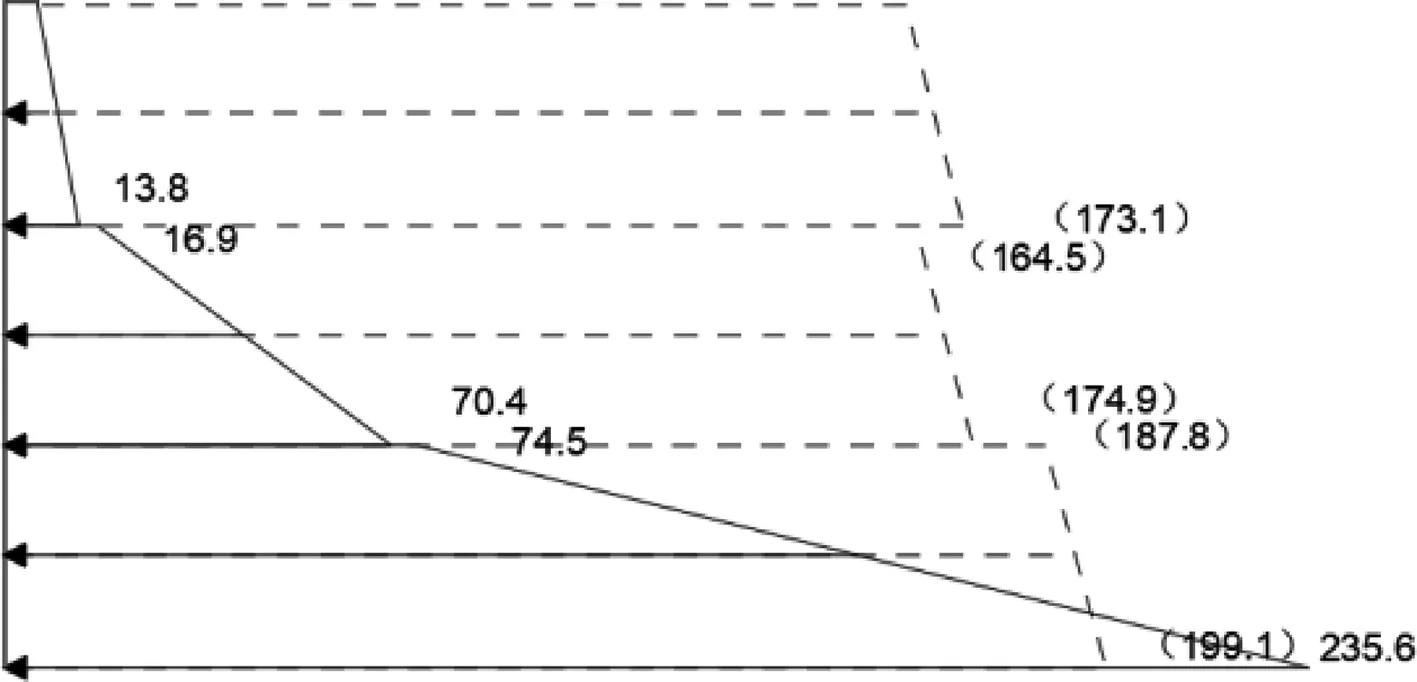
图16 硬土-软土-硬土模型实测值与理论值对比

由图16可知，挡墙下部土压力增长极为迅速，上部土土压力增长缓慢。随着逐级加载，挡墙底部实测土压力超过理论值，该处土体已被剪切破坏。然而，上部土体实测土压力值远低于理论值。这表明，挡墙绕顶转动模式，墙后水平侧向土压力分布规律不再符合平移模式理论土压力分布，底部土体已破坏，而上部土体远未达到极限平衡状态，但也存在局部屈服塑性区，土中应力状态发生改变。墙后土压力分布从土体上部往下部呈凹曲线迅速增大。软硬土层分界处土应力突变不明显。

3 结语

本文通过自制试验模型系统，开展了单一硬土、硬土-软土-硬土、软土-硬土-软土和单一软土4组模型挡墙绕顶转动室内模型试验，分析了墙后实测侧向水平土压力分布规律，并与理论值进行了对比研究，主要结论如下。

(1)挡墙绕顶转动，墙后实测被动土压力值，土体上部土压力值远小于土体下部；随着倾角增大，墙后底部土压力迅速增长，下部土体很快达到极限平衡状态而破坏；上部土体则远未达到极限平衡状态，但土体内已存在局部塑性破坏，土中应力状态发生改变。

(2)挡墙绕顶转动，墙后实测侧向水平土压力分布不再符合平移模式理论土压力分布规律，上部土层被动土压力实测值远小于理论计算值，墙后被动土压力分布图呈凹曲线分布。该模式下土压力计算理论需要进一步研究。

(3)挡墙绕顶转动，软硬土层分界处土应力突变不明显，与挡墙平动模式存在显著区别，该模式下土中应力重分布存在特殊规律。