基于双重低秩分解的不完整多视图子空间学习

徐光生，王士同

（1.江南大学 人工智能与计算机学院，江苏 无锡 214122;2.江南大学 江苏省媒体设计与软件技术重点实验室，江苏 无锡 214122）

近年来，多视图[1-2]数据分析已经引起了越来 越广泛的关注，由于科技的发展，不同类型的传感器可以从多个角度采集数据，这为我们提供了丰富的样本。但是，随之也带来了相关挑战，多视图数据中的同一类标签往往对应多个不同的样本，甚至是异构的。这导致了一个学习困难的问题，若多视图的类内数据相似性低于同一视图不同类之间的相似性，将会导致算法效果较差甚至失败。一般来说，多视图数据分析可采用3 种策略：1）特征自适应算法[3-4]，旨在寻找一个公共空间，不同视图之间的特征可以在该空间中很好地对齐；2）分类器自适应算法[5]，旨在获得适用不同的视图的分类器；3）深度学习算法[6-7]，旨在构建层次结构以捕获更多区分性特征以减轻视图分歧。本文主要采用特征自适应策略来寻找不同视图之间共享的低秩子空间。

在特征自适应方面，子空间学习[8-9]成为较热的研究热点，并在许多领域得到了广泛的运用。具体而言，子空间学习本质上是试图找到一个合适的子空间，在该子空间中尽可能地保留原始特征的区分性表示。子空间学习被引入多视图数据分析中以减轻不同视图之间的特征差异，通过常规子空间学习方法获得公共特征空间，可以解决维数诅咒和不同视图之间分布差异的问题。

低秩约束[10]已经在数据表示中被广泛采用，它最初通过找到最低秩表示并检测噪声或离群值来帮助发现数据的多个结构。因此，Zhang 等[11]采用了双重低秩分解来处理大量损坏的数据情况，但是他们只是将数据在原始的高维空间中进行低秩分解，并没有考虑到多视图之间的类结构信息与视图结构信息。此外，低秩约束被集成到子空间学习框架中以帮助处理高维数据，多视图数据的投影子空间结构可以通过低秩约束的感知位置重构特性被挖掘，从而达到减轻不同视图之间的差异的效果。

当数据在恢复底层结构方面受到限制时，从不足的观测数据中挖掘潜在的知识就变得很必要。潜在因子[12-14]在许多数据挖掘和机器学习应用场景中起着关键作用，它通过使用贪婪搜索、推断或近似算法试图寻找一些人或机器无法观测到的隐藏变量。在本文中，潜在因子被引入双重低秩分解子空间学习框架中以帮助恢复视图数据中丢失的信息，这与传统的多视图数据分析方法区分开来。

一般来说，对于常规的多视图数据分析算法，它们关注的核心问题是如何在数据分析过程中尽量减小不同视图之间的差异，这导致它们大都需要一个必要的前提条件：在训练阶段需要完整的视图信息参与算法的训练。然而，当多视图数据不完整[15]时，这些常规的多视图数据分析算法则效果较差甚至失败。不幸的是，许多现实应用场景条件苛刻，例如本文关注的不完整多视图问题，它的视图信息就是残缺的。常规的多视图数据分析算法无法很好地解决该问题，幸运的是，Liu 等[16]提出可以通过潜在因子来帮助修复不完整的视图信息，这为本文的不完整多视图问题提供了一个很好的解决思路。

为了克服上述挑战，本文提出了一种基于双重低秩分解的不完整多视图子空间学习算法(incomplete multi-view subspace learning through dual low-rank decompositions，IMSL)，所提算法可以解决不完整多视图问题。算法的主要思想是基于双重低秩[17]分解子空间学习框架，引入潜在因子修复丢失的信息。此外，本文通过预先学习多视图数据的低维特征来有效地促进视图之间的特征对齐。本文的主要贡献总结可以归纳如下：

1) 基于双重低秩分解多视图子空间学习框架，引入潜在因子以解决不完整多视图问题，并以有监督的方式来指导双重低秩分解。

2)通过预先学习多视图数据的低维特征来促进不同视图之间的特征对齐，保证算法具有更好的鲁棒性。

3)在人脸识别、物体分类等数据集上，大量的实验验证了所提算法的有效性，相较于传统的多视图学习算法有明显优势。

1 不完整多视图子空间学习

1.1 问题形式化

在不完整多视图数据分析场景下，给定多视图数据X=[X1X2···Xm]，每个视图Xi∈Rd×ni,这里一共有m个视图，其中d是原始特征维数，ni代表单个视图中的样本数量。多视图数据共包括C类样本，但单个视图并不包含所有类别样本，不同视图数据之间具有分布差异。因此，只是单纯地对多视图进行低秩分解解析结构信息并不足以帮助我们取得较好的实验效果，还需要意识到丢失信息的重要性。所以本文基于双重低秩分解子空间学习框架，引入潜在因子挖掘丢失的视图信息，致力于寻找多视图数据的共享子空间来传递视图数据中的判别性区分能力并减轻不同视图之间的分布差异。如图1 所示，相同的颜色表示数据同类别，相同的形状表示数据同视图，所提算法通过不完整多视图对齐预先学习多视图数据的低维特征，并通过施加潜在因子的双重低秩分解将视图结构与类别结构彼此分开。

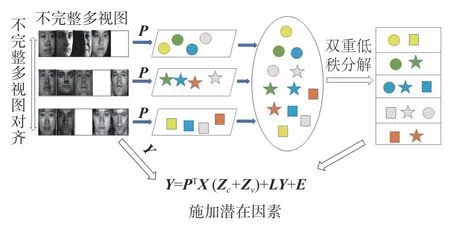
图1 本文的算法框架Fig.1 Algorithm framework of this paper

1.2 不完整多视图对齐

多视图数据分析中，不同视图由于不同来源可能具有不同的分布，为了保证它们可以传递有效的知识，将它们进行特征对齐[18]是非常必要的。此外，预先学习数据的低维特征将在算法迭代过程中保持固定，这提高了算法的鲁棒性。假设Yi∈Rp×ni是每个视图预先学习到的低维特征，Y=[Y1Y2···Ym]∈Rp×n这里p表示降维后的低维特征的维度。本文通过拉普拉斯矩阵[19]来进行多视图的特征对齐并获得它们的低维特征表示，具体细节为

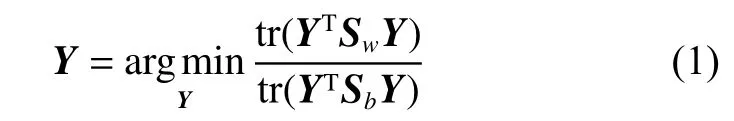
这里Sw∈Rn×n与Sb∈Rn×n分别代表多视图数据的类内拉普拉斯矩阵与类间拉普拉斯矩阵。本文旨在预先学习低维特征的过程中尽量保留更多的类内信息而尽量增大类间的差异，具体的拉普拉斯矩阵定义为

式中：υ是Sw相对于Sb的特征值；Y是最小的p个特征值所对应的特征向量。预先学习的低维特征可以在低维空间中减轻原始空间中多视图的分布散度。

1.3 基于双重低秩分解的子空间学习

在不完整多视图问题中，如何恢复丢失部分的视图信息是我们解决该问题的重点。为了恢复丢失部分的视图信息，本文首先假定丢失部分的视图信息是可观测的，因此多视图数据可以定义为X=[XO,XU]，XO为保留的视图信息，XU为丢失的视图信息。因此，针对多视图数据，引入低秩约束子空间学习公式：

式中：rank(·)代表矩阵的秩；Z∈Rn×n代表多视图的低秩重构系数矩阵，这可以帮助指导多视图的局部位置感知重建。众所周知，秩最小化问题[20]为非收敛性问题，Liu等[16]利用凸替代来解决该问题，即核范数。因此，式(3)可被重新定义为

式(6)与常规的低秩约束子空间学习相比，引入潜在因子以处理不完整多视图问题。从几何角度分析，式(6)实际上提出了通过列重构[21]与行重构[18]来重构低维视图特征，列重构通常被认为是字典学习，行重构则被称为潜在因子。在数据矩阵中，列空间代表主要特征，行空间代表关键对象部分，当数据中的某些样本丢失（即数据矩阵中的某些列为空），通过行重构来恢复数据是非常行之有效的。

然而，潜在因子只能够帮助我们恢复丢失的视图信息，而对于多类别的多视图数据，若同一类别的不同视图特征差异较大，这将导致低秩约束Z无法揭示类结构信息。实际上，多视图数据包含类结构和视图差异结构，类结构旨在揭示类信息的全局结构，视图差异结构旨在保留不同类之间的视图信息，两种独立的结构相互交织在一起。因此，Z可被分解为两个低秩部分[22]，即

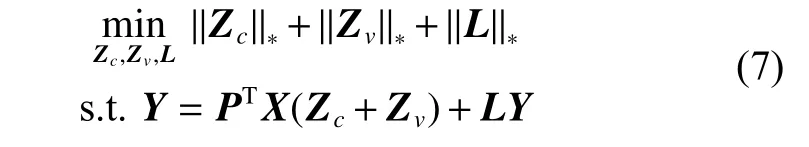
这里Zc∈Rn×n代表的是类结构的低秩表示，Zv∈Rn×n代表的是视图差异结构的低秩表示。由式(7)可知，低秩约束Z被分解为Zc和Zv，这样类结构信息和视图差异结构信息被彼此分离，避免了较大的视图差异影响类信息的全局结构。此外，为了放松原始问题，本文将稀疏项E∈Rp×n引入目标函数，将原本的硬约束转换为软约束，避免了潜在的过拟合问题。至此，目标函数可被归纳为

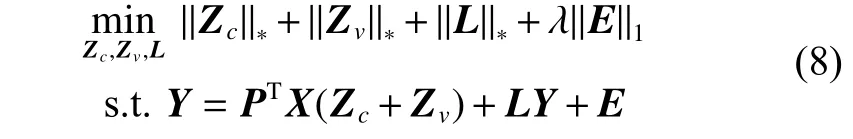
式中 ‖·‖1表示矩阵的1 范数。这里，我们只是采用无监督的方式来指导多视图的双重低秩分解。但是，无监督的方式无法将类结构信息与视图差异结构信息完全地剥离开来，因此有必要利用多视图的标签信息来完成双重低秩分解。

1.4 监督信息对齐

在不完整多视图问题中，本文期望通过有监督的方式将相互交织在一起的类结构信息与视图差异结构信息分离开来，因此针对类结构与视图差异结构，本文定义了两个监督图正则化项以此来指导多视图的双重低秩分解。假设类结构的低维特征Yc=PTXZc，视图差异结构的低维特征Yv=PTXZv，本文旨在最小化类内相似性的同时最大化视图间的差异性，以此来保留更多的类内信息并消除视图差异的影响。具体的正则化项定义为

这里，li、lj分别是xi与xj的标签信息，xi∈Nk1(xj)表示xi属于同类别的xj的k1个最近邻居集合，xi∈Nk2(xj)表示xi属于同视图的xj的k2个最近邻居集合。至此，本文采用类似LDA函数的形式来统一式(9)以求最小化类内方差且最大化同视图，但不同类的边际分布差异，其具体形式为

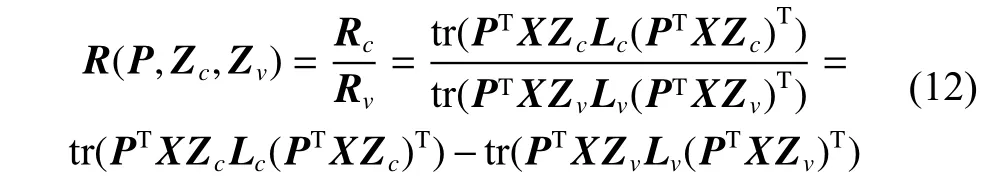
式中Lc、Lv分别是Wc和Wv的拉普拉斯矩阵。由此，同一类中的局部流形结构得以保留，且减轻了视图流形的影响。

1.5 目标函数和优化

至此，有监督的双重低秩分解可以将相互交织在一起的多视图数据中的类结构与视图结构分离开来，而在此双重低秩分解下学习到的健壮子空间使类内数据更加紧凑，同时最大化同一视图内不同类别的数据之间的边际分布差异。因此，基于双重低秩分解的不完整多视图子空间学习的目标函数可以被定义为

式中：Y1、Y2、Y3和Y4是 4 个拉格朗日乘子；µ ＞0是惩罚参数；〈〉表示矩阵的内积，即〈A,B〉=tr(ATB)。我们无法同时更新优化Jc、Jv、Zc、Zv、L、K、E和P，幸运的是，我们可以通过交替方向乘子法(altermating direction method of multipliers,ADMM)依次地解决每个子问题，并不断地迭代更新优化这些参数直至收敛。具体而言，当我们更新其中一个参数时，需要固定其他参数。假设当前迭代次数为t(t≥0 )，t+1次迭代具体各项的更新为

1)固定Jv、Zc、Zv、L、K、E和P，将它们视为常数项，从而得到Jc的更新公式：

3)固定Jc、Jv、Zv、L、K、E和P，将它们视为常数项，从而 Γ对Zc进行求导得：

4)固定Jc、Jv、Zc、L、K、E和P，将它们视为常数项，从而 Γ对Zv进行求导得：

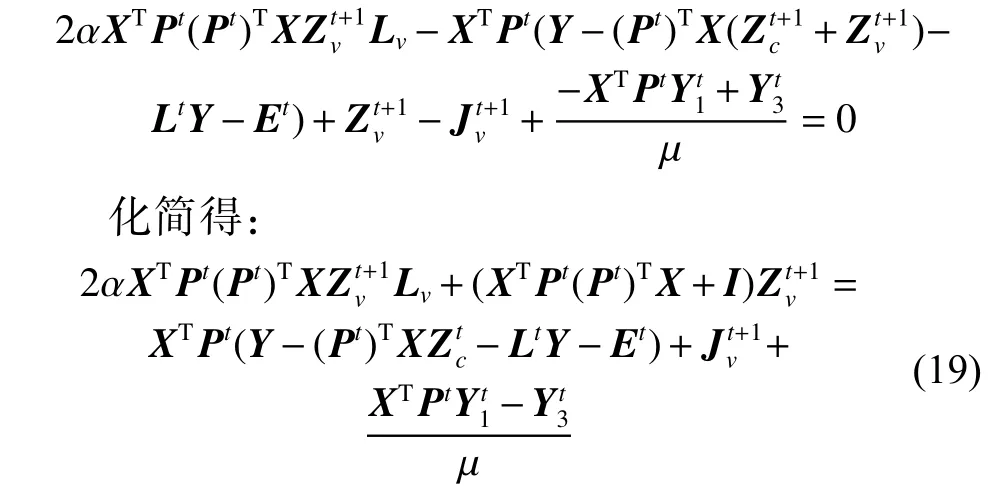
5) 固定Jc、Jv、Zc、Zv、L、E和P，将它们视为常数项，从而得到K的更新公式为

6) 固定Jc、Jv、Zc、Zv、K、E和P，将它们视为常数项，从而 Γ对L进行求导得：

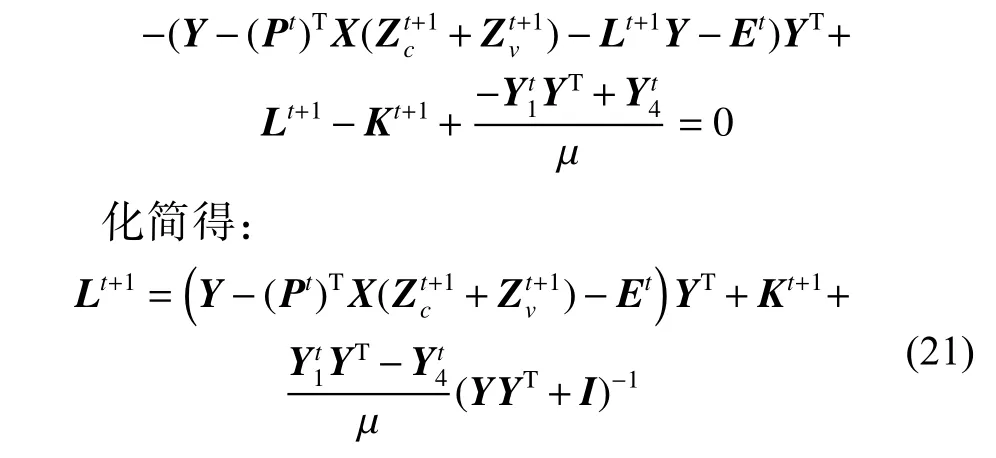
7) 固定Jc、Jv、Zc、Zv、L、K和P，将它们视为常数项，从而得到E的更新公式：

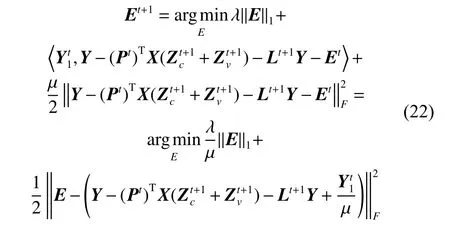
8) 固定Jc、Jv、Zc、Zv、L、K和E，将它们视为常数项，从而 Γ对P进行求导得：

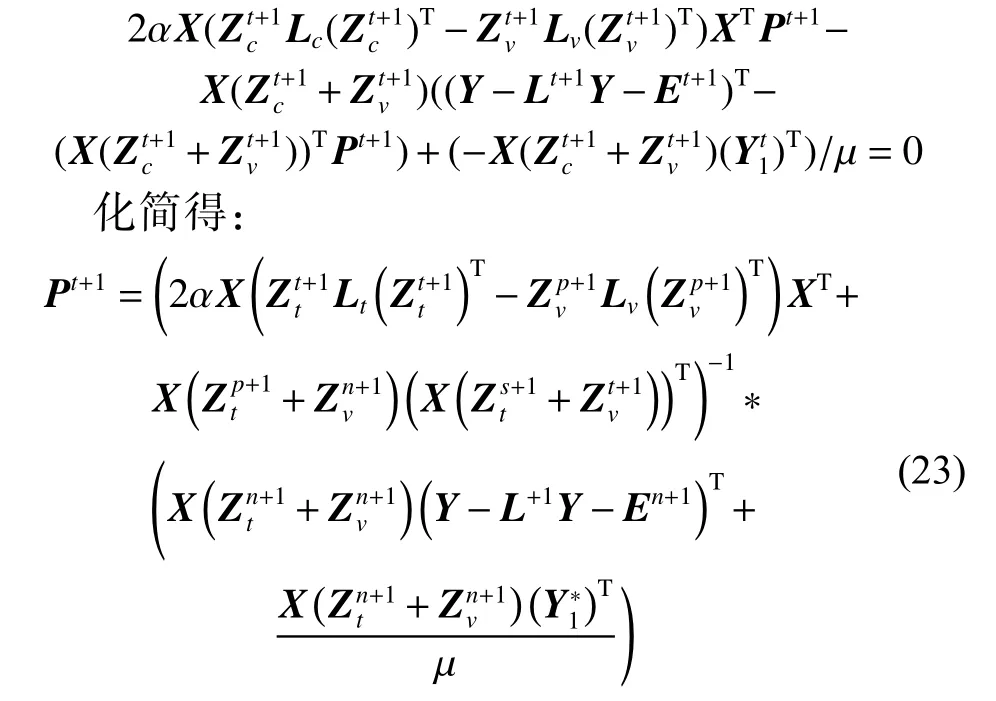
式(16)、(17)、(20)可通过奇异值阈值(SVT)运算求解得，式(18)、(19)可通过Sylvester 方程求解，式(22)可通过收缩算子进行求解，详细的算法流程在算法1中列出。参数µ、ρ、ε、µmax和tmax参考了相关的多视图分析算法RMSL[17]。其他的参数 λ、α则在实验中调节，并在实验章节中给出分析。

算法1：IMSL 的算法描述

或t达到tmax，其中 ‖·‖∞表示矩阵的无穷范数；

13)更新迭代次数t，t=t+1；

14)结束循环。

上述算法中，2)、3)、6) 的核范数计算与4)、5)、7)、9)的矩阵乘法和逆运算为主要耗时部分。2)、3) 的SVD 计算的时间复杂度为O(n3)，6) 的SVD 计算的时间复杂度为O(p3)，n为多视图的样本大小，p为降维的维数。如果在实验中选择较小的降维维数，可以加速6) 中的计算。4) 采用Sylvester 方程求解，因此主要耗时部分为矩阵乘法、逆运算和Sylvester 方程求解，可推导出其时间复杂度为O(dn2+n3)，d为原始特征维数。5) 与4)求解过程相同，时间复杂度为O(dn2+n3)。类比可以推导出7)与9)的时间复杂度分别为O(pn2+pdn)pdn)、O(dn2+nd2+d3)。8)采用收缩算子进行求解，其时间复杂度为O(pn)。通常在实验中设置p≪n且p≪d，因此综上所述，算法1 的时间复杂度为O(T(dn2+n3+d3+nd2))，T为所提算法的迭代次数。

2 实验

2.1 数据集

本文分别在3 组多视图数据集上验证了所提算法的实验效果，它们分别是人脸数据集CMUPIE、物体数据集ALOI-100 和COIL-100。

CMU-PIE 是一个多视图人脸数据集，总共有68 类样本，采取同一对象的但具有不同姿势的样本之间有着较大的差异，每个对象的每个姿势都有着21 种不同的照明变化，这里采用C05、C07、C09、C27 和C29 来构建训练集与测试集，且它们中的图像都被裁剪为32×32 的尺寸。

ALOI-100 和COIL-100 都为多视图物体数据集，都包含100 个类别物体和7 200 张图像。ALOI-100 和COIL-100 都是利用旋转角度进行采样的，因此每个类中的图像都相隔85°，共有72 张图像。本文设定4 种视图：v1 [0°,85°]、v2[90°,175°]、v3[180°,265°] 和v4[270°,355°](v 表示view)，且它们中的图像被裁剪为64×64 的尺寸。

2.2 实验设置

在实验部分，对于CMU-PIE 多视图人脸数据集，我们选取不同数量、不同姿势的视图作为数据集，从视图的每个类别中随机选择10 张图像构建训练集，剩下的图像作为测试集。而为构造不完整多视图实验场景，随机从训练集的每个视图中挑选10 个类别移除。而对于ALOI-100 和COIL-100 这两个多视图物体数据集，依次选择两个视图作为训练集，剩下的两个视图作为测试集，构建不完整多视图训练集。此外，我们使用最近邻分类器(KNN)来评估最终性能。

本文主要采用特征提取算法与多视图数据分析算法进行比较：LDA[24]、LPP[23]、LatLRR[16]、LRCS[25]、RMSL[17]和CLRS[26](CLRS1 表示施加低秩约束，CLRS2 表示未施加低秩约束)。其中，CLRS、LDA、RMSL 属于有监督的方法，LPP、LatLRR 为无监督的方法，LRCS 为弱监督方法。对于这些对比算法，同样采用最近邻分类器(KNN)来评估最终性能。

2.3 结果分析

在CMU-PIE 多视图人脸数据集上的实验结果如表1 与表2 所示，Task 1～Task 9 分别表示为{C05,C07}、{C07,C09}、{C27,C29}、{C05,C09,C27}、{C09,C27,C29}、{C05,C07,C09}、{C05,C09,C27,C29}、{C05,C07,C09,C27}、{C05,C07,C09,C27,C29}。由表1 与表2 可知，所提算法在CMU-PIE 人脸数据集的大部分测试任务中都排名第一。对于LPP 与LDA，LPP 通过热核函数来区分不同类别，LDA 通过监督信息将同类特征与异类特征加以区分，但是在不同视图之间同类特征之间存在较大差异时会导致传统的监督学习算法性能低于无监督学习算法。由表中不难看出，基于低秩约束的方法是优于传统的特征提取算法的，尤其对于有损坏的CMU-PIE 数据集，这验证了低秩约束对带有稀疏误差项的噪声有很好的抑制效果。但是相较于算法RMSL、LRCS、CLRS与IMSL，算法LatLRR 只是简单地施加低秩约束，并未考虑到在多视图场景中不同类别的特征相似性较大的可能，这导致了LatLRR 在多视图测试案例中性能较差。算法LRCS 则针对多视图场景提出学习不同视图相对应的子空间并将它们对齐，这尽可能地保留了不同视图各自的特征，但是当同类特征差异大于异类特征时则会导致该算法效果较差。算法RMSL 针对同类特征差异较大的问题提出了双重低秩分解来减小不同视图对同类别数据进行低秩分解时造成的影响，然而它对不完整多视图场景并没有一个很好的解决效果。算法CLRS 则旨在学习由各个视图特定的投影所共享的无视图低秩投影来减小视图之间的语义差距，并施加有监督的正则化项来耦合不同视图的类内数据。但是当视图数据不完整时，各个视图特定的投影所共享的特征可能趋向于非常少，这就导致最终获得的共享低秩投影性能下降。最后，算法IMSL 针对不完整多视图场景提出了引入潜在因子的双重低秩分解子空间的学习方法，潜在因子帮助挖掘丢失的视图信息，此外，预先学习的低维不完整多视图特征与监督信息对齐也进一步促进了不同视图之间的特征对齐。因此IMSL 的性能是优于以上算法的。

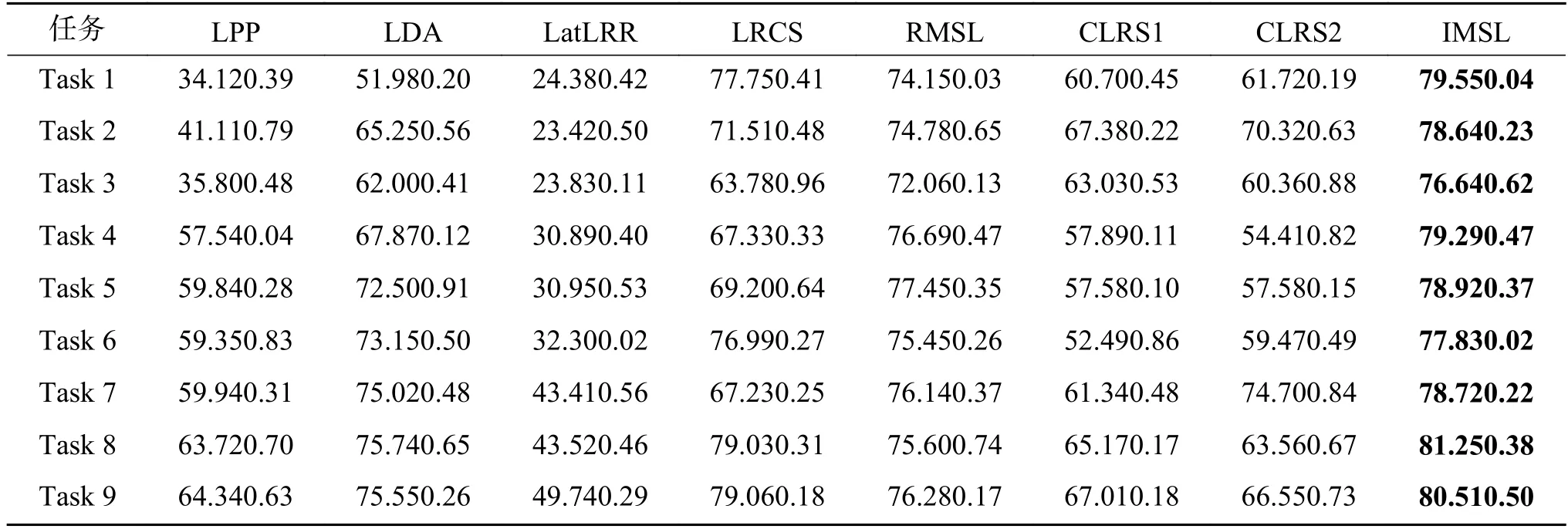
表1 在原始的CMU-PIE 人脸数据集上各算法的分类精度Table 1 Accuracy of algorithms on original CMU-PIE face datasets %

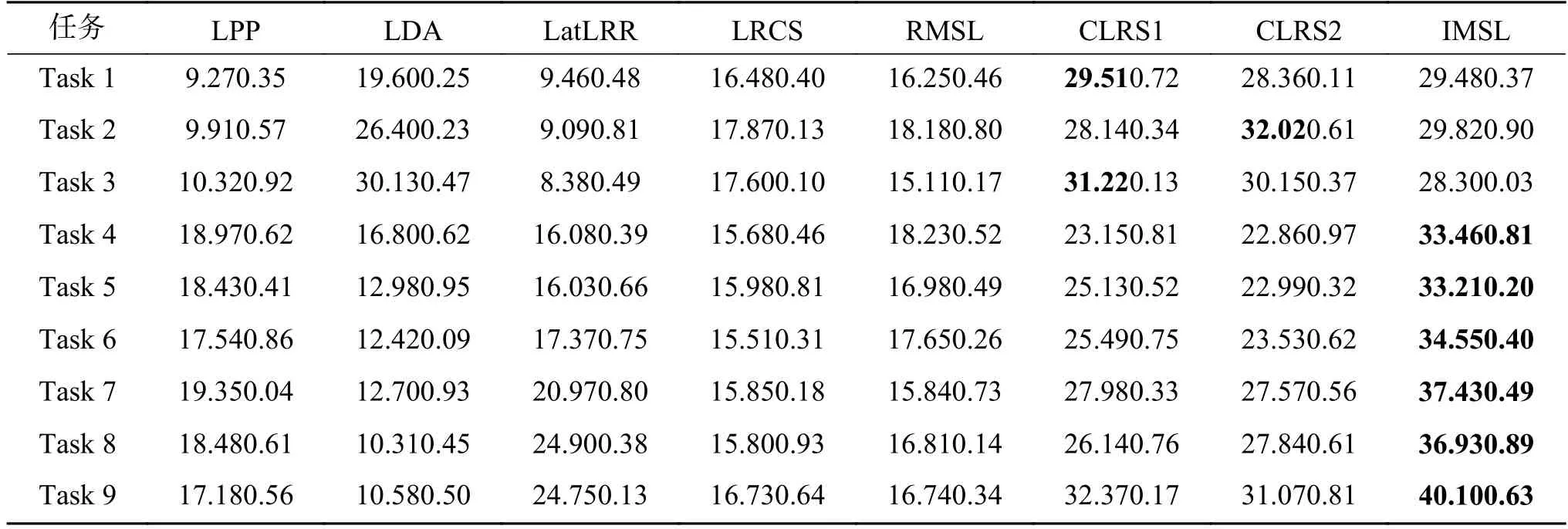
表2 在损坏的CMU-PIE 人脸数据集上各算法的分类精度Table 2 Accuracy of algorithms on corrupted CMU-PIE face datasets %

在COIL-100 多视图物体数据集上的实验结果如图2 所示，显然所提算法的平均性能在大部分测试任务中要好于所有对比算法，且受不同的视图组合影响较小。在ALOI-100 多视图物体数据集上的实验结果如图3 所示。对于不同的视图组合，所有算法的平均性能相差不大，这表明了两个视图之间的发散度在一定程度上是等效的。LRCS 与RMSL的性能较接近于所提算法，甚至LRCS 在一些测试任务中表现出更优性能，这是由于该视图组合可能同类别特征差异性较小，导致双重低秩分解的效果相较于常规的低秩分解可能较差，但是在不完整的多视图场景下，施加了潜在因子的双重低秩分解子空间学习框架仍然保证了所提算法胜任绝大多数的测试任务。

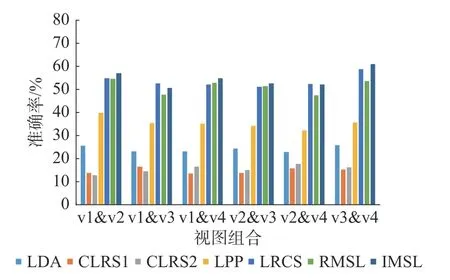
图2 在COIL-100 数据集上各算法的分类准确率Fig.2 Accuracy of algorithms on COIL-100 datasets

图3 在ALOI-100 数据集上各算法的分类准确率Fig.3 Accuracy of algorithms on ALOI-100 datasets

2.4 模型分析

本节将分析所提算法的收敛性，并评估不同子空间维度下所提算法的准确变化，此外还验证监督信息、对齐项等正则化参数的有效性。在本节中，主要评估以下参数：子空间维度参数p、稀疏项参数λ、监督信息对齐项参数 α。这里以CMUPIE 数据集作为测试案例，通过固定其他参数来逐一测试它们对于算法的意义。

图4(a)展示了以{C05 C07}作为测试案例，所提算法的准确率随迭代次数逐渐增大的变化趋势。显而易见，所提算法收敛速度较快，识别精度迅速上升并在5 次迭代后保持一个较稳定的值。

图4(b)展示以{C05C07，C05C07C09，C05C07C09C27，C05C07C09C27C29}作为测试案例，所提算法在不同子空间维度下的准确率变化。从图中不难看出，随着维度的增加，算法的精度先是逐步上升，在达到一定维度后转为平稳趋势。

图4(c)与图4(d)展示了以{C05C07，C05C07C09，C05C07C09C27，C05C07C09C27C29}为测试案例，正则化参数对所提算法准确率的影响。由图可知，当监督信息对齐项参数 α趋向于0 时算法性能较差，这验证了监督信息对齐项的有效性。稀疏项参数 λ在较小值时取得的效果较好，且随着参数值的增大算法精度趋向于稳定或一定的下降。

图4 参数分析Fig.4 Parameter analysis

3 结束语

为了解决不完整多视图问题，本文提出了一种基于双重低秩分解的不完整多视图子空间学习算法。所提算法基于双重低秩分解子空间学习框架，引入潜在因子挖掘丢失的视图信息，并通过预先学习多视图的低维特征来进行特征对齐。此外，通过监督信息来进一步地促进双重低秩分解，避免了视图结构差异对全局类结构造成的影响。在3 个数据集上的实验效果证明了所提算法的优越性。