欣赏数学之美 感悟理性精神——以苏科版数学七（下）“证明”教学为例

■吴思佳龚辉

《义务教育数学课程标准（2022年版）》指出，学生要会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。目前初中数学教学以应试为目的的现象仍然存在，教与学的目标紧紧围绕“解题”展开，基本不谈“欣赏”二字。数学的美是多方面的，有外在的形式美，也有内在的逻辑美、理性美等。在日常教学中，教师可以尝试从理性美的视角深入挖掘教材，巧妙运用素材，通过不断地引发学生思辨来引导学生欣赏数学的内在逻辑美，从而提高学生学习数学的兴趣，培养学生科学的理性精神。下面，笔者以苏科版数学七（下）“证明”为例，谈谈如何引导学生欣赏数学之美，感悟理性精神。

一、学情、教材分析

七年级学生在学习本课之前，已初步了解线段、角、三角形等简单图形的一些性质。由于大多数性质是通过实验、观察、归纳得到的，学生会受直观判断的影响，认为合情推理猜测得来的结论是正确的，缺乏严谨的数学精神和科学的思维态度。本节课是引导学生由感性认识向理性分析发展的重要转折点。教材内容虽然不多，但它对于学生深刻地理解推理证明的必要性，发展推理意识，把握说理的基本方法、形成缜密的逻辑思维是非常重要的。

二、教学目标

知晓观察、操作、实验等是认识事物的有效手段，经历一些观察、操作活动，并能对获得的数学猜想进行验证；体验直观判断不一定正确，从而能尝试从数学的角度运用已有的知识和方法寻求证据，给出证明，感受推理证明的必要性；感受数学思考的合理性和严密性，在猜想和证实数学结论的过程中，增强理性精神和推理意识。

三、教学重难点

重点：通过观察、操作、实验发现一些结论，并能通过不同的方式进行证明。难点：从数学角度运用所学知识和方法验证结论，给出证明。

四、教学片段

1.创设情境

师：请同学们观察下面几个活动并思考。

（1）取一只空玻璃杯，斜放一根筷子，慢慢向杯中注水，观察筷子发生了什么变化。

（2）你在生活中见过海市蜃楼吗？

（3）图1中，线段AB和CD长度相等吗？

图1

（4）图2中，两个阴影部分的圆一样大吗？

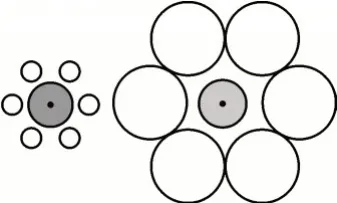
图2

（5）观察图3，AB和CD是直线吗？它们有什么特殊关系呢？

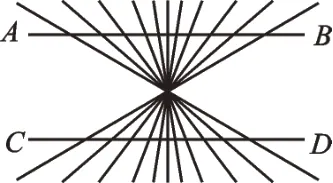
图3

（6）图4中有曲线吗？请把图5中编号相同的点用线段连接起来。

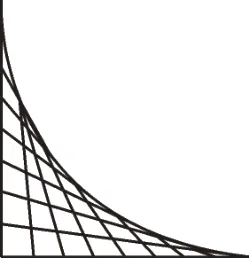
图4

图5

学生观察并讨论。

师：人们常说“耳听为虚，眼见为实”，可“眼见”真的为“实”吗？

生1：不一定。

师：刚才的例子告诉大家什么道理？生2：观察得到的结论不一定可靠。

设计意图：教师通过选取生活中的简单数学问题，开展“量一量”“比一比”等数学实验活动，激发学生强烈的思维冲突，提高学生的学习兴趣，让学生经历“眼见不一定为实”的过程，初步感受验证的必要性。

2.动手实验

活动1：奇妙的小道

师：如图6，学校的一条长为am，宽为bm的长方形草坪中间有条1m宽的笔直小道，为了增加美感，现计划改为宽恒为1m的弯曲小道（如图7）。这两条小道的面积相等吗？

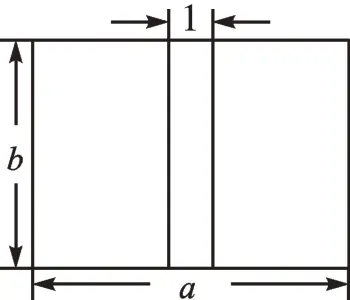
图6

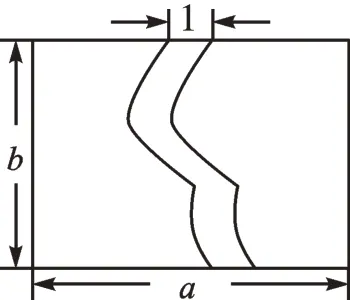
图7

生3：图7面积更大。因为弯了之后线变长，挖掉的面积会更多。

师：下结论要言之有理，你能验证吗？

生4：图6中小道的面积是bm2，图7中小道的面积却不怎么好求。

师：那怎么求出图7中小道的面积？请大家动手操作、研究一下。

生5：图6中小路的面积是bm2，图7中，可以把小道旁边的两部分平移到一起（一边操作，一边解释），所以小道的面积是ab-（a-1）bm2。

师：回答得很棒！可以平移左右两个不规则图形，把它们拼成一个整体，化简后两个代数式是一样的，都是bm2，由此证明两条小路的面积是一样的，这里体现了转化的思想。

设计意图：教师让学生经历动手操作（平移）和计算的过程，运用数学说理的方法来解决生活中的问题，发现数学的价值，培养学生应用数学的意识，增强学生学习的信心。这里用到了转化的数学思想，这是本节课的一个意外收获。

活动2：魔术的秘密

师：图8是一张8×8的正方形纸片，把它剪成4块，按图9重新拼合。这4块纸片恰好能拼成一个长为13，宽为5的长方形吗？请大家用实验手册上的纸片验证。

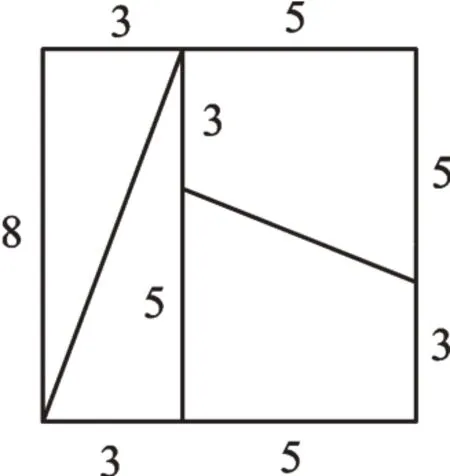
图8

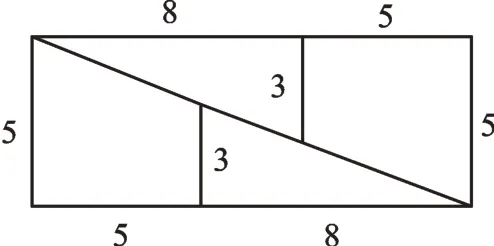
图9

学生在教师的指导下拼图。大多数学生认为能拼在一起，只有少数学生产生了质疑。

生6：我觉得是不能拼成的，因为面积不一样。图8中的面积是64，图9中的面积是65，面积增大了，不能拼在一起。

师：对。老师用几何画板演示一下（通过几何画板的演示和放大，学生看到图9中间有一条缝隙）。至于中间为什么会有一道缝，等大家到了九年级就能用说理的方式说明了。

设计意图：该活动给学生充分的时间和动手的机会，让学生在“做数学”的过程中进一步提出问题并产生思考。教师借助几何画板的演示，让学生的思维活动从直观感知上升到思辨推理，体会到实验操作得出的结论不一定正确，进一步感知了证明的必要性，培养了理性精神，同时也激发了探究新知的欲望。

3.计算猜想

活动3：探索代数式的值

师：已知代数式x2-2x+2，请回答下列问题。

（1）完成表1。

表1

（2）换几个数再试试，大胆提出你的猜想。

结论1：代数式x2-2x+2的值都是偶数。

结论2：代数式x2-2x+2的值都是正数。

师：以上结论正确吗？

生7：结论1不正确。当x=1时，代数式x2-2x+2的值为1。1是奇数，不是偶数。

师：所以，当说明一个结论不正确时，我们只要举出反例即可。那结论2呢？

生8：结论2是正确的。我代入了好几个x，发现结果都是正数。

师：你代入了几个数？你能保证代入下一个后结果还是正的吗？

生9：不能。

师：有限个数只能用来猜想。数学要“大胆猜想，小心求证”，你能说说这里的理由吗？

生10：我们可以通过配方得到（x-1）2+1，所以结果都是大于或等于1的，自然都是正数了。

师：说得太棒了。

设计意图：由特殊到一般是一种常见的解决数学问题的方法，但这并不能从根本上解决问题，所以学生就产生了如何证明的欲望。本题包含两层意思：一是要说明一个结论正确，需要经过严密的推理论证，特别是用字母表示变量时；二是要说明一个结论错误，只需要举一个反例。学生在操作交流中提升对归纳猜想、合情推理的本质认识，既获得了数学知识，又掌握了数学经验，有助于发展勇于探索的创新精神。

活动4：数学史料

教师介绍费马数和欧拉的故事（故事略）。

学生交流讨论学习感想。

设计意图：通过费马数和欧拉的故事，再次说明只凭感觉或只靠对部分例子的研究来判断一个数学结论是否正确是不够的，合乎逻辑的推理证明是必要的。同时也用数学史提升学生对数学的兴趣，培养学生的核心素养。

五、教学反思

数学来源于生活。数学课不仅要再现生活数学的美丽图景，还要带领学生走进“数”的海洋。教师创设问题情境，引导学生进行深入细致的观察分析，可以培养学生的观察能力和直觉思维能力，同时，构建数学活动可以培养学生分析问题和解决问题的能力。在教学过程中，我们既要重视直观教具的使用，还要尽可能地让学生多参加实践操作活动。动手剪、拼的过程是探索理性精神的引子，目的是让学生自然而然地产生深入研究的欲望，感受数学的严谨美和应用美，弘扬数学美的文化价值。

这就要求教师在今后的教学中，学会用欣赏的眼光去审视数学知识，深入挖掘数学内容中所蕴含的数学美，并运用巧妙的手段寓美于教，让学生怀美而学，唤起学生的审美欲望，使学生在汲取知识的同时，体会数学独特的美学价值，提高学习数学的兴趣，培养自我反思和勇于探索的理性精神。