可调数目吸引子共存的混沌系统及同步控制
颜闽秀,谢俊红
(沈阳化工大学 a.信息工程学院; b. 工业环境-资源协同控制与优化技术辽宁省高校重点实验室,沈阳 110142)
0 引言
混沌系统是随时间不可预测的系统,对初始条件和参数的变化具有极端的敏感性。混沌用于许多非线性科学领域,如信息处理、安全通信等[1-2]。最近几年,一些非线性混沌动力系统的研究成为热点。如Hyperjerk系统、多稳态、共存吸引子混沌系统等[3-5]。这些混沌系统可以分为两个主要类别:一是具有自我激发吸引子的系统类别;二是具有隐藏吸引子的系统类别。值得注意的是,有自我激发吸引子和隐藏吸引子两者都存在的系统。如何生成混沌系统是个有趣的方向。
一种是在简单的数学模型中发现非线性系统中的混沌,最具有代表性的是SprootB构造了含有五项式和两个非线性项以及六项式和一个非线性项的混沌系统[6]。另一种方法构造具有特殊奇异吸引子的混沌系统,如多涡卷吸引子、多翼吸引子等[7-8]。平衡点的个数在一定程度上决定了动力学性质。一般认为,没有平衡点的混沌系统能够产生隐藏吸引子。大量的研究表明,具有多个不稳定平衡点的混沌系统往往具有更丰富的动力学行为且更容易产生吸引子的共存。因此许多学者倾向于构造混沌系统,并通过平衡点的类型来区分动力学特性,如鞍点、不稳定焦点和其他类型平衡点的混沌系统[9-11]。
近期,混沌系统中吸引子的共存引起了学者们的广泛关注。Li等[12-13]通过数值实验研究了Lorenz混沌系统中的吸引子的共存,并提出了产生共存吸引的方法。Kengne等[14]提出了Jerk系统中吸引子的共存。Bao等[15-16]发现,基于忆阻器的混沌系统可以产生不同类型的共存吸引子。Li等[17-18]深入研究了基于忆阻器的混沌系统中的共存吸引子,并考虑将其应用在图像加密中。基于以上研究,不难发现,较传统的混沌系统,具有吸引子共存的混沌系统动态行为更加复杂,应用在同步通信中具有较好的潜力。因此,提出具有吸引子共存的混沌系统是有意义的。从建立具有简单系统和复杂行为的角度出发,提出了一个具有无限多吸引子共存的混沌系统,且将双曲正切函数加入该系统,并对该系统的动态特性进行了必要的理论和实验研究。研究表明该系统所产生的吸引子共存具有可调性,理论研究上能够产生无限多的吸引子共存。此外,将主动反推全局同步控制的方法应用在该系统中。该主动控制方法是以严格反馈设计的形式实现控制系统平衡点镇定的递推过程,反推同步控制方法广泛应用于非线性系统的控制中[19-20]。进一步,设计了反馈控制律,然后对反馈控制律进行修正,进而设计出真正的控制器,实现了系统的全局同步控制。
1 系统模型
建立系统模型为
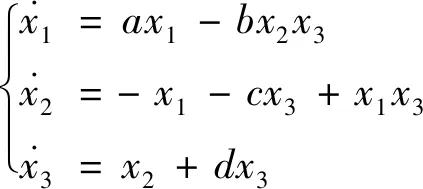
(1)
其中,x1,x2,x3为状态变量,a,b为系统常数,当a=-1.5,b=15,c=2,d=0.5时,系统(1)为混沌系统。在仿真中,将初值取为(0.1,0.1,0.1),图1展现了系统(1)的吸引子。
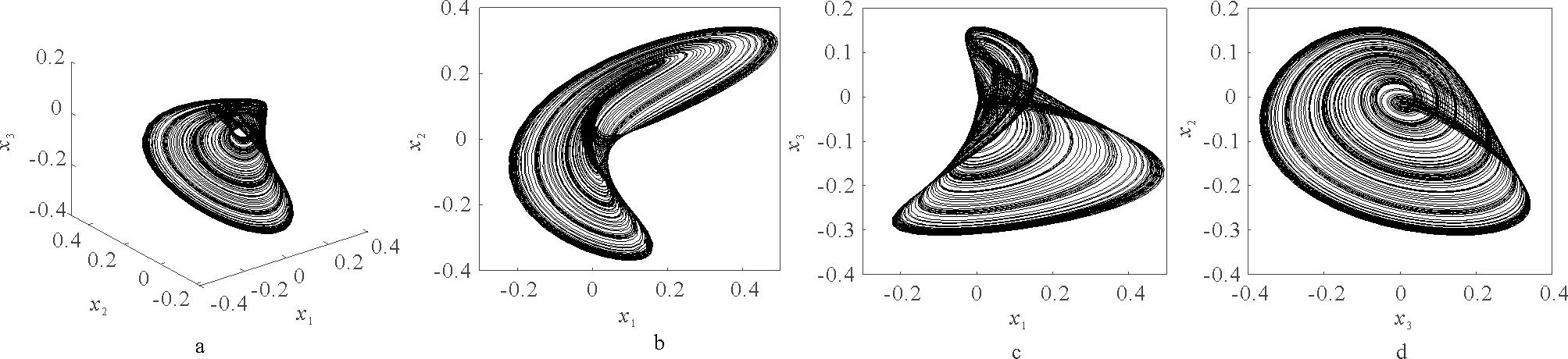
图1 系统(1)的相图Fig.1 Phase diagram of system (1)
当参数a=-1.5,b=15,c=2,d=0.5时,计算出系统(1)的李雅普诺夫指数为
L1=0.15,L2=0,L3=-1.17
(2)
通过式(2)可看出,最大李雅普诺夫指数为L1=0.15且指数之和总是为负数。
计算李雅普诺夫维数得到
(3)
其中,j满足最大整数为
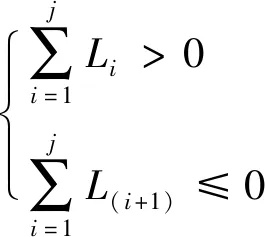
(4)
根据式(2)和式(3)看出,李雅普诺夫指数为(+,0,-)且维数为分数维,符合混沌系统的基本性质。
为了再次验证系统(1)为混沌系统,选取a作为控制参数,通过MATLAB绘制其分岔图和李雅普诺夫指数图,如图2所示。
图2展现了系统(1)在a∈[-3,-1]区间的分岔图及李雅普诺夫指数谱。图2a分岔图表明系统(1)在a∈[-3,-1]区间内系统由周期运动进入混沌运动。当a=-1.5时,图2a的分岔图中有成片的密集点且相对应的图2b的李雅普诺夫指数为(+,0,-),再次说明了系统(1)是混沌的。
系统复杂度的特性是应用在通信领域中的重要理论基础,为了验证该混沌系统的复杂行为,以谱熵(SE)为例,SE采用傅式变换并与Shannon熵进行结合得到SE的值,具体算法如下所示。
步骤1去直流。伪随机序列的长度为N,利用式(5)除掉其中直流部分,能量的信号能够被频谱更加精确地表现。

(5)
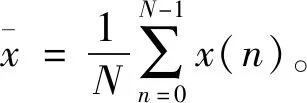
步骤2对x(n)进行离散傅式转换。
(6)
其中,k=0,1,2,…,N-1。
步骤3计算相对功率谱,依据式(6)中的X(k)序列前半部分,根据Paserval定理,计算某个特定的频率点功率谱。
(7)
其中,k=0,1,2,…,N/2-1
序列的总功率
(8)
那么,相对功率谱概率
(9)

步骤4根据式(7)、(8)和(9),并与Shannon熵进行结合,计算信号的谱熵
(10)
若PK=0,则PKlnPK=0,se的大小将在ln(N/2)处收敛,为了便于分析se,将其进行归一化处理
(11)
可见,若序列的振幅不明显,则说明结构简单,那么,所得到的谱熵值也就越小,相应地,复杂度也就越小,否则,复杂度就越大。
根据上述SE算法,对系统(1)进行了计算,并于图3展示了SE的计算结果。
图3展示了系统(1)在a∈[-3,-1]区间谱熵的复杂度,谱熵的最大测量值接近于0.7且振幅较为明显,因此,复杂度相对较高。一般地,谱熵的复杂度有明显下降时,系统为周期态,反之,系统为混沌态,该仿真实验结果与图2基本一致。
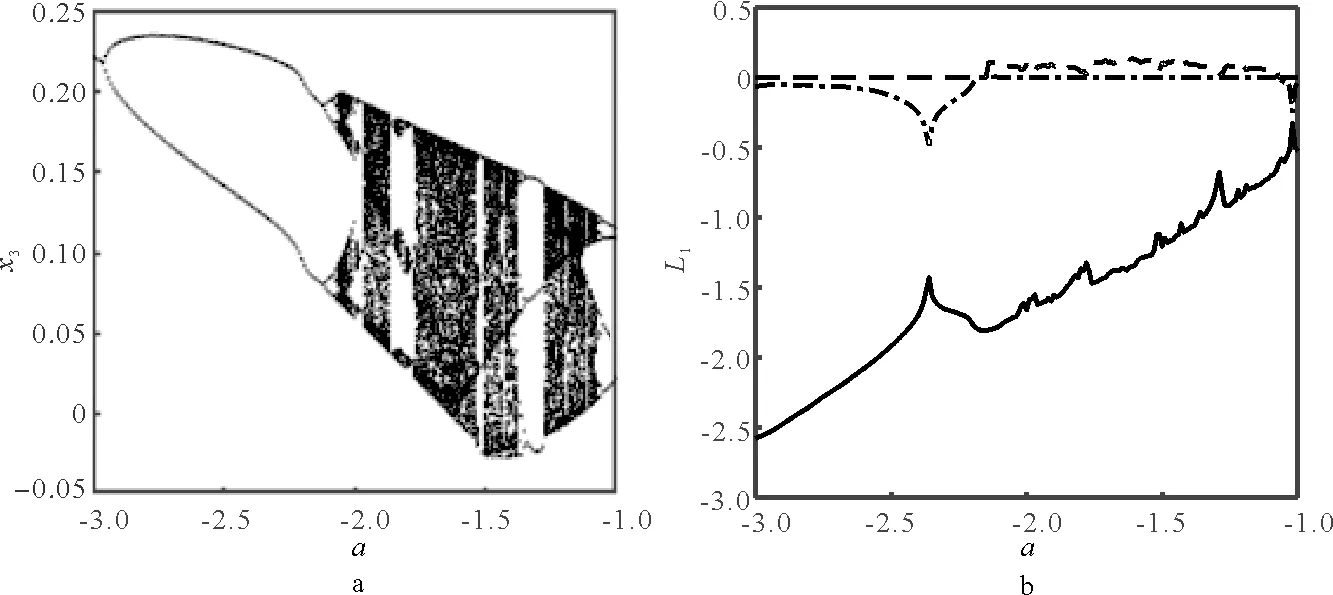
图2 系统的动态特性Fig.2 Dynamic characteristics of the system

图3 SE复杂度Fig.3 SE complexity
2 可调数目的吸引子共存
基于系统(1),为了使具有可调数目的吸引子共存,考虑建立双曲正切函数的序列用于生成具有无限吸引子共存的混沌系统,建立函数
(12)
其中,n为非负整数,参数λ可调节,此时取λ=100。可看出,随着n增大,函数θi(xi)的零点得到扩展。利用θ1(x1)取代系统(1)中等式右边的x1,那么在特定参数下,得到的新系统将会沿x1的方向产生共存吸引子。
首先,考虑沿x1轴的方向产生共存的吸引子,利用θ1(x1)取代系统(1)中等式右边的x1,得到系统

(13)
系统(1)将会沿x1的方向产生混沌吸引子的共存,如图4所示,分别给出了n=0,1时的系统(1)的吸引子共存。
图4a和b分别展示了n=0和n=1时的混沌共存吸引子,其中,图4a中的混沌共存吸引子对应的初值为(2i-3,0.1,-0.1),其中i=1,2,图4b中的混沌共存吸引子对应的初值为(2i-5,0.1,-0.1),其中i=1,2,3,4。这些混沌吸引子的共存形状相似,但是轨迹并不相同。若继续增大n,系统将会沿x1轴方向产生更多的混沌吸引子共存。
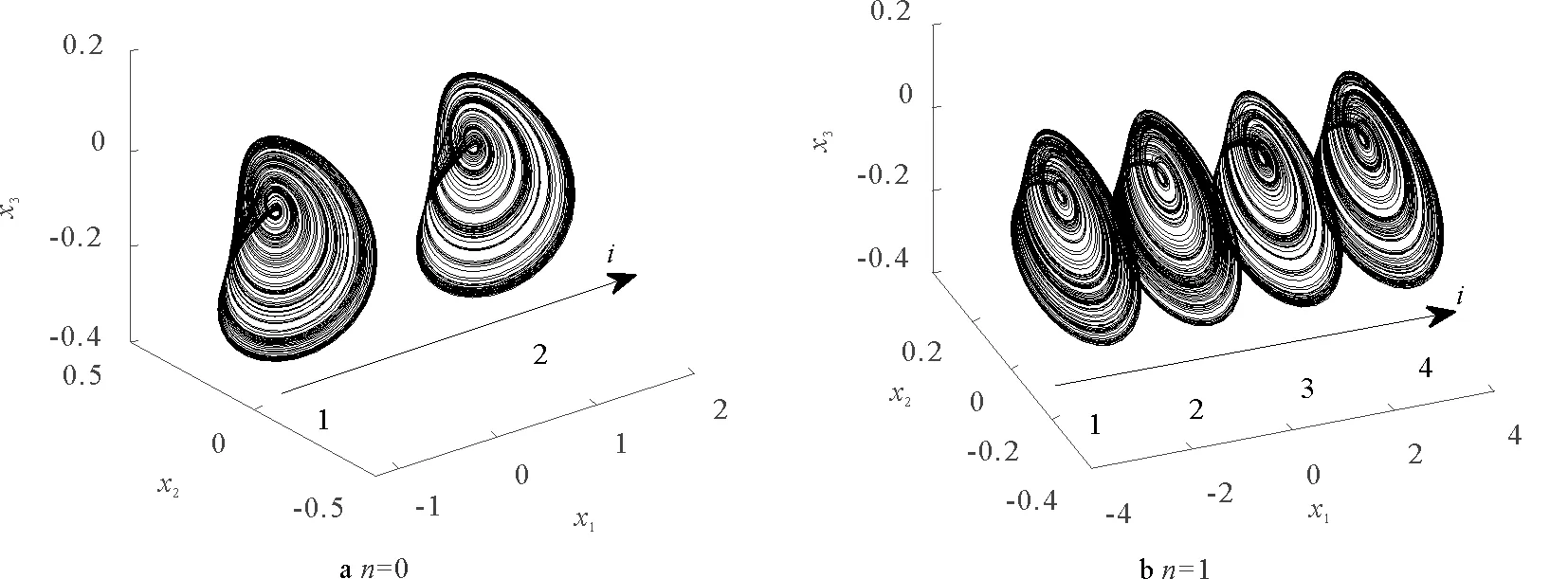
图4 混沌吸引子共存 Fig.4 Coexistence of chaotic attractors
其次,考虑用H2(x2)取代系统(13)中等式右边的x2,得到系统(14)

(14)
系统(14)将会沿x1和x2轴方向产生共存的混沌吸引子,图5分别给出了参数n=0,1时的吸引子。
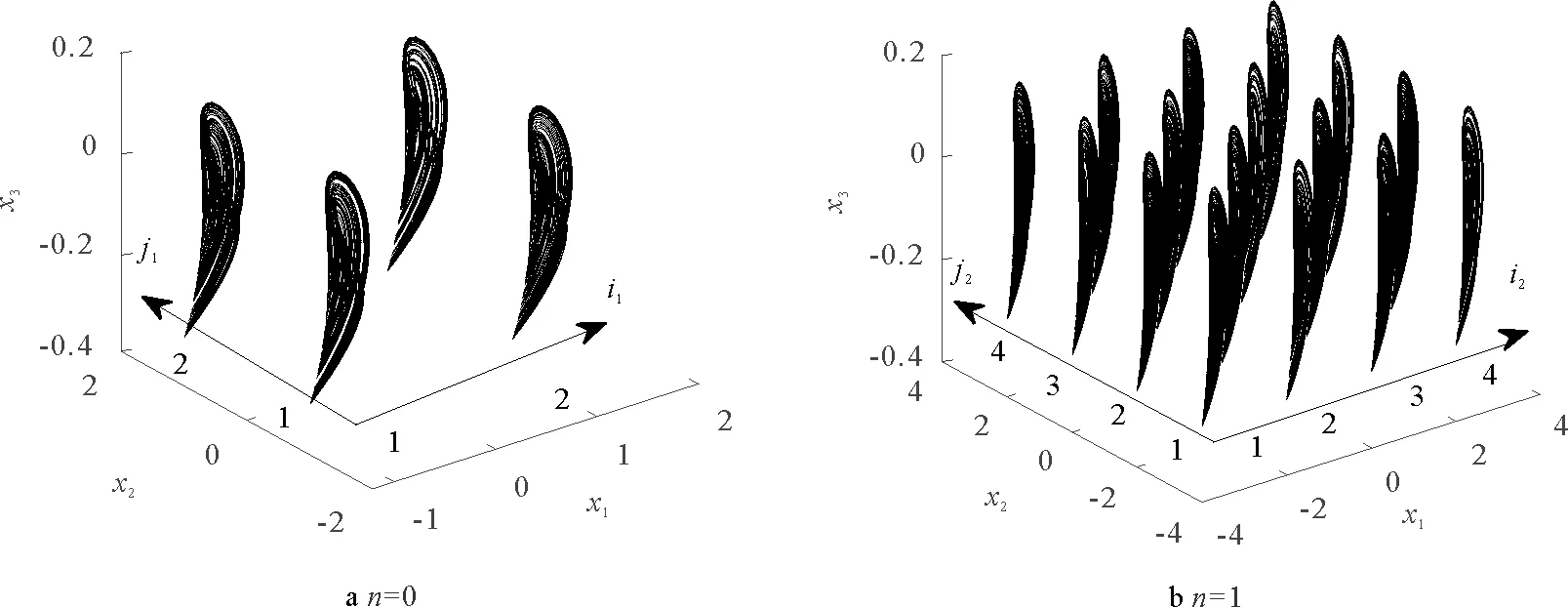
图5 x1和x2轴上的吸引子共存 Fig.5 Coexistence of attractors on x1 and x2 axes
图5a和b分别展示了2×2,4×4的吸引子,这些吸引子对应的初始条件分别为(2i1-3,2j1-3,-0.1),(2i2-5,2j2-5,-0.1),其中,i1,j1=1,2,i2,j2=1,2,3,4。
最后,考虑用H3(x3)取代系统(14)中等式右边的x3,得到系统(15):
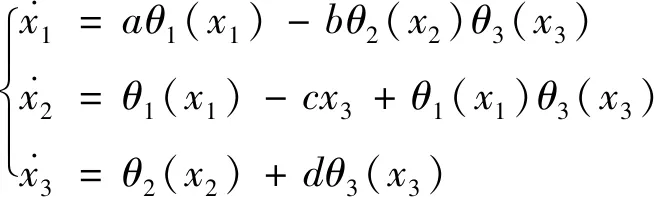
(15)
系统(15)将会沿x1、x2和x3轴方向产生共存的混沌吸引子,图6分别给出了当n=0,1时的系统(15)的吸引子。
图6a和b分别展示了2×2×2,4×4×4的吸引子,它们所对应的初始值分别为(2i1-3,2j1-3,2k1-2.8),(2i2-5,2j2-5,2k2-4.8),其中,i1,j1,k1=1,2,i2,j2,k2=1,2,3,4。

图6 x1、x2和x3轴方向上的吸引子共存Fig.6 Coexistence of attractors on x1,x2 and x3axes
通过上述研究表明,系统(1)在函数(12)的作用下,通过调整n可以改变吸引子共存的生成个数。通常,若沿r个方向来产生吸引子的共存,系统(13)(14)(15)生成的吸引子共存个数至少为Nr=(2n+2)r,r=1,2,3。当n→∞,Nr→∞时,即吸引子共存个数趋近于无限多个。
3 混沌系统的主动反推全局同步控制
反推控制的设计方法是针对不确定系统的一种系统化的控制器综合方法,它能够应用在线性系统与非线性系统中。特别地,应用在非线性复杂系统中时,它能使在线计算时间的目的减少,同时,通过设计反推使得V函数和控制器的设计过程系统化及结构化。
这里,基于含有双曲正切函数的系统(14),采用主动反推同步控制的方法用于实现非线性复杂系统的同步控制。
选取系统(14)为驱动系统,如式(16):

(16)
其中,x1,x2,x3为状态变量,a,b,c,d为系统的参数。
相应的响应系统如式(17):
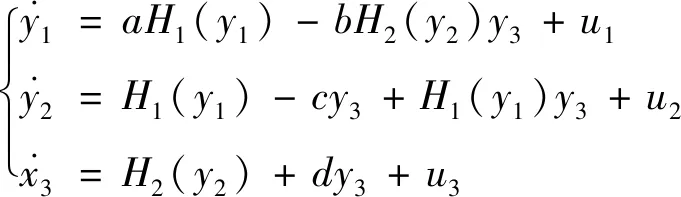
(17)
其中,yi为状态变量,ui是反馈控制律,i=1,2,3。
系统(16)和系统(17)之间的同步误差定义为
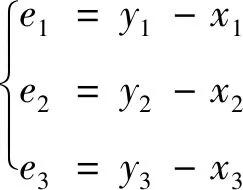
(18)
同步误差系统为
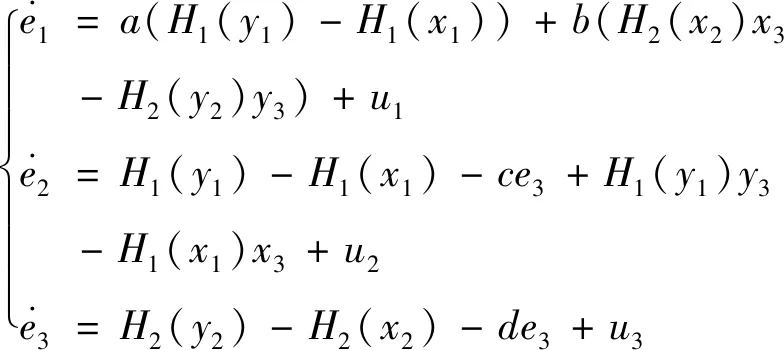
(19)
考虑设计反馈制律为

(20)
将式(20)代入式(19),误差系统简化为
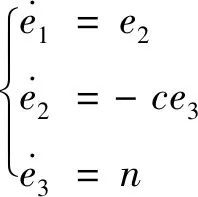
(21)
选取李雅普诺夫函数为
(22)
其中,
θ1=e1
(23)
对式(22)进行求导得到
(24)
其中,令:
θ2=e1+e2
(25)
简化式(24)为
(26)
接下来,选取李雅普诺夫函数为
(27)
进行求导得到
(28)
同理,
(29)
经过反推得到
(30)
令n=-3e1-5e2-3e3-kθ3,得到
N=-kθ3
(31)
将式(30)代入式(29)得到
(32)
其中,它在R6上是半正定和二次的函数。
根据李雅普诺夫稳定性理论可知, 当t→∞时,全部的ei(0)∈R,(i=1,2,3),误差系统ei(t)→0,(i=1,2,3)。误差系统全局渐近稳定,驱动与响应系统实现全局同步。
最后,将反馈控制律更新为
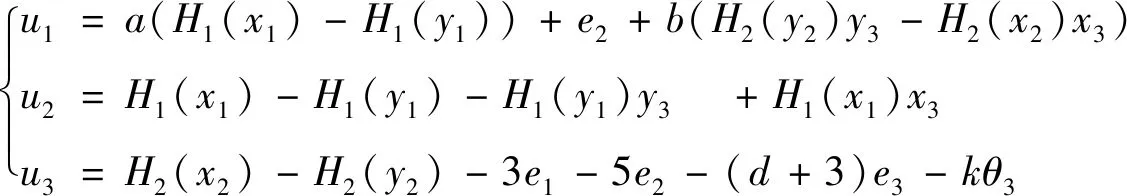
(33)

图7 系统(16)和(17)误差同步Fig.7 Error synchronization of system (16) and (17)
其中,k为控制增益,k>0,控制增益k取值越大,同步误差收敛于零的速度越快,所需要的时间就越短。如图7所示,系统(16)和(17)实现误差同步。
数值仿真实验时,选择参数(a,b,c,d)=(1.5,15,2,0.5),控制增益k=20,初值驱动系统X(0)=(0.1,0.1,0.1)和响应初值Y(0)=(5.8,-4.9,-1)。
图7表明误差同步在较短的时间内收敛于零。数值分析和实验结果一致。验证了该方法的有效性。
4 结论和展望
本文提出了一种模型较为简单的混沌系统。描述了该系统的基本特性,为能够生成混沌吸引子提供了基础。进一步地,将双曲正切函数加入该系统,使得该系统能够产生无限多吸引子共存且吸引子的个数具有可调性。理论研究表明该系统能够生成无限多个吸引子的共存,为生成无限多吸引子共存的混沌系统提供了理论依据。此外,在含有双曲正切函数系统的基础上设计了反馈控制律及系统的控制器,实现了系统的全局同步控制。理论研究和数值模拟仿真验证了主要研究结果。该系统具有无限多个可调数目的吸引子共存,与传统混沌系统相比其动力学行为更复杂。下一步计划将其应用在安全通信中。

