双高频方波注入法双绕组永磁同步电机无位置传感器控制
周奇勋,马平安,周勇,贺虎成,畅冲冲
(1.西安科技大学 电气与控制工程学院,陕西 西安 710054;2.西北工业大学 航空学院,陕西 西安 710072;3.易事特集团股份有限公司,广东 东莞 523808)
双绕组永磁同步电机(dual-winding permanent magnet synchronous motor,DW-PMSM)相较于传统的三相永磁同步电机具有更高可靠性、更优异的容错性能,被广泛应用于航空航天、舰船、汽车等领域[1-3]。DW-PMSM控制需要获取转子位置信息,采用机械式转子位置传感器不仅会增加成本,还会增加电机体积,限制了DW-PMSM的进一步应用[4-6]。因此,无位置传感器控制技术一直是研究热点之一。
在DW-PMSM无位置传感器控制中,估计电机零低速运行状态下转子位置信息,常采用的方法为高频方波注入法[7](high frequency square wave injection,HFSWI),该方法能够充分利用电机的凸极性追踪转子位置[8-9],它不依赖于电机的参数信息,且位置估计效果好[10]。但是,HFSWI会带来额外的高频转矩脉动,产生严重的高频噪声[11-12]。文献[13]提出了一种采用二次电流差分的位置信号解调法,并且为了抑制高频纹波,提出了一种基于二次差值法的滤波观测器,该方法有效减小了高频噪声,但是计算量加大,增加了处理器的负担。文献[3]针对DW-PMSM提出了一种零序电压的脉动载波信号注入的方法,通过2个注入的高频信号的相移抑制不良谐波,但是需要在2个中性点间放置一个电感,降低了系统的稳定性。文献[14]提出了基于锯齿载波的双随机SVPWM控制方法,显著降低了相电流噪声幅值,但必须保证开关序列在开关周期内是中心对称的。近几年随机信号注入法[15]被提出,用于降低高频噪声,该方法基于随机脉冲宽度调制(pulse width modulation,PWM)[16-17]思想。文献[18]在五相电机控制系统中提出了随机零矢量-变延时双随机SVPWM方法,降低了高频谐波的幅值,但是随机扩频调制研究仍处于起步阶段。
针对零低速下DW-PMSM高频方波注入的无位置传感器控制系统存在的高频转矩脉动问题,本文提出了一种双高频脉冲注入法(dual high frequency square wave injection,DHFSWI),即在2套绕组同时注入高频方波的方法。通过建立永磁同步电机的高频数学模型,得出了高频脉动的表达式,分析出高频脉动产生的原因。根据同相位DW-PMSM 2套绕组的空间位置关系与同一时刻高频脉动代数和为零的原则,推导出第二套注入脉冲信号的形式。利用双绕组永磁同步电机拥有2套绕组的优势,提出了双绕组位置估计误差最小提取方法,以提高转子位置估计精度。仿真和实验结果表明,本文所提出的方法,可以消除转矩脉动,提高位置角估计精度,实现DW-PMSM无位置传感器控制。
1 高频转矩脉动分析
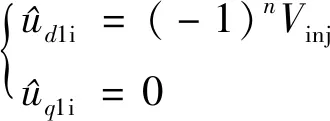
(1)
式中:Vinj为注入高频方波的幅值;n为采样序号。
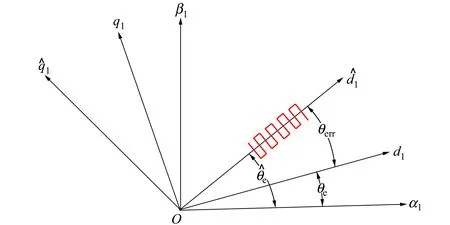
图1 HFSWI示意图
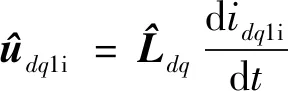
(2)
式中
(3)
(2)式可转换为
(4)
将(1)式代入(4)式可得
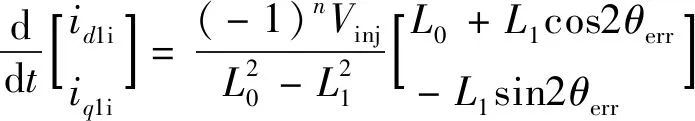
(5)
将(5)式进行离散化之后得
(6)
式中:TPWM为PWM的周期。
由(6)式可以得
(7)
针对表贴式DW-PMSM,采用id=0控制算法,DW-PMSM转矩公式[2]可以简化为
Te=1.5pn(iq1ψd1+iq2ψd2)
(8)
由(7)式和(8)式得到由高频方波注入引起的转矩脉动ΔTe为
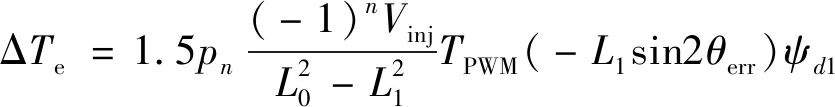
(9)
由(9)式知ΔTe不仅与注入的高频方波信号幅值有关,还与θerr有关。故不仅可以减小高频方波的幅值还可以减小转子位置角估计误差以减小ΔTe。
2 DHFSWI无位置传感器控制系统
基于DHFSWI的DW-PMSM无位置传感器控制系统原理框图如图2所示。DW-PMSM的2套绕组分别做闭环控制,其中无位置控制传感器最重要的部分为:高频信号注入、高频与基频信号分离、观测器。在第一套绕组的估计d轴注入高频方波Vinj1,第二套绕组的估计d轴注入高频方波Vinj2,分别从
2套绕组三相电流中分离出高频与基频信号,观测器通过观测高频信号得到估计的位置角。
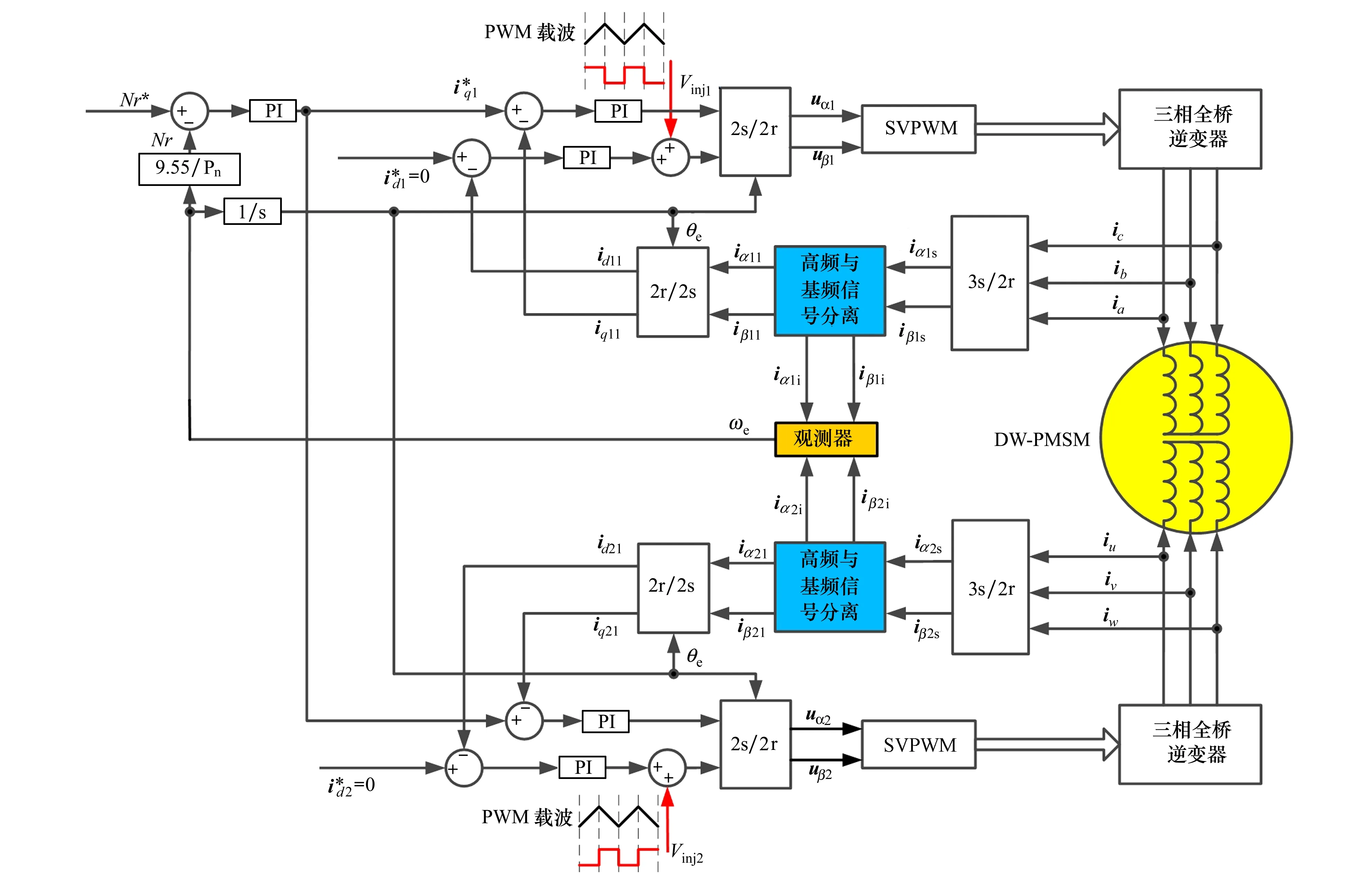
图2 基于DHFSWI的DW-PMSM无位置传感器控制系统原理框图
2.1 DW-PMSM双高频方波注入
同相位DW-PMSM 2套绕组之间的中性点隔离,2套绕组的Oαβ坐标关系以及DHFSWI注入的位置如图3所示。

图3 DHFSWI示意图
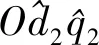
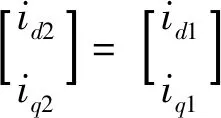
(10)
假设第二套绕组注入的高频方波脉冲为
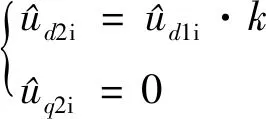
(11)
由(8)式知,令Te=0,采用id=0得到Δiq2i与Δiq1i的关系为
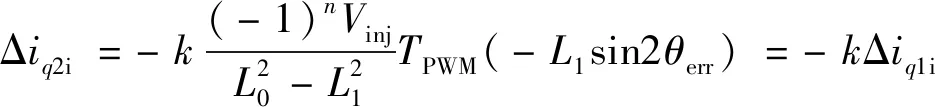
(12)
根据(10)式与(12)式得到
k=-1
(13)
因此第二套绕组注入的高频电压信号为
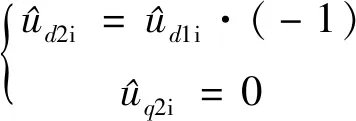
(14)
故在第一套绕组注入高频方波如(1)式,在第二套绕组注入脉冲信号如(14)式时,DW-PMSM产生的高频转矩脉动为零。
其验证流程也十分简明,客户端使用用户凭据登录系统,服务器验证通过后,依据上述规则生成jwt 返回给客户端。客户端之后在向服务器请求时,通过header 中的Authorization 字段以Bearer 形式携带此token 来发送至服务器端验证身份和权限。一般的token流程可以由图2 来表示,申请为1~2 步骤进行,请求资源以3~6 步骤进行。
2.2 位置观测器的原理与设计
位置观测器是整个DW-PMSM无位置传感器控制系统的核心部分,该部分需提取高频电流以及通过高频电流信号提取转子位置信息。
以第一套绕组为例,在某一采样时刻,电流响应为(15)式,可以使用电流差分的方法提取出含有位置信息的高频电流
Δiαβ1s=Δiαβ1i+Δiαβ1l
(15)
式中:Δiαβ1s为第一套绕组某一时刻的电流采样值;Δiαβ1l为第一套绕组该时刻电流的基频分量;Δiαβ1i为第一套绕组该时刻电流的高频分量。
2套绕组同时注入高频方波时,可以提取2套绕组的高频电流。提取完高频电流信号之后,从高频电流中分离位置角误差信号。传统的提取方法,只提取一套绕组的位置误差信息,但是误差信息有不确定性,难以避免提取出较大的位置误差信号,从而使估计的位置出现大的偏差和转矩的波动。
为了克服这一问题,本文提出双绕组位置误差最小提取方法,其原理如图4所示。
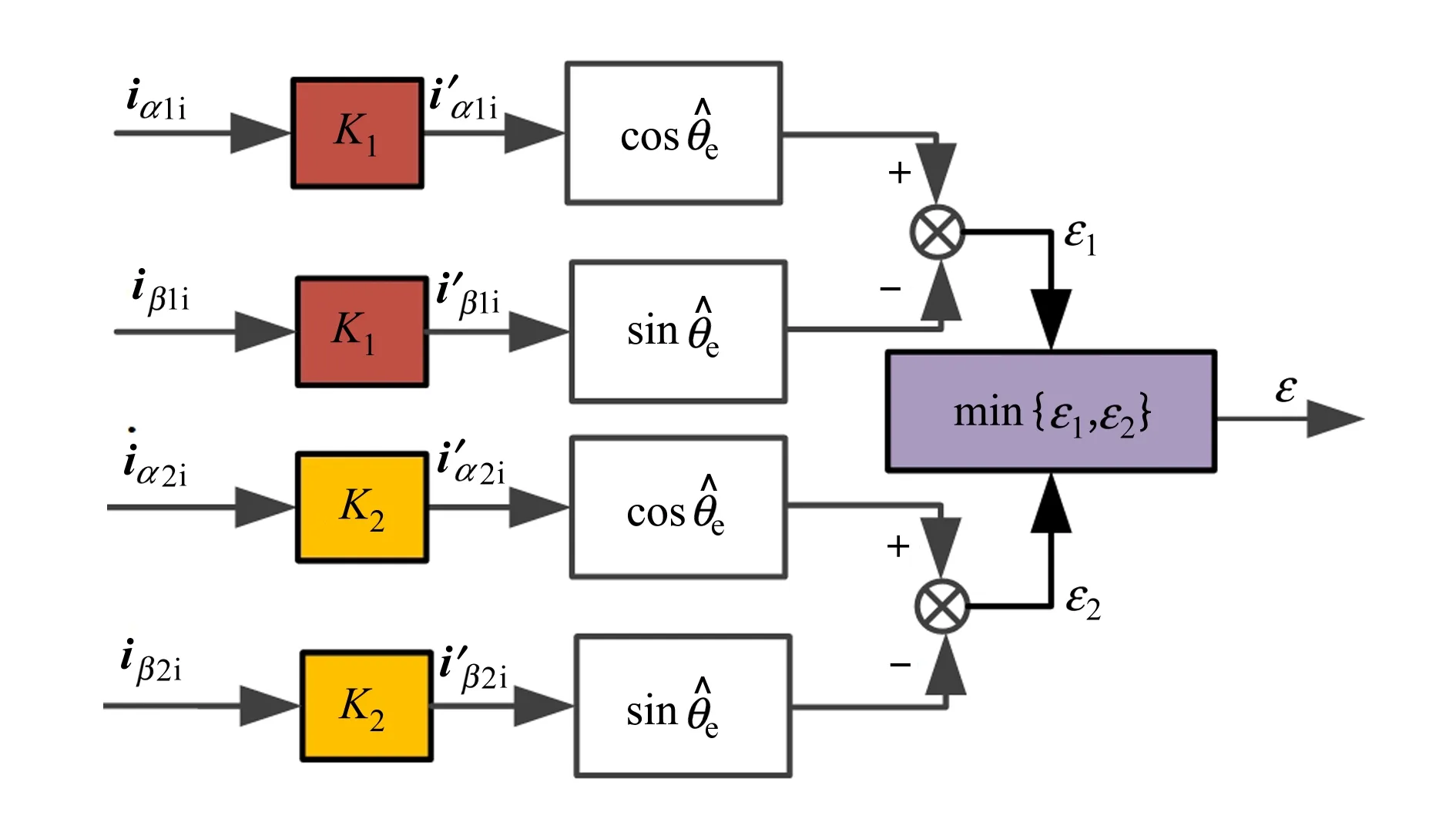
图4 双绕组位置最小误差提取原理框图
提取2套绕组的高频电流信号之后分别提取2套绕组的位置误差信号,再通过比较的方法,得到同一时刻最小的位置误差。通过该方法降低误差波动,提高位置角估计精度,同时尽可能少地增加系统计算量。
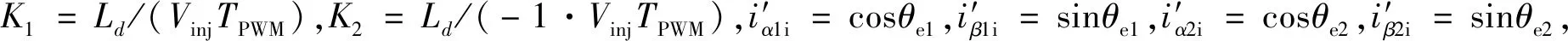
由图4可得
(16)
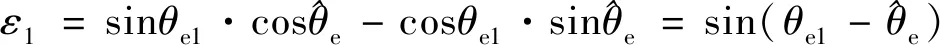
(17)
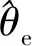
(18)
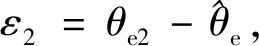
在得到转子位置角最小误差ε后,使用龙贝格观测器跟踪实际的电机转子位置,其原理框图如图5所示。
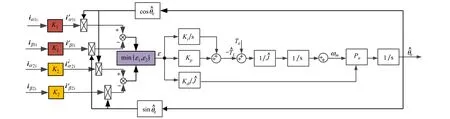
图5 龙贝格观测器原理框图
3 仿真验证
在MATLAB/Simulink中搭建同相位DW-PMSM无位置传感器控制系统仿真模型,以验证本文提出的方法。DW-PMSM本体相关参数如表1所示。
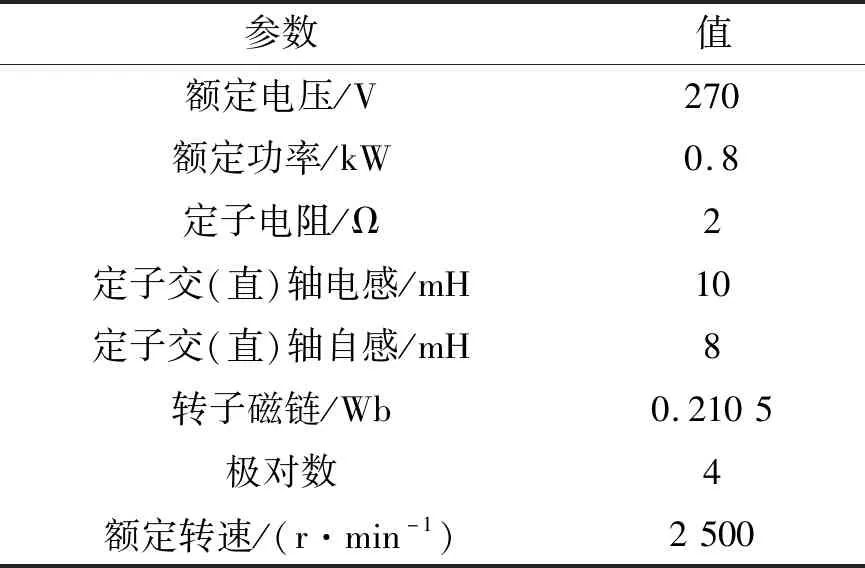
表1 DW-PMSM本体模型参数
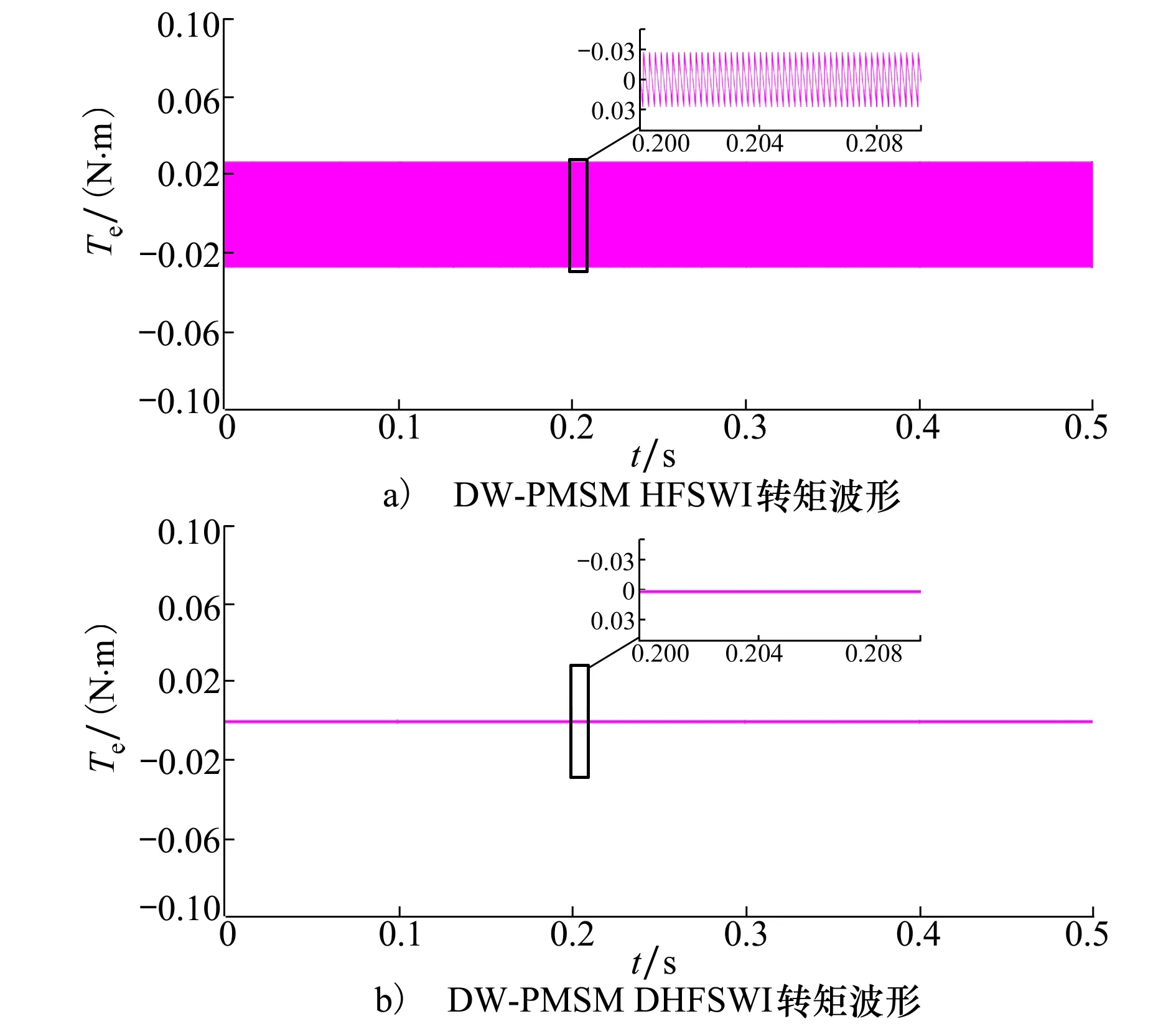
图6 0 r/min DW-PMSM转矩波形
为了验证DHFSWI能够消除高频转矩脉动,给定转速为0 r/min,即只注入高频方波,注入信号的频率为10 kHz,幅值为40 V,系统仿真时间为0.5 s,空载运行。图6为0 r/min DW-PMSM单套绕组注入高频方波时和2套绕组同时注入高频方波时的转矩波形。对比图6a)与图6b)可知,单套绕组注入高频方波时高频转矩的幅值为±0.027 N·m;2套绕组同时注入时高频转矩幅值几乎为0 N·m,高频转矩完全消除。由此可见,本文所提的双高频方波注入法是正确的。
给定转速为60 r/min,负载为1.5 N·m,以验证零低速下双绕组位置误差最小提取方法的有效性。图7为60 r/min DW-PMSM单绕组注入高频方波时和2套绕组同时注入高频方波时的转子位置估计误差,其中图7c)在0.25 s时刻由HFSWI切换为DHFSWI。
对比图7a)与图7b)可知,单套绕组注入高频方波时,位置角估计误差最大值为0.018 rad;2套绕组同时注入高频方波时的转子位置估计误差最大值为0.002 rad,误差减小了88.9%。由图7c)可知,切换后的转子位置估计误差明显减小。这证明了双高频方波脉冲注入时,提取2套绕组的最小位置误差,利用最小误差追踪转子位置,可以提高位置角的估计精度。
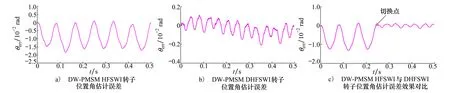
图7 60 r/min DW-PMSM转子位置角估计误差
4 实验验证
为进一步验证本文提出方法的有效性与正确性,进行了DW-PMSM无位置传感器控制系统试验。控制器硬件平台控制核心使用TMS320F28335数字信号处理器,斩波频率为10 kHz,注入信号的幅值与频率与仿真实验保持一致,实验平台如图8所示。DW-PMSM本体参数如表1所示。

图8 实验平台
图9为给定转速0 r/min、负载为0时,DW-PMSM只注入高频信号的空载运行转矩实验结果,高频转矩由公式(8)计算得到。比较图9a)与图9b)可知,单绕组注入时的转矩幅值在±0.03 N·m范围内,双绕组注入时的转矩幅值接近于0 N·m,此结果说明了零低速下DW-PMSM无位置传感器控制,分别给2套绕组注入(1)式和(14)式的高频方波时,有效消除了电机的高频转矩脉动。
图10为转速60 r/min、负载为1.5 N·m,DW-PMSM转子估计位置角误差实验结果,对比图10a)和图10b)可知,单套绕组注入时的转子位置角估计误差最大值为0.01 rad;双绕组注入高频方波时转子位置角估计误差明最大值为0.004 rad,误差降低了60%,系统稳定性显著改善。
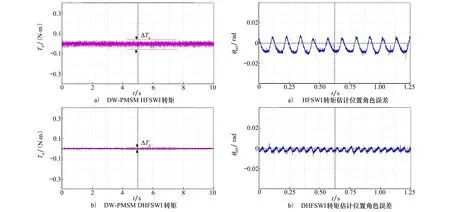
图9 0 r/min DW-PMSM转矩实验结果图10 60 r/min DW-PMSM转子估计位置角误差实验结果
5 结 论
本文研究了基于高频方波注入法的DW-PMSM无位置传感器控制存在的转矩脉动问题,分析了高频转矩脉动产生的原因,提出了一种双高频方波注入法。该方法利用DW-PMSM拥有2套绕组的特殊结构,在2套分别绕组注入高频方波信号,使同一时刻产生的高频转矩脉动相互抵消,故消除了高频转矩脉动。此外,设计出基于双高频脉冲注入的双绕组位置误差最小提取方法,提取2套绕组高频信号中的位置误差信息,比较得到同一时刻最小的位置误差,利用该最小误差追踪实际位置,在尽量减小计算量的同时,提高了转子位置估计精度。

