基于统计模型的西江枯季中长期径流预报研究

蓝羽栖，张 尹，农振昌，韦永江

(1.水利部珠江水利委员会水文局，广东 广州 510611；2.龙滩水电开发有限公司龙滩水力发电厂，广西 河池 547300)

流域水安全保障是维持经济社会高质量发展的重要一环，在新形势新背景下，保障流域水安全对经济社会的发展有着至关重要的作用[1]。然而，随着经济社会的快速发展，受咸潮、水污染和过度开发等问题的威胁，枯水期水资源供需矛盾愈发突出[2]。西江作为珠江流域来水的主要来源，其中长期来水预报对于珠江下游特别是珠江三角洲枯水期意义非凡。2021年汛期，西江来水为1946年以来同期第四枯，主汛期(6—8月)“当汛不汛”，来水均持续偏少。且流域没有出现编号洪水，西江梧州站最高水位为近3年最低，受降雨偏少影响，2021年汛期，西江流域骨干水库来水较多年同期偏少3～4成。面对前期不容乐观的来水形势，此时，可靠的中长期径流预报成为了实现西江枯水期水库群联合优化调度、提高水资源利用效率的关键前提，对抗旱保供水工作具有深刻的科学价值。为提高西江水量调度水平，探求流域内主要站点和重要水库中长期径流预报方法具有重要意义。

针对中长期径流预报，目前通行的方法是在分析水文要素自身的演变规律或挖掘与径流相关的前期水文气象资料的基础上，构建径流时间序列模型或前期水文气象要素与预报月径流的映射关系，从而提供科学的、预见期较长的径流预测结果。近年来，针对统计模型在水文领域中的应用已有了诸多研究，随着计算机的应用与发展，机器学习也逐步被引入到中长期预报中。目前常用的统计学方法有随机森林法[3-4]、神经网络算法[5]、季节自回归等[6]，如胡义明等[7]基于AdaBoost模型、随机森林模型和支持向量机模型在淮河流域进行了月径流预报，比较分析了各模型的预报效果和特点，发现AdaBoost模型整体上优于其他2个机器学习模型；郦于杰等[8]将支持向量回归机应用于汉江皇庄站的中长期径流预报，并对预报结果进行了不确定性分析，实现了高精度的定值预报并以置信区间的方式量化了预报的可靠度；常新雨等[9]采用灰色关联分析法筛选预报因子，构建了基于数据驱动的深度神经网络、Elman神经网络和支持向量机3种模型并运用于黄龙滩水库旬月径流预报，发现支持向量机在洪峰预报上误差更小。上述研究大多采用的是机器学习方法，也均取得了较好的预报效果。然而，尽管机器学习方法学习能力强、容错性能高，但对数据容量具有较高要求，相比之下统计相关分析类和时间序列类方法原理简单、应用方便、耗时短，因此后者仍是实际中长期径流预报应用的常用方法。鉴于此，本文基于均生函数、周期分析、多元逐步回归3种统计模型对西江流域枯季月径流和整个枯水期径流开展应用研究。

1 研究区域及资料

西江是珠江流域的主干流，发源于云南省曲靖市乌蒙山余脉的马雄山东麓，自西向东流经云南、贵州、广西、广东4省(自治区)，至广东佛山市三水区思贤滘，全长2 075 km，平均坡降0.58‰，流域面积353 120 km2，占珠江流域总面积的77.8%。干流从上而下由南盘江、红水河、黔江、浔江及西江5个河段组成。本文以龙滩水库和梧州水文站为代表进行枯季径流中长期预报方法的应用研究。

龙滩水库位于西江流域干流红水河河段(图1)，是广西境内最大的水电工程，也是西江防洪工程体系的控制性工程。龙滩水库以发电为主，兼具防洪、航运等综合效益。坝址以上流域面积98 500 km2，占红水河流域面积的71.2%。本文选取龙滩水库1958—2020年天然径流枯水期6个月(10月、11月、12月、次年1月、次年2月、次年3月)的数据，分别对各月、整个枯水期建立统计模型进行径流模拟，其中1958—2004年采用龙滩实测入库流量，2005—2020年采用经上游天生桥一级水库、光照水电站还原后的龙滩天然入库流量。

梧州水文站位于西江干流与支流桂江汇合口以下约3 km处(图1)，东经111°20′、北纬23°28′，是西江流域的出口控制站，集水面积327 046 km2。本文选取梧州站1963—2020年天然径流枯水期6个月的数据，其中1963—2005年采用梧州实测流量，2006—2020年采用经上游天生桥一级水库、光照水电站、龙滩水库、百色水库4座水库还原后的梧州天然流量。

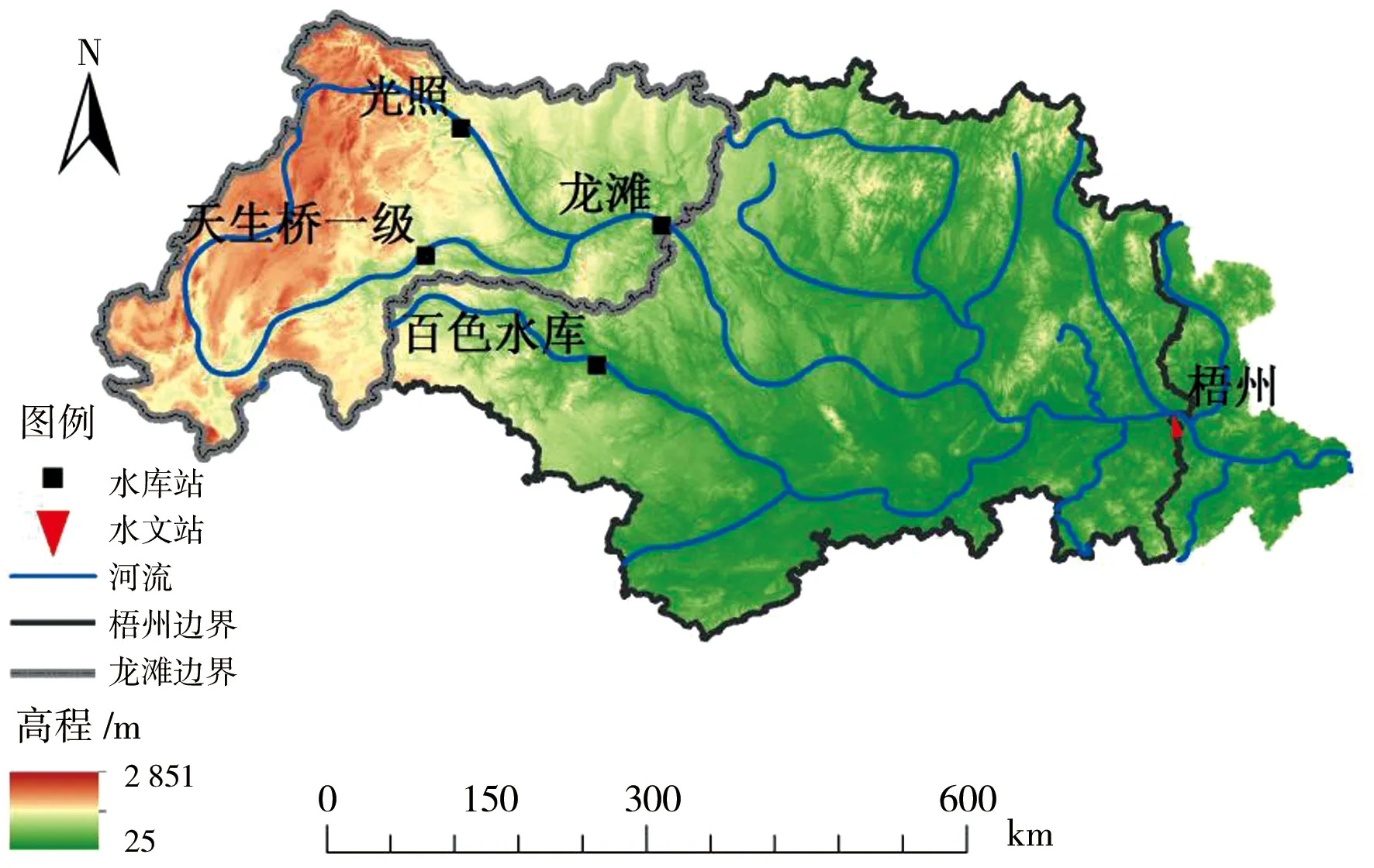
图1 研究区域

收集了国家气候中心1956—2020年的130项气候监测指数资料(由于需要利用前期气候指数资料，故起始年份向前推2年)、龙滩水库和梧州以上流域的前期降雨流量资料(4—9月)作为多元逐步回归的初选因子集。

2 研究方法

2.1 均生函数

均生函数预报方法的基本思想是假定事物过去存在的趋势会延伸到未来，在分析时间序列变量的基础上构建预报模型，通过向外延伸时间趋势进而确定未来预报结果[10-11]。

设任意长度的时间序列X(t) (t=1，2，…，N)，构造其均生函数如下：

(1)

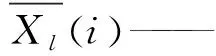
由此得到L(L=lmax=[N/2])阶均生矩阵，通过对均生函数作周期外延进一步构造出外延矩阵，最后从中筛选出B个相关性强的序列，并基于此构建多元回归模型进行模拟预测。

2.2 周期分析

周期分析法的基本思想是将变量随时间的变化当做是由多个不同周期的周期波叠加而成的[12-13]。在给定置信度条件下，采用F检验的方法识别周期波，并对所识别的各周期波进行外延，线性叠加后可用于预测。设水文要素序列x(t)，周期分析法基本计算式如下：

(2)

式中Pi(t)——第i个周期波序列；l——识别到的周期波个数；ε(t)——误差项。

2.3 多元逐步回归

采用气象因子作为预报因子进行多元回归计算的方式较为常见[14-15]。通过对在国家气候中心网站下载的88项大气环流指数、26项海温指数和16项其他气象指数，共计130项天气学因子与对应的水文要素进行分析综合，同时考虑前期流域降雨、江河来水等因素与预报对象具有较大相关性，本文将其与上述130项天气学因子共同作为预报因子，用逐步回归分析方法与预报对象建立方程，并从中筛选出物理意义明确、统计贡献显著的预报因子，对预测对象进行定量预测。多元逐步回归基本计算式如下：

y=b0+b1·x1+b2·x2+b3·x3+…+bn·xn

(3)

式中y——预报对象；bn——回归系数；xn——预报因子；n——因子个数。

2.4 精度评价指标

2.4.1变幅误差(M)

采用GB/T 22482—2008《水文情报预报规范》[16]中针对中长期定量预报的精度评定方法，即以多年同期实测变幅的20%作为许可误差，当预报值与实测值间的绝对误差小于许可误差时判定为合格(M<20%)，否则不合格。M计算方法如下：

(4)

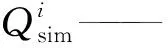
2.4.2平均绝对百分比误差(MAPE)

该指标反映了预报值相对于实测值的偏离程度，MAPE越接近于0，则模拟效果越好。MAPE计算方法如下：

(5)

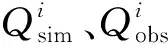
3 预报结果分析

以龙滩水库和梧州水文站为例，采用上述均生函数、周期分析和多元逐步回归3种统计方法分别构建径流预报模型，预报时段为当年10月至次年3月各月(6个时段)和整个枯水期(1个时段)，即2个断面各有3×7个预报模型。考虑到率定期与验证期的长度比一般符合3∶1左右的原则，对于龙滩水库，以1958—2004年作为模型率定期，2005—2020年作为模型验证期；对于梧州站，以1963—2005年作为率定期，2006—2020年作为验证期。采用变幅误差和平均绝对百分比误差2个指标对各模型预报结果进行精度评定，龙滩水库、梧州站各月和整个枯水期的径流预报精度情况见表1、2。

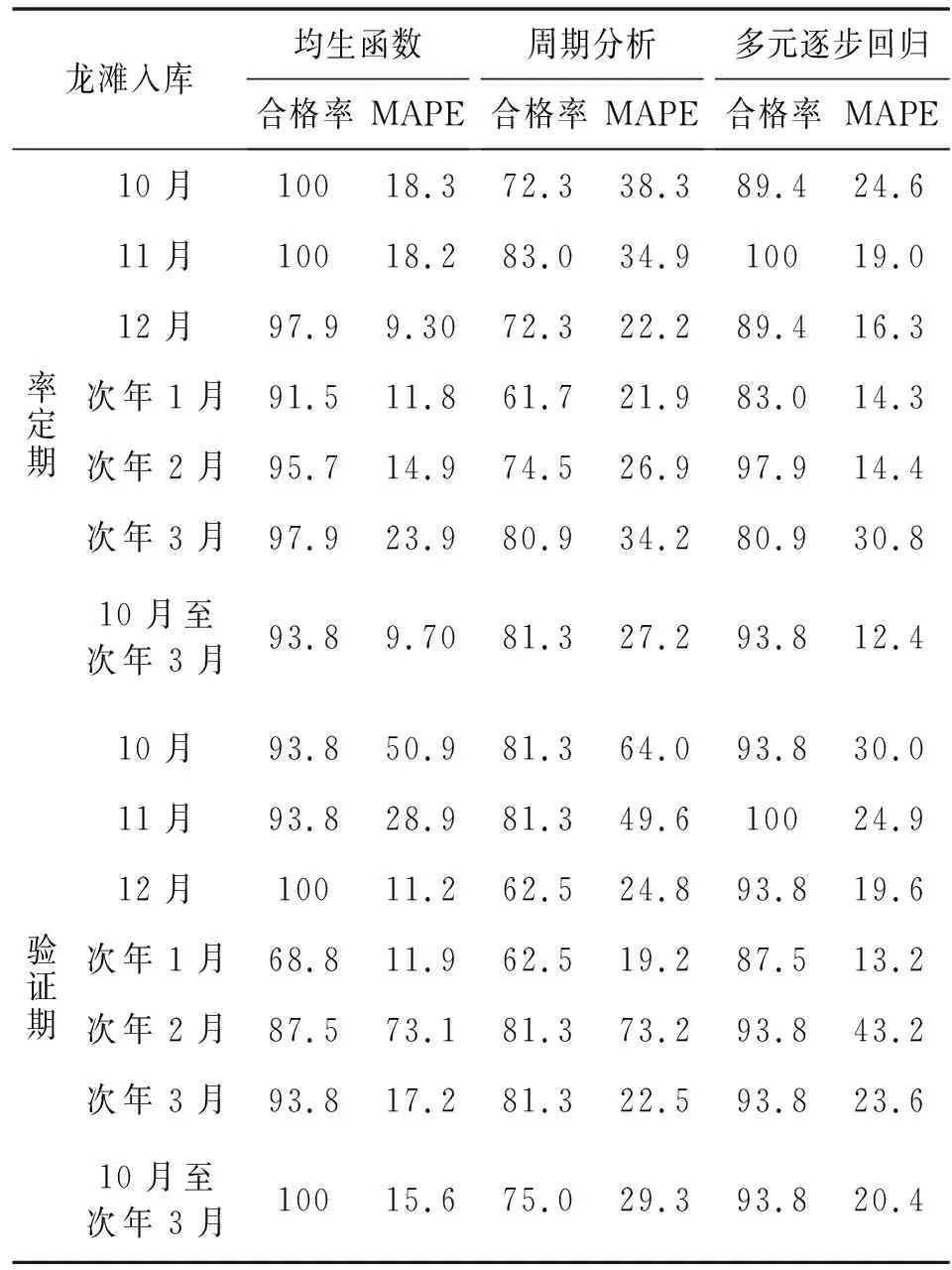
表1 龙滩入库各月、枯水期径流预报精度统计 %

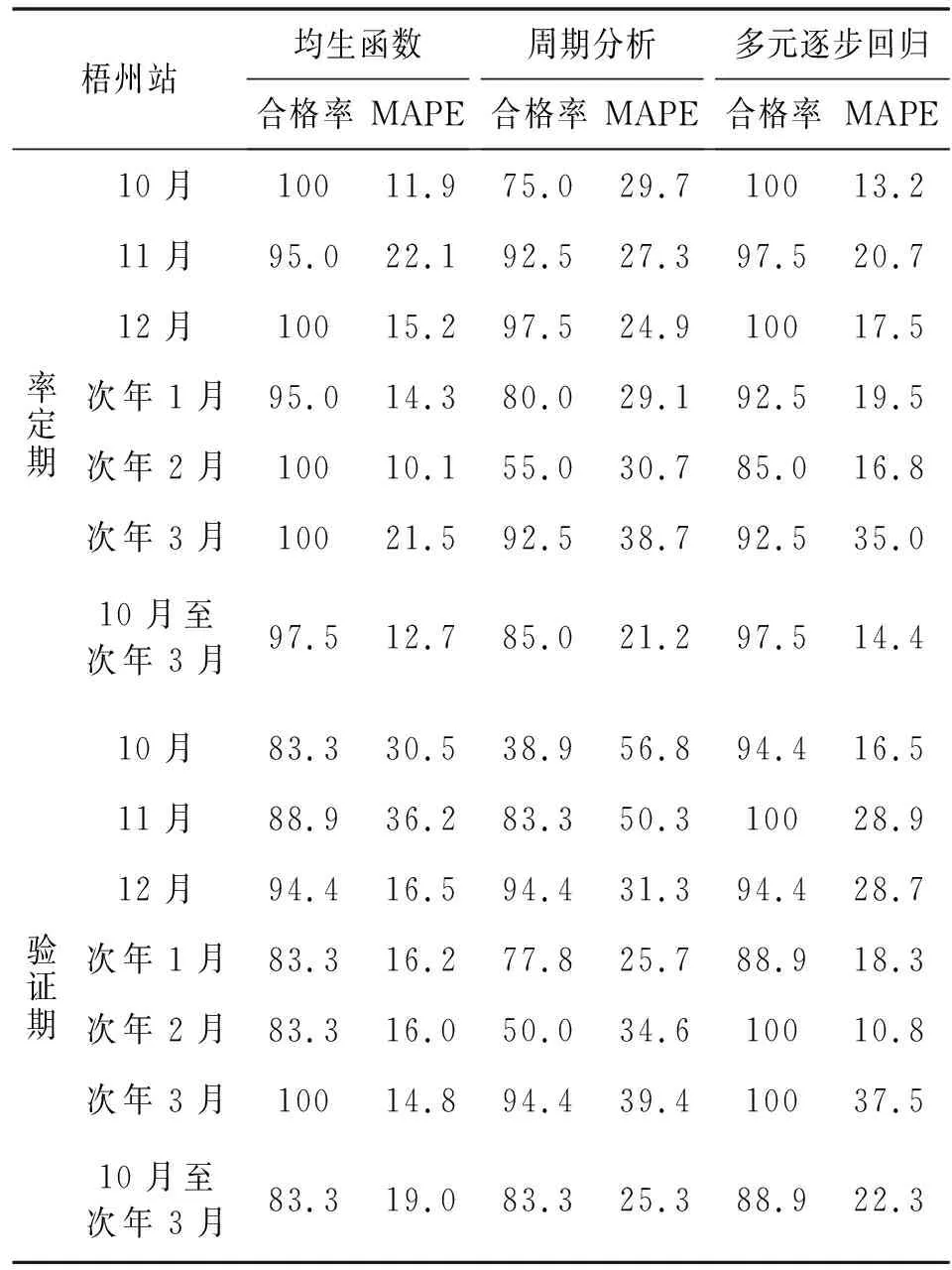
表2 梧州站各月、枯水期径流预报精度统计 %

将2个断面统一考虑，由表1、2可知，在率定期内，3种模型10月至次年3月各月和整个枯水期(10月至次年3月)的平均合格率均超过了75%，其中均生函数模型合格率在91.5%～100%，平均合格率为97.4%，多元逐步回归模型在80.9%～100%，平均合格率为92.8%，周期分析较其他2个模型略低，2个断面14个模型的合格率在55.0%～97.5%，平均合格率为78.8%；3种模型对应平均MAPE值均在30%以内，其中均生函数、多元逐步回归2个模型平均MAPE值分别为15.3%和19.2%，均在20%以内，而周期分析模型相对较高，平均MAPE值为29.1%。综合来看，3个模型在率定期均具有良好的预报效果，其中均生函数模型和多元逐步回归模型明显优于周期分析模型。

相对于率定期而言，验证期的预报精度略有降低，其中均生函数模型验证期平均合格率为89.6%，周期分析模型为74.8%，分别较率定期下降了7.8%和4.0%，而多元逐步回归模型不降反升，平均合格率为94.5%，较率定期上升了1.7%；3种模型对应平均MAPE值较率定期总体存在不同程度的增涨，相似地，其中均生函数模型和周期分析模型均增涨10%，而多元回归模型仅增涨5%，说明多元回归模型具有较强的泛化能力，模型稳定性更强，这可能是因为相比前两种模型仅分析自身演变规律，多元回归模型使用前期水文气象因子作为依据，获得了更多的预报信息。精确到各月时发现，龙滩水库次年二月的MAPE值均较高，但合格率却不低，这是因为2010年2月龙滩天然来水是1958年以来最枯，较多年同期偏少92%，所以该年MAPE值异常偏高，导致平均MAPE值也更高。

为了更直观地查看和对比3种模型的预报效果，图2、3分别给出了整个时间序列内上游龙滩水库和下游梧州站预报值和实测值的散点关系。

a)均生函数预报

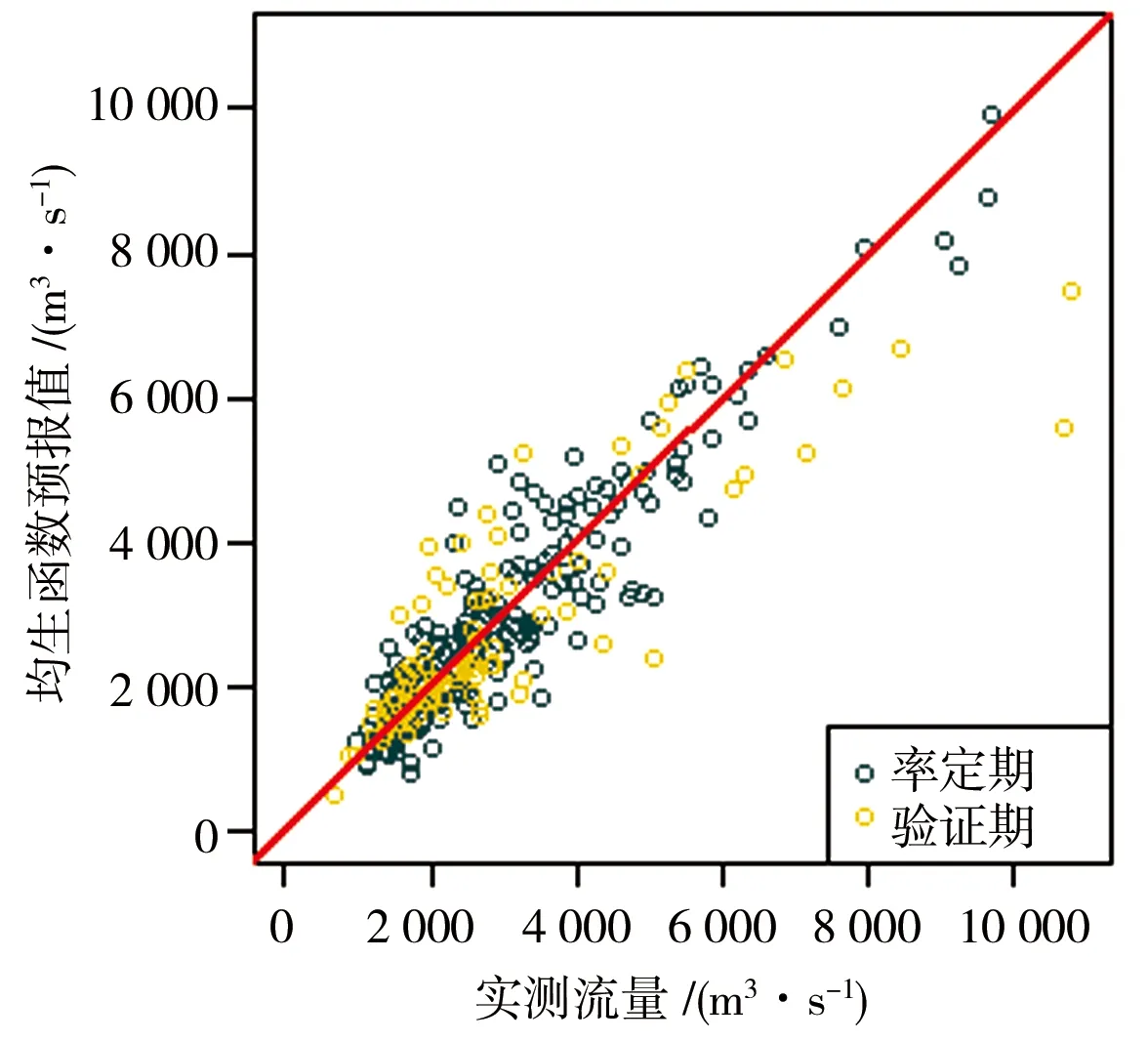
a)均生函数预报

由图2、3可以明显看到，在率定期与验证期内，均生函数模型和多元逐步回归模型的散点均聚拢分布在45°线(图中红线)附近，且线两侧散点个数比重相当，说明2个模型对枯水期各月流量均具有较好的预报效果。相比之下周期分析模型45°线两侧虽也分布均匀，但散点较离散，且随着量级增加，预报的偏差越大，上半部分散点大多分布于红线以下，即在流量量级较大时周期分析模型存在预报偏低现象。由此可知，均生函数模型和多元回归模型的预报精度整体较周期分析模型更高，在高流量值的预报上误差更小。另外，通过对比龙滩入库和梧州站可以看到，前者各模型散点分布更聚集，究其原因，可能与梧州站以上众多水库的调度调节有关，随着水库的增建和人类活动的影响增加，经4座水库还原后的梧州站还原流量并不是真正的天然流量，序列资料一致性遭到一定程度的破坏，导致模型精度降低。

4 结论

可靠的中长期径流预报是流域开展科学的枯水期水量调度工作的重要依据。基于均生函数、周期分析、多元逐步回归3种统计模型，本文对西江上游龙滩水库、下游梧州水文站进行了自10月至次年3月各月以及整个枯水期的径流预报，得出的结论如下。

a)3种模型均呈现出较好的预报效果，率定期和验证期平均合格率均在75%以上，MAPE值基本在30%以内，其预报结果可为西江流域水量调度方案的编制提供技术参考。其中均生函数和多元逐步回归的预报精度相近，且明显高于周期分析，特别是在对极值的预报能力方面。

b)与均生函数和周期分析相比，多元逐步回归模型稳定性更强。前两者验证期平均合格率较率定期均有所下降，后者不降反升，且仍保持在90%以上，MAPE值的增涨也最缓慢。

c)在预报天然流量时，序列资料的一致性程度会影响预报精度。就模型预报与实测的整体拟合情况而言，上游龙滩水库较下游梧州站拟合得更好，这可能与梧州水文站作为西江控制站受到众多水库共同调控的影响有关。

d)由于计算思路不同，统计模型各有优劣，目前还不存在一个具有绝对优势的通用模型，因此可以考虑通过融合多种模型的方式，达到优化预报效果的目的。