基于流固耦合方法的大口径蝶阀的防振优化设计

张伟政，庞益祥，赵鹏博，张俊涛

（兰州理工大学 石油化工学院，兰州 730050）

0 引言

阀门作为管路流体输送系统中的重要控制部件，在化工、机械、石油、航空航天等领域有着广泛的应用，三偏心蝶阀以其密封性能好、适用范围广、寿命长等特点被广泛应用［1-4］。特别是在大口径方面、三偏心蝶阀能够达到零泄漏，与其他阀门相比优势明显。许多国内外学者针对大口径、高温、高压三偏心金属硬密封蝶阀展开了广泛研究，但是针对大口径三偏心金属硬密封蝶阀的蝶板和阀杆的应力变形及共振特性分析的研究较少。韩志杰等［5］运用CFD对三偏心蝶阀的流场进行模拟研究及优化，降低了流阻系数，进一步提高了阀门流通性能。LISOWAKI等［6］运用CFD方法对控制阀的流场进行模拟分析。何庆中等［7-8］运用CFX数值模拟方法对大口径蝶阀内部流场特性进行模拟，并进行结构优化。李树勋等［9］利用热流固耦合的方法对蝶阀进行了共振预测研究。张伟政等［10］针对蝶阀流固耦合特性及共振特性进行了研究，得出了阀门位于30%开度和50%开度时，蝶板和阀杆容易发生共振的结论。沈春颖等［11］进行了平面直升闸门流固耦合振动同步测试模型试验研究。李树勋等［12］利用数值模拟方法，针对蒸汽疏水阀节流振动的问题进行研究，找到了流激共振发生的原因。刘丽等［13］对某大型化工厂管道的振动问题进行了分析，并提出了减振措施。SHIPMAN等［14-15］采用数值模拟方法，对稳压阀和氢气进气阀的压力进行频域分析，从而发现阀门异常振动的原因。孔祥帅等［16］利用数值模拟分析与实验测试相结合的方法找到了防止三偏心蝶阀蝶板与卡门涡街的脱落发生共振的方法。这些研究都是针对口径较小的阀，且只研究了阀门产生共振的原因，并没有针对蝶板和阀杆在不同开度下的共振特性进行结构优化设计。

本文采用有限元法对三偏心金属硬密封蝶阀结构参数进行优化设计，通过数值模拟方法对蝶板和阀杆的应力、变形及共振情况进行分析，并与结构优化前蝶板和阀杆的应力、变形情况进行对比，从而证明优化设计的可行性。

1 结构改进及参数确定

针对大口径三偏心金属硬密封蝶阀在30%和50%开度容易发生共振，在75%开度应力和变形过大的问题进行分析，得出可能是由于蝶板背部的弯曲度太大，导致边缘厚度相较中间位置厚度薄，自身的强度不够所引起的。提出通过改变蝶板背部的弯曲角度的方法，把蝶板背部弯曲角度由15°改为10°，使蝶板背部曲线弯曲的更为平缓，以此来改变蝶板边缘位置的厚度，增加自身的强度，从而实现降低蝶板所受到的应力和变形，同时使结构的振动模态也发生相应的改变，达到在30%和50%开度下避免发生共振的目的。

1.1 几何模型

DN1500蝶阀的蝶板背部角度改变前后对比如图1所示，在阀前阀后增加管道，阀前5DN，阀后10DN，三偏心金属硬密封蝶阀三维模型如图2所示。

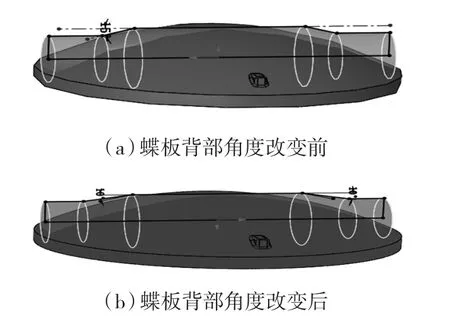
图1 蝶板背部角度改变前后对比Fig.1 Comparison before and after the change of the back Angle of the butterfly plate

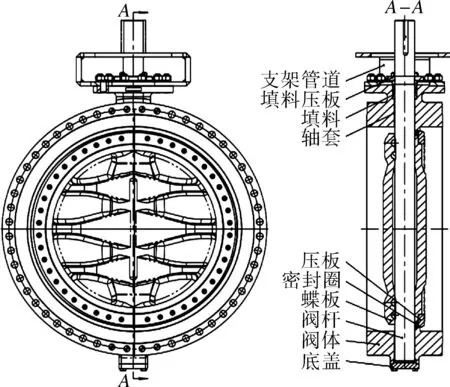
图2 三偏心金属硬密封蝶阀三维模型Fig.2 Triple eccentric metal hard seal butterfly valve

1.2 参数及边界条件的确定

三偏心金属硬密封蝶阀参数见表1。

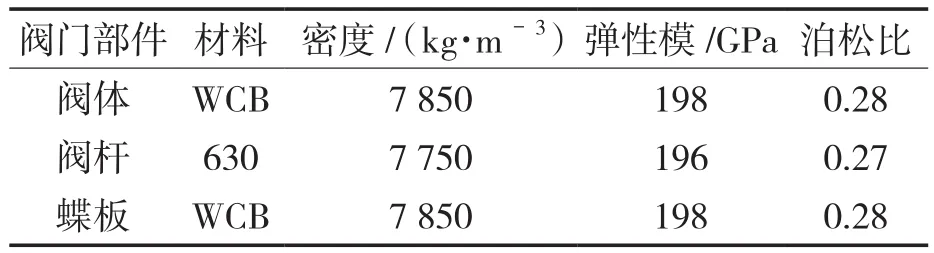
表1 三偏心金属硬密封蝶阀基本参数Tab.1 Basic parameters of triple eccentric metal hard seal butterfly valve

模拟稳态流场时选择无滑移边界条件定义流道及阀内件壁面，残差曲线精度为10-4。根据三偏心蝶阀正常使用时工况，设定进口压力2 MPa，出口压力1.6 MPa，压降为0.4 MPa，介质为液态水。瞬态流场模拟时，设置时间步长为0.000 5 s，计算总时长为1 s。

1.3 网格划分

运用ANSYS Workbench抽取流道后，导入ANSYS ICEM中进行网格划分，采用混合网格的方法来划分网格，中间阀门部分采用四面体非结构化网格，两端管道部分采用六面体结构化网格。网格划分情况如图3所示。

图3 三偏心金属硬密封蝶阀内流道网格划分Fig.3 Internal flow channel meshing of triple eccentric metal hard seal butterfly valve

对划分好的大口径三偏心金属硬密封蝶阀流道网格模型进行网格无关性验证，以50% 开度为例，网格无关性验证见表2。

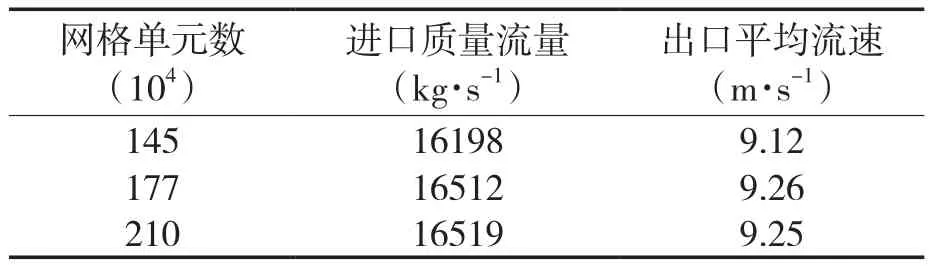
表2 网格无关性验证Tab.2 Grid independence verification

由表2可知，当网格质量为177万时，随着网格数的增大，进口质量流量几乎没有变化，说明再增加网格对计算结果已基本没有影响，所以采用177万的网格数来计算。

2 数值模拟理论

2.1 控制方程

本文所用到的流体力学控制方程有质量守恒方程、能量守恒方程和动量守恒方程。

式中 p ——微元体上的静压力，Pa；

τij——微元体上的应力张量；

gi—— i方向的重力，N；

Fi—— i方向的外部体积力，N/m3。

2.2 湍流模型

为了保证计算的稳定、快速收敛，湍流模型选用标准k-ε模型。根据质量守恒和动量守恒，不可压缩流体的湍流动能k及湍流动能耗散率ε的输运方程［17-20］为：

式中 μ ——涡黏性系数；

pk——湍流动能生成项。

k-ε模型中经验常数分别取值为：C1=1.44，C2=1.92，Cμ=0.99，σk=0.0，ε=1.3。

3 数值模拟分析结果

3.1 优化前后流场特性对比分析

对改进后的三偏心金属硬密封蝶阀，选取30%、50%和75%开度来进行流场模拟分析，边界条件不变，通过对比优化前后其内部流场特性来研究优化效果。

3.1.1 优化前后压力场结果对比分析

优化前后蝶阀在30%、50%和75%开度下的压力分布对比如图4所示。由图4可知，当阀门处于30%开度时，优化后的阀门比优化前的阀门蝶板上端部分压力梯度变化更加明显；当阀门处于50%开度时，优化后阀门比优化前的阀门阀后压力梯度变化小；当阀门处于75%开度时，优化后的阀门在蝶板的上端一侧位置未出现明显的压 差，大大减小了此处所受到压力波动的影响。

图4 优化前、后不同开度下对称面上压力分布对比云图Fig.4 Comparison of pressure distribution on symmetrical surface with different opening before and after optimization

3.1.2 优化前后速度场结果对比分析

优化前后蝶阀在30%，50%和75%开度下速度分布对比如图5所示。

图5 优化前、后不同开度下对称面上速度分布对比云图Fig.5 Comparison of velocity distribution on symmetry surface with different opening before and after optimization

由图5可知，当阀门处于30%开度时，优化后的阀门较优化前的阀门阀后速度梯度更平滑且在蝶板上端处最大流速区域较少，流速较低；当阀门处于50%开度时，优化后的阀门比优化前的阀门阀后最大流速区域相对较少，但是其最大流速相比优化前最大流速较高；当阀门处于75%开度时，优化后的阀门比优化前的阀门阀后流动能更快的趋于稳定，并且其最大流速相比优化前的最大流速较高。

3.2 优化前后流固耦合特性对比分析

针对三偏心金属硬密封蝶阀在75%开度时会出现应力和变形过大的问题，因此对改进后的三偏心金属硬密封蝶阀也选取75%开度进行其流固耦合特性分析，通过对比优化前后三偏心金属硬密封蝶阀阀内的应力和变形来研究其优化效果。

3.2.1 优化前后变形结果对比分析

对比分析优化前后阀门在不同开度时的变形情况，以75%开度为例，优化前后变形对比如图6所示。同时为了能够清晰地了解阀门在优化后蝶板和阀杆在不同开度下的变形情况，绘制了优化前后不同开度下轴向最大变形对比曲线如图7所示。

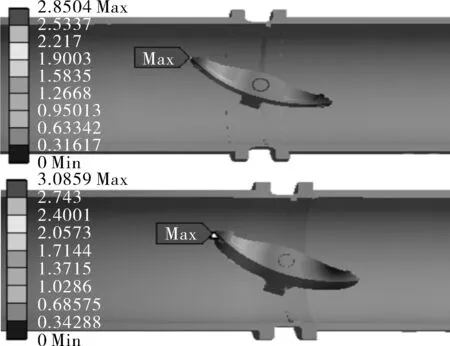
图6 优化前、后75%开度下蝶板和阀杆的变形对比云图Fig.6 Deformation comparison cloud diagram of disc and stem with 75% opening before and after optimization

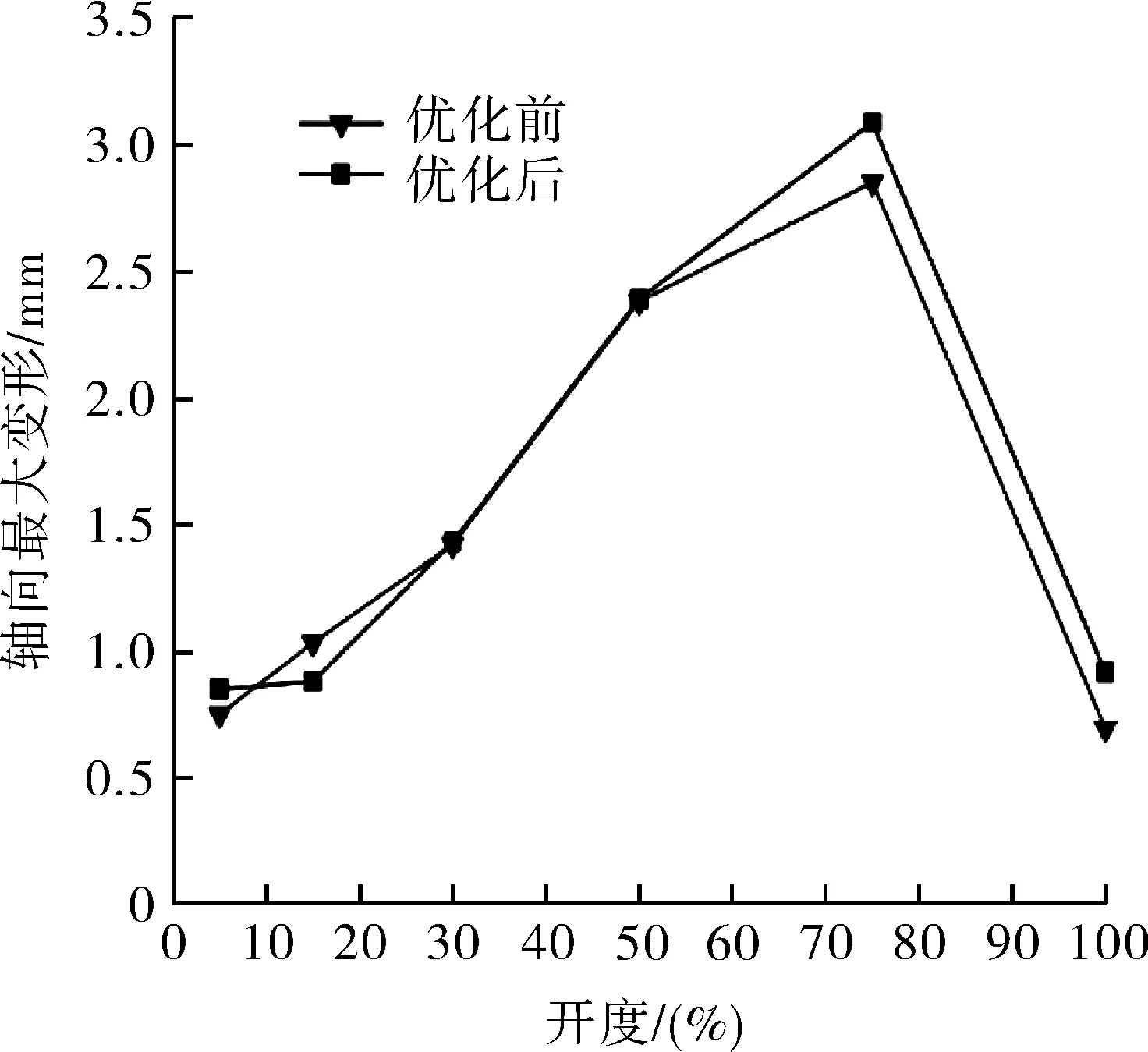
图7 优化前、后不同开度下轴向最大变形对比曲线Fig.7 Comparison curves of maximum axial deformation with different opening before and after optimization

由图6可知，优化前、后蝶板和阀杆的轴向最大变形的区域是一样的，但优化后的蝶板和阀杆的轴向最大变形还大了0.235 5 mm，造成这样的原因可能是优化后蝶板周围的流动状态发生相应的改变而引起的，通过75%开度下优化前后的速度对比云图可知，优化后的蝶板前端流速是大于优化前的，因此优化后蝶板前端所受到的压强较大，相应此时轴向最大变形与优化前相比也较大。

由图7可知，随着阀门开度的逐渐增大，优化后蝶板和阀杆的轴向最大变形在5%，75%和100%开度时是大于优化前蝶板和阀杆的轴向最大变形；在15%开度时蝶板和阀杆的轴向最大变形是小于优化前蝶板和阀杆的轴向最大变形。从整体上能够明显看出来，优化前和优化后的整体趋势是一样的，都是随着阀门开度的逐渐增大，蝶板和阀杆的轴向最大变形逐渐增大，并在75%开度时达到最大，然后开始逐渐减小。

3.2.2 优化前后等效应力结果对比分析

对比分析优化前后阀门在不同开度时的等效应力情况，以75%开度为例，优化前后等效应力对比云图如图8所示。为了能够清晰观察，绘制了优化前、后不同开度下最大等效应力对比曲线图，如图9所示。

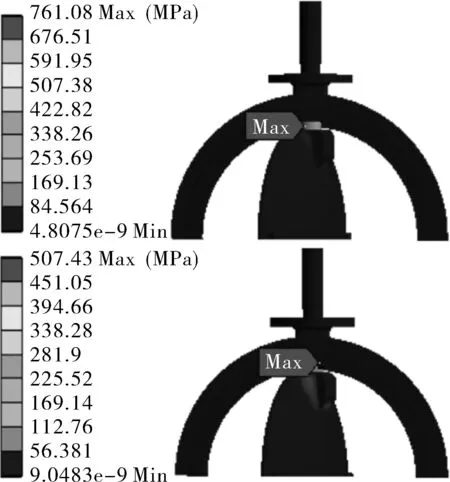
图8 优化前、后75%开度蝶板和阀杆的等效应力对比云图Fig.8 Comparable cloud diagram of equivalent stress of disc and stem at 75% opening before and after optimization

由图8可知，优化前、后最大等效应力都是位于蝶板上端阀杆处，但优化后的最大等效应力与优化前相比降低了253.65 MPa，优化效果明显。说明改变蝶板背部弯曲角度对于最大等效应力的优化是可行的。

由图9可知，在5%开度时优化后蝶板和阀杆的最大等效应力大于优化前的最大等效应力，在其他开度下均小于优化前蝶板和阀杆的最大等效应力。从整体上看，优化前后的趋势都是先逐渐增大，在75%开度下等效应力达到最大。通过对比可以看出，优化前、后蝶板和阀杆的最大等效应力幅度变化较大，优化效果比较明显。

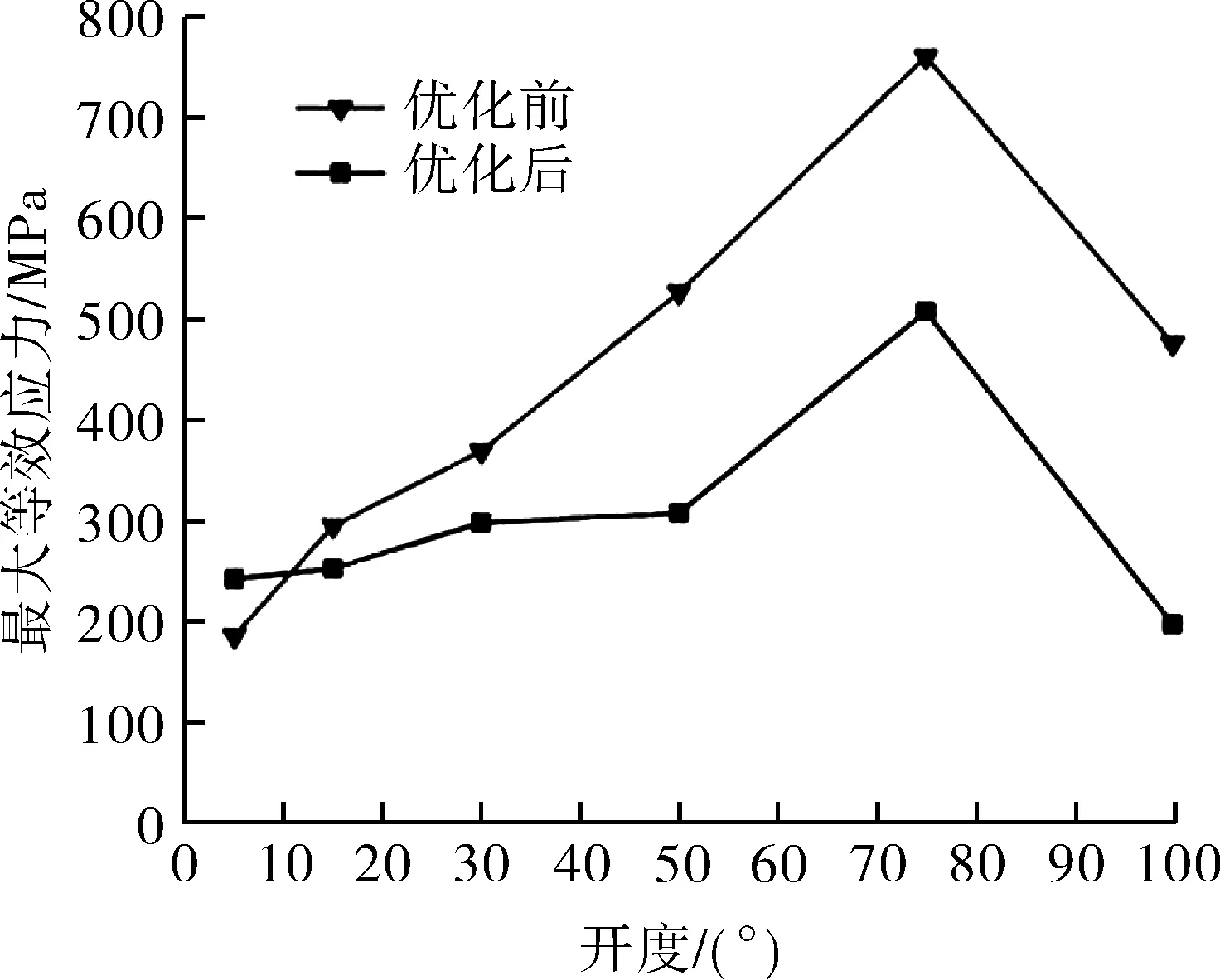
图9 优化前、后不同开度下最大等效应力对比曲线Fig.9 Comparison curve of maximum equivalent stress at different opening before and after optimization

3.3 优化前后共振特性对比分析

优化前蝶阀会在30%和50%开度下发生共振，因此对于优化后同样选取30%和50%开度来进行模态分析、谐响应分析，研究优化后的振动状况。

3.3.1 优化前后模态频率结果对比分析

对比分析优化前后阀门在不同开度下蝶板和阀杆的模态频率和模态阵型图，着重分析了阀门在30%和50%开度时的模态频率和前两阶模态阵型图，其优化前后前两阶模态阵型对比如图10所示。

图10 优化前、后30%和50%开度前两阶模态阵型对比Fig.10 Comparison of the first two modes with 30% and 50% opening before and after optimization

由图10可知，30%开度时和50%开度时优化前、后的前两阶模态阵型图最大变形量和最小变形量区域基本一致，且优化后阀门前两阶振型最大变形量和最小变形量均小于优化前阀门前两阶振型最大和最小变形量，但相差不大。

为了能够更直观分析其模态频率的变化规律，绘制优化前后不同开度下前六阶模态频率对比曲线，如图11所示。

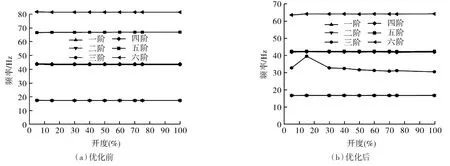
图11 优化前、后不同开度下前六阶模态频率对比Fig.11 Comparison of the first six modes with different opening before and after optimization

由图11可知，同一开度下，优化前后阀门的前六阶模态频率都随着阶数的增大而增大；不同开度下，优化前的阀门各阶模态频率是随着阀门开度的增大几乎不变，而优化后随着阀门开度的逐渐增大，其三阶模态频率先增大逐渐减小并趋于稳定，并在15%开度时达到最大，而其他阶模态频率几乎不变。优化后的阀门前六阶模态频率整体上小于优化前的阀门前六阶模态频率。

3.3.2 优化前后共振结果对比分析

对比优化前后阀门在不同开度下脱落涡频率，并把不同开度下的脱落涡频率与模态频率数据绘制成曲线，如图12所示。

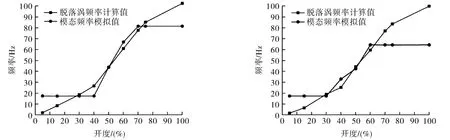
图12 优化前、后不同开度下蝶板和阀杆的脱落涡频率计算值与模态频率模拟值对比曲线Fig.12 Comparison of calculated values of shedding vortex frequency and simulated values of modal frequency of valve plate and stem with different opening before and after optimization

由图12可知，优化前在30%开度和50%开度时，蝶板和阀杆容易发生共振，而优化后，虽然有所改善，但是两者频率仍然很接近，因此可能还会发生共振，但通过对比发现，其振动幅值减小。

3.3.3 优化前后谐响应结果对比分析

利用ANSYS软件模态叠加法对优化后的阀门在30%和50%开度下进行谐响应分析，通过对比优化前后的谐响应分析图来分析具体的共振状况和优化效果，其优化前后在30%和50%开度下蝶板和阀杆的位移响应-频率曲线对比如图13所示。

由图13可知，当阀门处于30%开度时，优化前后的阀门在18 Hz左右出现波峰，其分别对应优化前后一、二阶固有频率分布，此时响应幅值最大，结构会发生共振，但优化前的振幅最大为0.16 mm，而优化后的振幅最大为0.02 mm，优化效果明显；当阀门处于50%开度时，优化前后的阀门在43 Hz左右出现波峰，其分别对应三、四阶和四、五阶固有频率分布，此时响应幅值最大，结构会发生共振，优化前的振幅最大为0.2 mm，而优化后的振幅最大为0.04 mm，优化效果明显。

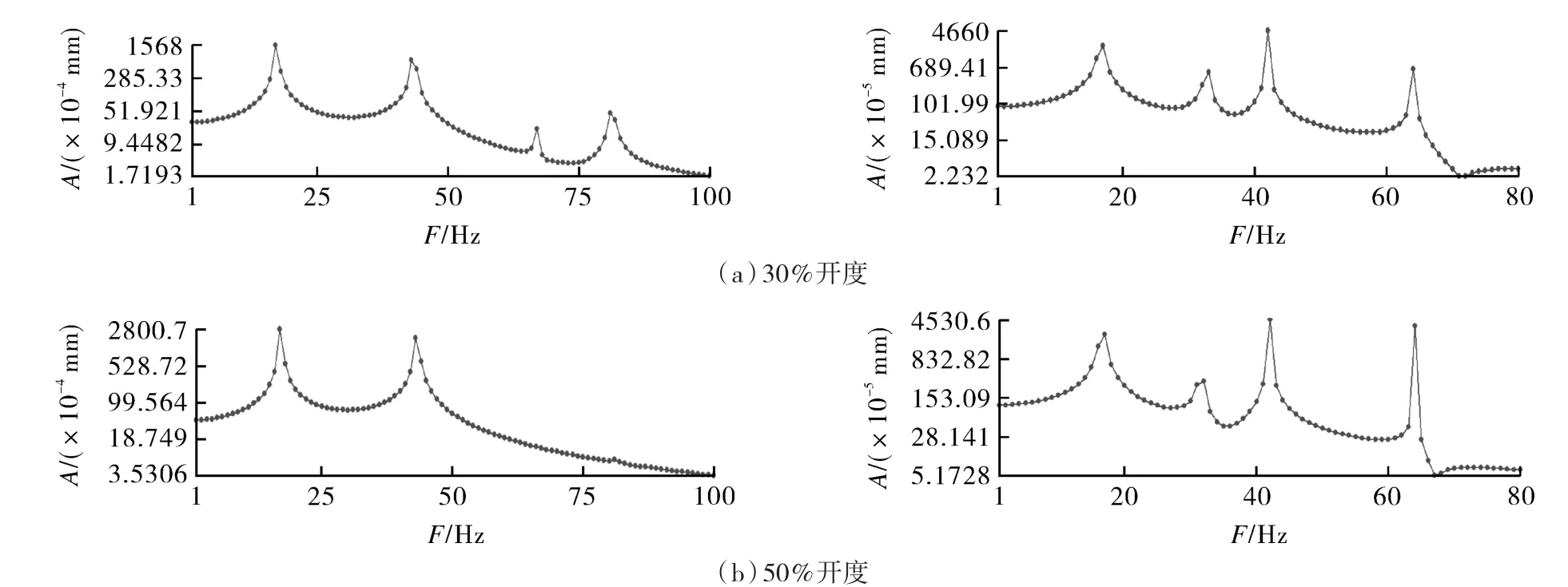
图13 优化前、后30%和50%开度位移响应-频率曲线对比Fig.13 Comparison of 30% and 50% opening displacement response-frequency curves before and after optimization

4 结论

（1）改变蝶板背部的弯曲角度可以使阀内流体的流动状态更快趋于稳定。

（2）优化后蝶板和阀杆应力与之前相比明显减小，优化后的最大等效应力与优化前相比降低了253.65MPa，优化效果明显，证明了优化方法的可行性。

（3）30%开度时，优化前振幅最大为0.16 mm，而优化后的振幅最大为0.02 mm；50%开度时，优化前的振幅最大为0.2 mm，而优化后的振幅最大为0.04 mm。共振幅值明显减小，大大降低了发生共振时对于结构的危害性。