基于点-单元接触模式的水平岩层运动连续-非连续方法模拟

王学滨，薛承宇，岑子豪

(1.辽宁工程技术大学 计算力学研究所，辽宁 阜新 123000； 2.辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000)

采场上覆岩层的开裂和破断在力学上可归结为连续介质向非连续介质转化或非连续介质进一步演化。从力学角度研究此规模较大问题(例如，几公里范围的采场)的难度较大，其中涉及连续介质力学、接触力学、非线性断裂力学和计算力学等分支。正确模拟采场上覆岩层运动过程对于岩层稳定性控制和有关灾害预防具有极其重要的意义。目前，尚缺乏有效的求解手段。

显然，欲模拟连续介质向非连续介质转化或非连续介质进一步演化，有限元方法和有限差分方法等为代表的连续方法无能为力。在以离散元方法和非连续变形分析方法等为代表的非连续方法中，即使在弹性阶段，通常都需要接触面刚度系数等参数；岩层被预先根据经验划分为不同尺寸的块体，这与实际情况有一定差距。兼具连续方法和非连续方法优势的连续-非连续方法被认为在模拟连续介质向非连续介质转化和非连续介质进一步演化方面具有突出的能力，正在快速发展。目前，已应运而生了许多著名的程序或软件，例如有限元与离散元耦合方法[1-2]和拉格朗日元与离散元耦合方法[3]。目前，采用拉格朗日元与离散元耦合方法已经开展了一系列研究[4-9]，效果良好。

本研究介绍了自主开发的拉格朗日元与离散元耦合方法的基本原理，以及以此为基础最新发展的水平岩层运动计算方法，并通过3个采场算例，展现了该方法的优势。

1 拉格朗日元与离散元耦合方法的基本原理

拉格朗日元与离散元耦合方法本质上是连续方法中拉格朗日元方法与非连续方法中离散元方法的耦合方法。拉格朗日元方法被用于求解弹性体的应力和应变问题，离散元方法被用于求解接触和摩擦问题。同时，还需引入强度理论和虚拟裂纹模型以处理开裂和软化问题(软化程度由断裂能控制)。

该方法的适用性包括两方面：其一，连续介质向非连续介质转化研究，例如，完整的连续介质由于应力超标向破裂、分离的非连续介质转化模拟；其二，非连续介质的进一步演化研究，例如，若干叠合在一起的岩层(通过嵌入发生相互作用)运动模拟。本研究的算例即是如此。

该方法由4个模块组成，分别是应力-应变模块、开裂模块、接触-摩擦模块和运动模块。该方法流程图如图1所示。应当指出，在1个时步内，上述4个模块依次被执行1遍，循环的次数被称为时步数目N。当N达到预设的结束时步数目时，循环结束，输出单元和节点等信息。

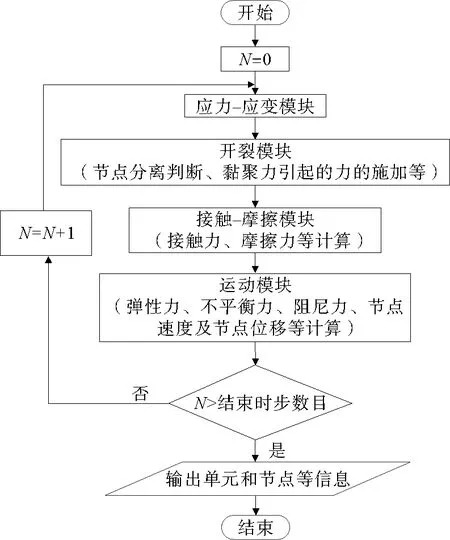
图1 拉格朗日元与离散元耦合方法的流程图

应力-应变模块被用于计算单元的应力和应变，其具体原理同FLAC(连续介质快速拉格朗日分析)。在弹性阶段，对于连续介质，只引入两个弹性参数，无需引入影响应力、应变的有关刚度参数，因而，介质是真正的连续介质。

根据增量形式的线弹性本构方程，由子单元的应变增量Δeij(当i=j时，表示为Δekk)求解子单元的应力增量Δσij：

(1)

式中：K为体积模量，Pa；G为剪切模量，Pa；δij为Kronecker符号，即

(2)

开裂模块被用于处理介质的拉裂和剪裂。利用最大主应力准则判断介质是否发生拉裂，利用莫尔-库仑准则判断介质是否发生剪裂。同时引入I型和II型断裂能。在必要时，单元可以沿对角线开裂。

介质发生拉裂的条件为：

ft=σt-σ3<0，

(3)

式中：ft是拉裂屈服函数；σt为单轴抗拉强度；σ3为最大主应力。

介质发生剪裂的条件为：

(4)

(5)

式中：fs是剪裂屈服函数；σ1为最小主应力；c为黏聚力；φ为内摩擦角。

接触-摩擦模块被用于处理单元嵌入后的相互作用。引入势的概念计算接触力[10-11]，以避免法向接触力与接触面积无关的弊端，并使针对不同的接触类型的计算具有统一性。

势函数

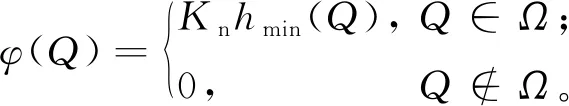
(6)

式中：Kn为法向刚度系数，Pa/m；hmin(Q)为单元内任一点Q距单元边界的最短距离，m；Ω为互嵌区域。

运动模块被用于计算节点的速度和位移。弹性力由单元应力计算得到；不平衡力是弹性力和外力(例如，自重和外部载荷)等力的合力；阻尼力与不平衡力呈线性关系，其比例系数为局部自适应阻尼系数。计算模式包括动力计算模式和准静力计算模式(模拟时间较长的开采过程)。在连续介质向非连续介质转化或非连续介质进一步演化过程中，一些不能再开裂的煤层单元会与周围单元发生相互作用，能承受超过自身承载能力的高应力。为此，提出了针对煤层离散单元聚集体的应力跌落方法，或者将煤层视为连续介质，仅对煤层单元在必要时进行应力跌落。

2 基于点-单元接触模式的水平岩层运动计算方法

拉格朗日元与离散元耦合方法仅适于模拟几万个单元数的采场模型的岩层运动过程，并不适于模拟10万个单元以上的情况，主要是受到微机计算速度的限制。例如，当岩层较为破碎时，由于存在大量的接触检测等原因，原接触-摩擦模块的用时较长。为此，需要研究水平岩层运动的并行计算方法，例如，借助图形处理器(GPU)进行加速。以接触-摩擦模块中的点-单元接触模式为例进行介绍。

如图2所示，采用点-单元接触模式取代单元-单元接触模式，以起到精简算法和适于GPU并行的目的。点即接触点，布置在单元的边上。在建模完成且开始计算前，建立盒子网络覆盖模型。盒子为宽度一致的正方形。在1个时步内，首先，将各接触点及与其可能发生接触的单元加入盒子；然后，对于每个盒子，将其中任一接触点和任一单元作为1组，对所有组合进行嵌入判断(每当有1组被判定为发生嵌入，则生成1个包含该组接触点和单元的接触对)；最后，计算接触对中接触点的接触力，将接触力及其反作用力进行分配，令接触对消亡。应当指出，在岩层运动过程中，当某一接触点与任一单元发生嵌入时，则1组包含该接触点和该单元的接触对生成；否则，接触对未生成。盒子宽度影响接触对数量和计算效率，盒子宽度过小会使部分接触无法被检索到，盒子宽度过大会增加不必要的计算量。考虑到单元会变形，根据经验选取盒子宽度。在接触-摩擦模块中，由设备端计算得出的单元和节点信息，进行接触判断，生成接触对并计算接触力，再将计算出的接触力分配给相应节点。给每个盒子分配1个线程，各线程同时计算，大大提高了计算效率。

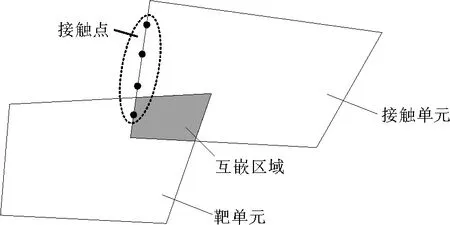
图2 接触单元上一条边的接触点

对于点-单元接触模式，当1个接触点嵌入1个单元时，该接触点上的接触力

F=0.5KnLAhn。

(7)

式中：L为该接触点所在边的长度；A为该接触点对应的求积系数；h为该接触点到被嵌入单元边界的最短距离；n为垂直于该接触点所在边的单位矢量，方向指向该接触点所在单元内部。将F分配至该接触点所在边两端节点，并将F的反力分配至被嵌入单元的4个节点。

显然，新接触力的计算比原接触力的积分计算简单。而且，当边上的接触点数量足够多时，两种方法将具有相同的精度。目前，在1条边上布置了4个接触点，接触点的坐标可由其所在边两端节点的坐标求得。

在水平岩层运动计算方法中，要求各岩层的厚度不变。在模型建立过程中，由下至上依次建立各岩层。通常，在模型的左、右两侧施加水平约束，在模型的下端面施加垂直约束，在模型的上端面施加垂直向下的均布载荷p。计算条件为平面应变、大变形。对于各岩层，主要的力学参数包括5个：弹性模量、泊松比、黏聚力、内摩擦角和抗拉强度。上述主要参数均可通过实验测得。对于煤层，还需要应力跌落系数。单元尺寸过大会导致计算结果精度较低，即模拟效果不好；单元尺寸过小会导致计算效率较低。根据经验，将单元边长取为0.5 m较为适合。这样，不需要引入I型和II型断裂能。应当指出，各岩层的相互作用通过相互嵌入实现，无需给任意两个相接触的岩层提供接触刚度。Kn为材料属性，而非界面属性，其大小与弹性模量成正比。比例系数的提高有利于减小嵌入量造成的误差。

3 岩层运动过程模拟

本研究模拟了3个采场模型的岩层运动，示意图见图3。模型1是新巨龙矿1302N工作面走向模型[15]，采用逐渐删除煤层单元的方式模拟煤层开采，推进方向位于纸面内且向右，每隔10 000个时步开采5 m。模型2是柠条塔煤矿S1201工作面侧向模型[16]，当N=50 000～950 000时，对右巷右方待采煤层的顶、底板进行卸压，卸压完毕相当于煤层开采完毕，左巷和右巷的高度等于煤层厚度，对右巷顶板进行了切缝，切缝角度为5°，同时，对右巷围岩进行等效支护(包括锚杆、锚索和液压支柱)，推进方向垂直于纸面。模型3是柳巷煤矿30105工作面侧向模型[17]，一次性开挖煤层，煤层中的左巷和右巷的高度小于煤层厚度，推进方向垂直于纸面。限于篇幅，仅在表1中给出了部分所需参数。

表1 3个采场模型的部分参数

图3 3个采场模型示意图

3.1 传统工法条件下走向岩层运动模拟

当N=80 000时(工作面推进距离D=30 m)(图4(a))，采空区上方的粉砂岩层3存在一个正V字形σ3高值区，采空区下方存在一个倒V字形σ3高值区，两个高值区均为拉应力；开切眼后方与工作面煤壁前方的煤层分别存在σ3较高区域，均为压应力，挤压程度较轻，前者宽度约为28 m，后者宽度约为15 m；关键层Ⅰ、Ⅱ之间的各岩层的σ3分布不均匀(例如，关键层Ⅱ下方的细粒砂岩层5的中性层上方的σ3较低，挤压较为严重)；关键层Ⅱ、Ⅲ的σ3分布较为均匀。

当N=160 000时(D=70m)(图4(b))，开切眼后方和工作面煤壁前方的煤层的σ3高值区的宽度分别为30和12 m；顶板存在大V字形的σ3高值区，为拉应力。开切眼附近出现1条向右上方发展的倾斜拉、剪复合裂纹(图中灰色、黑色线段分别代表拉裂纹、剪裂纹)，前期以剪为主，后期以拉为主，已贯穿关键层Ⅰ和细粒砂岩层2；采空区上方出现1条由下至上发展的拉裂纹，已贯穿关键层Ⅰ；关键层Ⅰ与其上岩层出现离层；开切眼后方的细粒砂岩层2出现1条由上至下发展的剪裂纹；工作面煤壁上方的泥岩层2出现若干条剪裂纹。

当N=240 000时(D=110 m)(图4(c))，采空区上方的关键层Ⅰ发生局部垮落，垮落区域尺寸达60 m；关键层Ⅰ与其上岩层的离层十分明显；开切眼前方悬露的关键层Ⅰ出现若干条剪裂纹，工作面煤壁后方悬露的关键层Ⅰ已出现若干条由上至下发展的近似平行的倾斜剪裂纹；采空区上方的离层向上发展至距离煤层上表面约101 m处；开切眼后方与工作面煤壁前方的若干岩层出现多条剪裂纹；采空区上方的关键层Ⅱ的裂纹较为稀疏；关键层Ⅲ出现1条由下至上发展和3条由上至下发展的拉裂纹，其中，2条由上至下发展的拉裂纹贯穿关键层Ⅲ，可能是由于模型水平方向仍不足够长且在模型左、右两端施加了水平约束。

当N=450 000时(D=110 m)(图4(d))，采空区上方的大部分离层已闭合；模型上表面发生明显沉降；开切眼前方的采空区空间缩小；工作面煤壁后方悬露的关键层Ⅰ已垮落；若干岩层出现更多拉裂纹和剪裂纹，越向上，裂纹越向模型左、右边界发展，这导致裂纹的分布在整体上呈上底长下底短的梯形。此后，裂纹的分布形态基本不变，各岩层处于稳定状态。

图4 模型1的σ3的时空分布(单位：Pa)

3.2 110工法条件下侧向岩层运动模拟

当N=40 000时(巷道的开挖、支护及顶板切缝均已完成，尚未开采)(图5(a))，两巷的顶、底板均出现垂直拉裂纹，与左巷相比，右巷顶板的裂纹更少，这是由于对右巷进行了支护；拉裂纹尖端、切缝尖端和切缝右下方存在σ3集中；两巷两帮的σ3较高，左巷左、右帮的σ3较高区域的宽度分别为13和14 m；右巷左、右帮的σ3较高区域的宽度分别为4和14 m；在粉砂岩层与石英砂岩层中，两个相连的V字形σ3高值区有形成的趋势，但切缝的存在使右V字形σ3高值区右半部分基本消失；两巷底板均存在倒V字形σ3高值区；远离巷道的煤层的σ3最低，这是由于煤层的泊松比最大，导致其水平变形最大，且模型左、右边界被施加水平约束。应当指出，上述σ3高值区内均为拉应力。

当N=120 000时(图5(b))，两巷之间的煤柱上方和左巷左方的粉砂岩层和石英砂岩层存在σ3集中，挤压较为严重；左巷左方煤层和煤柱上方的中砂岩层和松散岩层处于拉应力区，出现由上至下发展的拉裂纹；远离右巷的右方粉砂岩层和石英砂岩层处于拉应力区，出现由下至上发展的拉裂纹。

当N=800 000时(图5(c))，在石英砂岩层、中砂岩层和松散岩层中，煤柱和左巷左方煤层的上方出现更多拉裂纹，且各岩层下部分出现成片的剪裂纹；右巷右方的岩层出现众多裂纹：由下至上形成了许多近似等间距的拉裂纹，由上至下形成了成片的剪裂纹。在粉砂岩层中，煤柱上方出现成片的剪裂纹；右巷右方出现若干近似平行的拉裂纹。而且煤柱下方的底板出现成片的剪裂纹；右巷右方的岩层发生少许沉降；由切缝尖端已经发展出裂纹。

当N=1 200 000时(待采煤层已被开采，采空区已形成)(图5(d))，由切缝尖端发展出的裂纹促进了采空区上方的部分岩层垮落，右巷右侧形成矸石帮，使巷道得以保留；煤体向右巷的挤入现象明显，右巷顶板发生一定程度的下沉；在石英砂岩层、中砂岩层和松散岩层中，左巷左方煤层上方的裂纹变化不大，采空区上方出现更多的拉裂纹和剪裂纹，上述两个区域之间的裂纹有所发展；采空区上方的各岩层发生明显沉降。

图5 模型2的σ3的时空分布(单位：Pa)

文献[12]采用非连续方法UDEC呈现了顶板的垮落与离层。模型2的结果不仅出现了上述现象，还呈现了拉、剪裂纹的时空分布。

3.3 传统工法条件下侧向岩层运动模拟

当N=40 000时(图6(a))，采空区左方和右方的细砂岩层1分别存在一个σ3低值区，挤压较为严重，宽度分别为30和32 m。上述两个区域上方的细砂岩层1出现3条较长的由上至下发展的拉裂纹；采空区上方的细砂岩层1出现7条由下至上发展的拉裂纹；细砂岩层1、泥质砂岩层3及其之间的岩层出现大量倾斜拉裂纹和少量剪裂纹；采空区上方部分岩层发生少许冒落。

当N=800 000时(左、右巷道开挖已完成)(图6(b))，采空区左方和右方的细砂岩层1与泥质砂岩层3之间的岩层出现大量拉裂纹和剪裂纹：越靠近模型的左、右边界，裂纹越垂直；采空区上方的岩层出现密集的拉裂纹和剪裂纹，而且，成片的剪裂纹出现在某些岩层(例如粗砂岩层)的上部；顶板已冒落，大部分采空区已闭合；采空区左方和右方的巷道顶板均有所沉降；左巷右帮和右巷左帮的煤体向采空区鼓出；沙土层上表面明显弯曲，伴随着少量拉裂。

当N=1 200 000时(图6(c))，左巷顶板发生明显沉降，煤体向两巷内的挤入现象明显；两巷的顶、底板以及两帮均出现少量剪裂纹，左巷右帮和右巷左帮的煤体向采空区的鼓出更加明显；采空区上方的冒落带和裂缝带呈上底短下底长的梯形，而模型中裂纹的分布在整体上呈上底长下底短的梯形。此后，模型基本处于平衡状态。

图6 模型3的σ3的时空分布(单位：Pa)

采用连续方法FLAC3D，文献[13-14]均呈现了采空区上方的上底短下底长的梯形塑性区。模型1和模型3的结果不仅呈现了采空区上方的上底短下底长的梯形的冒落带与裂隙带，还呈现上底长下底短的梯形裂纹分布形态，这与文献[15-17]中的结果(导水裂隙带中的拉裂纹集中在采空区上方和开采边界，而剪裂纹多分布在开采边界外侧)定性相符。

4 结论

在拉格朗日元与离散元耦合方法的基础上，发展了水平岩层运动计算方法，采用点-单元接触模式取代单元-单元接触模式，以起到精简算法和适于GPU并行的目的。在传统工法条件下走向和侧向岩层运动模拟中，随着时步数目的增加，若干岩层不断开裂，岩层之间的离层在水平和垂直方向上不断发育，上覆岩层破断会导致下方的离层和采空区闭合。最终，裂纹的分布在整体上呈上底长下底短的梯形，这与导水裂隙带等的现场观测结果一致。在110工法条件下侧向岩层运动模拟中，采空区形成后，由右巷顶板切缝尖端发展出的裂纹促进了采空区上方部分岩层垮落，右巷右侧形成了矸石帮，使其得以保留。

本方法适于模拟采场模型的岩层运动过程，例如，岩层的变形、开裂、离层、破断和冒落等，还适于研究多种载荷(静水压力和冲击波等)条件下巷道围岩模型的破坏，例如，围岩开裂和坍塌以及岩块弹射等，具有需要参数少且参数容易获取的特点。