塔式太阳能熔盐吸热器光-热-力耦合模拟及性能分析
贾朋森,王 坤,张 翔,杨 历,闵春华
(1.河北工业大学 能源与环境工程学院,天津 300401;2.河北工业大学 热能科学与能源清洁利用河北省重点实验室,天津 300401)
0 引言
外露式吸热器因其耐高温、结构简单的优点成为塔式太阳能发电系统中最具发展前景的吸热器形式之一。然而,塔式太阳能热发电(Solar Power Tower,SPT)系统所聚焦太阳能流在吸热器表面分布极不均匀,这也对吸热器安全高效运行提出了挑战[1-2]。局部过热导致外部吸收涂层的退化和内部传热流体的分解[3-4];温度梯度过大将会使导致吸热管道较大的热应力和热变形,甚至造成吸热器结构故障[5-6]。
Du等[5]和Marugán-Cruz等[7]在吸热管表面热流密度遵循余弦分布的假设条件下分析了吸热管的应力特性,探讨了单管的应力分布与能流密度的关系,指出最大热应力位于吸热管能流密度最高处。Sánchez等[8]进一步在每个吸热管排中选取一根吸热管并进行串联,研究了整个吸热器中熔盐温度的变化及吸热器周向应力变化。Xu等[9]则对整个吸热器的热效率和表面温度随质量流量和DNI(Direct Normal Irradiation)的变化进行了研究。在他们的研究中,通过引入经验关联式来计算吸热器与外界环境的对流换热损失,忽略了对流换热系数沿吸热器周向的变化。随后,Christian等[10]和Uhlig等[11]提出将吸热管排简化成矩形的通道管板,并且通过引入风域计算吸热器与外界环境的对流换热损失,但由于将吸热管排简化为管板,未能对吸热管排的热应力进行分析。Wang等[12]基于蒙特卡洛光线追踪法(Monte Carlo Ray Tracing,MCRT)、有限体积法(Finite Volume Method,FVM)和有限元法(Finite Element Method,FEM)建立了太阳能吸热器的光-热-力耦合模型,研究了不同位置吸热管在不同时刻和热流密度下的光热转换性能及应力特性。
本文在前人研究方法的基础上,基于MCRT、FVM、FEM建立了外露式太阳能吸热器的光-热-力耦合数值模型,并通过与美国Solar Two电站的实验数据进行对比完成了模型验证,在此基础上探讨了在非均匀热流边界及外部强制对流换热条件下吸热器的光热转换性能及应力特性,重点讨论了多点聚焦下吸热器温度场的时空变化规律及应力分布。
1 计算模型及熔盐物性
1.1 物理模型
本文以Solar Two塔式熔盐电站采用的圆柱形外露管式吸热器为例进行分析。吸热器以熔盐Solar Salt作为吸热工质,包括2个熔盐回路,每个回路包括12个串联的吸热管排,如图1所示。吸热管的表面涂有黑色Pyromark选择性吸光涂层[13]。表1给出了吸热器物理模型的详细信息。图2给出了详细的熔盐流动路径、管排编号和吸热管编号。在回路1中,低温熔盐首先从编号为W1的管排入口流入,流经管排W6,再从管排W6出口流出,进入管排E7,最后从管排E12流出,如图1中红色回路线所示。回路2的熔盐流动方式与回路1类似。
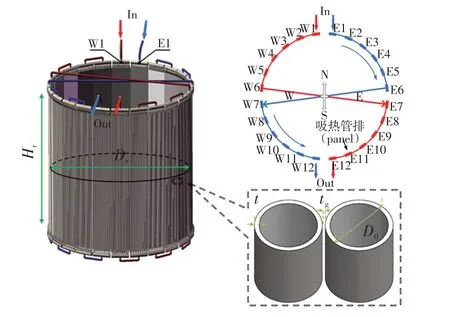
图1 Solar Two吸热器示意图(左侧),带有面板编号的流动回路图和管道细节(右侧)Fig.1 Schematic diagram of Solar Two receiver(left),and the flow circuit diagram with panel numbers and tube details(right)

表1 Solar Two圆柱形吸热器的几何参数Tab.1 Geometric parameters of Solar Two receiver
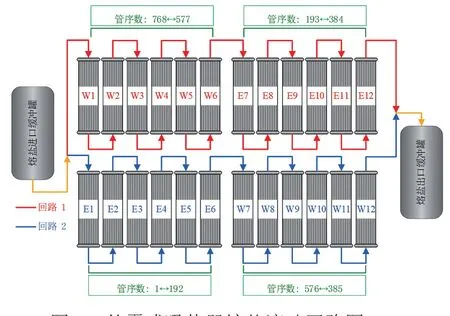
图2 外露式吸热器熔盐流动回路图Fig.2 Molten salt flow circuit diagram
1.2 定日镜场
定日镜场由2 111个定日镜组成,其方位和坐标如图3所示。每个定日镜宽4 m,高4 m,类型为球面镜。跟踪误差和斜率误差均为0.001 rad。此外,采用文献[14]中的多点聚焦瞄准策略,以减少吸热器上的峰值太阳能流密度。
1.3 熔盐及管壁物性
吸热器内传热流体采用传统的太阳盐(由40%的KNO3和60%的NaNO3组成)。熔盐物性参数[15]见表2。考虑到下一代吸热器对高温、高压和耐腐蚀性提出了更高需求,采用Haynes 230合金作为吸热器管壁材料[16],其性能参数见表3。

图3 定日镜场位置坐标图Fig.3 Heliostat field position coordinate diagram
2 数值方法及模型验证

表2 熔盐的物性参数[15]Tab.2 Physical parameters of molten salt
2.1 数值方法
数值计算模型包括光学模型、传热模型和应力模型。
在光学计算中,采用MCRT方法准确获得了全镜场条件下塔式太阳能吸热器表面非均匀的能流分布。将吸热器表面划分成多个吸热单元,通过计算吸热器上每个网格所吸收的太阳能通量来计算吸热器接收的总太阳能通量。网格单元吸收的太阳能(Qe)由式(1)计算。入射到吸热器表面的总太阳能(Qi)由式(2)计算:

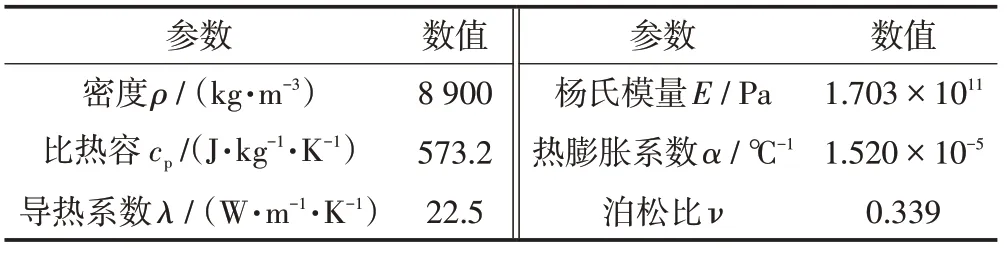
表3 Haynes 230合金的热性能和力学性能Tab.3 Thermal and mechanical properties for Haynes 230 alloy
式中:Esunray是每个太阳光束所携带的能量,W;nsunray是每个网格单元所接收的太阳光束;Ne是吸收太阳能的网格单元总数。
光学效率定义为吸热器表面接收的能量与定日镜场所接收的太阳辐射能量之比,由式(3)计算:

式中:DNI为直接法向辐照度,W·m-2;nh是定日镜的数量;Lh和Wh分别是每个定日镜的长度和宽度,m。
传热过程采用FVM进行计算。吸热器表面接收的太阳能部分用于加热低温熔盐,另外一部分能量则通过辐射、对流、导热等方式散失到外界环境。计算中包含的控制方程如式(4)~(11)所示。
连续性方程:

动量方程:
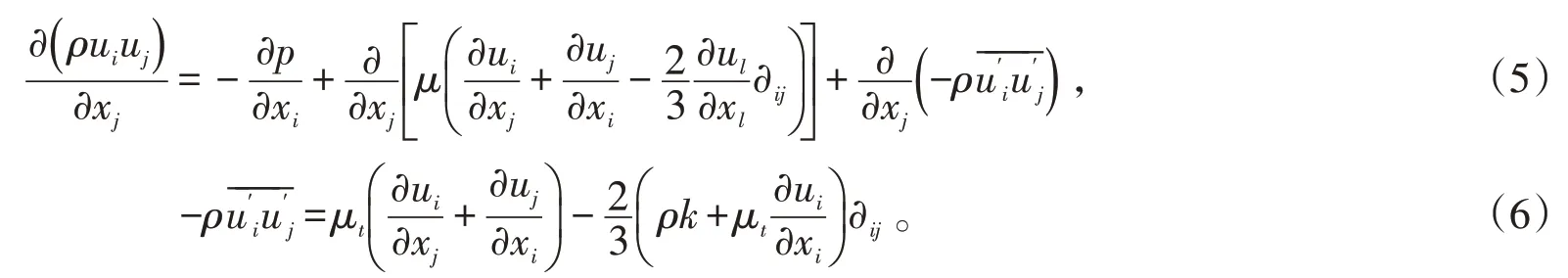
湍流计算选用标准k-ε湍流模型,近壁面处理采用标准壁面函数,具体描述如下:
k和ε方程:
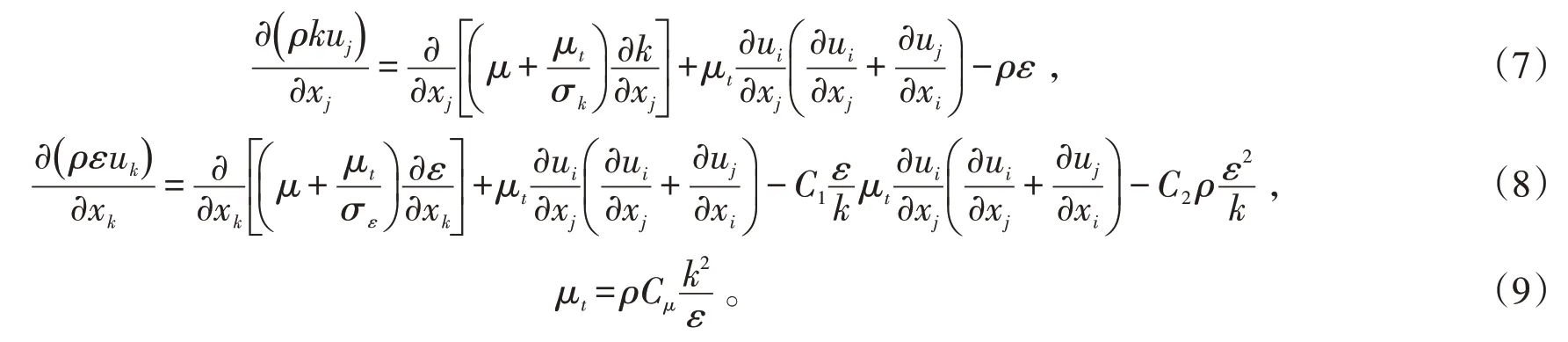
能量方程:

辐射计算采用DO辐射模型,辐射传递方程为

式中:μ和μt分别是动力黏度和湍流粘度,Pa·s;σk、σε、C1、C2和Cμ是常数,分别为1.0、1.3、1.44、1.92和0.09;u为速度,m·s-1;ρ为密度,kg·m-3;p为压力,Pa;cp为工质的定压比热容,J·kg-1·K-1;I是辐射强度,W·m-2;和分别是空气中的位置向量和方向向量。
吸热器热效率(ηthe)定义为:
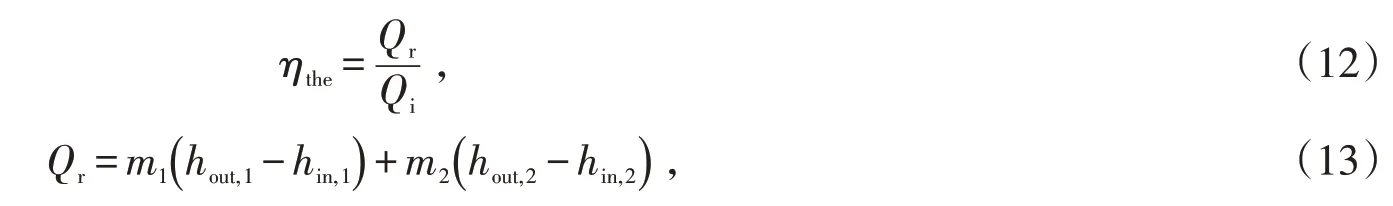
式中:Qi是吸热器表面的入射太阳能,W;Qr是熔盐吸收的热能,W;其中m是熔盐的质量流量,kg·s-1;h是熔盐的焓值,kJ·kg-1;下标“1”、“2”、“in”和“out”分别代表流路1、流路2、流路入口和流路出口。
光热转换效率(ηot)定义为定日镜场的光学效率(ηopt)和吸热器热效率(ηthe)的乘积,计算公式为

静态结构模型计算方法是将传热模型计算得到的温度和压力加载到管道中,利用FEM计算管道的应力和应变。吸热管被认为是具有各向同性物理特性的热弹性体。热弹性的基本方程包括平衡微分方程、应变-位移方程和本构方程。在圆柱坐标系中这些方程表示如下。
平衡微分方程:
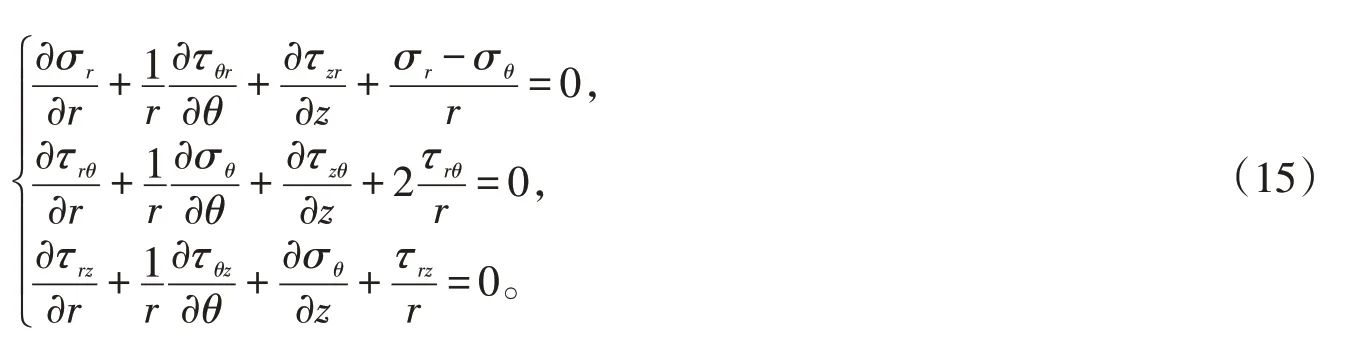
根据等效剪切应力定理,忽略体力,可得如下关系:

应变-位移方程:
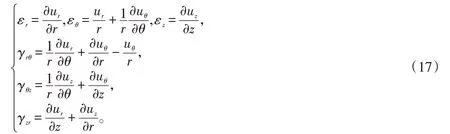
热弹性本构方程:
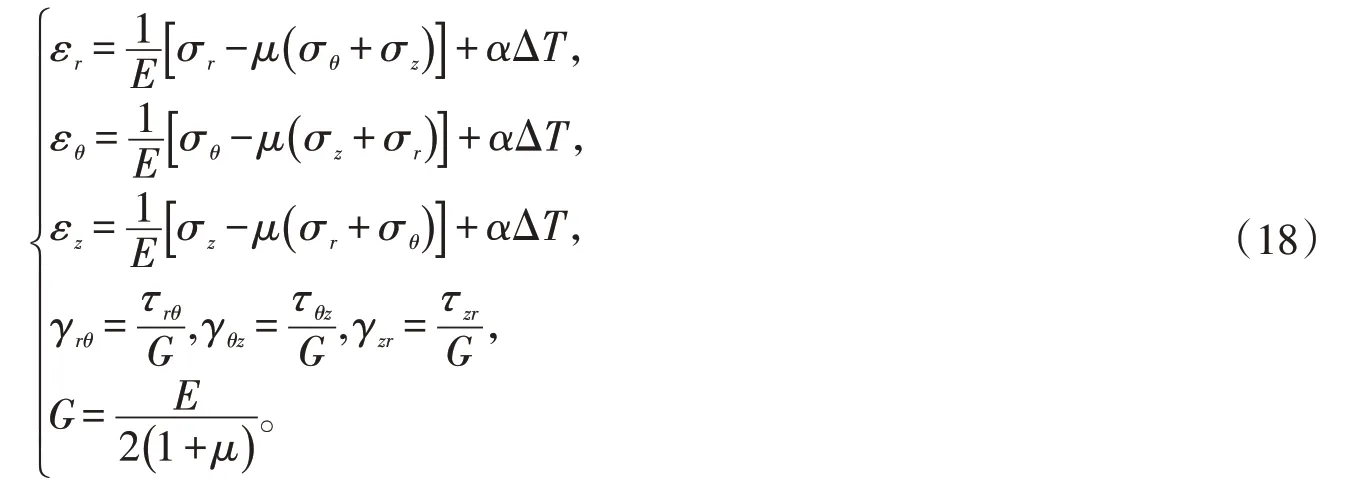
式中:E是杨氏模量,Pa;μ是泊松比;α是热膨胀系数,K-1;ΔT是温升,可以从热流体计算模型中获得;G表示剪切模量,Pa。
Von Mises理论定义的等效应力公式为
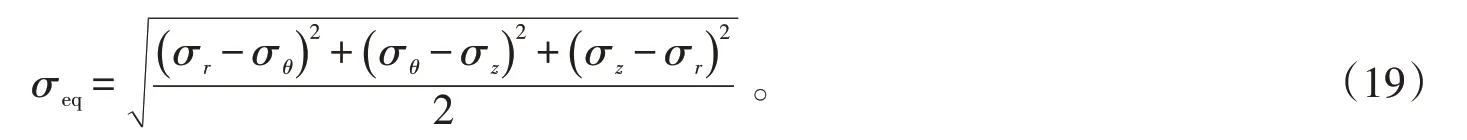
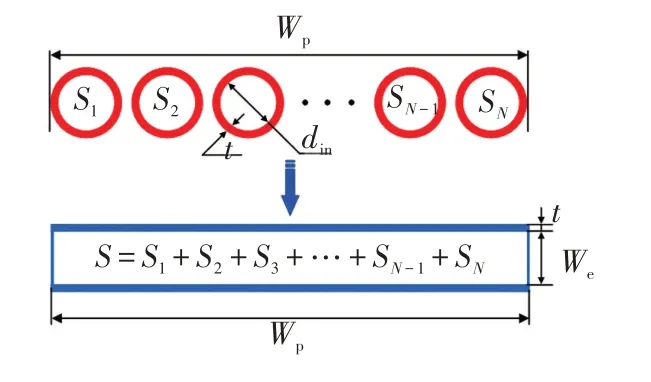
图4 简化的面板模型Fig.4 Simplified panel model
以光学模拟得到的太阳能通量作为传热模型的热边界条件。为了节省计算资源,提高计算速度,基于Christian[10]和Uhlig[11]的研究方法,将管板简化为矩形板,如图4所示。平板与实际吸热器面板相同。矩形面板的横截面积等于面板中所有管道的横截面积之和,以保证相同的流速。因此,矩形面板的流体通道等效宽度(We)为12.9 mm。矩形面板的壁厚(t)与管道的壁厚(t)相同,以保持相同的热传导。图5显示了传统外露式太阳能吸热器的换热模型边界条件。吸热器周围是一个圆柱形空气区,其直径比吸热器大5倍,高度相同。空气域左侧为速度入口边界。空气域的其他边界条件设置为压力出口。吸热器面板两侧均视为绝热薄壁,入口和出口边界条件分别为质量流入口和压力出口。外露式吸热器外壁面接收太阳能辐射,内壁面设置为绝热。UDF自编程用于计算前一个吸热器管排的出口温度,并将其分配给下一个吸热器管排的入口温度。计算过程采用二阶迎风离散控制方程。

图5 外露式吸热器的边界条件Fig.5 Boundary conditions for cylinder external receiver
在对熔盐吸热器进行局部单根吸热管的热力计算时,流动换热计算和上文中简化管排的边界条件保持一致。管道半侧受热,将光学计算的该管道处的热流通过UDF以体热源的方式加载在受热壁面。表面对流换热系数由简化模型计算得出。入口和出口边界条件分别为质量流量入口和压力出口,流动方向参照图2。质量流量的大小为管排总进口流量的1/32。力学模型的边界条件定义如下:1)管道外表面与大气环境接触,因此外壁面边界为标准大气压0.1 MPa;2)熔盐在管道中流动时,内壁承受压力为2 MPa;3)为实现自由膨胀,管道两端采用弱弹簧边界条件[17]。
2.2 网格独立性验证及模型验证
选取以下工况为例进行网格独立性验证:春分日12时,西风风速1.0 m/s,环境温度为18℃,熔盐入口质量流量为45 kg/s,熔盐入口温度为573.15 K。流体壁面附近网格的细化y+值均在30左右,满足标准壁面函数y+值大于15的要求。如图6所示,当网格数量为691.2万时,出口温度Tout和热效率ηthe的变化趋于稳定。因此,本文选取此网格划分方法,足以保证计算的准确性。为了验证本文数值方法的准确性,将模拟结果与美国Solar Two电站的实验数据进行了对比。对比过程中保持一致的边界条件。图7显示了计算结果与实验结果之间的比较。可以看出,计算结果与实验结果吻合较好,最大误差为1.3%,说明数值模型是可靠的。
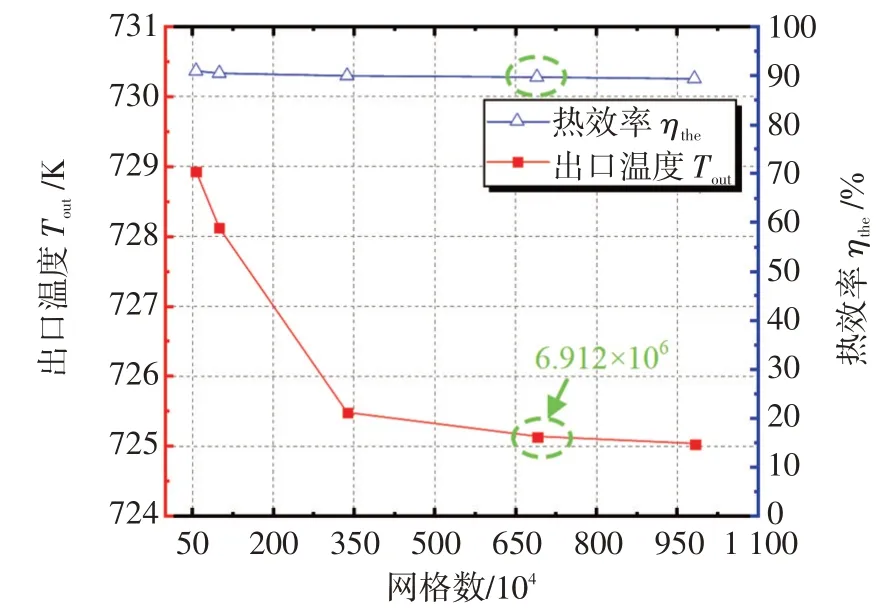
图6 外露式吸热器的网格独立性验证Fig.6 Grid independence verification for cylinder external receiver

图7 实验数据与计算结果之间吸热器效率比较Fig.7 Comparison of the receiver efficiency between the experimental data and calculated results
3 结果与分析
3.1 太阳能流分布及光学性能
太阳辐射强度与太阳位置随时间变化而变化,这对吸热器的性能同样会产生较大影响。图8a)、b)、c)分别给出了春分日当地太阳时8:00、12:00、16:00时吸热器表面能流分布情况。由于北半球的塔式太阳能光热发电站北侧布置更多的定日镜,因此吸热器北侧的能流密度高于南侧。上午8时东西两侧的能流密度表现出明显的不均匀性,西侧的辐照范围W4~W9远大于东侧的辐照范围E4~E9。最高能流密度为456.4 kW/m2。正午12时吸热器东西两侧的入射能量分布基本对称,最高能流密度达到一天之内的峰值620.3 kW/m2。与上午8时相反,下午16时东侧的辐照范围E4~E9远大于西侧的辐照范围W4~W9。由此可见随着太阳方位角和高度角的变化,一天中吸热器表面太阳能流密度由西侧向东侧偏移,南北两侧能流密度的分布差异变化较小。
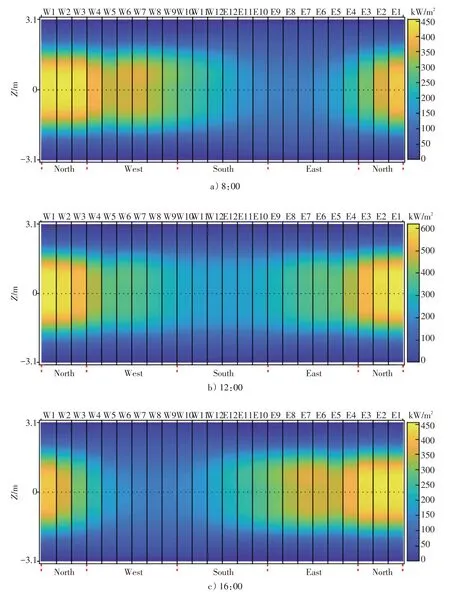
图8 春分日不同时刻热流密度分布Fig.8 Distribution of heat flux density at different times on the vernal equinox
图9展示了外露式吸热器在春分日不同时刻的光学效率ηopt随DNI的变化图。从图中可以看出,上午光学效率随着DNI的逐渐增加而增大,正午12时达到最大辐照度,因此光学效率达到最大值。下午光学效率逐渐降低并与上午相同太阳高度时的光学效率保持一致。结果表明,光学效率的变化与DNI的变化具有伴随性。
3.2 外露式吸热器的热性能
本节分析了不同时间和天气条件下外露式吸热器光热转换性能。
选取春分日西风风速1.0 m/s,熔盐进口温度300℃,出口温度565℃的工况为例进行分析。图10为晴天条件下,外露式太阳能吸热器热效率和光热转换效率随当地太阳时ts的变化。可以看出,一天内外露式吸热器的热效率ηthe随ts先增大后减小,在正午12时达到最大值83%,光热转换效率ηot同样达到峰值58.5%。吸热器所截获的太阳能随着光照强度先增后减,在正午12时达到最大值,由于额定出口温度保持不变,高热流密度致使吸热器内熔盐质量流量增加,熔盐与管壁的对流换热增强,此时吸热器热效率达到峰值,光热转换效率也随之达到峰值。
吸热器外壁面的强制对流同样对吸热器换热性能有着重要影响。图11所示为外露式吸热器外壁面对流换热系数。从整体上看,吸热器外壁周向对流换热系数受风向的影响较大。西侧属于迎风侧,图中可以明显看出西侧管壁的对流换热系数大于东侧(背风侧)管壁。同时,由于低温熔盐从北侧近入,吸收高温热流后从南侧流出,所以吸热器北侧管壁温度较低,南侧管壁温度偏高,故南侧比北侧具有较高的对流损失。
图12展示了春分日正午12时吸热器热效率和光热转换效率随风速的变化。当西风风速由1 m/s增加到20 m/s时,吸热器的热效率ηthe由83%降低至71%,光热转换效率ηot由58.4%降低至50%。并且随着风速逐渐增大,热效率降幅更加显著。这是由于外露式吸热器的暴露面积较大,在较大风速下产生了较高的对流损失。
图13为春分日正午12时外露式吸热器外壁面的温度分布云图。Y轴的正方向为正北,X轴的正方向为正东。在吸热器的周向上,南侧管排的温度明显高于北侧管排,且峰值温度为890.96 K,出现在最南侧管排上。可见温度也表现出强烈的非均匀性,且与图8b)所示的表面热流密度分布恰好相反。出现这种现象的原因可归结于吸热器熔盐的流动布置方式。在此布置方式下,熔盐从最北侧高热流密度区进入,由于低温熔盐和高热流密度的壁面温差较大,换热能力较强。在由北向南流动的过程中,熔盐吸热,温度逐渐升高,而管壁太阳能流密度逐渐降低,换热逐渐趋于缓慢,吸热管壁温度与熔盐温度变化趋势一致。在北侧入口附近,由于低温熔盐从高热流密度区进入,避免了该区域峰值温度过高;在南侧出口附近,由于南侧太阳能流密度较小,熔盐温度较高,甚至会出现熔盐向外放热的现象。这些现象能够在一定程度上降低吸热管壁的最高温度,提高吸热器的安全性能。

图9 外露式吸热器春分日不同时刻的光学效率和DNIFig.9 Optical Efficiency and DNI of cylinder external receiver at different times of the spring equinox
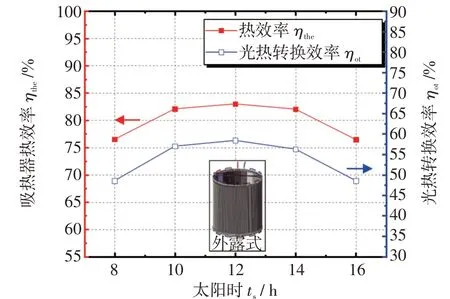
图10 外露式吸热器春分日不同时刻的热效率和光热转换效率Fig.10 Thermal efficiency and photothermal conversion efficiency of cylinder external receiver at different times of spring equinox

图11 外露式吸热器春分日12时外壁周向对流换热系数Fig.11 Circular convective heat transfer coefficient of outer wall of cylinder external receiver at 12:00 on spring equinox
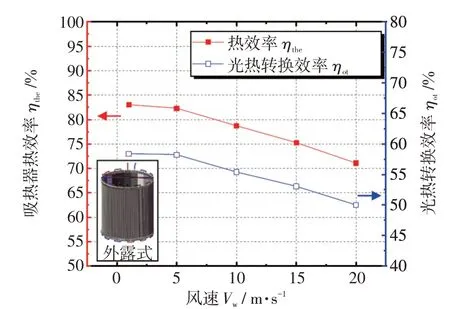
图12 外露式吸热器不同风速的热效率和光热转换效率Fig.12 Thermal efficiency and system photothermal conversion efficiency of cylinder external receiver at different wind speeds
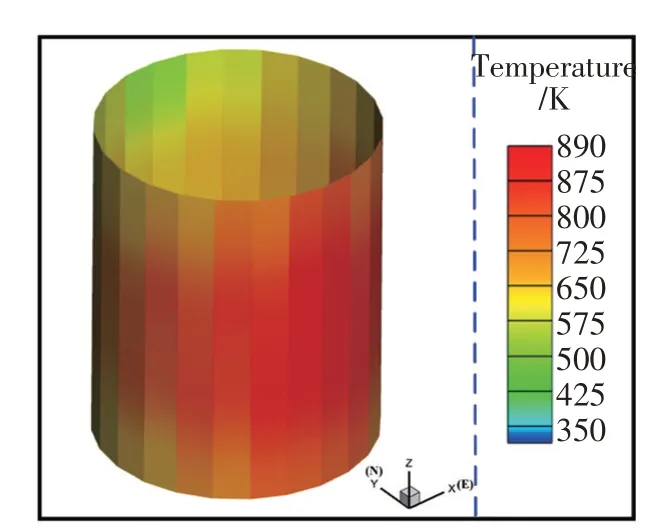
图13 外露式吸热器温度分布云图,春分日正午12时,Tmax=890.96 KFig.13 Cloud chart of temperature distribution of cylinder external receiver at 12 noon on the spring equinox,Tmax=890.96 K
3.3 外露式吸热器的应力分析
上文中已经获得了典型工况下熔盐吸热器的太阳能流密度,以及整体和局部的温度分布,发现不均匀的能流分布是造成温度分布不均的主要原因。温度分布不均和局部热点,给吸热器结构和寿命带了较大的安全隐患。因此本节针对吸热器在典型工况真实能流分布下的整体及局部的应力特性进行了探讨。
图14为吸热管的温度分布和综合应力分布。如图所示,综合应力沿轴向分布与温度分布趋势相同,在管道中部达到峰值。在圆周方向看,高能流密度区吸热壁面的热应力也高于低能流密度区吸热壁面,但峰值位于吸热器高能流密度区与低能流密度区交界处,这是因为此位置的温度梯度最大,应力集中明显。这一点可以从图15管道的中间截面处更清楚地看出。
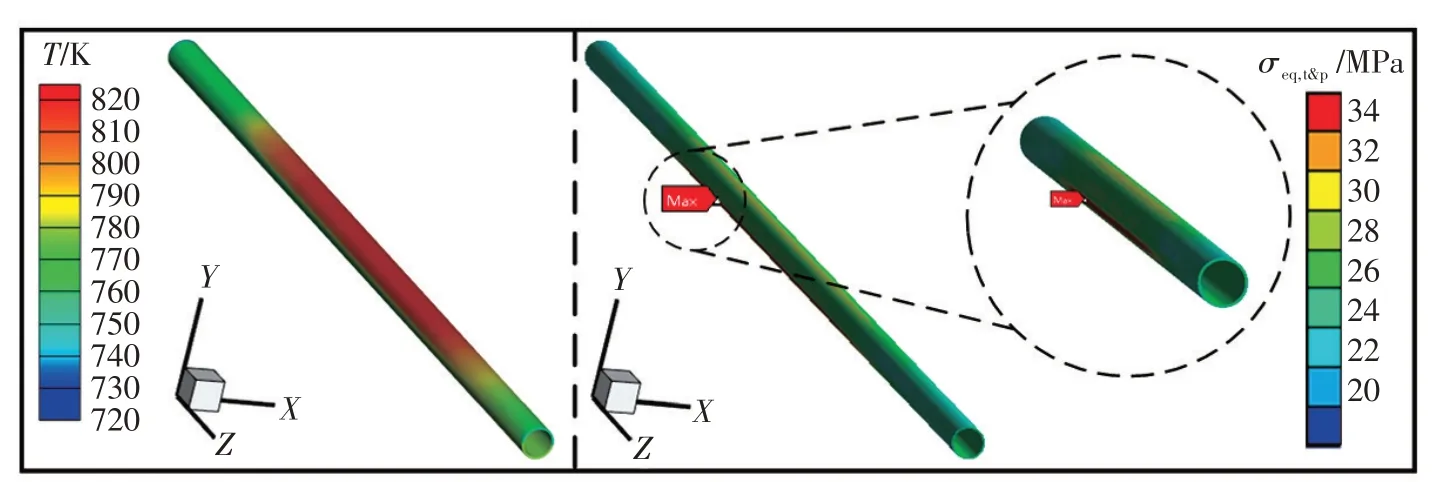
图14吸热管温度分布和应力分布,管排E8,管道241Fig.14 Temperature distribution and stress distribution of heat absorber tube,panel E8,tube 241
图15 为吸热管中间截面的综合应力、压应力、热应力分布云图。从图中可以清楚地看出,温度梯度导致的热应力与操作压力导致的压应力在数量级上是一致的,但在分布上有很大的不同。压应力在吸热器管道内壁面达到峰值,并由内壁面向外壁面沿径向逐渐减小;而热应力峰值出现两侧中间偏下区域。综合应力是由温度梯度和压力共同造成的,其分布是热应力和压应力分布的综合体现。
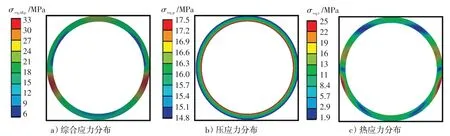
图15 吸热管E8-241中间截面(Z=3.1 m)的综合应力、压应力、热应力分布Fig.15 Distribution of comprehensive stress,compressive stress and thermal stress in the middle section(Z=3.1 m)of heat absorber tube E8-241
图16展示了各个吸热管排中间管道的最大综合应力,通过此图来分析整个吸热器的应力分布。可以看出综合应力的变化趋势与热流分布完全一致,高能流密度区的吸热壁面热应力远高于低能流密度区吸热壁面。产生这种现象的根本原因在于壁面温差,正午12时管排E1~E6和W1~W6表面热流密度高,但熔盐温度较低,因此内外壁面温差大,产生较大的综合应力。从选取的单管来看,峰值应力52.48 MPa正是出现在管排E1中间管道上,管排E1能流密度及壁面温差最大。最低应力28.87 MPa在管排E12处中间管道上,管排E12能流密度及壁面温差均为最小。峰值应力与最小应力相差近2倍。由此可以看出,即使在多点聚焦瞄准策略下吸热管外侧热流分布相对均匀,但吸热管内外侧受热不均的问题仍然存在,受光侧和背光侧较大温差仍会产生较大的局部应力。未来的研究应着重解决外露式吸热器单侧受热问题。
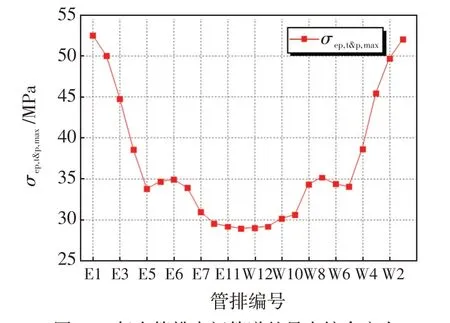
图16 每个管排中间管道的最大综合应力Fig.16 Maximum equivalent stress of the middle pipe of each panel
4 结语
本文结合MCRT、FVM、FEM建立了基于传统的外露式太阳能吸热器全尺寸的光-热-力耦合数值模型,探讨了不同日期和非均匀太阳能流分布对吸热器热性能的影响,并进一步分析了多点聚焦瞄准策略下单侧受热吸热器的热应力特性。得出以下主要结论:
1)随着太阳高度的变化,吸热器一天中集中热流密度由西部向东部偏移,南北两侧热流密度的差异变化较小。光学效率的变化与DNI的变化具有伴随性。
2)正午时刻的高热流密度致使吸热器内部流体传热增强,因此吸热器热效率和光热转换效率均达到最大值。吸热器效率受风速影响较大,且迎风侧对流换热系数较大,带来较高的热损失。
3)吸热管壁中间温度较高,进出口位置温度较低,并且由于单侧受热,受光侧和背光侧温差较大,交界处产生较大的集中应力。管壁的综合应力由热应力占主导。
4)全尺寸吸热器综合应力的变化趋势与热流分布基本一致,高能流密度区的吸热壁面热应力远高于低能流密度区吸热壁面。峰值应力与最小应力相差近2倍。由此可以看出,即使在多点聚焦瞄准策略下吸热管外侧热流分布相对均匀,传统的外露式吸热器由于单侧受热仍会产生较大局部应力。

