受端混联型LCC⁃VSC直流侧谐波计算方法研究
叶键民,王若愚,罗红梅,谢岩
(1.深圳供电局有限公司,广东 深圳 518000;2.中国电力科学研究院有限公司,北京 100192)
相比于交流输电,直流输电方式具有线路造价低、输送容量大、可以实现不同频率电网之间的联网、无同步稳定性问题等优势,在几十年间得到了长足的发展[1-2]。目前在实际工程中使用的高压直流输电技术主要包括两种:基于电网换相换流器的高压直流(line commuted converter based high voltage direct current,LCC-HVDC)[3-4]输电技术和以全控型器件为基础的电压源换流器高压直流(voltage source converter based high voltage direct current,VSC-HVDC)[5-7]输电技术。
LCC-HVDC具有结构简单、造价低、技术成熟、可靠性高以及适合远距离大容量电能传输等诸多优势[8]。但LCC换流站在工作时需要吸收大量无功功率,且交直流侧均含有大量谐波,需要额外的无功补偿以及交直流滤波装置,增大了建设成本。文献[9]采用基于开关函数的谐波计算模型对LCC-HVDC特征谐波进行分析,指出LCCHVDC直流侧谐波分量以12,24,36,48次直流电压特征谐波分量为主。同时,LCC-HVDC受自身技术限制,在逆变侧存在换相失败问题,无法向弱交流系统/无源网络供电[10-11]。相比之下,VSCHVDC采用全控型电力电子器件IGBT,再结合电压调制技术,能够独立调节有功功率与无功功率,谐波水平低,可以向无源网络供电,不存在换相失败问题,并且占地面积小,有助于清洁能源接入网络[12-13]。
综合来看,LCC-HVDC和VSC-HVDC都有各自的优势和不足,为了能充分发挥两种直流输电方式的优势,在同一直流系统中使用这两种不同类型的换流器,称之为混合直流输电技术[14-15]。混合直流输电系统有多种不同的拓扑结构,如整流侧LCC逆变侧VSC结构、整流侧LCC逆变侧LCC和VSC串联结构、1条LCC-HVDC和1条VSC-HVDC混合连接结构等[16-17]。国家电网公司规划的白鹤滩—苏南的混合直流输电工程也是混合直流输电方式的一种,它是一种受端混联型直流输电系统,即直流输电系统的整流侧采用LCC,而逆变侧则采用高压阀组LCC与低压阀组三端并联VSC相串联的结构。采用这种结构的优势有:相较于LCC结构,逆变端低压阀组的VSC可以在一定程度上降低系统在逆变侧发生换相失败的几率,显著减少了线路上的无功传输以及功率损耗,减少了无功补偿装置和滤波环节的投入,提高了经济性,并且在主直流线路故障时高压阀组LCC可以起到故障隔离的作用。相较于VSC结构,混联结构的传输容量更大,制造难度低,造价低。除此之外,受端采用多端口并联的形式可以让电能的传输与出口的设置根据实际需要进行调整,使直流系统变得更加灵活[18-19]。
这种新型拓扑结构的直流侧谐波特性对整个受端混联型LCC-VSC系统的控制保护有比较大的影响[20],目前很少有文献对该系统直流侧谐波特性展开研究和讨论。针对这个问题,本文首先研究LCC-HVDC直流侧不同频次谐波电流通路及其等效模型,其次研究VSC直流侧谐波等效模型,然后提出受端混联型LCC-VSC系统直流侧谐波的定量计算方法,最后利用实例模型验证所提方法的正确性和有效性。
1 LCC-HVDC直流谐波等效模型
混联型LCC-VSC系统中,LCC以12脉动换流器为输电单元。12脉动LCC换流器输出直流电压主要包含12k次谐波分量(k为整数,一般小于10)。然而在实际运行直流输电工程的接地极电流中检测到了较高的6k+3次谐波分量,经分析发现,换流变压器与地之间的杂散电容导致了接地电流支路的产生,而该支路在极线与接地线的谐波电流分布中起了相当重要的作用。从而,在现有的直流侧谐波分析方法中,一般将12脉动LCC换流器用3脉动谐波电压源等值,如图1所示。

图1 12脉动LCC换流器的3脉动谐波电压源等值电路Fig.1 Equivalent circuit of 3-pulse harmonic voltage source for 12-pulse LCC converter
图1中,12脉动LCC是由4个3脉动谐波电压源串联组成,每个3脉动谐波电压源相位相差π/6。以3脉动谐波电压源及其参数为基本单元,C3p为耦合于变压器绕组和地之间的杂散电容,其典型取值为10~20 nF,L3p为串联在谐波电压源的等值电感。由于常见的LCC换流器为6脉动换流器,每隔π/3电角度发生一次换相,且换相过程中的换相电感为换流变压器漏感的1.5倍(不换相时为换流变压器漏感的2倍),所以用6脉动换流器参数来计算L3p。3脉动谐波电压源等值电感L3p是6脉动LCC换相电感平均值的1/2,可以表示为

式中:μ为换相重叠角,rad;LT为换流变压器漏感。
假定12脉动LCC输电单元中星/星形接线方式的变压器二次侧电压为

式中:Uc为相电压幅值;φ0为a相电压的初相角;ω为角频率。
由6脉动LCC两极直流母线的输出电压波形经傅里叶级数展开可得到3脉动谐波电压源V3p(t)和V3p(t-T/6)(6脉动LCC负极直流母线输出电压的傅里叶级数展开形式的相反数),其中V3p(t)可以表示为
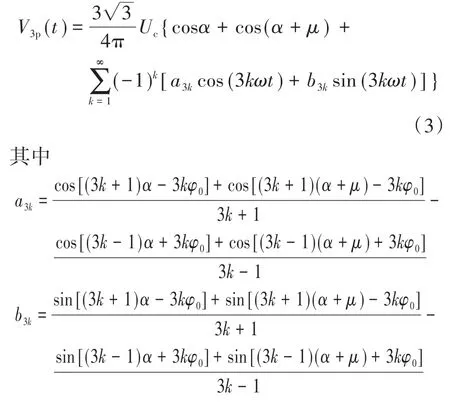
式中:α为触发角。
应该注意到两个等效电压源相位相差60°,这是因为LCC在正常运行时的相邻两次晶闸管换相过程分别发生在上桥臂和下桥臂,且相位间隔为ωt=π/3。
由12脉动LCC换流器的3脉动谐波电压源等值模型可分析各种频次谐波电压、电流的分布有如下特征:12脉动LCC直流侧输出的12k次谐波电压和电流将经直流系统结构传递到VSC侧,也就是说VSC直流侧电压、电流谐波主要为12k次,而电压、电流谐波的进一步定量分析工作还需考虑混联型LCC-VSC系统直流侧其它部分(LCC的直流滤波器、VSC换流器、直流线路等)的等值电路。
2 LCC-HVDC直流滤波器数学模型
由第1节分析可知,12脉动LCC直流侧输出12k次谐波电压和电流,而谐波电压和电流的存在将降低系统的传输容量,增加系统运行损耗,为此一般在LCC直流侧配置滤波器以降低直流系统电流中的12k次谐波分量。
现有的LCC直流滤波器主要为无源式滤波器,通常采用双调谐滤波器或三调谐滤波器,电路结构如图2所示。滤波器电路参数决定了滤波器可滤除的电流频率,一组双调谐滤波器和三调谐滤波器可分别滤除两个和三个不同频率的谐波。对于12脉动换流器,通常釆用两组双调谐滤波器或一组三调谐滤波器,其中,两组双调谐滤波器分别负责滤除12/24和12/36次谐波,一组三调谐滤波器则负责同时滤除12/24/36次谐波[21]。

图2 直流滤波器等值电路Fig.2 DC filter equivalent circuit
3 VSC换流器的直流谐波等效模型
在高压大容量的应用场合,VSC通常采用模块化多电平换流器(multilevel modular converter,MMC),其直流侧谐波含量低,一般无需在直流侧配置滤波器。
VSC直流侧谐波等值电路如图3所示,考虑到VSC换流器三个相单元结构的对称性,混联型LCCVSC系统直流侧的谐波电流i3p_out将在三个相单元中均分,即流过每一相桥臂的电流可以表示为i3p_out/3。因此,对于VSC的一个相单元,有如下表达式:

图3 VSC直流侧谐波等值电路Fig.3 DC side harmonic equivalent circuit of VSC

式中:Cphase为VSC换流器任一相单元的等值电容;u3p_vsc为LCC直流侧谐波经直流系统结构传递到VSC侧的谐波电压。
考虑到任意时刻每个相单元2N个子模块中的N个子模块导通(N为桥臂子模块数),可得到Cphase=2C0/N,C0为每个模块的电容。
对式(4)进行等价变形可得:

从而,VSC直流侧谐波分析模型可由一个大小为Ceq的电容和一个大小为Leq的电感的串联形式的无源元件等值。Ceq和Leq的表达式为

4 受端混联型LCC-VSC直流侧谐波模型
考虑到混联型LCC-VSC系统为真双极系统,正常运行时正、负极保持对称运行,因此针对系统直流侧的谐波计算取正、负极中的任一极分析即可。结合前述直流系统各元件的谐波等效模型,可建立用于分析混联型LCC-VSC系统直流侧谐波的等效模型,如图4所示。其中,下标rec,inv分别表示整流侧和逆变侧LCC。

图4 受端混联型LCC-VSC系统直流侧谐波的等效模型Fig.4 Equivalent DC side harmonics model of receiving end hybrid LCC-VSC
图中,U3p_vsc为VSC直流侧的谐波电压,考虑到LCC的谐波特性,U3p_vsc主要包括12k次谐波分量。对于每一种频率的谐波分量,可分别按照正弦稳态电路的分析方法进行求解。
5 算例
受端混联型LCC-VSC系统拓扑结构采用类似白鹤滩工程拓扑结构,如图5所示,直流输电系统的整流侧采用LCC,而逆变侧则采用高压阀组LCC与低压阀组三端并联VSC相串联的结构,其参数如表1所示。

图5 受端混联型LCC-VSC算例拓扑结构Fig.5 Topology of receiving end hybrid LCC-VSC case

表1 受端混联型LCC-VSC模型参数Tab.1 Parameters of the receiving end hybrid LCC-VSC
以下主要对算例系统直流侧谐波进行仿真验证,主要从谐波频次和谐波幅值两个方面来开展。其中,谐波频次由谐波源(即LCC换流器)的直流侧输出决定,可通过直流场内任一点的电压、电流响应进行验证;谐波幅值的验证包含LCC的等值谐波源验证和VSC谐波响应验证两个部分。
5.1 直流谐波频次验证
考虑到直流谐波频次不受直流场内选取的分析点的影响,取送端LCC正极直流母线电压、电流为分析对象,其频谱分析结果如图6和图7所示。
由图6、图7可知,送端LCC换流器直流侧电压、电流谐波响应主要以12k倍频为主,与前面理论分析结果一致。值得说明的是,图6所示频谱分析结果是计及LCC直流滤波器的滤波作用后得到的,可以看到,在12/24倍频的双调谐直流滤波器作用下,LCC直流侧电压波动将不再以12和24倍频分量为主,取而代之的是频率次低的12k倍频分量(如36,48,60倍频);由图7可知,LCC直流侧电流依然以12倍频分量为主,其次为36,60和72倍频。

图6 送端LCC正极直流电压频谱分析结果Fig.6 Spectrum analysis results of DC voltage of LCC at sending end

图7 送端LCC正极直流电流频谱分析结果Fig.7 Spectrum analysis results of DC current of LCC at sending end
5.2 直流侧谐波幅值验证
根据表1的参数,可建立混联型LCC-VSC系统直流侧谐波的等效模型,如图8所示。其中,VLCC_rec(ω),VLCC_inv(ω)分别表示送端和受端 LCC 的谐波电压源相量,与谐波角频率 ω 有关,udc_MMC(ω)表示对应频率下MMC直流侧电压响应。由前述分析可知,混联型LCC-VSC系统直流谐波频次为12k,以下在各个12k次频率下对送、受端LCC谐波电压源 VLCC_rec(ω),VLCC_inv(ω)以及 MMC直流侧电压响应 udc_MMC(ω)进行仿真验证。

图8 算例直流侧谐波的等效模型Fig.8 Equivalent DC side harmonics model of the case
由式(3)计算 VLCC_rec(ω),VLCC_inv(ω)的理论值,此外通过对实例的仿真可以得到 VLCC_rec(ω)和 VLCC_inv(ω)的真实值,其结果如表2所示。送端LCC谐波源最大误差为1.54%,受端高压阀组LCC谐波源最大误差为8.31%,均不超过10%。对于受端VSC,其直流电压谐波和直流电流谐波误差都比较小,如表3所示,验证了上述理论的正确性和有效性。

表2 LCC谐波电压源的仿真验证Tab.2 Verification of LCC harmonic voltage source

表3 VSC谐波电压源的仿真验证Tab.3 Verification of VSC harmonic voltage source
6 结论
通过研究LCC,VSC和直流滤波器的拓扑结构和变换特性得到LCC,VSC和直流滤波器的直流侧谐波等效模型。在此基础上,考虑受端混联型LCC-VSC系统的拓扑结构和连接方式,提出其直流侧谐波计算等效模型。通过某混合直流输电实例验证所提直流侧谐波计算结果与仿真结果的误差不超过10%,验证了其有效性和准确性。该项目成果可以指导受端混联型LCC-VSC的控制保护技术。

