Gaussian shaper for nuclear pulses based on multilevel cascade convolution

Min Wang · Jian‑Bin Zhou · Xiao‑Ping Ouyang · Ying‑Jie Ma · Xu Hong

Abstract For nuclear measurements, it is necessary to obtain accurate information from nuclear pulses, which should be obtained by first shaping the pulses outputted by the detectors. However, commonly used pulse-shaping algorithms have certain problems.For example, certain pulse-shaping algorithms have long dead-times in high-counting-rate environments or are difficult to achieve in digital systems. Gaussian signals are widely used in analog nuclear instruments owing to their symmetry and completeness. A Gaussian signal is usually implemented by using a multilevel S—K filter in series or in parallel. It is difficult to construct a real-time digital Gaussian filter for the complex Gaussian filtering algorithm. Based on the multilevel cascade convolution, a pulse-shaping algorithm for double exponential signals is proposed in this study, which, in addition to double exponential signals, allows more complex output signal models to be used in the new algorithm. The proposed algorithm can be used in high-counting-rate environments and has been implemented in an FPGA with fewer multipliers than those required in other traditional Gaussian pulse-shaping algorithms. The offiine processing results indicated that the average peak base width of the output-shaped pulses obtained using the proposed algorithm was reduced compared with that obtained using the traditional Gaussian pulse-shaping algorithm. Experimental results also demonstrated that signal-to-noise ratios and energy resolutions were improved, particularly for pulses with a low energy. The energy resolution was improved by 0.1—0.2% while improving the counting rate.

Keywords Impulse shaping · Multilevel cascade convolution · S—K filter · Gaussian-like distribution · Double exponential signal

1 Introduction

Nuclear radiation signals carry information such as the energy of radiation particles, type of radiation particles,and time of radiation events, among other information [1].Basic scientific research regarding nuclear characteristics,nuclear structure, and nuclear decay can benefit from the better understanding of nuclear radiation [2]. However, the nuclear pulse signal produced by the nuclear radiation detectors rapidly increases and exhibits a slow decline, which affects both the peak position of the energy spectrum curve and the resolution of the energy. Therefore, it is essential to process the nuclear signal using electronic techniques before receiving the correct nuclear information from the signal.

Nuclear signal processing technology has been developing for many years. In 1973, Koeman studied digital filters based on the X-ray fluorescence measurement technology[3]. With the development of high-speed ADC and programmable logic circuits, research regarding nuclear signal digital processing technology rapidly developed in the middle and late 1990s. These studies mainly focused on improving the quality of nuclear measurements using digital processing technology. Jordanov et al. performed several studies regarding nuclear pulse processing, such as the digital synthesis of pulse shapes in real time, identification of rise time,and digital pulse-shaping based on weighting factors. These studies have built a theoretical foundation for subsequent researchers globally in the field of nuclear signal digital processing [4]. China began to engage in digital nuclear signal processing relatively late. After 2000, Wuyun and Yixiang of the Tsinghua University and Ruanyu and Qinghua of the Sichuan University began researching digital nuclear signal processing [5]. Subsequently, Jianbin [6] and Guoqiang[7] of the Chengdu University of Technology made certain achievements in the field of nuclear signal processing. These studies provide researchers with basic ideas and a path for further research.

Currently, trapezoidal, cusp, and Gaussian filters are being focused on in the study of nuclear signal digital processing. The sawtooth filter is a supplementary method for pulse shape discrimination (PSD), and impulse response shaping (IRS) is often used in high-countingrate environments. The Gaussian filter has a significant advantage in improving the energy resolution and reducing the effect of the ballistic deficit. The Gaussian filter is a low-pass filter that sufficiently performs in noise suppression, particularly when using high-order derivatives.The Gaussian pulse-shaping method can achieve nearly the best energy resolution in real-time environments [8]and is widely used in traditional high-performance analog nuclear spectrometer systems [9]. However, the true-Gaussian pulse-shaping algorithm is difficult to achieve in an analog system owing to its anti-causality part. Previously, the Gaussian filter was usually achieved by using pseudo-Gaussian [10] or multi-stage S—K filters [11] in nuclear detection systems. In 1973, Puncochar analyzed the application of the S—K filter in an operational amplifier [12]. S—K filters were previously implemented using analog circuits and are the foundation for the study of Gaussian pulse-shaping.

With the development of electronic and computer technologies, digital pulse processing and Gaussian pulseshaping technology for nuclear signals have made significant progress. The progress can be divided into two stages. In the first stage, the nuclear pulses outputted by the detection systems were often simplified as exponentials. In 1995, Young and Vliet proposed a recursive Gaussian pulse-shaping algorithm that is faster than the convolution pulse-shaping algorithm [13]. In 2005, Shiguo et al. proposed a Gaussian pulse-shaping algorithm using wavelet transform [9]. In 2011, Nakhostin et al. proposed a recursive semi-Gaussian pulse-shaping algorithm using a CR-(RC)n circuit [14]. In 2013, Jianbin and Wei established a digital recursive Gaussian pulse-shaping algorithm based on the analog Sallen—Key filter, which achieved a good performance [11]. In 2016, Qing designed a digital Gaussian shaping system based on the transformation of the time—frequency and frequency domains [15]. In the second stage, nuclear pulses outputted by the detection systems were often simplified as a dual-exponential pulse.In 2018, Kantor and Sidorov achieved a digital Gaussian pulse-shaping algorithm using Fourier transform [16]. The Gaussian pulse-shaping algorithm has a better performance considering the improvement of the energy resolution compared with that of the trapezoidal pulse-shaping algorithm in a high-counting-rate environment [17]. However, the Gaussian pulse-shaping algorithm is difficult to implement in DSP and FPGA. Zhangjian of the Chengdu University of Technology constructed and achieved a partial-Gauss pulse-shaping algorithm using third-order derivative operations [18].

Digital pulse processing technology for nuclear signals has gradually matured with the development of high-speed digital processing chips and ADC. Digital energy spectrometers with digital chips have the advantages of high performance and speed for real-time measurements. However, the application of digital algorithms to digital chips encounters a high technical threshold and a long development cycle. Owing to their poor floating-point arithmetic ability, complex algorithms cannot be easily applied to digital chips [19]. The implementation of these algorithms is significantly limited by the availability of digital chips.Algorithms that are suitable for digital chips should avoid floating-point operation and reduce the use of DSP, multipliers, and other resources. The Gaussian pulse-shaping algorithm is complex in terms of the arithmetic operations. However, it is difficult to construct a real-time digital Gaussian filter. Previously, single or double multipliers were often used for signal processing. The speed of the direct convolution algorithm for signals is significantly low,and the real-time convolution algorithm for signals has not gained sufficient attention. With the development of FPGA,systems with dozens of multipliers have appeared, which are fast in parallel convolution computing and are widely used in AI technology.

Based on the previous studies regarding S—K filtering and dual-exponential impulse shaping in digital pulse processing, this study proposes a pulse-shaping algorithm for double exponential signals using multilevel cascade convolutions. Compared with other pulse-shaping algorithms, the proposed algorithm exhibits a better performance and is easy to achieve using digital chips. This new algorithm provides a new means for achieving digital nuclear energy spectrum systems with a high energy resolution in high-counting rate environments.

2 Traditional Gaussian pulse‑shaping algorithm

The raw nuclear signal pulses are biexponentially distributed, causing a loss of energy resolution owing to the amplitude loss, stacked pulses, and noise. In digital nuclear instrumentation, pulse-shaping algorithms are often used to improve the energy resolution and technical rate of a system.In conventional analog nuclear instrumentation systems, filtering is performed using circuit shaping methods, such as the R—C integral, C—R differential, and S—K. There are also many filtering and shaping methods in digital nuclear instrumentation systems.

The Gaussian pulse-shaping algorithm provides a good signal-to-noise ratio and stable amplitude for nuclear pulses.The energy and time information carried by the radiation signals can be accurately obtained using the Gaussian pulseshaping algorithm. The maximum amplitude of the shaped pulse using the Gaussian pulse-shaping algorithm represents the energy of the radiating particles. Previously, the standard for evaluating analog systems using Gaussian pulse-shaping was to compare the approximation between the shaped signal and the standard Gaussian signal. With the development of electronic technology, the output signal model used by Gaussian pulse-shaping has evolved from a single exponential signal to a dual-exponential signal. The pulse-shaping algorithm using single exponential signals usually adopts Gaussian pulse-shaping methods based on an S—K filter or wavelet transform [20].

2.1 Semi‑Gaussian pulse‑shaping for single exponential signals

A semi-Gaussian pulse-shaping method for single exponential signals was developed using S—K filters. The S—K filter[11] is described as follows:

wherekandadenote the parameters of frequency and amplitude, respectively.

Fig. 1 Block diagram of semi-Gaussian pulse-shaping using S—K transform

For Fig. 1, considering the input signal of the S—K system isx[n] and the output of the S—K system isy[n], Eq. (1) can be described by Eq. (2) as follows:

The input and output signals of the S—K system are shown in Fig. 2. The resulting purple curve of the synthesized signal plot approximates as a Gaussian distribution.

Another semi-Gaussian pulse-shaping method for single exponential signals was constructed using wavelet transform[9]. Considering the input signal asx[n] and the output signal asG[n], the pulse-shaping algorithm can be described as follows:

whereg[n] is the signal model for the Gaussian function,AandBare the amplitudes of the pulses,his the full width at half maximum (FWHM) of the pulses,bis the offset, andτis the time-decay constant. Equation (10) demonstrates that the Gaussian pulse-shaping algorithm is a linear combination of these two parts. The first part is the convolution of a single exponential signal and a Gaussian function. The second part is the convolution of a single exponential signal and a first-order derivative of the Gaussian function.

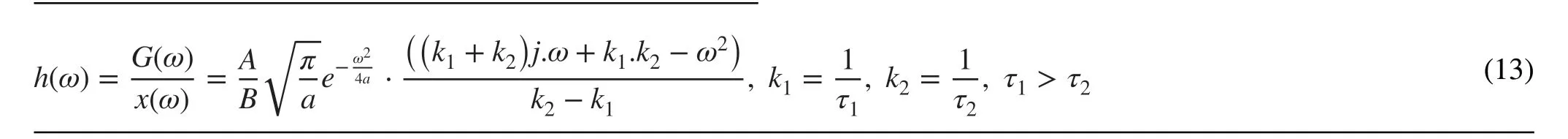
The input signals for the two aforementioned algorithms were simplified to single exponential signals. However, signals outputted by detector systems are closer to dual-exponential or exponential signals, with more time constants.Algorithms based on complex exponential signals are difficult to achieve in DSP or FPGA. The algorithm is complex and requires too many multipliers to build the parallel systems, which consumes significant hardware resources of the digital chips.in Eq. (12) [17]. The output signals of the algorithm are standard Gaussian signals, which can be described using Eq. (11). The response function in the frequency domain,which is described in Eq. (13), can be derived using Eq. (12).In Eq. (13),h[n] is obtained using a discrete fast Fourier transform. A digital Gaussian pulse-shaping algorithm can be achieved by convoluting the measured signals with h[n].The disadvantage of the algorithm is thath[n] is significantly long and an extensive amount of multipliers are used to achieve the algorithm. The parameters of the algorithm are difficult to modify once they are set. In this study, a Gaussian pulse-shaping algorithm based on the multilevel cascade convolution (MCC) is constructed.

2.2 Gaussian pulse‑shaping for dual‑exponential signals

With the improvement of the ADC sampling rate in digital systems, the reduction in noise in the detector amplification system, and the improvement of sampling accuracy, the rising edge of the nuclear pulse can be described accurately.Previous studies have indicated that the output pulses of detection systems should be approximated as dual-exponential signals, as described in Eq. (12). An algorithm proposed by Kantor is based on the dual-exponential signals described

Fig. 2 (Color online) Simulations of the input and output signals in the S—K system

Figure 2 demonstrates that the Gaussian pulse is symmetrical and the weighting effect first increases and then decreases, with a maximum value at the relative center. The distribution parameter in Eq. (12) determines the width of the function image. The distribution parameter is inversely related to the smoothness. A change in the distribution parameters does not change the number of extreme values of the Gaussian function; there is only one extreme value.The optimized Gaussian function has the minimum product of the time and frequency widths. The value of σ determines the width of the Gaussian curve, as shown in Fig. 2. Different filtering requirements for nuclear signals can be satisfied by adjustingσ.

3 MCC Gaussian pulse‑shaping algorithm

3.1 IRS algorithm for dual‑exponential signals

Fig. 3 IRS based on the multilevel cascade convolution

Fast pulse-shaping methods have been rapidly developed in recent years to obtain the counting rate and event time of nuclear signals. Fast pulse-shaping methods include the narrow triangle pulse-shaping and IRS methods for dualexponential signals [21]. However, nuclear signals accumulate in a high-counting-rate environment, which significantly reduces the counting accuracy of nuclear signals. Existing solutions include reducing the width of nuclear pulses [22],extrapolation based on the reference waveform [23], maximum likelihood estimation [24], deconvolution [25], and IRS for dual-exponential signals [26]. The pulses outputted by these methods are relatively wide and the dead time of the nuclear signals due to pile-up remains relatively large, which makes it impossible to accurately count in a high-countingrate environment. The dead time of the fast signal obtained using the method described above remains relatively large.Building a fast pulse-shaping method is required for reducing the dead time and improving the counting rate and accuracy of the event time of the nuclear signal. To obtain accurate nuclear signal information, a pulse-shaping algorithm can be achieved in the FPGA. To reduce the width of the output pulse, a dual-exponential signal model is adopted in the new algorithm, which must consider the rise time of the nuclear pulses, ballistic effect, and energy resolution upon implementation.

In this study, a dual-exponential function was adopted as the output signal model. Before Gaussian pulse-shaping,nuclear signals are first shaped into unit impulses. The process of shaping the dual-exponential pulses into unit impulses is illustrated in Fig. 3, where INV_RC indicates an inverse RC circuit. The digital solution for INV_RC was established in a previous study [27].

The new IRS algorithm was implemented using two INV_RC circuits, as shown in Fig. 3. The dual-exponential pulses are shaped into single exponential pulses by the first INV_RC. Single exponential pulses were shaped into unit impulses by the second INV_RC. Previous studies have shown that unit impulses can be shaped into single exponential pulses using an RC circuit [28]. The amplitude of the single exponential pulse is reduced to 1/Mof the original unit impulse. Therefore, the amplitude of the unit impulse obtained using the proposed IRS algorithm must be reduced by 1/M.

The system function in the S-domain of an RC system is described using Eq. (14). The system function in the time domain of the RC system, which is described using Eq. (15),can be derived from Eq. (14) using the inverse Laplace transform. The convolution of the unit impulse and Eq. (15)is a negative exponential signal. The unit impulse can be obtained by deconvolution of the negative exponential signal and RC system function. The deconvolution function of the RC system is expressed using Eq. (16).

In Fig. 3, the input signal of the first INV_RC isx[n], as described in Eq. (17), the output signal of the first INV_RC isy[n], as expressed in Eq. (18), and the output signal of the second INV_RC isp[n], as expressed in Eq. (19).

In Eqs. (17), (18), and (19),mandMare the system parameters.

Equations (20) and (21) can be derived from Eqs. (18)and (19) by using a digital solution of the INV_RC system.

Equations (23), (24), and (25) can be derived from Eq. (22) using the difference operations.

Equation (25) is the digital solution of the IRS algorithm for the dual-exponential signals. The digital solution was derived based on a multilevel cascade convolution.

Equation (24) can be written as Eq. (26), and the impulse response of the system is described using Eq. (27). Equation (28) is the convolution function of the system for single exponential signals.

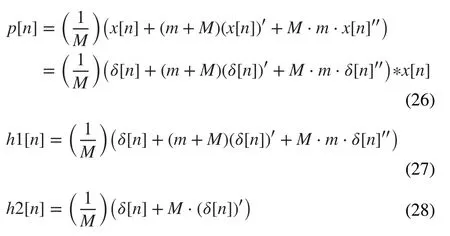
3.2 MCC standard Gaussian pulse‑shaping algorithm

The method used in this study is different from the multilevel cascade deconvolution used in a previous study [29].The convolution between the standard Gaussian signal and impulses obtained using Eq. (27) was studied. Standard Gaussian signals can be obtained using Eq. (29). The dualexponential signals outputted by the detector and impulses shaped using the new algorithm are displayed in Fig. 4a. The impulse, standard Gaussian, and digital Gaussian shaping signals are shown in Fig. 4b. As shown in Fig. 4, the new method achieves digital Gaussian pulse-shaping for nuclear signals.

Equations (30), (31), and (32) can be derived from Eqs.(27), (27), (28), and (29). Equation (30) provides a digital solution for the convolution between the standard Gaussian signal and impulses obtained from single exponential signals. Equation (31) provides a digital solution for dualexponential signals. Equation (32) provides a digital solution for dual-exponential signals with undershoots. Figure 5 displays the experiment result of Eq. (31).

Fig. 4 (Color online) a IRS for dual-exponential signals outputted by SDD; b Simulation of Gaussian pulse-shaping for SDD impulses

Fig. 5 Convolution between Gaussian and dual-exponential signals. a Gaussian signal with short rise time; b Gaussian signal with long rise time

Fig. 6 (Color online) Simulation of MCC standard Gaussian pulseshaping for SDD signals

Consideringx[n] as the input signal, impulses can be obtained using the convolution ofx[n] andh1[n], as described in Eq. (27). The impulses are then convoluted with a standard Gaussian signalg[n] to obtain a Gaussian output signal. This is the Gaussian shaping process for dual-exponential signals, as described in Eq. (33). The convolution sequence for the signals can be exchanged according to the commutative property of a convolution. Letx[n]convolute with the Gaussian signalg[n] first, and then withh1[n], as described by Eq. (34). Figure 6 presents a simulation of the convolution between the SDD and Gaussian signals described in Fig. 5. The shaped pulses are shown in Fig. 6, denoted by red dotted lines. The MCC standard Gaussian pulse-shaping algorithm can be implemented using either Eqs. (31) and (33) or Eqs. (18) and (27).

3.3 Construction of a MCC algorithm with step and Gaussian first derivative

Subtraction may result in negative numbers and produce truncation errors in digital chips. To improve the performance of the digital system, additions rather than subtractions were chosen in the algorithm implemented in the digital chips. Subtractions exist in the IRS algorithm. To achieve the IRS algorithm, a digital system requires numerous hardware resources. Therefore, the IRS algorithm cannot be implemented in commonly used medium- and low-end digital systems. To avoid subtraction, continuous step signals are adopted in the implementation of the new pulseshaping algorithm. The continuous step signal, which has a random amplitude and step hold time, is the output signal of the switch-reset type charge-sensitive amplifier. Continuous step signals can be achieved using addition in digital systems, which is more suitable.

Gaussian first-order derivatives are used because if a Gaussian signal is directly convoluted with a step signal,the output signal will have a long tail, which will cause accumulation and affect the counting rate of the nuclear signals.Based on the aforementioned factors, the first derivative of a Gaussian signal was finally selected to convolute with the step signal. In the simulation of the algorithm, the input signal adopts a continuous step signal and the first derivative of the Gaussian signal. The continuous step signal and first derivative of the Gaussian signal are denoted by black and red dotted lines, respectively, in Fig. 7a. The simulation of the output signal is shown in Fig. 7b. Figure 7 demonstratesthat continuous step signals and the first derivatives of the Gaussian signals can be chosen as the input signal of the new pulse-shaping algorithm. The coefficient of the digital Gaussian convolution can be determined using Eq. (35), as follows:

whereHis the FWHM of the Gaussian distribution.

3.4 Extension of the MCC Gaussian pulse‑shaping algorithm

Digital Gaussian pulse-shaping is used to build a multilevel cascade convolution algorithm, which outputs Gaussian pulses using a convolution between the Gaussian and nuclear signals.

In addition to the Gaussian signals, other signals were tested in the MCC pulse-shaping algorithm. An MCC pulse-shaping algorithm was developed for the target signal.Nuclear signals convolute with the target signal. The output and target signals were compared to evaluate the similarity between these signals.

Trapezoidal signals were tested; the MCC trapezoidal pulse-shaping for single exponential signals and dual-exponential signals is shown in Fig. 8a, b, respectively. Figure 8a presents a partial simulation of the pulse-shaping effect when the time constant of the input signal is equal to the rise time of the trapezoidal pulse. The result of shaping single exponential signals into impulses and then convoluting them with the trapezoidal signal is presented. Figure 8a demonstrates that MCC trapezoidal pulse-shaping is suitable for single exponential signals. The dual-exponential signals can be used in the MCC trapezoidal pulse-shaping algorithm, as shown in Fig. 8b.

Cosine and Cauchy signals were tested using the MCC pulse-shaping algorithm. The experimental results are shown in Fig. 9. First, the convolution signal in Fig. 7 was replaced with the cosine squared first-order derivative signal,for which the simulation results are shown in Fig. 9a; the bottom of the shaped signal converges faster and the top is smoother. The coefficient of the digital cosine square convolution can be determined using Eq. (36), where H is the FWHM of the COS square distribution [30].

In other experiments, the convolution signal was replaced with the first derivative of the Cauchy signal. The Cauchy distribution has the advantages of a sharp top, simple mathematical model, and easy separation of overlapping pulses.The convolution signal in Fig. 7 was replaced with the first derivative of the Cauchy signal, and the simulation results are shown in Fig. 9b; the top of the shaped signal is sharp,and the tail of the pulse is evident. The coefficient of the digital Cauchy convolution can be determined using Eq. (37),whereHis the FWHM of the Cauchy distribution.

Fig. 8 Simulation of convolution signals outputted using the trapezoidal pulse-shaping algorithm. a Trapezoidal pulse-shaping for single exponential signals; b Trapezoidal pulse-shaping for dual-exponential signals

The aforementioned signals demonstrate that the algorithm has a strong universality. The MCC pulse-shaping algorithm, which is built using the target signal, can be optimized by parameter selection.

4 Experimental results and analysis

The experimental results for the ideal signals demonstrate that the digital MCC pulse-shaping algorithm displays good characteristics in the frequency domain. The digital MCC pulse-shaping algorithm was tested using real signals output by the detectors. The digital MCC Gaussian pulse-shaping algorithm is complex in arithmetic operations, which require certain FPGA resources. The digital signal processing system, which was implemented in FPGA (Xilinx ZYNQ7020),can provide more than 220 DSP units. In the digital system,68 DSP units were used for digital Gaussian pulse-shaping, 65 DSP units were used for Gaussian convolution, and three DSP units were used for IRS for the dual-exponential signals. The digital signal processing system used for the energy spectrum measurements is shown in Fig. 10. To ensure the accuracy and speed of the calculation, the negative number operation was removed, and all floating-point calculations were converted into 64-bit positive integer calculations, which avoids truncation errors and ensures the overall performance of the algorithm.

A digital nuclear detection system was built to test the MCC Gaussian pulse-shaping algorithm. An NaI(Tl)detector (Φ75 mm × 100 mm) was used in the system. The algorithm was implemented in FPGA. The signal’s output by the NaI(Tl) detector was shaped using the MCC Gaussian pulse-shaping algorithm. The shaped signals exhibit good symmetry, a high approximation with the Gaussian signals,and low noise, as shown in Fig. 11a. The shaped digital pulse obtained using the proposed algorithm had 65 sampling points. The FWHM of the shaped pulse obtained using the new algorithm had 16 points, which is approximately 1.65 μs. The FWHM of the shaped pulse obtained using the traditional algorithm was approximately 3—4 μs, and Cs-137 was tested using the digital nuclear detection system. The energy spectrum obtained using the new algorithm is shown in Fig. 11b. The FWHM of the characteristic peak in Fig. 11b was 6.81%. The FWHM of the characteristic peak obtained using the traditional algorithm was 7.0%. The energy resolution was improved by approximately 0.1—0.2%.Compared to the energy spectrum of the previous test system, the low-energy part in Fig. 11b is more apparent. This demonstrates that the new algorithm has advantages in terms of pulse separation and noise suppression. The composite energy spectra of Cs-137, K-40, and Th-232, whose characteristic peaks were identified and linear correlations were analyzed, are shown in Fig. 11c. TheR-squared value (COD)of the characteristic peaks was 0.999991. The experimental results show that the energy spectrum obtained using the proposed algorithm is linear.

Fig. 9 a Simulation of convolution between continuous step signals and first-order derivatives of cosine squared signals (H = 128 samples). b Simulation of convolution between continuous step signals and first-order derivatives of Cauchy signals

Fig. 10 (Color online) Digital signal processing system for energy spectrum measurement (ZYNQ)

Fig. 11 Experiment results of energy spectrum. a Gaussian pulseshaping result of real signals; b Energy spectrum of Cs-137; c Composite energy spectrum of Cs-137, K-40, and Th-232

5 Conclusion

In this study, several traditional digital Gaussian pulseshaping algorithms were investigated and tested. Based on traditional algorithms, a digital MCC Gaussian pulseshaping algorithm was developed and implemented in an FPGA. First, the impulsive forming of double exponential signals using a digital Gaussian convolution algorithm was established. The nuclear signals were shaped using the IRS algorithm. The output signals were then shaped using the MCC Gaussian pulse-shaping algorithm. The convolution sequence for the signals can be exchanged according to the commutative property of the convolution. Nuclear signals can first convolute with the Gaussian signal, followed by dual-exponential signals using the IRS algorithm. Second,the step signal and digital Gauss convolutional forming algorithm model were constructed, and the step signal output from the detector was cascaded with Gaussian convolution to obtain the mathematical model of the multi-stage cascaded digital Gaussian convolutional forming algorithm.The experimental results demonstrate that the pulse-shaping algorithm removes the tail of the pulse, improves its symmetry, and narrows the pulse width, which is suitable for energy spectrum measurements in a high-counting-rate environment. In the experiment, the algorithm was expanded to include trapezoidal, cosine, and Cauchy signals. The experimental results show that the pulse-shaping algorithm proposed in this study is suitable for these signals and can be optimized by parameter selection.

In this study, a digital Gaussian pulse-shaping system was implemented. Compared with analog Gaussian pulseshaping systems, the new system has an improved energy resolution and is more convenient for adjusting the shaping parameters for real signals. Compared with digital S—K filters, shaped pulses outputted by the new system remove the tail, which makes their symmetry better and width narrower.This new digital system is more suitable for energy spectrum measurements in high-counting-rate environments. Compared with the digital Gaussian shaping algorithm based on wavelet transform, the multiplier in the new system is reduced. The new algorithm can be used for signals such as dual- and triple-exponential signals. Compared to a system based on a discrete Fourier transform, the complexity of the new system is reduced, and the shaping parameters are more convenient for real-time adjustment. Compared with other pulse-shaping methods, the MCC shaping method has a wide applicability and can optimize the characteristics of the target signal by parameter adjustment.

Experimental results show that the real-time digital Gaussian forming system based on the MCC algorithm is significantly simpler than the previous algorithm system,which can run in parallel with the AD sampling system at a high speed.

Scintillation detectors can be deployed on medium- and low-end FPGA devices with more than a dozen of multipliers. Semiconductor detectors with a high resolution must be deployed with more than hundreds of multipliers or medium- and high-end FPGA devices of the DSP.An NaI(Tl) detector (Φ75 mm × 100 mm) was used in the digital nuclear detection system. The signals output by the detectors were shaped using the new algorithm. The FWHM of the shaped pulse obtained using the new algorithm was approximately 1.65 μs and that obtained using the traditional algorithm was approximately 3—4 μs. The results demonstrate that the width of the shaped pulse becomes narrower,which is more suitable for energy spectrum measurements in a high-counting-rate environment. The FWHM of the characteristic peak obtained using the new algorithm was 6.81%,whereas that obtained using the traditional algorithm was 7.0%. The energy resolution was improved by approximately 0.1—0.2%. The low-energy part of the energy spectrum for Cs-137 obtained using the new algorithm was more apparent. This demonstrates that the new algorithm has advantages in terms of pulse separation and noise suppression.Composite energy spectra for Cs-137, K-40, and Th-232 were obtained using the new algorithm. TheR-squared value (COD) of the characteristic peaks was 0.999991. The experimental results demonstrate that the energy spectrum obtained using the proposed algorithm is linear. The MCC Gaussian pulse-shaping algorithm designed in this study offers significant advantages for digital detection systems.

Author contributionsAll authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Min Wang, Jian-Bin Zhou and Ying-Jie Ma. The first draft of the manuscript was written by Min Wang and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.