灵活检修工艺下地铁车辆架大修作业调度优化方法

陈绍宽，王丹阳，刘致远，刘葛辉，冯佳,1b

(1.北京交通大学，a.交通运输部综合交通运输大数据应用技术交通运输行业重点实验室，b.中国综合交通研究中心，北京 100044；2.天津市英贝特航天科技有限公司，天津 300141)

0 引言

近20 年来，我国城市轨道交通处于快速发展阶段，运营里程和客流量快速增长。据中国城市轨道交通协会统计，截至2021年底，全国累计配属列车9658 列[1]。按地铁设计规范(GB50157-2013)规定的修程粗略计算，平均每年需要进行架大修作业的列车数量可达1900列以上。随着地铁运营网络规模持续增大，列车配属数量及其运用强度的增加，导致车辆检修工作量的大幅度提升，对保障列车的高可用度和实现企业降本增效提出了挑战。地铁车辆检修作业通常按照既定的修程修制开展，其中，架大修作业具有扣停时间长和作业组织复杂等特点。如何提升车辆架大修作业效率并缩短作业周期，提高列车可用度，具有重要的理论研究与工程实践价值。

既有研究主要从架大修工艺设计展开，其规定了作业处理流程，是作业调度方案制定的重要依据。随着架大修作业规模增大，移位作业工艺相比传统定位作业工艺可有效提高作业效率。移位作业属于流水线作业，通过探究各检修线之间作业能力的匹配关系提升整体作业效率[2]。此外，通过优化调度方案也可提升架大修作业效率。文献[3]针对城市轨道交通线路设施制定长期维修调度方案，以实现降本增效。实际中，结合移位作业工艺的架大修调度问题可视为柔性作业车间调度问题(Flexible Job-shop Scheduling Problem,FJSP)[4]。

FJSP 的研究广泛存在于材料加工、设备制造、流水线装配及大型系统维修等实际场景[5]。在设备维修方面，当维修工艺要求设备按照一定规则通过具有不同作业时间和作业范围的若干维修设备时，维修环境可视为FJSP 问题。例如，文献[6]建立了多约束机器的4S 自动维护车间调度模型；文献[7]以维修人员为研究对象，基于FJSP 制定用于飞机维护的固定工作时刻表。FJSP 通常以最小化完工时间为目标，实际生产流程中还需考虑不同目标，例如，机器工作时间、机器能耗[8]及鲁棒性[9]等。FJSP 的主要约束是工序间的优先级，目前研究集中于单部件(任务)系统，工艺路线为顺序形式[10]；而对于多部件(任务)系统，还应考虑不同部件(任务)间的优先级。文献[11]提出了同时考虑加工与装配任务的FJSP 模型，通过增加两种任务间顺序的优先约束，确保装配任务等待对应零件完成加工任务。此外，部分研究考虑机器间的路径问题，通过分析运输和加工阶段之间的耦合关系，建立有限运输条件下的FJSP模型[12]。

本文建立基于FJSP的车辆架大修作业调度优化模型，旨在自动生成库内检修时间最短的架大修作业调度方案；改进并应用灵活检修工艺作为调度方案的指导工艺，减少作业活动间的非必要次序约束，扩大调度方案的优化范围，达到降低库内检修时间的效果。通过案例对比研究不同检修工艺和多列车等多种场景下生成的架大修作业调度方案的优化效果，验证模型与算法的正确性和有效性，说明灵活检修工艺相比于传统工艺的优越性。

1 问题描述

FJSP 模型是建立地铁车辆架大修作业调度优化模型的基础，该模型主要包括两个子问题：①设备选择，为每项作业活动在一组备选的作业设备中确定一台作为执行对象；②活动排序，对每台设备上作业活动的执行或处理过程进行排序。依据FJSP 模型构建思路，需要明确架大修的作业结构和作业活动间的次序关系和检修资源状况。

(1)作业结构

车辆架大修作业可分解成“项目-子项目-作业活动”三级结构。其中，“项目”指列车的架大修作业；“子项目”指架大修作业的单元，包括整列作业和解编后各类型车辆的检修作业；“作业活动”是最小的作业单元，代表“子项目”中的具体维修任务。

(2)次序关系

作业活动间的次序关系分为并行、顺序和耦合这3种。并行关系表示两个作业活动可同时进行；顺序关系表示同一子项目中作业活动间的先后次序关系；不同子项目间存在次序关系会使所包含的作业活动间形成次序关系，即为耦合关系。上述次序关系具有传递性，当邻接作业活动满足次序约束时，所有作业活动即可保证次序约束。并行关系不产生约束，只需所有存在邻接顺序关系或邻接耦合关系的作业活动满足次序约束即可。6节编组B型列车大修项目的部分作业分解结构如表1所示，其中“邻接前序作业活动”列描述邻接作业活动间的次序关系，“i{j} ”为作业活动集合，i为子项目编号，j为子项目中的作业活动编号，以“、”连接表示作业活动集合的并列。

如表1 所列，子项目1 中“编组”和“静调”为邻接顺序关系，“静调”在“编组”后进行；子项目1 中的“解编”和子项目2 中的“转向架与车体分离”为邻接耦合关系，解编后才允许进行车辆作业。

表1 列车大修项目在灵活作业工艺下的部分工作分解结构表Table 1 Partial work breakdown structure of overhaul repair projects on trains under flexible operation craft

次序关系取决于检修工艺，后者包括检修策略和作业流程两部分。检修策略决定了各车辆进入检修线的顺序，常见的检修策略包括整体同步和阶梯式两种：整体同步是列车编组内所有车辆同步作业，阶梯式是列车编组内各车辆按编组顺序依次进入检修线作业。作业流程规定了列车/车辆进入各检修线进行对应类别作业活动的顺序；固定作业流程最为常见，其主线为串行结构，一般仅允许主线作业活动(车体检修)与支线作业活动(部件检修)并行，作业效率较低。

本文采用灵活检修工艺，包括灵活检修策略和灵活作业流程。灵活检修策略规定各车辆在完成当前检修线的作业后即可进入下一检修线进行作业，不必按照编组顺序，也不必等待其余车辆；灵活作业流程中主线设计采取多工序可并行的串并混合工艺设计，所有并行作业的工序可视情况进行调度调整，以提高架大修作业效率。

(3)检修资源

检修资源包括检修设备和检修人员，两者根据同类型检修作业的需要组合搭配形成检修组。检修组是作业活动最小的直接执行单元，根据需求每类设置若干组，对应的作业活动可从多个可执行的检修组中选取一个，作业活动与检修资源间为柔性关系。

2 架大修作业调度优化模型

本文结合车辆架大修作业项目的三级结构，以FJSP 模型为基础构建架大修作业调度优化模型，在满足次序约束和生产资源约束等的条件下，解决各项作业活动的执行对象(检修组)作业关联问题，优化检修组执行各项作业活动的顺序和时间。

2.1 模型假设

本文研究的假设条件包括：

(1)作业活动不可拆解且须由一个检修组持续执行至结束。

(2)作业时间定义为历史数据规定的任务完成时间，不可缩短或延长。开始前的准备时间和完成后的交付时间计入作业时间内。

(3)不考虑作业活动完成时间延后的情况。

(4)检修组人员和设备资源均满足执行作业活动的要求。

(5)检修组一次只能执行一项作业活动。

(6)在满足工艺约束条件下，所有作业活动之间无额外作业冲突。

(7)车辆在检修线间的转移活动归入到移入检修线的首个作业活动中。

2.2 符号定义

本文对模型中主要参数、集合和变量定义如下：q和p为列车架大修项目编号，q,p=1,2,…,n1，n1为项目数；i和h为子项目编号，i,h=1,2,…,n2,q，n2,q为项目q中子项目的数量；j和l为作业活动编号，j,l=1,2,…,n3,qi，n3,qi为项目q子项目i中包含的作业活动数量。Fq、Pqi及Oqij分别为第q个项目、项目q第i个子项目及项目q子项目i中第j个作业活动，Fq∈F，Oqij∈O，Pqi∈P，F、P及O为对应集合。

m为检修组编号，m=1,2,…,N，N为检修组数量；Mqij为所有可执行作业活动Oqij的检修组编号集合，Mqij⊂M，M为检修组编号集合。

R为邻接作业活动对集合，R=R(b)∪R(u)，R(b)和R(u)分别为邻接顺序关系作业活动对集合和邻接耦合关系作业活动对集合。R(u)=R(u′)∪R(u″)，R(u′)为由整车作业活动和车辆作业活动组成的邻接耦合关系作业活动对集合，R(u″)为由包含了检修线间转移活动的作业活动组成的邻接耦合关系作业活动对集合。

Eq和Zq分别为项目q的入库和库内作业完成时间。sqij和eqij分别为作业活动Oqij的开始和完成时间。Tqijm为由检修组m执行检修作业活动Oqij所需的作业时间。B为一个极大的正数。

xqijm∈{ }0,1 为决策变量，当且仅当作业活动Oqij由检修组m执行时为1；∈{0 ,1} 为决策变量，当且仅当作业活动Oqij和Ophl均由检修组m执行，且Oqij早于Ophl执行时为1。

2.3 模型构建

构建优化模型为

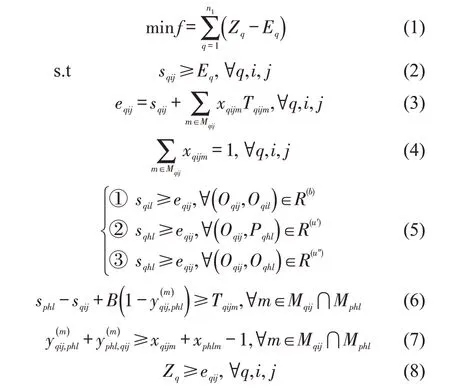
式(1)为目标函数，表示所有列车架大修项目的库内检修作业时间最小，其中，库内检修作业时间为检修作业完成时间与列车入库时间的间隔。式(2)为作业活动开始时间约束，保证项目中所有作业活动开始时间均不早于项目开始时间(列车入库时间)。式(3)为作业活动完成时间约束。式(4)为检修组选择约束，保证每个作业活动都只能由对应的备选检修组集合中的一个执行。式(5)为工艺次序约束，表示所有具有邻接顺序关系和邻接耦合关系的作业活动对需满足作业时间的先后次序约束。①表示邻接顺序约束，Oqij和Oqil存在于同一子项目Pqi中，描述整车作业和车辆作业过程的处理顺序；②表示邻接耦合约束，针对整列作业与车辆作业间的次序关系，整列作业活动Oqij为车辆作业子项目Pqh的耦合关系，则Pqh中作业顺序最前(或最后)的作业活动Oqhl与Oqij为邻接耦合关系，作业时间需要满足次序约束；③表示邻接耦合约束，针对各车辆进入检修线的次序关系，当包含检修线间转移的作业活动Oqij与Oqhl存在邻接耦合关系时，表示车辆作业Pqi和Pqh依次进入对应检修线。式(6)保证由同一检修组执行的作业活动中，后执行作业活动开始时间晚于先执行作业活动结束时间。式(7)保证只有在两个作业活动选择同一个检修组执行时，才存在由同一检修组执行的先后顺序关系。式(8)为列车架大修项目库内作业完成时间的约束。

3 算法设计

本文建立的优化模型属于NP-hard 问题，设计相应的遗传算法求解，采用集成设计算法同时求解检修组选择和作业活动排序两个子问题。针对集成设计算法局部搜索能力较差的问题，通过改进部分算子增强其局部搜索能力的同时避免过早收敛，提高算法的求解效率和稳定性。

3.1 编码机制设计

染色体采用分段编码的形式，分为检修组选择(MS)和作业活动排序(HS)两部分，分别记录检修组编号m和作业活动的实数编码vqij，如图1 所示。为便于进行数字编码，将原作业活动索引形式由“项目序号-子项目序号-作业活动序号”转化为“子项目序号-作业活动序号”，即由(q,i,j) 转化为[(n2,q-1)·q+i,j] ，将子项目以单个架大修项目中子项目的数量n2,q为周期统一排序。

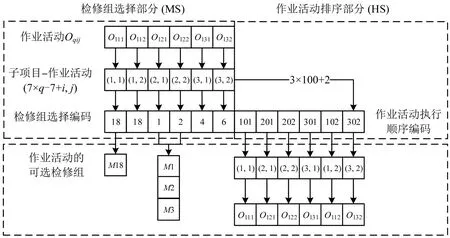
图1 车辆架大修作业调度优化算法编码机制Fig.1 Encoding mechanism of scheduling optimization algorithm

染色体MS 部分的基因位顺序表示作业活动Oqij的次序，作业活动Oqij需要在可选检修组集合Mqij中选择任一检修组m来执行，基因位置上写入m。

染色体HS部分的基因位记录每个作业活动对应的顺序。作业活动编号进行实数转码的公式为：vqij=φ[() ·q+i]+j，vqij为Oqij对应的实数码，φ为放大系数，视子项目的作业活动数量而调整，须保证每个实数码对应唯一的作业活动。例如图1中放大系数为100时，作业活动O132可转码为302。

3.2 解码机制设计

解码过程将染色体编码还原为实际的调度方案，其中，解码MS部分生成执行作业活动Oqij的检修组。解码HS 部分按照实数码顺序，生成作业活动Oqij的开始时间sqij和结束时间eqij。为提高算法效率，使生成的sqij和eqij满足工艺次序约束以及各检修组的作业活动处理顺序约束，设计解码过程如下。

依次读取HS部分未确定作业开始时间的首位基因vqij，转成对应的作业活动Oqij；判断Oqij选择的检修组m是否已经安排除Oqij以外的作业活动，若否，计算Oqij的所有邻接前序作业活动的最迟结束时间(若无邻接前序作业活动，则取项目q开始时间，即=Eq)，sqij=，eqij=+Tqijm；若是，查找检修组m上时间长度大于作业时长Tqijm的空闲时段La(a=1,2,…) ，视为可插空时段，依次判断插空条件max{}+Tqijm≤是否满足(和为时段La开始和结束时间)，若插空条件成立，sqij=max{}，eqij=max{}+Tqijm；若可插空时段均不满足，则Oqij为检修组m当前执行的最后一个检修活动，查找检修组m之前执行的最后一个作业活动的结束时间，sqij=max{}，eqij=max{}+Tqijm。

3.3 交叉、变异及修复算子设计

染色体的MS部分采用均匀交叉，HS部分采用POX(Precedence Operation Crossover)交叉。染色体MS部分采用普通的随机变异操作，HS部分采用随机选择嵌入操作和交换操作两种变异方式。在经过交叉和变异操作后，染色体HS 部分实数码的顺序可能会出现违反次序约束的情况，致使后续无法通过解码生成可行方案，因此，需要执行如下的修复流程。

(1)依次读取染色体HS 部分中尚未进行调整的首位基因vqij，转成对应的作业活动Oqij。判断Oqij的邻接前序活动是否均已经做调整，若否，将基因vqij从染色体HS中剔除，并移至待调整作业活动链表尾部；若是，则保留基因vqij的位置，并将vqij标记为已调整。

(2)依次检验待调整作业活动链表中的基因vqij所对应的作业活动Oqij的邻接前序活动是否均已经做调整，若是，将其在待调整作业活动链表中剔除，并添加在染色体HS 部分上已完成调整的基因之后，并将vqij标记为已调整，重复执行直至待调整作业活动链表中不再有任何基因满足调整条件。循环执行上述2 个步骤，直至染色体HS 部分基因调整完毕。

4 案例研究

4.1 案例背景

以国内某城市地铁线路列车的架大修计划为对象进行案例研究。列车为6节编组B型车，其作业分解结构如表1 所列。单列大修项目包括子项目7个(整列作业1个，带司机室拖车检修2个，带受电弓动车检修2个，动车检修2个)，作业活动347项(整列作业包含5项，带司机室拖车检修包含63项，带受电弓动车检修包含55 项，动车检修包含53项)；单列架修项目相比大修项目少了车体深度维修与喷漆等部分作业活动，包含子项目7个(同大修项目)，作业活动287 项(整列作业包含5 项，带司机室拖车检修包含53 项，带受电弓动车检修包含45项，动车检修包含43项)；“邻接前序作业活动”由检修工艺决定，案例中涉及4 种检修工艺，分别对应架修、大修项目作业分解结构各4 种；“检修组”是每项作业活动对应的执行检修组。检修组的配置数量与编号如表2 所示，与作业分解结构中“检修组”对应，可生成每项作业活动的备选检修组集合。

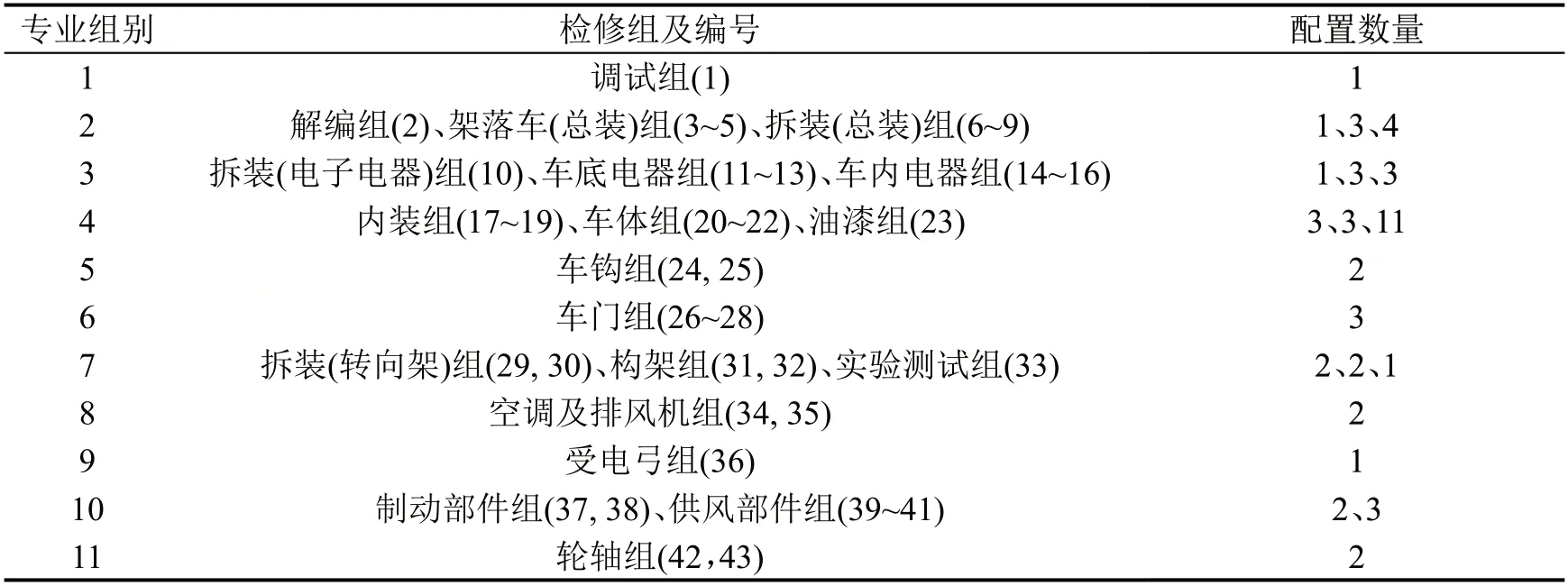
表2 架大修车辆段检修组配置情况Table 2 Maintenance teams in depot for unwheeling and overhaul repairs

输入参数包括：列车架大修在不同检修工艺下的工作分解结构、车辆段检修组配置及遗传算法设计参数等。其中，遗传算法种群包括200 个个体，收敛判断代数为100 代，交叉和变异概率均为0.5，HS部分的两种变异方式选择概率均为0.5。

4.2 单列架大修作业调度优化

应用本文模型和算法分别求解不同工艺下的架修和大修调度方案，其中，灵活工艺下的架修和大修调度方案分别如图2 和图3 所示。在43 个检修组的作业下，单列架修的库内作业时长为217 h，单列大修为297 h。

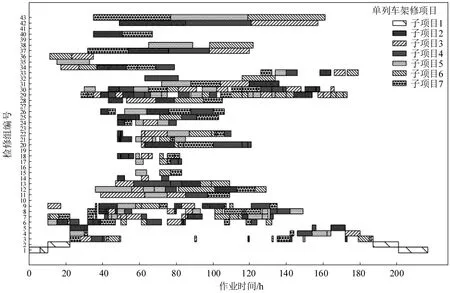
图2 灵活工艺下的单列车架修作业调度优化方案Fig.2 Optimum unwheeling repair schedule for a single-train operation using flexible process

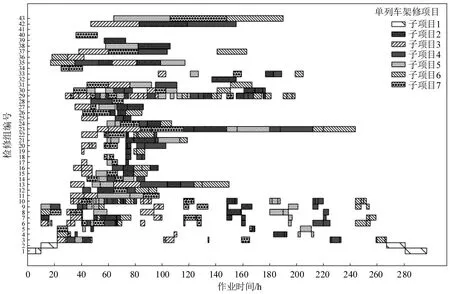
图3 灵活工艺下的单列车大修作业调度优化方案Fig.3 Optimum overhaul repair schedule for a single-train operation using flexible process

(1)不同检修工艺优化效果分析

4种不同工艺下的单列车架修和大修调度方案优化结果如表3所示。

表3 单列车架修、大修调度方案优化结果Table 3 Solution results from optimum overhaul and unwheeling repair schedules for a single-train

不同的检修策略对调度方案的作业效率影响显著。例如工艺场景1与工艺场景2和工艺场景3，采用阶梯式和灵活检修策略的调度方案相对于整体同步策略，架修项目库内作业时间分别下降了5.0%和6.2%，大修项目库内作业时间分别下降10.4%和12.4%。不同的作业流程对调度方案的作业效率影响也十分显著。例如工艺场景3 和工艺场景4，相同的检修策略下，灵活作业流程相对于固定作业流程，架修和大修调度方案的库内作业时间分别减少了10.3%和15.9%。

采用灵活工艺(灵活检修策略+灵活作业流程)可提高架大修调度方案的效率，相比传统的整体同步式作业，库内作业时长分别减少了15.9%和26.3%。在活动数量相同的情况下，增加同步作业活动可显著减少库停时间。4 种工艺下，架大修调度方案中各时段并行作业的活动数量分别如图4和图5所示。

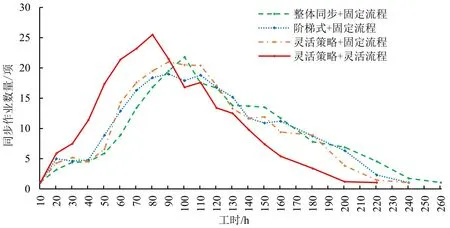
图4 不同工艺下的架修方案各时段同步作业数量Fig.4 Number of synchronous operations in unwheeling repair schedules under different processes

图5 不同工艺下的大修方案各时段同步作业数量Fig.5 Number of synchronous operations in overhaul repair schedules under different processes

由图4和图5可知，灵活工艺(工艺场景4)与其他3 种工艺相比，折线整体偏左且峰值最高，说明采用灵活工艺显著增加了同步作业的数量，缩短了作业时间，提高了作业效率。进一步比较采用固定流程的工艺场景1～3，整体同步策略(工艺场景1)的折线整体偏右，表明该工艺作业效率相对较低和作业时间较长，其主要原因是部分先行完成维修任务的车辆在进入下一检修线前需等待其他车辆。

(2)单列车作业瓶颈分析

作业调度问题中的瓶颈识别通常选用作业设备的平均活跃时间和利用率等指标[6]，指标高的作业设备通常为调度方案中的瓶颈点。在架大修作业中，存在多个同类检修组，识别维修作业瓶颈时应选取若干个检修组的平均作业(活跃)时间；利用率则通过检修组平均作业时长和总作业时长的比值表示。各检修组的平均作业时长如图6所示。

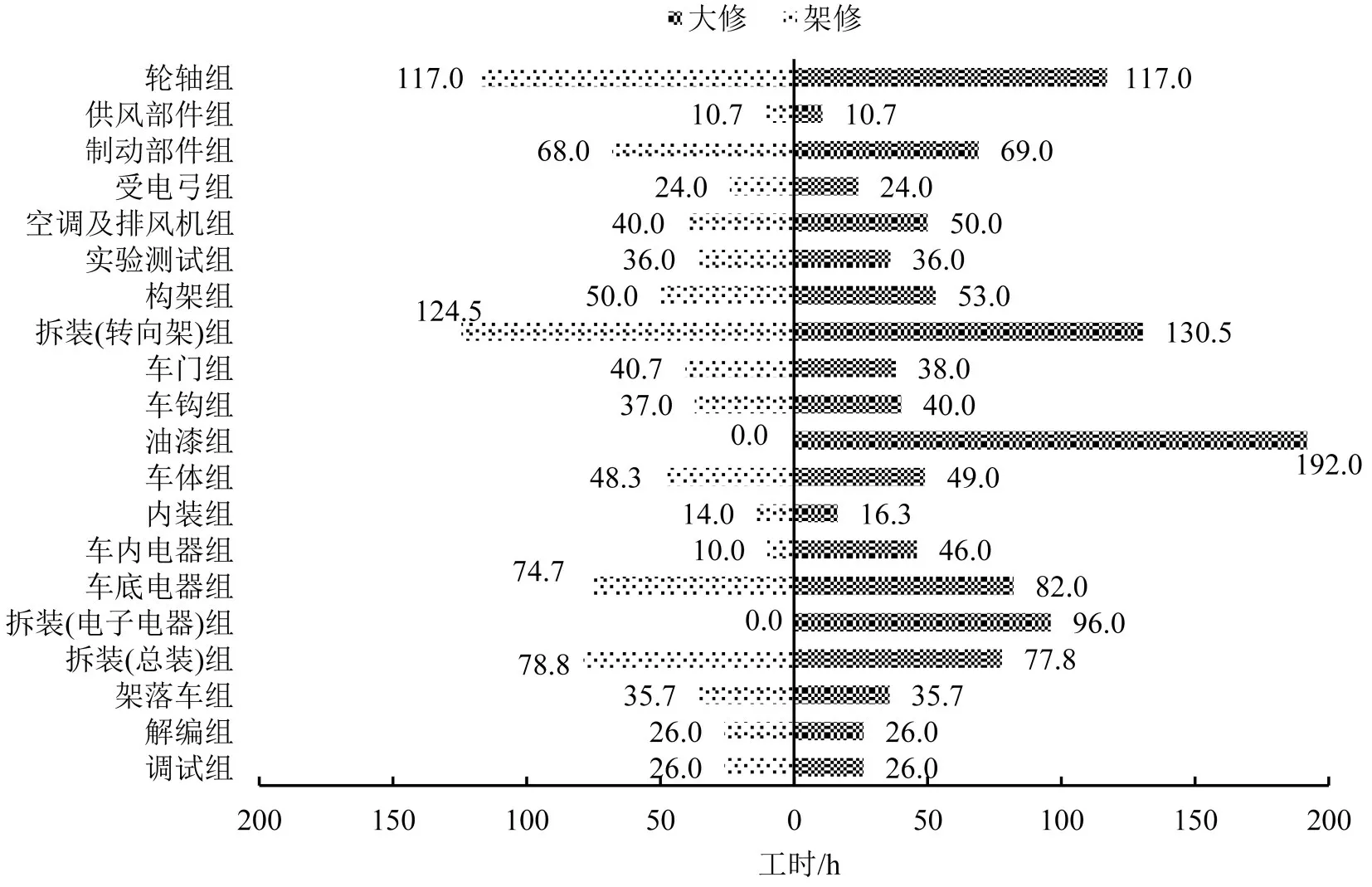
图6 各类检修组平均作业时长Fig.6 Average operating times by maintenance teams

架修作业中，拆装(转向架)组和轮轴组为作业瓶颈，平均作业时长分别为124.5 h和117.0 h，利用率分别为43.9%和64.7%；大修作业中，油漆组和拆装(转向架)组为作业瓶颈，平均作业时长分别为192.0 h 和130.5 h，利用率分别为57.4%和53.9%。相反，部分检修组平均作业时长较短，利用率较低。例如供风部件组和内装组组均利用率均不足10%。不同检修组作业时间之间存在显著的不均衡性，有必要调整设置检修组数量。例如将部分供风部件组和内装组改设为拆装(转向架)组、轮轴组和油漆组，可缓解作业瓶颈，提高整体作业效率。

4.3 双列同步架大修作业调度优化

当架大修车辆段任务量较多时，需同时组织多列车进行架大修作业。设置双列车同步进行架大修的场景，采用混合作业模式，应用本文优化模型及算法获得的结果如表4所示。

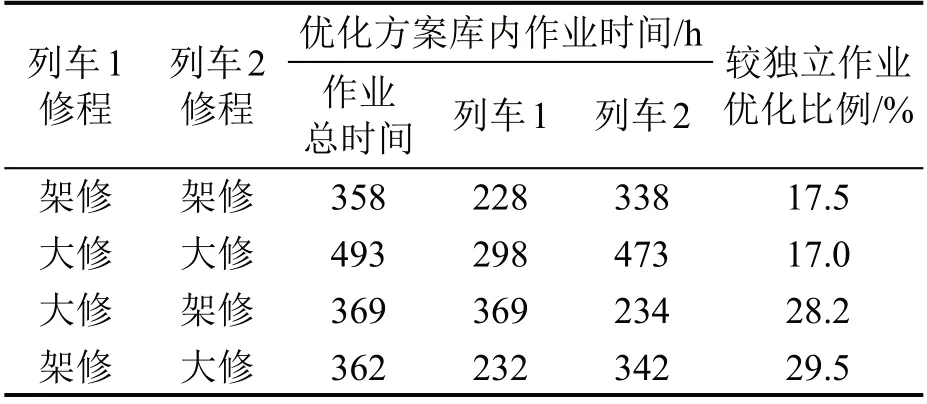
表4 双列架大修作业调度优化方案优化结果Table 4 Solution results from optimum unwheeling and overhaul repair schedules for double trains

表4给出4种同步作业场景下得到的调度方案的作业时间。为区分两列车的作业过程，将列车1和列车2 入库时刻分别设置为第0 h 和第20 h。在两列车同步作业场景下，总库内作业时长较单列车调度方案独立依次作业的时长均有所减少。从不同作业场景的优化比例看，架大修混合的模式优化效果更明显。流水型车间作业效率取决于作业瓶颈位置，由此可知，架大修混合模式相比于其他模式下瓶颈影响有明显减弱。同步作业场景下生成的调度方案中各类检修组的平均利用率如图7所示。

结合表4 和图7 可知，双列车同修程作业同单列作业时的瓶颈位置相似，双列大修的瓶颈为拆装(转向架)组和油漆组，双列架修为拆装(转向架)组及轮轴组；双列车不同修程作业则融合了两种修程下作业的特点，架大修混合作业的瓶颈为拆装(转向架)组和轮轴组。上述瓶颈位置差异的主要原因是转向架系统的检修在架修和大修中都是较繁重的作业内容，而油漆作业只存在于大修修程中，所以，混合作业时油漆组的作业压力降低。

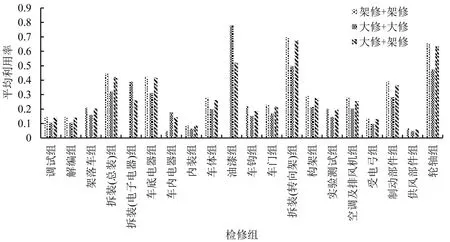
图7 不同作业场景下调度优化方案各类检修组利用率Fig.7 Average utilization of maintenance teams in optimum schedules in different scenarios

混合作业场景下作业瓶颈所在检修组的作业时间不均衡系数(瓶颈位置检修组的平均作业时长与所有检修组平均作业时长的比值)如表5 所示。不均衡系数与1 的差值越大，不均衡程度越强，整体作业效率越低。差值1和差值2为架大修混合作业相对于双列架修和双列大修作业下检修组时间不均衡系数的差值。

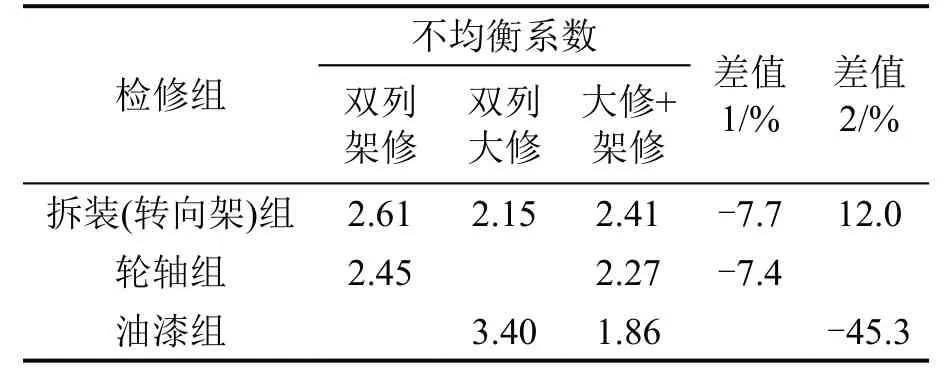
表5 不同作业场景下瓶颈位置作业时间不均衡系数Table 5 Unbalance coefficient of operation time at bottleneck locations in different scenarios

由表5 可知，与双列架修相比，架大修混合作业瓶颈位置拆装(转向架)组和轮轴组的作业时间不均衡系数均有所降低；与双列大修相比，其瓶颈位置拆装(转向架)组的作业时间不均衡系数增加12%，但油漆组的作业时间不均衡系数降低45.3%，整体呈下降趋势。总体上，架大修混合模式下调度方案的瓶颈问题有所缓解，作业效率获得提高。

5 结论

本文得到的主要结论如下：

(1)提出的灵活检修工艺可扩大调度方案优化空间，通过增加并行作业可有效减少列车架大修作业的库内作业时间，与目前大架修作业中常用的移位作业工艺(阶梯式)相比，可分别节省11.4%和17.7%的库内作业时间。

(2)在双列同步作业的情况下，采用不同修程混合维修的模式，可有效降低瓶颈影响，与单列维修模式相比作业效率提高约29.0%。

本文主要对单一架大修线条件下的检修工艺优化问题展开研究，并考虑了多种检修设备能力的影响。后续研究将进一步分析架大修线数量变化条件下灵活工艺对大架修作业效率的影响。