融合网络拓扑结构特征与客流量的城市轨道交通关键节点识别研究

王亭，张永*，周明妮，鲁文博，李世豪

(1.东南大学，交通学院，南京 211189；2.长安大学，运输工程学院，西安 710064)

0 引言

截至2021年底，我国内地城市(不包含港澳台)轨道交通运营里程达到7253.73 km，其中，上海、北京和广州排名前三，轨道交通成网的城市不断增加。在“碳中和”“碳达峰”“出行即服务(MaaS)”等政策及规划的要求和指引下，轨道交通在城市交通系统中扮演的角色愈发重要。然而，设备故障和自然灾害等突发情况会对轨道交通系统的运营造成严重威胁和后果。因此，运用科学的方法识别轨道交通网络的关键节点，进而针对关键节点加强管理，做好应急措施，保障轨道交通网络的安全高效运行，具有重要意义。

近年来，轨道交通关键节点识别以及延伸的网络脆弱性和可靠性研究受到了学者的重视。马超群等[1]将客流需求特性集成到网络脆弱性计算中，以站点故障条件下乘客有效路径子图和网络客流损失率为评价指标，识别了轨道交通关键节点。陈峰等[2]根据节点度、点介数和边介数这3 个指标值的大小，分别评价轨道交通网络节点的重要性，以节点失效下平均最短路径和最大连通子图的变化为基础，分析网络的可靠性。谌微微等[3]识别了点度中心性(节点度)、接近中心性和介数中心性(介数)这3 个指标下的重庆市轨道交通关键节点。杜斐等[4]基于Space L 方法构建上海市轨道交通网络拓扑结构模型，分析该网络在随机攻击和蓄意攻击下的网络效率变化，研究网络的鲁棒性并识别了关键节点。薛峰等[5]以网络拓扑结构指标、脆弱性指标、客流指标和机会指数指标为基础，构建关键节点评价指标体系，应用灰色关联和逼近理想解法识别成都市轨道交通的关键节点。MENG等[6]选取度中心性、接近中心性、介数中心性和特征向量中心性这4 个指标，利用主成分分析法确定各指标权重，进而用因子分析法识别深圳市轨道交通的关键节点，并比较了Space L和Space P模型中拓扑复杂性的差异。WU等[7]提出一个基于节点度的节点占用率指标评价轨道交通节点的利用率水平，根据该指标识别北京、伦敦、巴黎、香港、东京和纽约这6个轨道交通网络的关键节点。KOPSIDAS等[8]以介数中心性、接近中心性和加权节点度这3个指标为基础构建一个新的指标，评价轨道交通网络节点的重要性。轨道交通线网本身是一个物理网络，通过网络拓扑结构典型指标评价节点的重要性具有一定的意义，但这些指标仅能反映节点某个角度的重要性，评价结果并不全面。网络中的节点既在局部发挥着向外传输信息和能量的作用，又在全局中影响着信息和能量的传输效率，在评价节点的网络拓扑结构重要度时，应综合考虑节点的局部重要性和全局重要性。同时，轨道交通节点承担着高效运输客流的任务，客流量是影响其重要性的关键因素。客观合理的评估轨道交通节点的重要性，除了需要考虑节点的网络拓扑结构特征，还需要考虑客流量的影响。

本文提出一种融合网络拓扑结构特征和客流量的节点重要性评价方法，构建轨道交通关键节点识别模型。通过计算节点失效情况下，轨道交通网络性能的变化分析关键节点的影响，为轨道交通的运营维护及轨道交通与其他交通方式的接驳规划等提供参考。

1 复杂网络概念及典型指标定义

对于一个无向无权网络可以表示为G(V,E)，其中，V={v1,v2,…,vn} 为网络G中的节点集合，E={e1,e2,…,em} 为网络G中的连边集合，网络的节点数为n，连边数为m。设网络G的邻接矩阵为B，如果网络中的两个节点vi和vj之间存在连边，则邻接矩阵中对应的元素Bij=1，否则Bij=0。

(1)节点度

节点vi的节点度D(vi)为网络中与节点vi存在连边的节点数，即节点vi的邻居节点数量[9]。该指标能反映节点在网络中的对外传输能力，节点度值越高，其邻居节点数量越多，节点对外传输能力越强，代表的是节点在网络中的局部重要性。计算式为

(2)节点效率

节点效率Ii反映的是节点vi到达网络中其他节点的难易程度，即节点在网络中的传输效率，表征的是其在网络中的中心化水平[10]。节点效率值越大，则其位于网络的中心程度越高，在网络中的传输效率越高，代表的是节点在网络中的全局重要性。计算式为

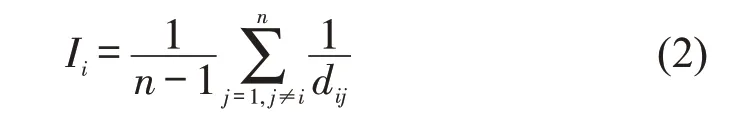
式中：dij为节点vi和vj之间的最短路径长度。

(3)网络效率

网络效率E反映的是整个网络G的传输效率，网络效率值越大，传输难易程度越低，传输效率越高，可以用来衡量网络性能[10]。计算式为

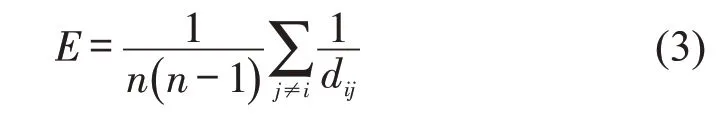
(4)连通度

连通度γ的定义为：网络部分节点失效时，剩余节点形成的连边数er与网络完好时连边数emax的比值[5]，值越大，表明剩余节点组成的网络较完整，网络的性能损失越小。计算式为

(5)最大连通子图

最大连通子图指的是网络中能分解出的节点之间相互连通的最大的网络图。一般用相对最大连通子图J表征部分节点失效后网络性能的变化[5]，值越大，表明剩余节点组成的网络较完整，网络的性能损失越小。计算式为

式中：nr为部分节点失效后，剩余节点组成网络的最大连通子图所包含的节点数；nmax为网络未受损时的最大连通子图所包含的节点数。

2 轨道交通网络关键节点识别模型

2.1 节点网络拓扑结构重要度评价模型

基本思想：节点在网络中的重要性由节点的局部重要性和节点的全局重要性共同决定。本文选取的节点局部重要性指标为节点度，节点度值越大，对外传输能力越强。选取的节点全局重要性指标为节点效率，节点效率值越大，节点的传输效率越高。对于网络中的节点而言，对外传输能力越强，传输效率越高，则节点在网络中的重要程度越高。因此，目标节点的节点度(D)与节点效率(I)的乘积(D×I)越大，节点重要性越高。本文基于该思想构建节点网络拓扑结构重要度评价模型。

需要指出的是，节点的重要性不仅与自身有关，而且与网络中其他节点对该节点产生的影响有关。从局部角度看，某节点的邻居节点的重要性越高，则该节点的重要性高的可能性越大。假设两个节点vi和vj的节点度相等，vi的邻居节点的节点度均大于vj的邻居节点的节点度，则节点vi的重要性会高于vj。从全局角度看，网络中其他节点也会从两个方面对目标节点的节点效率产生影响：一个是其他节点的节点效率大小；另一个是其他节点与目标节点之间的最短路径长度和最短路径的条数。

2.1.1 考虑邻居节点影响的节点度模型

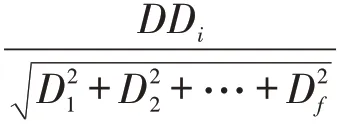
式中：{a,…,k1} 、{b,…,k2} 、{e,…,kn} 表示节点v1、v2、vn的 邻 居 节 点{Va,…,Vk1} 、{Vb,…,Vk2} 、{Ve,…,Vkn} 的 角 标；{Da,…,Dk1} 、{Db,…,Dk2} 、{De,…,Dkn} 为节点v1、v2、vn的邻居节点的节点度。当节点vi与节点vj相邻时，δij=1；否则δij=0。

进一步的，考虑邻居节点影响的改进节点度计算方法为

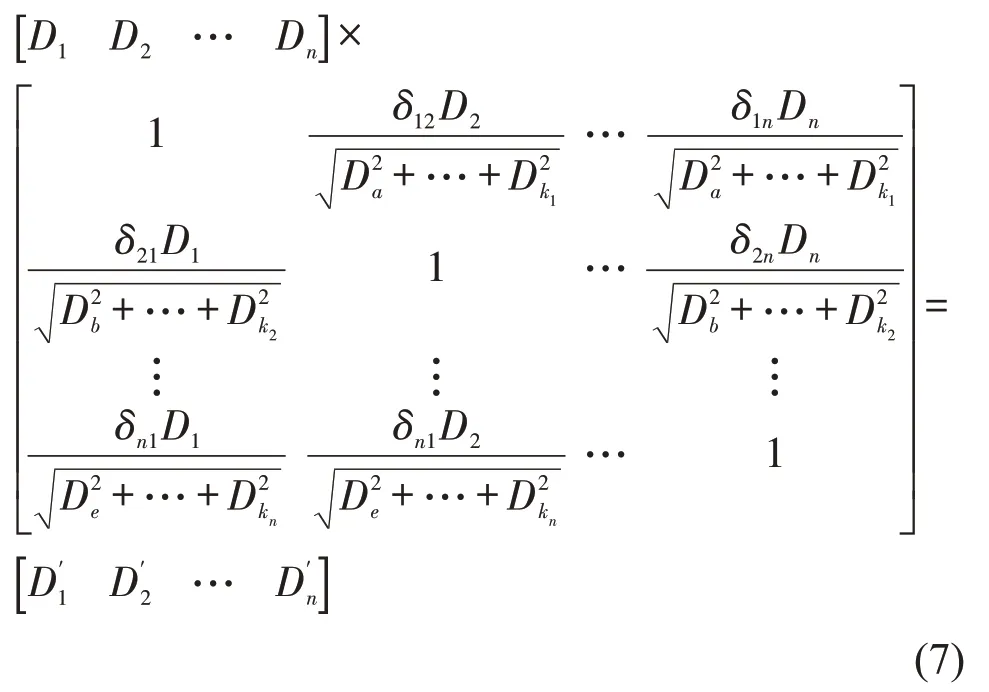
式中：{D1,D2,…,Dn} 为节点{v1,v2,…,vn} 的节点度；{} 为考虑邻居节点影响的节点{v1,v2,…,vn} 的节点度。

2.1.2 考虑其他节点影响的节点效率模型

节点效率是全局性指标，应在网络全局范围内进行考虑。某节点与重要性高的节点之间的最短路径越短，最短路径条数越多，则该节点的重要性高的可能性越大。因此，网络中其他节点对目标节点的节点效率的影响由其他节点的节点效率，其他节点与目标节点间的最短路径长度，以及其他节点与目标节点间的最短路径的条数决定，并且与其他节点的节点效率值成正比，与其他节点与目标节点间的最短路径长度成反比，与其他节点与目标节点间的最短路径条数成正比。本文认为某节点vj对目标节点vi的节点效率的影响系数为，cij为节点间最短路径条数。网络中任意节点对其他节点的节点效率的影响系数矩阵为

进而，考虑其他节点对目标节点影响的改进节点效率计算方法为

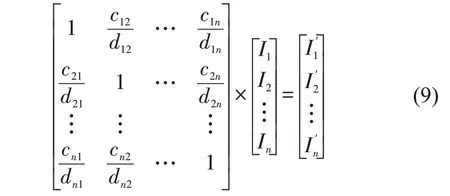
式中：{I1,I2,…,In} 为节点{v1,v2,…,vn} 的节点效率；{} 为考虑其他节点影响的，节点{v1,v2,…,vn} 的节点效率。

因此，综合考虑其他节点对目标节点影响的节点网络拓扑结构重要度评价模型为

式中：Ni为节点vi的网络拓扑结构重要度，值越大，重要性程度越高；为考虑邻居节点对节点vi影响的节点度；为考虑其他节点对节点vi影响的节点效率。

2.2 节点客流量重要度评价模型

轨道交通节点的客流量大小与节点周边的用地性质、用地开发强度及节点在网络中的位置等多种因素有关，是影响节点重要性的关键指标，节点的客流量越大，其在网络中的重要性越高。本文选取节点进出站客流和换乘客流评价节点的客流量重要度，其中，进出站客流反映的是节点在满足局部出行需求方面所发挥的作用，换乘客流反映的是节点在轨道交通网络不同线路间转运客流的能力，构建的节点客流量重要度评价模型为

式中：Qi为节点vi的客流量重要度；qin为节点vi的进出站客流；qit为节点vi的换乘客流。

2.3 节点综合重要度评价模型

轨道交通节点的重要性既与节点在网络拓扑结构中扮演的角色有关，也与节点在客流运输中所发挥的作用紧密相关。节点的网络拓扑结构重要度是节点在网络的传输能力和传输效率中所发挥作用的集中体现，节点的客流量重要度是节点在运输客流和转运客流方面能力的表征，两者共同决定了节点的重要性水平。本文构建的融合网络拓扑结构特征和客流量的节点综合重要度评价模型流程如图1所示。

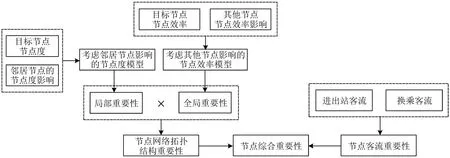
图1 节点综合重要度评价Fig.1 Comprehensive importance evaluation of nodes

融合网络拓扑结构特征和客流量的节点综合重要度评价模型为

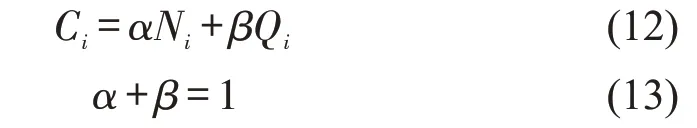
式中：Ci为节点vi的综合重要度；Ni为节点vi的网络拓扑结构重要度；Qi为节点vi的客流量重要度；α为节点网络拓扑结构重要度系数；β为节点客流量重要度系数。在进行节点综合重要度计算时，应将Ni和Qi利用比例法进行归一化处理。

3 实例分析

3.1 西安市轨道交通网络基本特征

截止到2022年6月，西安市共开通运营8条轨道交通线路，分别为1～6号线、9号线和14号线，建成投入使用的站点159 座，其中，换乘站点14 座。本文利用Space L方法对西安市轨道交通网络进行建模，结果如图2 所示。实际生活中，乘客更在意的是运行时间，而由于站点之间距离差异造成的站点间的运行时间差较小，为计算方便，本文假设网络拓扑结构中站点之间连边长度相等。

图2 西安市轨道交通网络拓扑结构Fig.2 Network topology of rail transit in Xi'an

西安市轨道交通的部分网络拓扑结构指标如表1所示。

表1 西安市轨道交通网络拓扑结构特征Table 1 Network topology characteristics of rail transit in Xi'an

3.2 节点客流量分析

客流量是评价轨道交通节点重要性最直观的指标之一，节点客流占网络客流的比例能较好地反映节点在网络中的相对重要程度，2021 年9 月，西安市轨道交通各节点的日均网络客流占比如图3所示。

由图3 可以看出，有5 个节点的网络客流占比大于5%，并且5个节点均是换乘节点，分别是西安北站(43)、小寨站(30)、大雁塔站(50)、五路口站(15)和北大街站(14)，这5 个节点的客流合计占比为34.41%。节点网络客流占比大于2%的节点有11个，客流合计占比为51.68%，表明在西安市轨道交通网络中，少数关键节点吸引和转运了大量客流。

图3 节点客流占网络客流比例Fig.3 Proportion of node passenger flow in network passenger flow

换乘节点在轨道交通网络中通常扮演重要的角色，换乘节点的网络客流占比，以及节点的进出站客流和换乘客流的比例分布情况如图4所示。

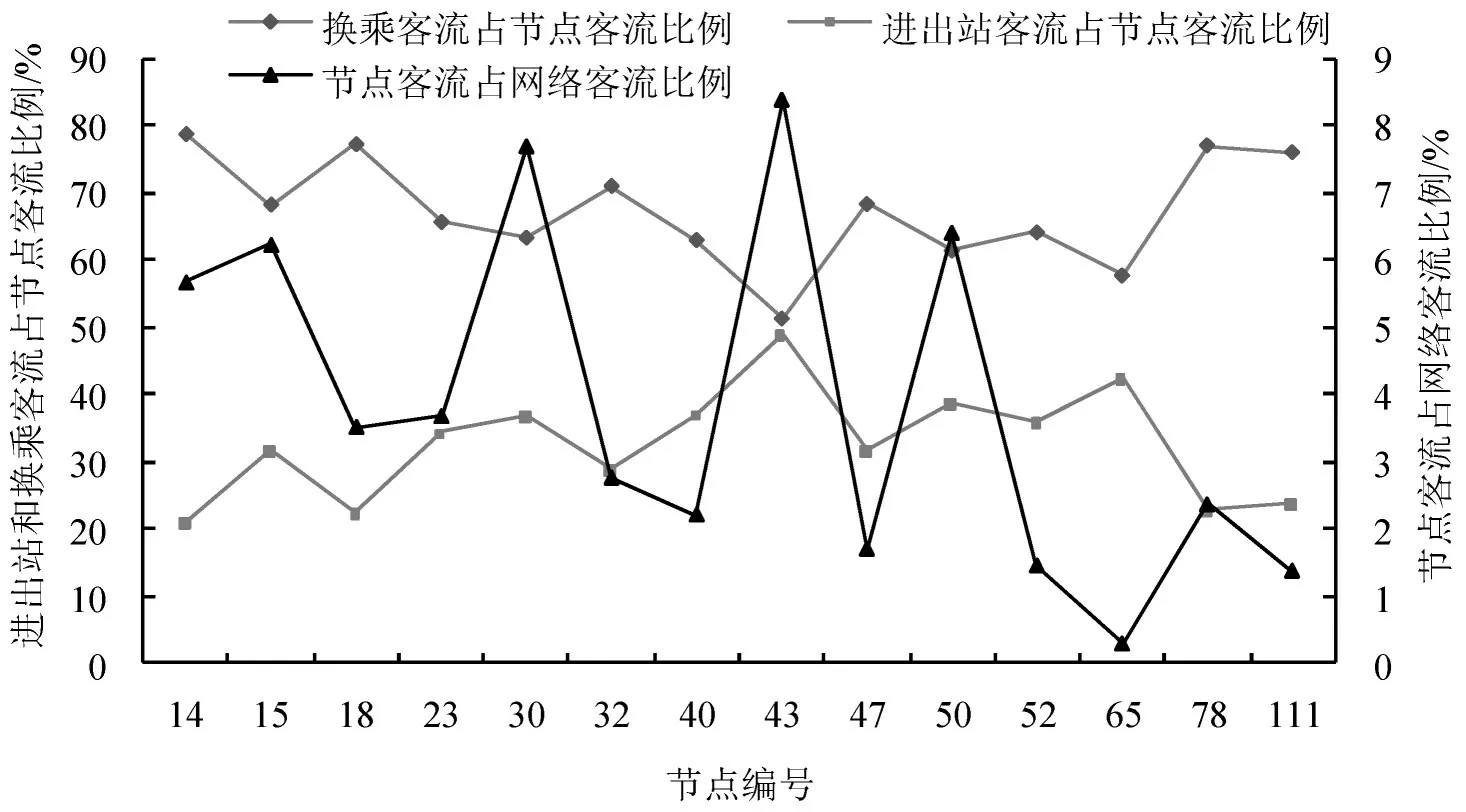
图4 换乘节点客流分析Fig.4 Passenger flow analysis of transfer nodes

由图4可以看出，不同换乘节点之间的网络客流占比差异很大，网络客流占比最大的西安北站(43)与网络客流占比最小的双寨站(65)之间的差值超过了5%。除西安北站(43)和双寨站(65)以外，其他节点的换乘客流占比远大于进出站客流，充分体现了换乘节点的功能特性。西安北站是3 条轨道交通线路的换乘节点，同时，也是城际客流的集散点，因此，换乘客流占比与进出站客流占比差异不大；双寨站的换乘客流比例和进出站客流比例相近，主要是由于双寨站所在的14 号线开通运行时间较短，同时，线路周边的土地利用尚在开发，客流仍在培育当中，待土地开发成熟，双寨站的换乘功能特性有望进一步凸显。

3.3 轨道交通关键节点识别

3.3.1 节点网络拓扑结构重要度

以本文节点网络拓扑结构重要度评价模型为基础，可以得到网络拓扑结构角度的西安市轨道交通重要性排名前30的节点，如表2和图5所示。

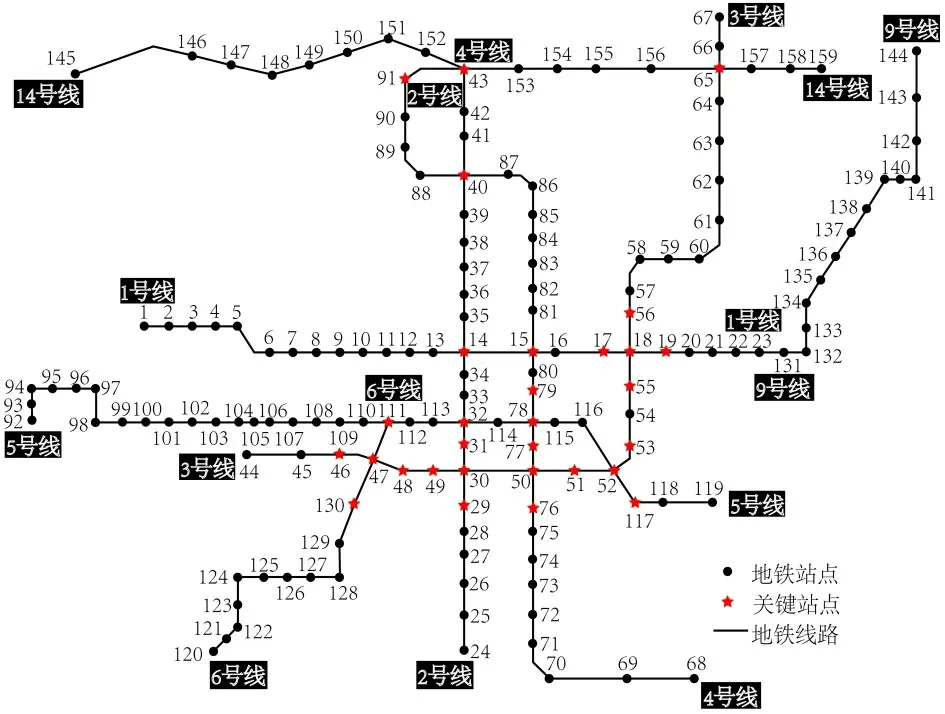
图5 网络拓扑结构关键节点Fig.5 Key nodes of network topology

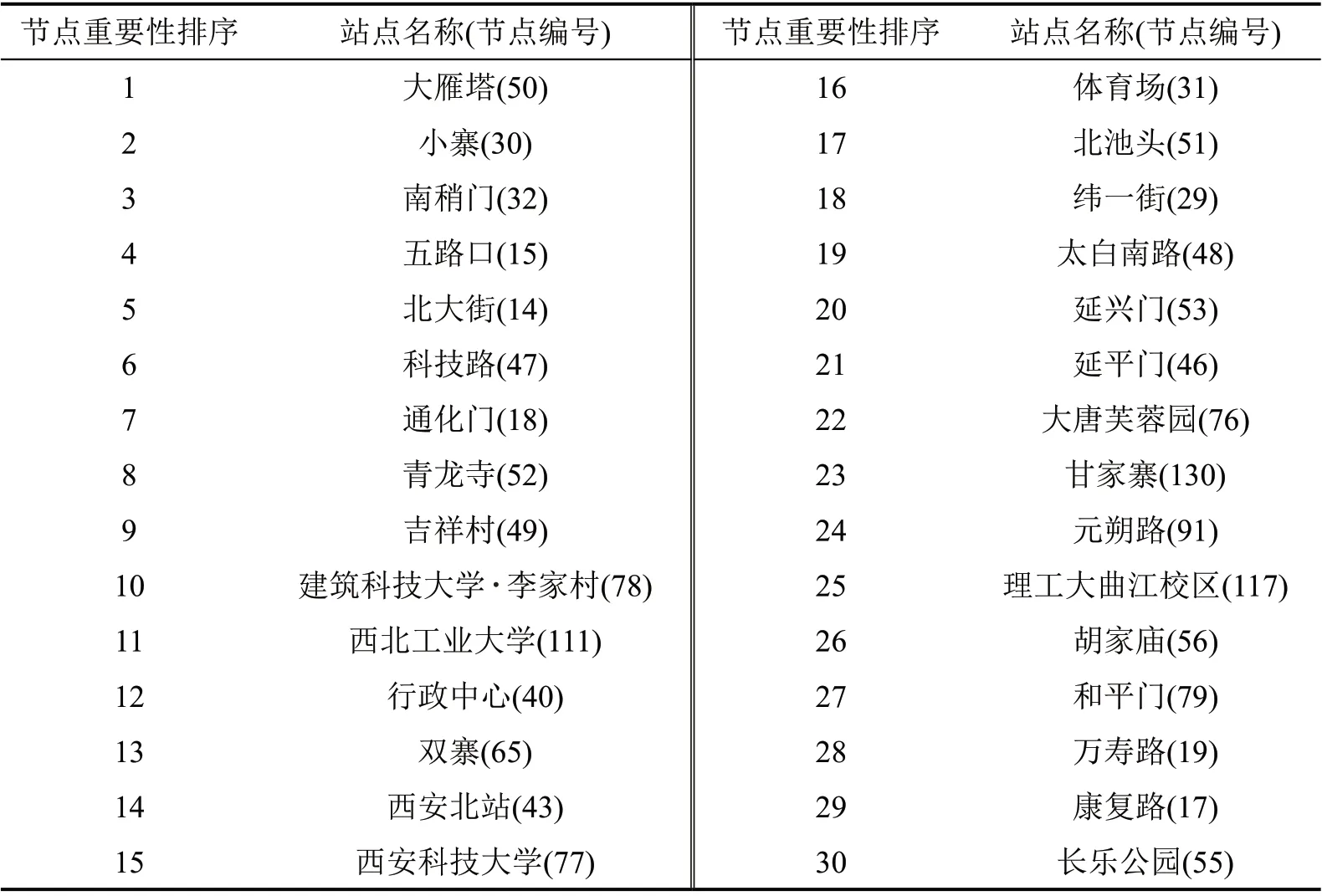
表2 西安市轨道交通网络拓扑结构关键节点Table 2 Key nodes of network topology of rail transit in Xi'an

网络拓扑结构重要度评价模型识别了除纺织城站(23)以外的所有换乘节点，这是由于纺织城站是1 号线和9 号线的共线换乘节点，网络拓扑结构重要度不明显。同时，由图5 可知，从网络拓扑结构角度看，线路之间的换乘站点，以及有助于不同线路形成闭合环路的部分节点，在轨道交通网络中起至关重要的作用。

3.3.2 节点客流量重要度

以本文节点客流量重要度评价模型为基础，可以得到客流角度的重要性排名前30的节点，如表3和图6所示。

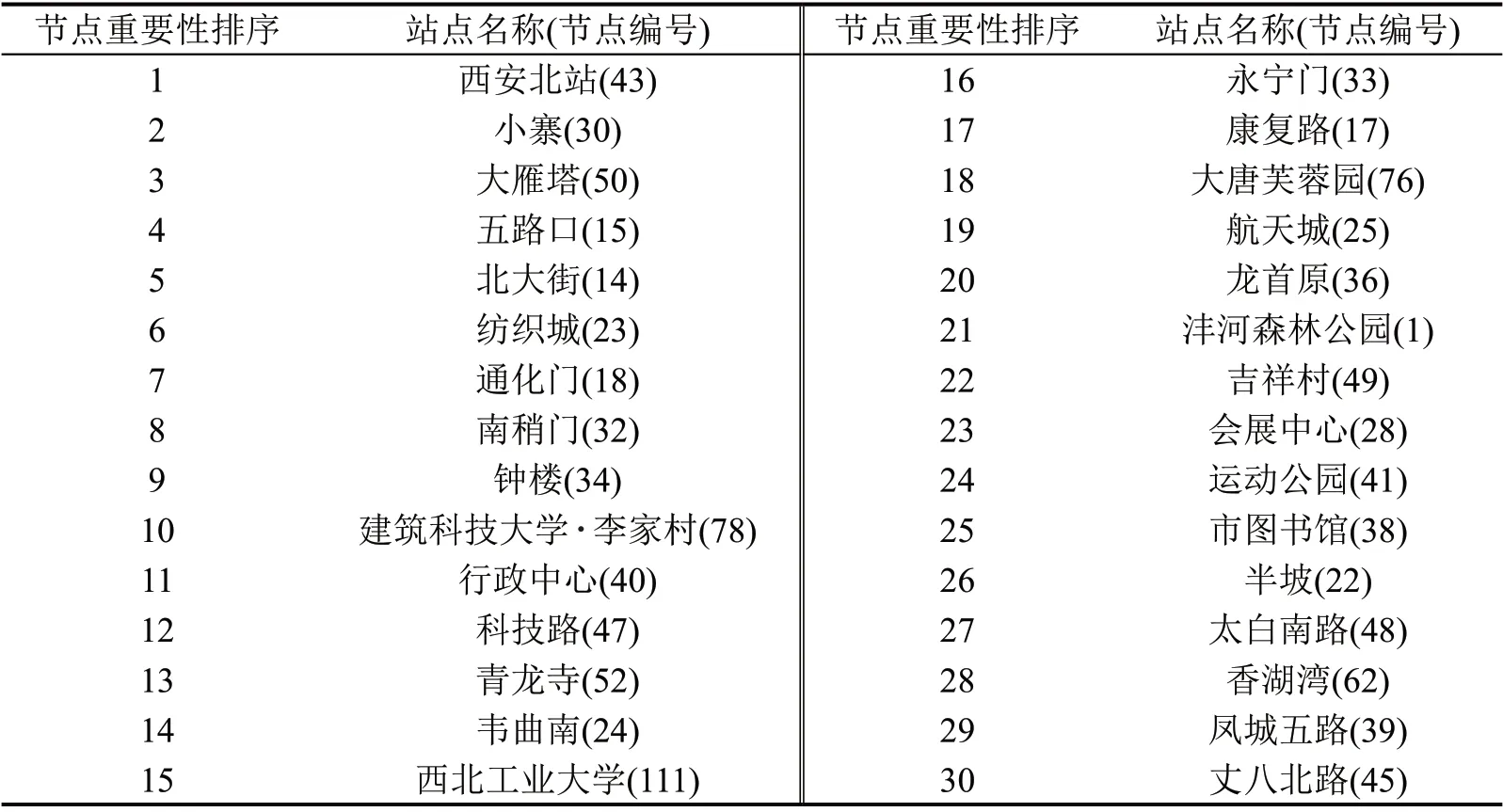
表3 客流视角下的关键节点Table 3 Key nodes from perspective of passenger flow

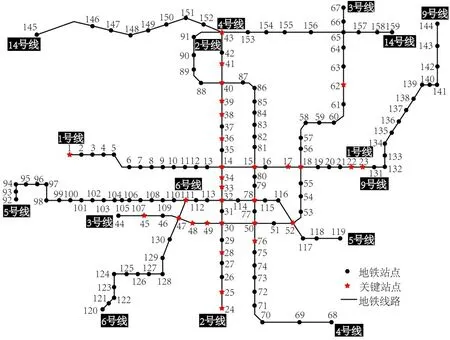
图6 客流视角下的关键节点Fig.6 Key nodes from perspective of passenger flow

由图6可以看出，基于节点客流量的关键节点与网络拓扑结构角度的关键节点之间有16个重合节点，表明这16个节点无论在网络拓扑结构中，还是在客流运输中，均扮演重要角色。节点客流量视角下的关键节点更突出了节点在满足居民出行需求方面的功能性，典型的位于城市外围出行需求量较大，但网络拓扑结构重要度较差，例如韦曲南站(24)、航天城站(25)和沣河森林公园站(1)，以及位于城市中心区出行需求旺盛的景点和商圈附近，例如永宁门站(33)和钟楼站(34)等。节点客流量重要度模型识别出了除双寨站(65)以外的所有换乘节点，这是由于双寨站是3 号线和14 号线的换乘车站，14号线位于城市外围，目前，线路周边的土地利用和开发强度较低，仍在发展之中，待线路周边土地开发成熟，客流培育完成，模型能较好识别该节点。

3.3.3 节点综合重要度

节点的综合重要度不仅取决于节点的网络拓扑结构重要度和客流量重要度，而且与两者的权重紧密相关，权重的取值受轨道交通管理目标、轨道交通网络结构及其客流特征、城市布局、城市交通结构以及城市交通发展目标等多种因素的影响。本文仅从轨道交通管理目标的角度进行讨论，节点的网络拓扑结构权重分别取0.4，0.5和0.6这3种情景。当网络拓扑结构权重取值为0.4 时，轨道交通的管理目标更侧重于保障客流的运输，西安市是一个热门旅游城市，该情景更适用于节假日情况下的关键节点识别，以及对应的节点维护策略和应急管理方法的制定，以保证重点区域的交通系统稳定。当网络拓扑结构权重取0.6 时，轨道交通的管理目标更侧重于保障网络的有效性和通达性，该情景更适用于特殊天气(例如暴雨和大雪等)或特殊事件(电力紧张或停电)下的关键节点识别。网络拓扑结构权重取0.5 时，更适用于日常情况下的关键节点识别。

不同权重网络拓扑结构重要度和客流量重要度下的节点重要性排名如表4所示，关键节点在轨道交通网络中的位置如图7所示。

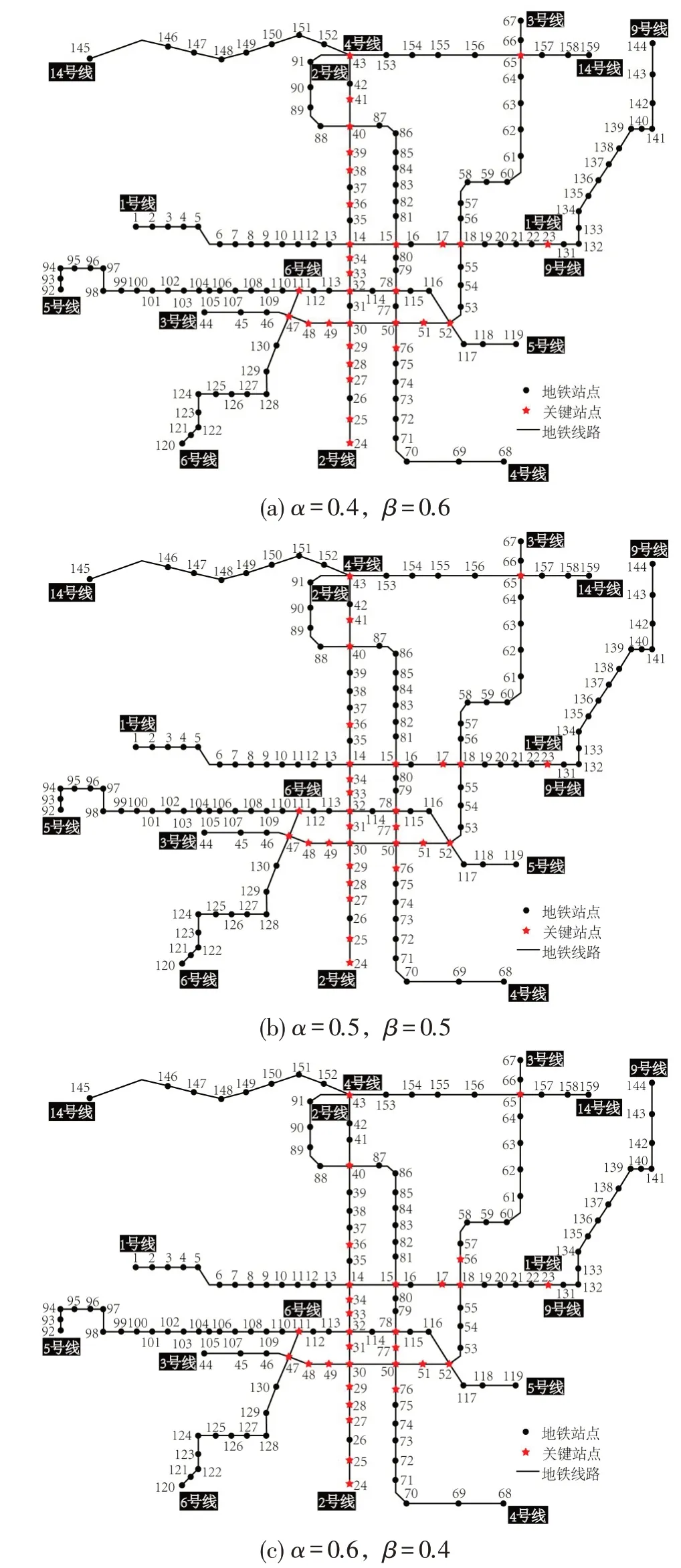
图7 不同指标权重下轨道交通关键节点Fig.7 Key nodes of rail transit under different weights of indicators

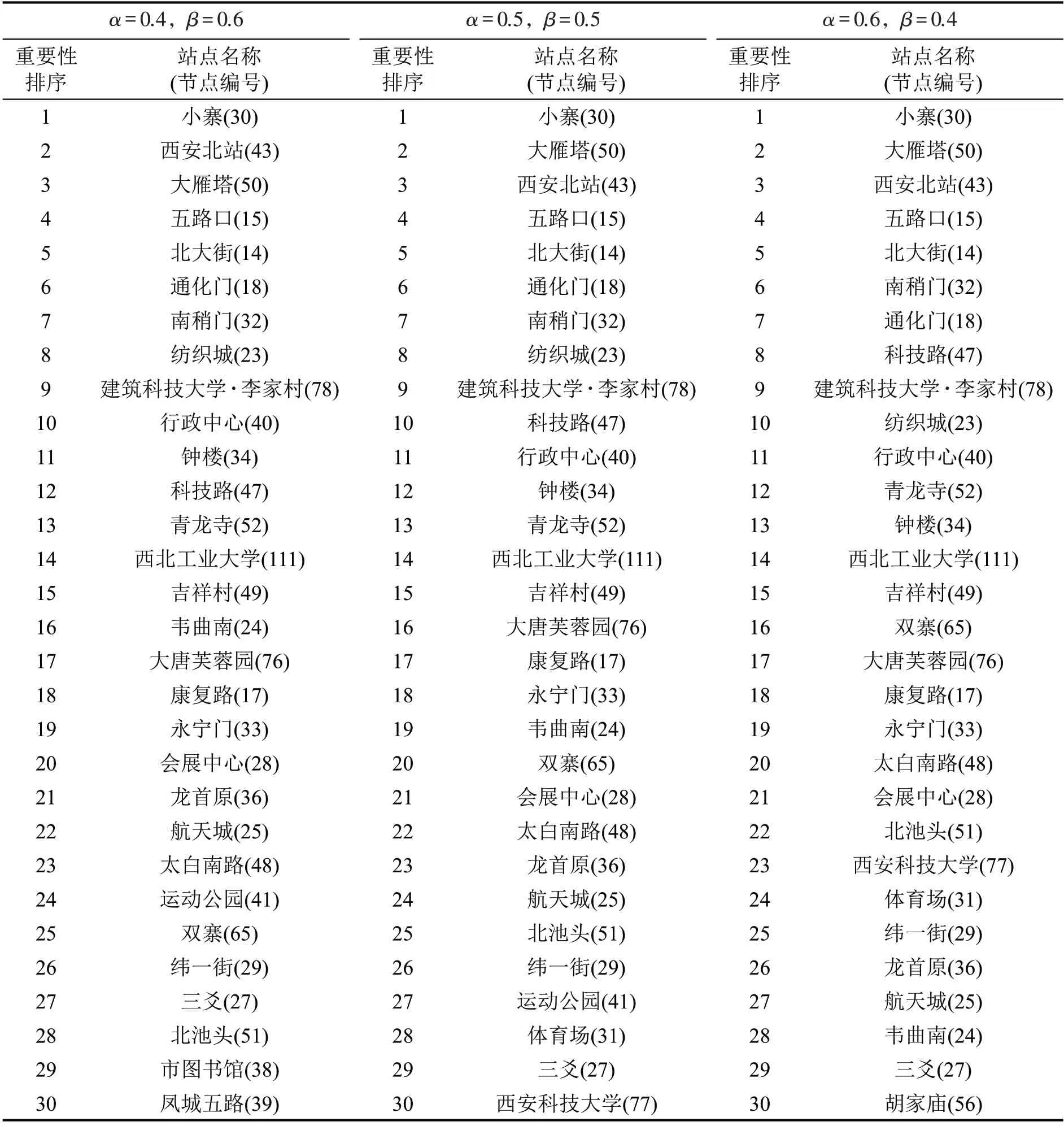
表4 不同指标权重下西安市轨道交通关键节点Table 4 Key nodes of rail transit in Xi'an under different weights of indicators

由表4可以看出，不同指标权重下轨道交通网络的关键节点重合度非常高，共同的关键节点高达27 个，对于这些节点的运营维护应作为重中之重。本文提出的关键节点识别模型，较好地综合考虑了节点的网络拓扑结构特征和客流量，成功识别了换乘客流较大但网络拓扑结构重要度不明显的共线换乘节点-纺织城站(23)，网络拓扑结构重要度较高但客流仍在培育中的换乘节点-双寨站(65)，以及出行量大但位于城市外围的韦曲南站(24)和航天城站(25)，表明模型具有良好的适应性。3 种权重下的关键节点差异主要体现在运动公园站(41)、市图书馆站(38)、凤城五路站(39)、体育场站(31)、西安科技大学站(77)和胡家庙站(56)。其中，运动公园站、市图书馆站和凤城五路站的客流量明显高于其他节点，而体育场站、西安科技大学站和胡家庙站的网络拓扑结构重要度较高，导致不同指标权重下的关键节点差异。

3.4 关键节点失效对网络的影响分析

科学评估关键节点失效对轨道交通网络运行的影响，可以更好的为轨道交通维护策略和应急处理方案的制定提供参考。本文选取网络效率、连通度和相对最大连通子图衡量节点失效对网络结构所产生的影响，选取客流损失衡量对网络客流的影响。对关键节点按重要性排名进行蓄意攻击，得到轨道交通网络性能变化，如图8 所示。由图8 可以得到以下结论：

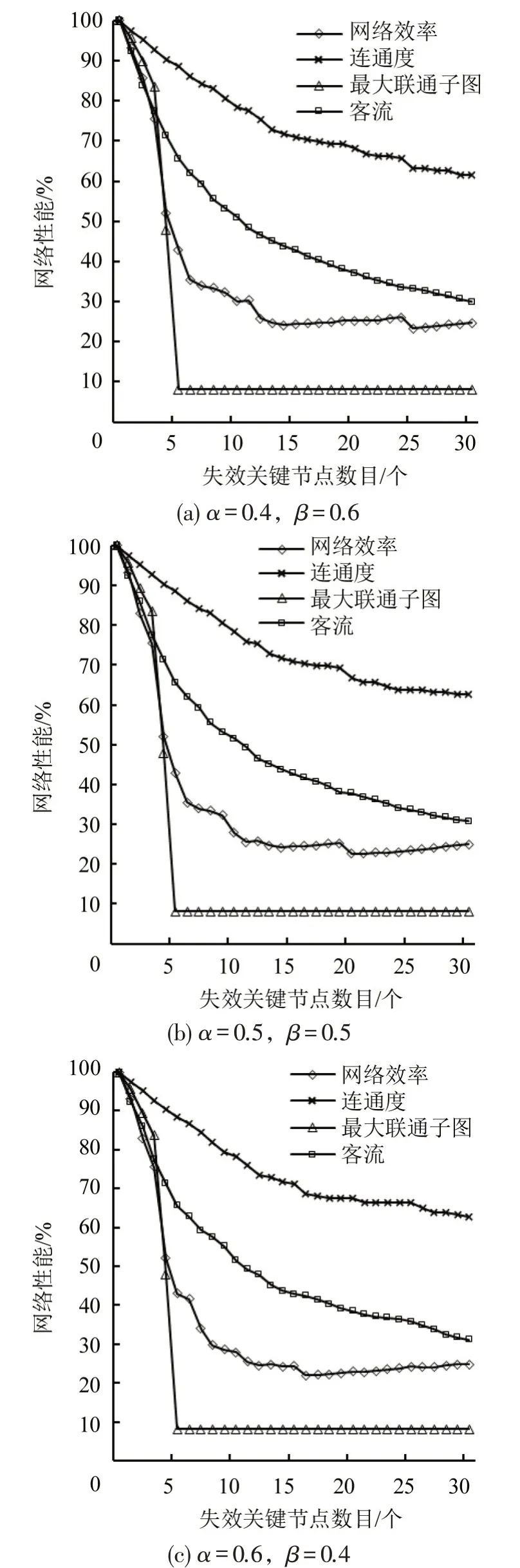
图8 关键节点失效下的网络性能变化Fig.8 Change of network performance when some key nodes failed

(1) 排名前5 的节点(小寨站(30)、西安北站(43)、大雁塔站(50)、五路口站(15)和北大街站(14))失效，会对轨道交通网络的结构和性能造成严重破坏，网络客流会损失34.41%，网络效率会降低57%，相对最大连通子图比例会下降91.82%，表明模型对关键节点的识别效果较好。

(2)3 种权重下轨道交通网络的相对最大连通子图最终降低到一个相同的稳定水平，并且均是需要失效5个关键节点。

(3)不同指标权重下排名前7 的节点虽然重要性排序不同，但节点完全相同，这7个节点失效后，网络效率会降低65.96%，随着失效节点继续增多，网络效率的下降速率会明显降低并逐渐趋于稳定。整体而言，α=0.4 时，网络效率降低最慢；α=0.5 时，居中；α=0.6 时，网络效率降低最快。

(4)不同指标权重下轨道网络连通度的整体变化趋势相似，变化幅度相近。

(5)不同指标权重下客流损失变化趋势相似，当α=0.4 时，客流损失率最大；α=0.6 时，客流损失率最小。

4 结论

本文得到的主要结论如下：

(1)节点的网络拓扑结构重要度由节点在网络中所发挥的作用以及其他节点对该节点产生的影响共同决定。利用考虑邻居节点影响的改进节点度模型和考虑其他节点影响的改进节点效率模型评价节点的局部重要性和全局重要性与实际情况更相符，能更好区分节点度和节点效率相同的节点的重要性，有效提升评价结果的辨识度；所构建的基于传输能力和传输效率的节点网络拓扑结构重要度评价模型，能较全面客观地反映节点的网络结构重要程度；模型的实例应用结果表明：不同线路之间的换乘节点，以及有助于不同线路形成闭合环路的节点，在轨道交通网络拓扑结构中起关键作用。

(2)所构建的轨道交通关键节点识别模型，融合了节点的网络拓扑结构特征和客流量，能更科学全面地评估节点重要性，有助于决策者制定更有效的针对性管理措施保障轨道交通的有序运行；识别出的关键节点能很好地反映其功能特性，模型具有良好的适应性；实例应用结果显示，识别出的西安市轨道交通排名前5的节点失效，会对网络的结构和性能造成严重的破坏，证明了模型的有效性。