重型货运车辆出行时空差异性和影响因素分析

陈小鸿，刘涵，张华，杨志伟

(同济大学，a.道路与交通工程教育部重点实验室；b.磁浮交通工程技术研究中心，上海 201804)

0 引言

高效管理城市货运交通事关社会经济发展效率和居民生活成本。货运交通量增长带来货运交通重要性提升，随着城市发展品质要求的日益提高，使得货运交通尤其是重型货运交通管理日益成为城市交通安全、排放和污染等综合治理领域的重点工作。高效精准的管理货运交通需要全面理解和认识货运交通运行的时空特征和影响因素等问题。对比客运交通，货运交通尤其是重型货运交通无论是理论研究还是应用研究都十分匮乏[1]。造成货运交通研究不足的局面主要有两方面原因。一方面，在安全、环境和噪声等交通负外部性未引起足够重视的时代，货运交通因为其相对客运交通而言交通量占比较小，未被认为对城市交通运行具有重要影响，吸引的研究关注不够。另一方面，货运交通本质是经济生产行为在流通领域的体现，是物资流通链上的多元主体(货主、承运商、货车司机及零售商等)经济行为的决策结果，并不是个体生活行为的呈现，使得交通研究中最为常见的人口-土地利用、居民出行调查及手机信令等基础数据几乎完全不能支持对货运交通开展深入研究，使货运交通领域研究基础十分薄弱。

随着信息技术应用普及和对货运交通尤其是重型货运交通治理要求的提高，世界范围内对货运交通车辆全过程位置数据监测日益普及，为货运交通研究开辟了新途径[2]。近3～5年来，基于货运车辆位置数据(GPS)分析货运需求特征和车辆运行特征等相关研究逐渐兴起。SIRIPIROTE 等[3]论证了利用货车GPS数据分析货车出行与活动特征、活动模式以及出行链的可行性。利用GPS 数据开展货运交通研究的关键技术问题之一是如何切割轨迹数据构建车辆出行数据，ADMA 等[4]基于30 s 采集间隔的3.5 t以上货车GPS数据，通过灵敏度分析方法确定10 min的时长阈值切割出行；DEMISSIE等[5]提出基于速度阈值的启发式算法识别GPS 轨迹数据的货车停留行为；GINGERICH等[6]构建了距离缓冲阈值方法识别货车停留行为。2014年，交通运输部等部委联合发布《道路运输车辆动态监督管理办法》(简称《管理办法》)，明确要求重型载货汽车(总质量为12 t及货运车辆)全部安装和使用卫星定位装置，为系统研究我国货运交通特别是重型货运交通提供了扎实的数据基础。例如，丁晓青[7]和肖作鹏等[8]基于12 t以上货车GPS数据分析了厦门和深圳重型货运车辆交通特征；甘蜜等[9]从货运出行信息辨识、货运系统关键特征预测以及货运系统应用这3方面综述了货车轨迹数据在公路货运领域中的应用。

回顾现有重型货运车辆交通研究，GPS数据已成为精细化描述车辆出行特征的重要工具，基于轨迹数据提取出行信息是关键技术方法。目前，关于货运车辆出行特征分析主要围绕出行次数和出行距离(或时长)等基本信息开展，也有部分学者关注到了货运交通与设施间的关联性，并分析了大型设施间的货运交通联系[8]。但现有研究的对象较少考虑重型货车分类，货车出行特征应该结合货运行为本身特性开展，例如，不同类型的重型货车轨迹数据的出行切割应该采用不同的时间阈值，以更精准识别重型货车的组内运行差异性，支持更精准的货运交通管理政策的制订与实施。整体而言，有两方面有待改进。其一，重型货运车辆包括多种类型，例如，普通大货车、集装箱卡车、冷链车及土方车等，不同类型重型货运车辆的功能作用和运行机制有着显著差异，既有研究对不同类型重型货车运行特征差异性刻画不足；其二，不同类型重型货车交通时空分布的影响因素差异刻画不足，各类型货车交通量与用地设施间的非线性关系研究不足。基于以上，本文重点刻画重型货车活动的时空分布和影响因素的差异性，弥补既有研究不足。本文讨论了5 类重型货车基于GPS 轨迹数据的出行划分阈值确定方法，分析5 类重型货车的出行次数、时刻分布、空间集聚模式及其差异，并以普通大货车与集装箱卡车为研究对象，利用广义加性模型(Generalized Additive Model, GAM)解析两类车辆活动空间影响因素及差异，捕捉集装箱卡车活动与物流仓储用地规模之间的非线性作用机制。

1 货运车辆出行切分方法

1.1 数据清洗

本文数据源是深圳市4.2 万辆重型货运车辆在2020 年12 月7 日～13 日(一周)的GPS 轨迹数据(车辆ID已匿名化编号处理)，车辆类型包括：普通大货车、集装箱卡车、土方车、冷链运输车和重型罐式车这5 类。GPS 数据采集间隔约30 s，每条记录中包括：时刻、位置、速度及累计行驶里程等信息。原始GPS数据需要进行预处理和清洗，规则为5条：(i)删除时间记录在研究日期之外的数据；(ii)删除完全重复的数据记录(保留第1条)；(iii)删除事件记录字段非0值的数据记录，即发生数据接收错误；(iv)剔除单日数据小于100条的车辆数据，即判定车辆处于非使用状态；(v)剔除里程变化异常的车辆数据，例如，里程跃迁、单日里程变化大于2000 km 等情形。数据预处理和清洗后，5 类车辆的有效样本数量如图1所示。

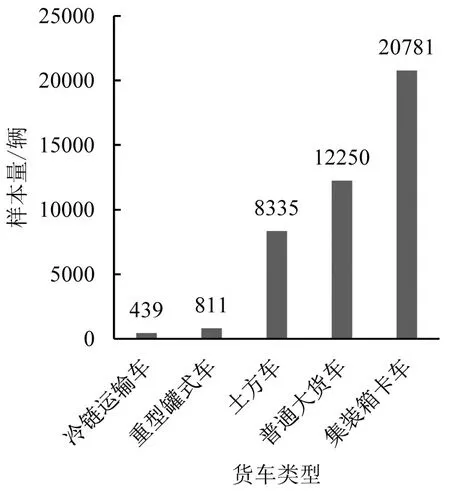
图1 5种类型货运车辆数据样本Fig.1 Sample sizes for five types of freight vehicles

1.2 轨迹数据切割与出行界定

GPS 数据是监测车辆时-空变化的连续数据，如何切割连续数据，界定车辆活动或出行是关键性的基础工作，直接影响车辆活动特征分析和影响因素分析的结论。车辆出行界定的首要工作是从轨迹数据中识别起讫的端点。基于GPS 数据识别起讫端点分为两步：第一步是根据GPS轨迹数据判断车辆是否存在停留及停留位置，第二步是基于停留位置筛选有效停留点。第一步的车辆停留及其位置识别是通过车辆行驶速度或发动机是否熄火等信息识别，第二步的有效停留点识别是技术关键点，主要有地理信息法[10]、空间聚类法[11]以及时间阈值法[12]这3种处理方法。地理信息法通常借助POI信息辅助判断停留类型，需要POI信息全面完整和精细的空间颗粒度才能有较好的正确率；空间聚类法试图找寻车辆轨迹在空间上的高度集中位置表征停留，对轨迹数据的采样频率及精度均有较高要求；结合速度和位置变化的停留时间阈值法运用较为广泛，但难点是对停留时间阈值的确定，现有研究主要通过经验判断确定。

本文数据涵盖多种类型的重型货车，其运行机制和影响因素存在异质性，地理信息法和空间聚类法难以有效刻画，因此，采用时间阈值方法筛选停留点。为捕捉不同类型车辆活动差异性，针对不同类型车辆确定差异化的时间阈值。本文提出两步骤货车出行划分方法。第一步是根据停留时长与速度阈值的组合生成初始停留点集；第二步采用时间阈值法(各类车辆阈值不同)筛选得到有效停留点，将两次有效停留之间的片段提取为1次车辆出行，构建车辆出行数据集，包括每次出行的起讫点及起止时刻等数据字段。货车轨迹切割方法如图2所示。

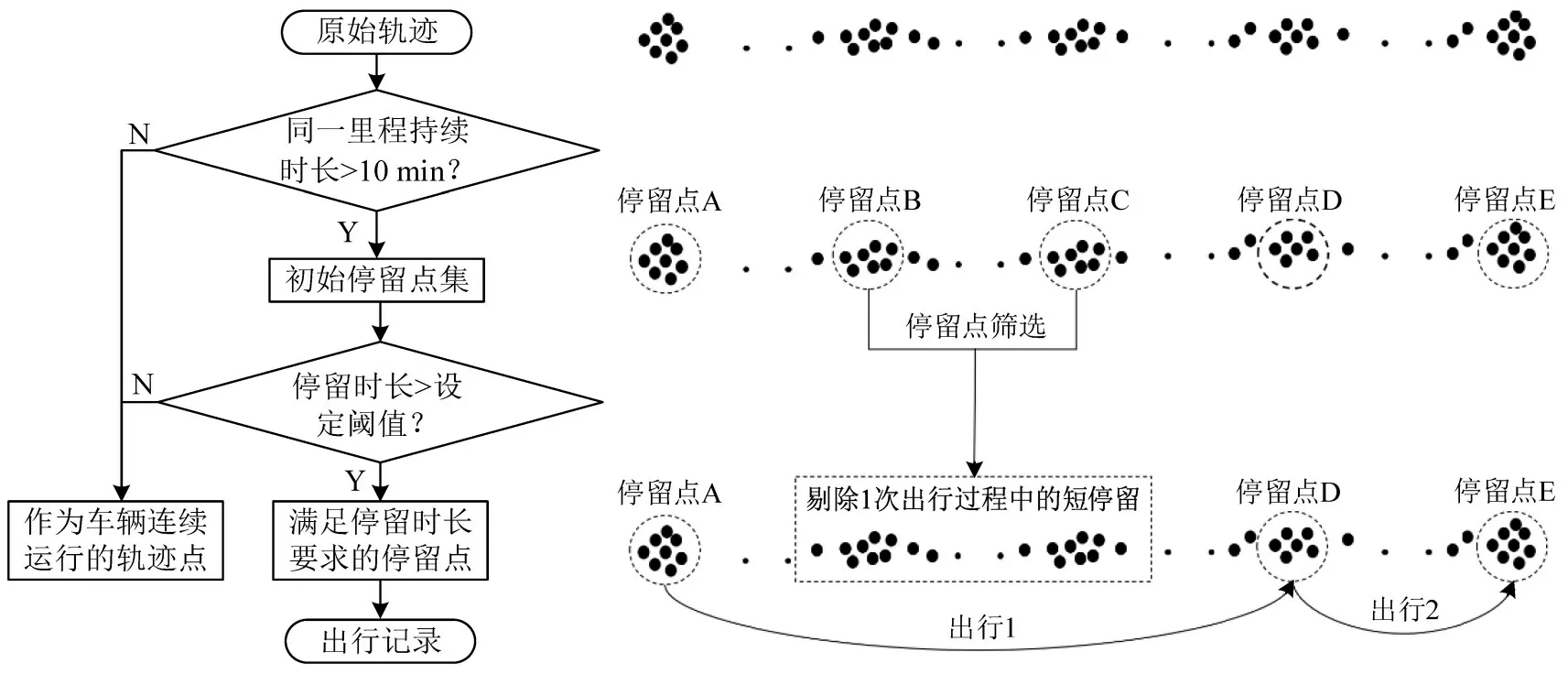
图2 货车轨迹切割方法示意Fig.2 Schematic diagram of truck track cutting method

(1)识别初始停留点集

将一段时间内里程未发生变化视作停留时段，但考虑到某些轨迹数据的跳跃性(例如，两条数据间隔长达几分钟)，因此，以速度阈值作为补充，设置两条识别规则。规则1：若字段‘mileage’(里程)超过10 min 保持不变，判断为停留。现有研究成果表明，10 min作为货车停留事件的判别是合理的[4]，且本文研究对象为12 t以上重型货运车辆，重点关注车辆因作业过程而产生的停留行为，10 min阈值选择可剔除部分外部因素(例如，等待红绿灯和堵车等)造成的干扰。规则2：对于某些跳跃数据记录，某里程记录可能只存在1 条，如果根据规则1，则该里程持续时间为0 min，因此，不会被判断为停留点。对于这部分数据，则计算其前后2条数据记录的里程差以及时间差，得到该时段的平均速度，将平均速度低于某设定阈值的点同样记录为停留点。速度阈值设置与规则1保存一致，选取6 km·h-1。

(2)基于时间阈值的停留点筛选

针对人的出行规律和出行特征已经被大量研究，并且形成了稳定共识，在客运出行的轨迹数据研究中，通常以调查数据或其他多源数据的日均出行次数和出行时长等指标检验时间阈值选取合理性。但货运车辆出行或使用特征的研究基础较为薄弱，并且货运交通类型的多样性和作业方式复杂性，目前，缺少共识性的货车出行切割时间阈值，需要从样本统计量和统计特征稳定性两方面说明出行切割结果的可信度。本文运用抽样统计中的最小样本量原理，针对不同类型重型货车，通过绘制一定数量的车辆时空轨迹图观察每日出行情况，测试对比不同时间阈值选择下的切分结果，选择最符合实际观察结果的时间阈值作为筛选有效停留点的取值。货车单日时空轨迹示例如图3所示。

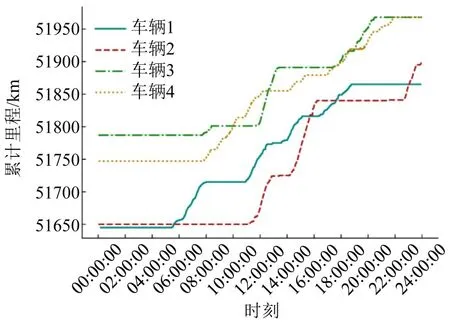
图3 货车单日时空轨迹示例Fig.3 Example of a single-day space-time trajectory of a truck

不同重型货车类型轨迹数据观察的最小样本量确定方法为

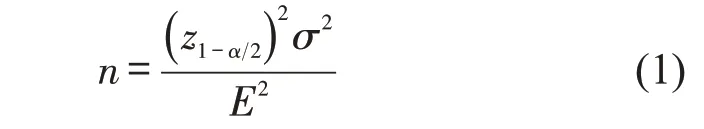
式中：n为最小样本量；z1-α2为95%置信区间下的统计值(1.96)，其中，α为正态分布落在置信区间以外的面积的百分数(0.05)；σ为样本总体标准差；E为可接受误差。

由于总体数据的σ未知，以抽样数据中各类型货车出行次数标准差(σ)作为总体标准差的估计。不同时间阈值选择下标准差有所差异，计算发现，各类货车在不同的时间阈值切割下的σ均小于2.5，因此，选取最大值σ=2.5 确定最小样本量。可接受误差确定为0.5 次，带入式(1)得到计算结果n=97，因此，选取各类货车100辆作为反应总体样本的最小抽样数据。

通过对各类型货车的最小样本量抽样观察和统计发现，集装箱卡车、冷链运输车、土方车、普通大货车及重型罐式车的日均出行次数分别为3.5、4.0、5.0、4.1和7.8次左右。本文设定30，25，30，25，35 min的出行切割阈值，将得到的出行次数与通过最小样本量观察到的出行次数相比较，选择最接近结果的时间切割阈值作为合理结果，得到各类货运车辆轨迹数据的出行切割阈值，如表1所示。可以发现，不同类型的货运车辆合理的出行切割时间阈值是存在差异的，重型罐式车、集装箱卡车和土方车的切割阈值较长，与其单次装卸作业平均时长是紧密关联的。

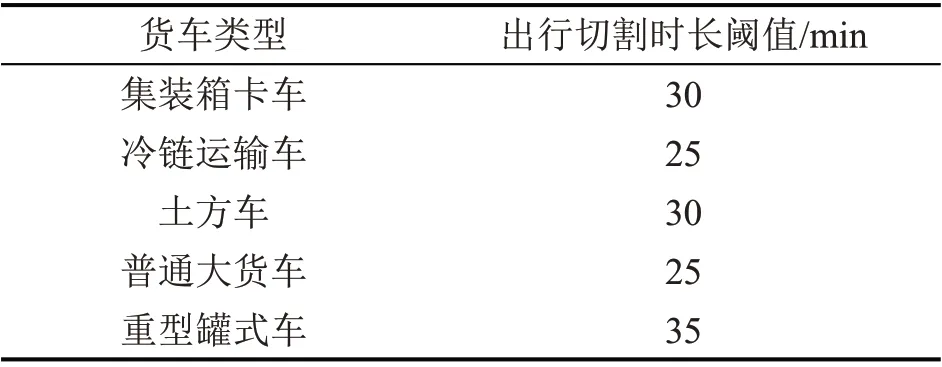
表1 5类货车出行划分时间阈值Table 1 Time thresholds for trips cutting of five types of trucks

1.3 出行界定阈值合理性分析

基于统计抽样的最小样本量方法测试确定不同类型货运车辆出行切割阈值，还需要分析切割结果展现的不同类型货车出行基本特征，以反向佐证方法的合理性。根据确定的出行切割阈值，计算得到各类重型货车基本出行特征如表2所示。

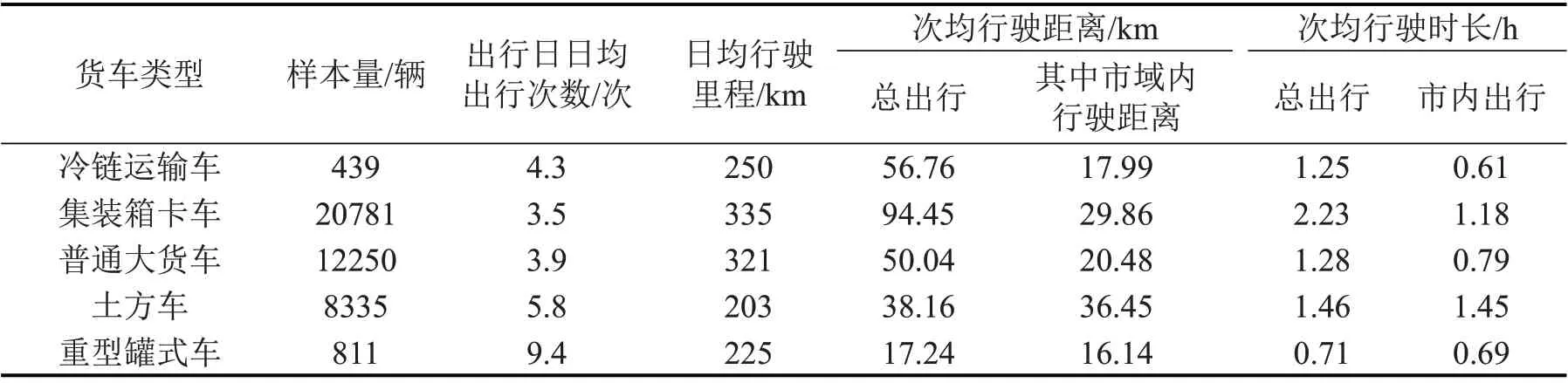
表2 5类货车出行的基本特征Table 2 Basic characteristics of five types of truck travel

由表2 可知，重型货车日均行驶里程基本在200～350 km，远高于客运小汽车30～50 km，表明重型货车的日均使用强度较高；结合日均行驶里程和日均出行次数指标，分析出行界定结果的合理性。载重量越大的货运车辆装卸货时间可能越长，日均出行次数应越少，单次出行距离越长，计算得到的普通大货车和集装箱卡车指标结果符合这一推断。重型罐式车和土方车出行次数显著高于其他重型货运车辆也与其自身作业特点相关，例如，土方车需要频繁往返工地承担“建筑垃圾和建筑材料”运输任务，重型罐式车的装卸方式是独特的。

进一步将结果与既有研究的相关指标交叉验证。YANG等[10]拟合了12 t以上大型货运车辆停留时长的分段幂律分布曲线，发现大于26 min的停留行为才较可能与装卸活动相关，并结合地理信息数据(POI 数据)和路网数据筛选有效停留位置。表2中展示的本文结果与既有研究结果整体是一致的。但不同类型的重型货运车辆活动的关联设施具有显著差异，较难获取可以关联不同类型货车活动的高质量POI 数据支持对各类货车出行数据的构建。本文所采用的方法在结果得到整体合理性检验前提下，可以在缺少完整的POI数据条件下实现不同类型货车出行信息的捕捉和构建，但技术过程更为简洁，具有更好的可移植性。

2 重型货运车辆活动时间差异性

2.1 出车率差异

车辆的出车率体现了用车强度，用1周内的出行天数表征，指1 周内有车辆使用的天数。5 类重型货运车辆的使用天数分布情况如图4所示。

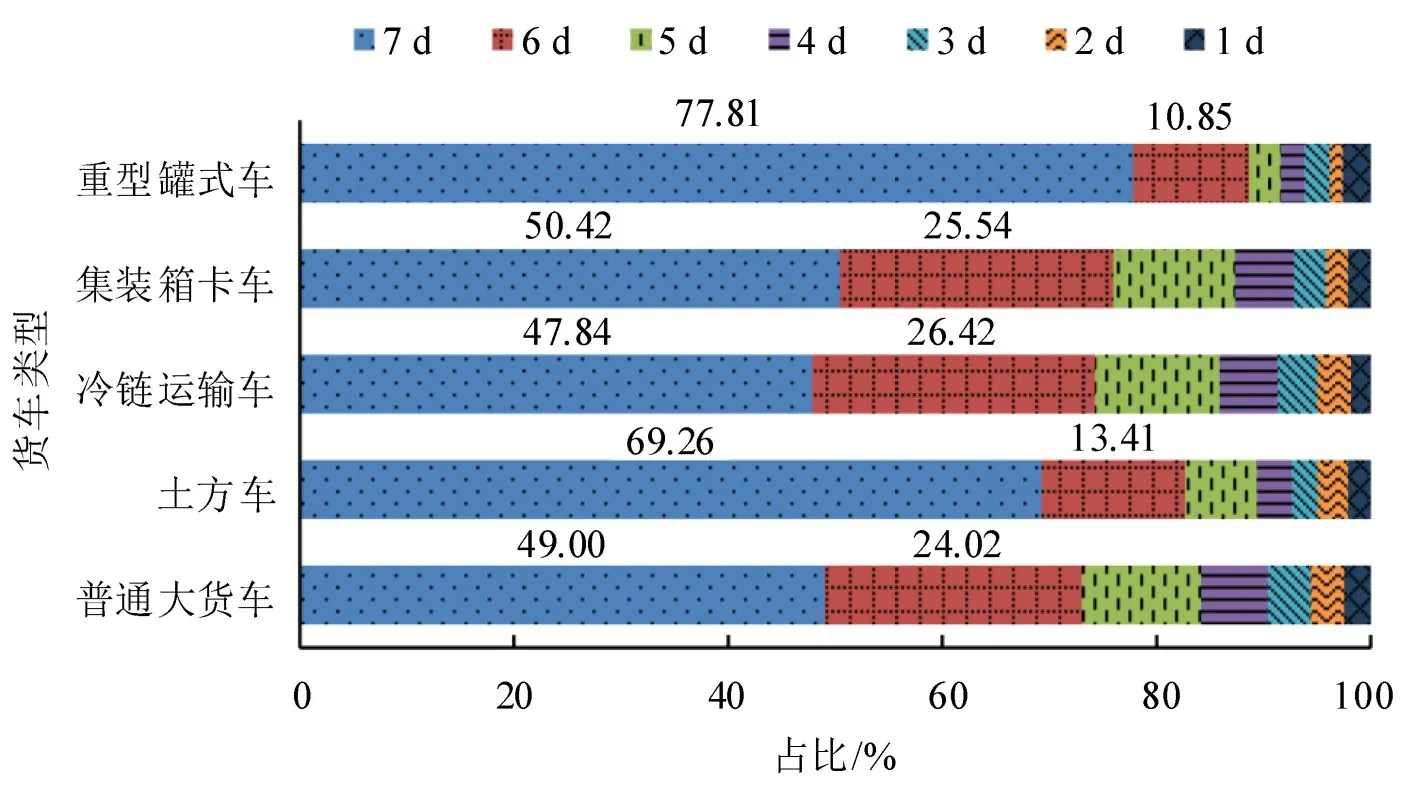
图4 5类货车1周出行天数分布Fig.4 Distribution of number of days with using for five types of trucks

由图4可知，重型罐式车和土方车的出车率明显高于其他类别重型货运车辆，两者1周内每日都出车的比例分别达到70%和67%，其他3 类重型货车仅45%～50%的车辆会在1 周内的每日都会出车。用车强度的不同可能源于货运类型的差异，罐式车和土方车都是专用型作业，车辆规模受管制程度较高，因此，已进入细分市场的车辆利用率较高，其他类型的重型货车市场化程度更高，每日的运输需求受市场调节而存在波动情形。

2.2 出行时段差异

1 d内的出行时段分布是影响重型货车对道路交通网络运行影响的直接因素，例如，是否与小客车具有相同的时段分布等特征。各类货车1 d内所有出行的出发时段的概率密度分布如图5所示，并增加了小客车出行时段分布(基于深圳市个人自用新能源汽车的GPS数据分析结果)对比分析。

图5 5类货车出发时刻分布情况Fig.5 Distribution of trip beginning time for five types of trucks

由图5可知：(1)重型货运车辆出行时段分布密度曲线相比小客车更加平滑，出行波峰-波谷现象不如小客车显著，以集装箱卡车最为典型；但土方车出行有明显的早晚高峰时段，分别为9:00 和20:00，与小客车高峰时段错开，与建筑工地作业计划和土方车交通管理政策紧密相关。(2)货运车辆夜间至凌晨活动较小客车更为频繁，例如，22:00-次日6:00时段占比显著高于小客车，表明重型货运交通有着自身独特的作业计划，对这一特征的深度挖掘是制定高效合理的货运车辆通行管理措施的关键工作。(3)土方车与重型罐式车的夜间出行占比高于其他货运车辆，普通大货车和集装箱卡车更倾向于日间出行，可能与不同类型货运车辆所服务的生产活动要求和交通管制措施的差异是关联的，例如，土方车主要是运输建筑工地挖掘作业的废弃物，而挖掘作业可能存在昼夜连续施工要求，从而带来土方车夜间活动频次较高的特征。

3 重型货运车辆活动空间差异性

货运交通的起讫点与货运设施、货源产生或接收点等紧密关联，可能会带来货运交通在空间上的集聚现象，不同类型重型货车承担的货物类型或用途不同，其集聚特征是否存在差异值得挖掘分析。

3.1 车辆出行的空间尺度

重型货运车辆通常的活动范围并不仅限于单个城市内部，因此，分析货车在城市内部的活动空间特征之前，需要在更大的空间尺度上探索活动空间分布特征。本文的数据对象是注册在深圳(粤B车牌)的12 t以上重型货运车辆，分析重型货运车辆进出深圳市域的活动特征，将货车活动根据起讫点空间位置分为深圳市内活动(市内-市内)、跨深圳市活动(市内(外)-市外(内))以及深圳市外活动(市外-市外)这3 类，5 类货车的3 种活动数量占比如图6所示。

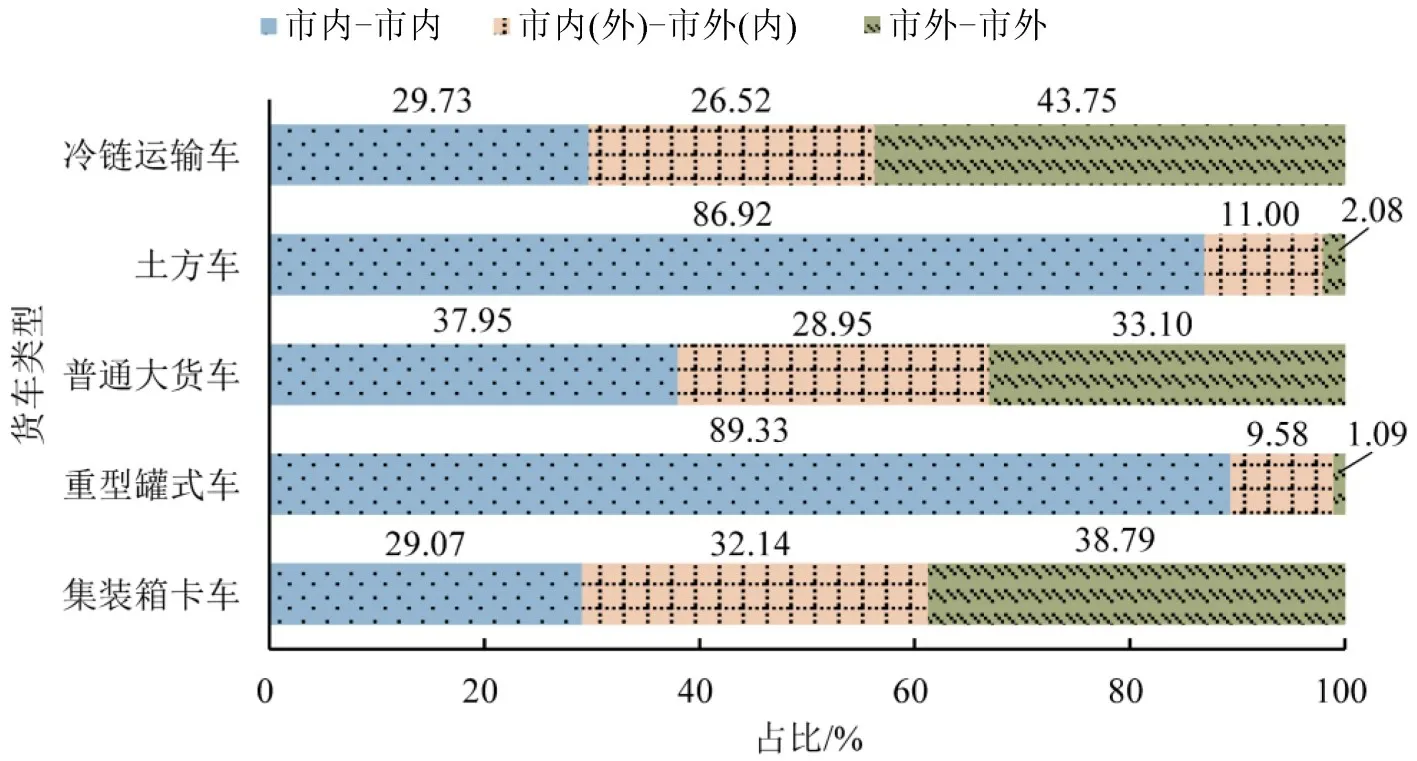
图6 5类货车跨市与市内出行占比Fig.6 Proportion of inner-city and inter-city trips by five types of trucks

由图6可知，土方车与重型罐式车在深圳市内活动占比分别高达87%与89%，说明这2 类车辆几乎完全活动于本地城市，可能与车辆受地区专营制度约束较强是紧密关联的。集装箱卡车的市内活动占比最低，为29.1%，表明集装箱卡车主要承担中长途货物运输服务，其活动空间通常是在区域乃至全国空间中分布。相比之下，普通大货车在深圳市内活动占比接近40%，更主要承担本地运输功能。以街道/镇为空间单元，绘制5 类货车1 周OD的市域空间分布如图7所示。

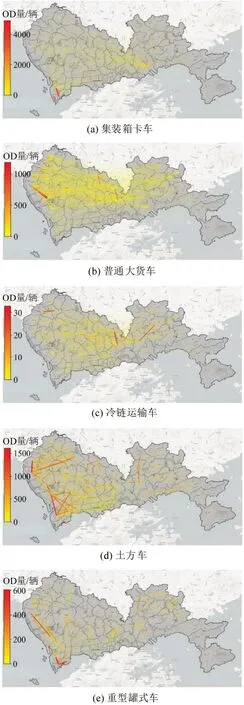
图7 深圳5类货车OD空间分布Fig.7 Spatial distribution of five types of trucks OD in Shenzhen

由图7可知，各类货车出行的空间分布差异显著。集装箱卡车主要与2个海运港口关联，且在港区附近均存在1 个主要货车交通OD 对，与集装箱卡车在港口码头与配套的货运堆场之间的拼箱作业活动相关；普通大货车主要活动在城市外围的工业及仓储区，市内核心区只有极少的重型货车交通，与货车限行和物流分级运输的货运交通政策紧密相关；冷链运输车和重型罐式车的OD空间分布很大程度上能够反映该类货运活动关联特定设施的分布情况；土方车活动区域与城市建设开发活动分布高度相关，从侧面印证了目前深圳市大量开发建设项目集中在城市西部的前海地区以及北部与东莞和惠州一体化发展地区。

3.2 车辆出行的空间集聚

本文通过构建重型货车的出行网络，利用网络节点强度分布刻画重型货车的活动空间集聚特征。以街道或镇为节点，构建重型货车活动网络，以某类货车出行为例，存在1 次从街道i至街道j的出行，则设街道i至街道j为网络节点，记为Vi和Vj，将节点i和j连接，形成有向边Tij，记边Tij的流量权重(边权)wij=1，如果Tij上存在x个OD对，则相应的wij=x。

节点强度代表该街道货车的发生吸引强度，用发生吸引量总和表示，即节点在网络中对流动关系影响的强弱。节点强度分布常采用分布函数或累积分布函数描述，由于实际情形中节点强度分布往往会在其中的一些取值处(特别是尾部的一些地方)有明显的类似于噪声扰动的偏差，绘制累积分布函数曲线能够对此进行光滑化处理。常用的最小二乘拟合方法无法解决幂律分布适用范围与长尾波动的问题，本文基于Kolmogorov-Smirnov(KS)统计量对节点强度分布进行极大似然估计与拟合优度检验[13]。

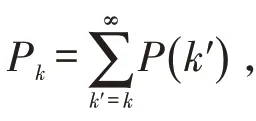
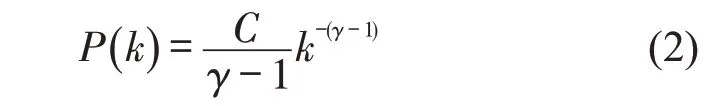
采用极大似然公式估计幂指数为

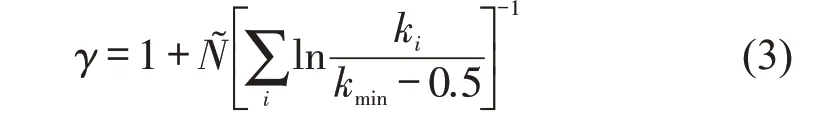
式中：kmin为使幂律成立的节点强度最小值；N͂为强度不小于kmin的节点数，针对所有强度不小于kmin的节点求和。KS统计量为观察数据的累积分布函数与拟合模型之间的最大距离D，S(k)与P(k)分别为观察值与拟合的幂律分布中节点强度大于kmin的累积分布函数，即

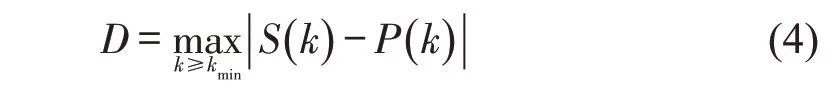
在双对数坐标轴中绘制4 类重型货车出行网络节点强度互补累积分布如图8所示(尾部直线可用于检验是否符合幂律分布，若尾部互补累积分布在双对数坐标轴中趋于直线则满足；冷链运输车活动网络不符合幂律分布，未绘制)，并进行幂律分布拟合，拟合参数如表3 所示，其中，P_value 小于0.05 则拒绝幂律分布。边权分布的差异性可以通过基尼系数衡量[14]。

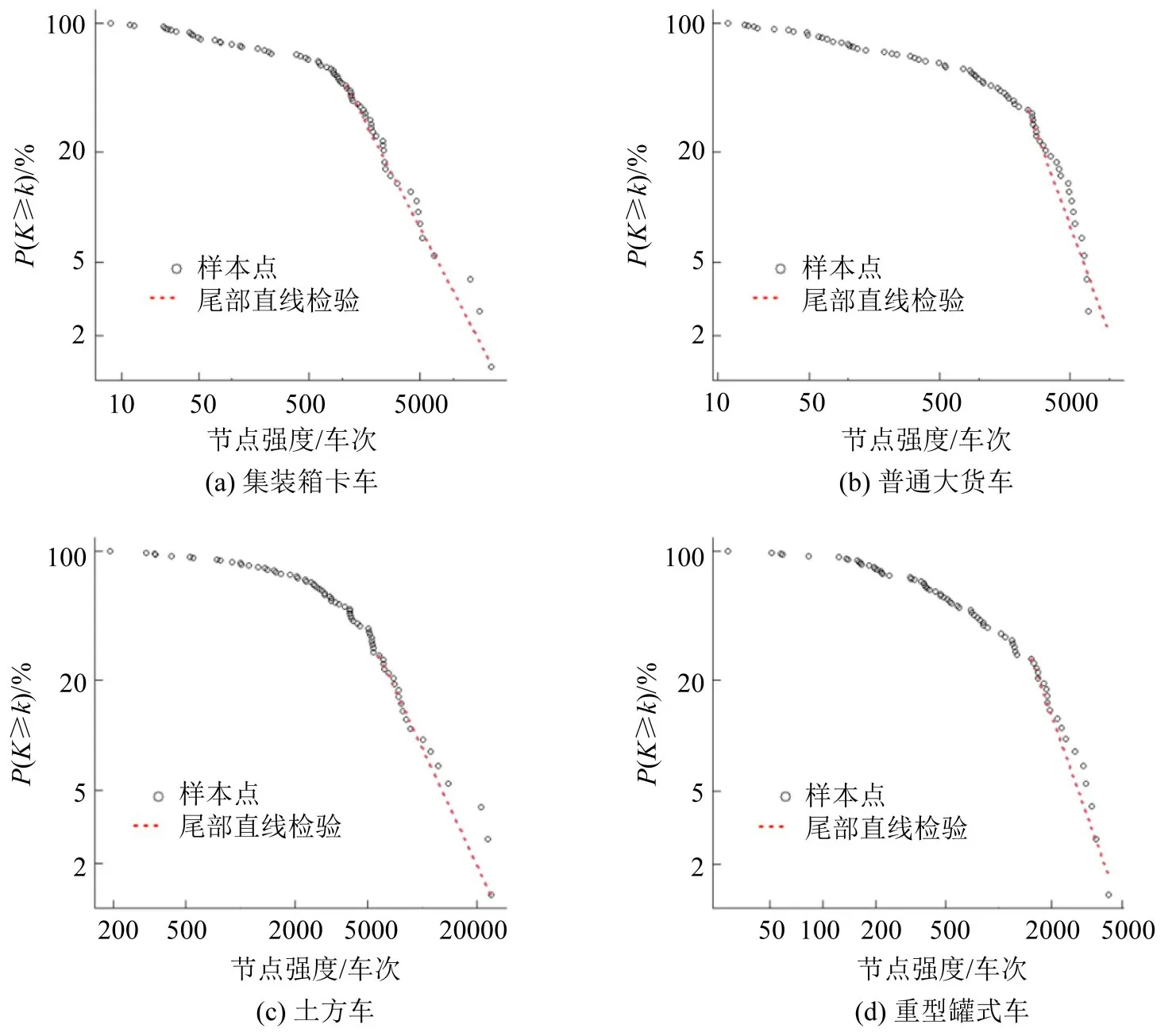
图8 5类货车出行网络节点强度互补累积分布Fig.8 Complementary cumulative distribution of node strength for five types of trucks trip networks

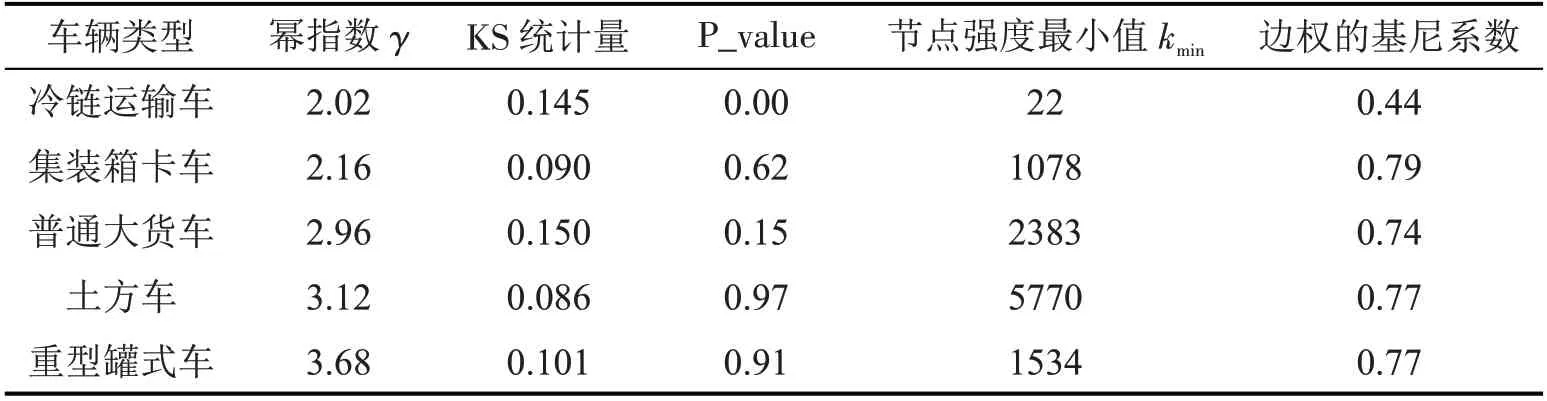
表3 5类货车出行网络幂律分布拟合参数Table 3 Fitting parameters of power-law distribution of five types of trucks trip networks

表3结果显示，除冷链运输车之外(P_value 小于0.05)，其他几类货车出行网络在节点强度大于kmin前提下均服从幂律分布，满足无标度条件，说明货运交通网络具有分级特性，少数空间(本文是以街道/镇为最小空间)聚集了大量重型货车交通量，而大多数街道只有极少数流量。无标度分布的幂指数γ越小，表明，网络节点集中度越高，聚集效应最强的是集装箱卡车，符合实际情况。集装箱卡车更多是连接海港和空港等货运枢纽与大型物流和仓储园区为主，这几类设施在城市空间中数量较少且分布集中。

从边权(节点间流量)基尼系数来看，几类重型货车出行网络同样展现了高度聚集性，边权基尼系数均大于0.5，且大部分在0.7 以上，评价为差距悬殊，集装箱卡车出行网络边权基尼系数是最大的。冷链运输车的节点强度和边权分布较其他重型货车更具有匀质性，这与具有保温运输需求的活动场所(例如，生鲜超市、菜市场及医院等)分布更为广泛和均匀是相关的。

4 重型货运车辆活动空间差异的影响因素

重型货车活动在空间上具有集聚现象，但不同类型车辆的集聚区域是存在差异的，并且与各自货运服务类型是相关的。本文选取样本量最多且具有明显差异的普通大货车与集装箱卡车为对象，探索车辆活动空间差异的影响因素。两类车辆的停留热区如图9所示。

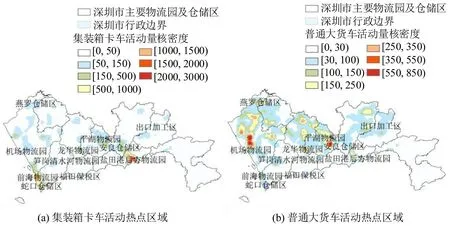
图9 两类货运车辆出行热点区域Fig.9 Two types of freight vehicle trip hotspots

由图9可知，普通货车的活动范围明显广于后者，普通货车主要活动在城市外围区域，与外围工业区以及几大主要物流仓储园区相关联，而集装箱卡车基本集中于城市东西两侧的港口区域内。

本文考虑使用线性模型和非线性模型对比解析两类货车活动空间差异及影响因素。常用的探索非线性影响的模型有广义加性模型(GAM)和广义加性混合模型(GAMM)。相较于多元线性模型(MLR)，GAM 模型和GAMM 模型均能刻画影响因素对响应变量的非线性作用机制，并可以直观解析和量化各影响因素对响应变量的影响[15]。GAM模型和GAMM 模型的基本原理类似，区别在于两者对个体效应的假定不同，GAMM 更适用于长时间周期的面板数据。由于本文以街道及1 周的货车活动量为研究对象，建模数据可以理解为截面数据，因此，选用GAM模型刻画重型货车交通的影响因素及作用。GAM模型由预测变量的平滑函数和组成，即

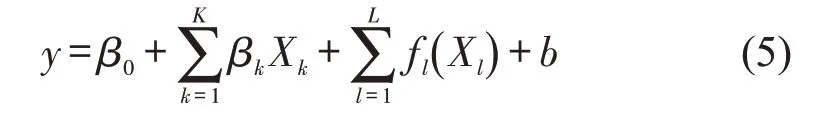
式中：β0为常数项；βk为固定效应Xk的估计参数，K为固定效应Xk的总数；fl为协变量Xl的平滑函数，L为呈现非线性特征的协变量总数；b为随机效应；y为预测变量。

以深圳74个街道的两类货运车辆产生量为研究对象，考虑到影响货运交通产生量的主要因素，选择工业用地建筑面积(BM1)、物流仓储用地建筑面积(BW1)、人口(P)以及街道中心经纬度(Jlon,Jlat)进行建模(经度和纬度常作为GAM 模型的空间因子)，经检验各变量间的方差膨胀因子(VIF)均小于5，满足建模要求。模型拟合参数如表4 所示，影响因素的效应分析如图10 和图11所示。

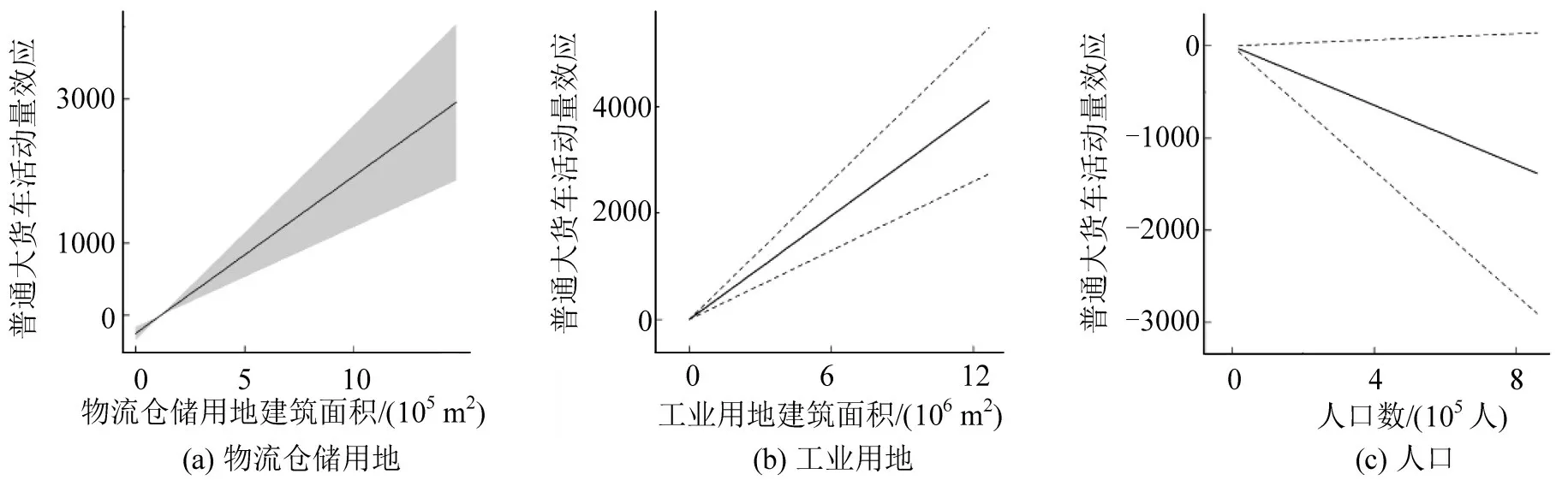
图10 普通大货车活动量与因子间的广义加性模型分析Fig.10 Generalized additive model analysis diagram between ordinary large truck activity volumes and factors

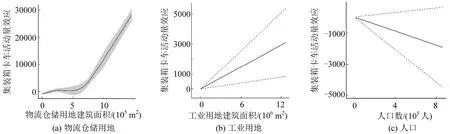
图11 集装箱卡车活动量与因子间的广义加性模型分析Fig.11 Generalized additive model analysis diagram between container truck activity volumes and factors

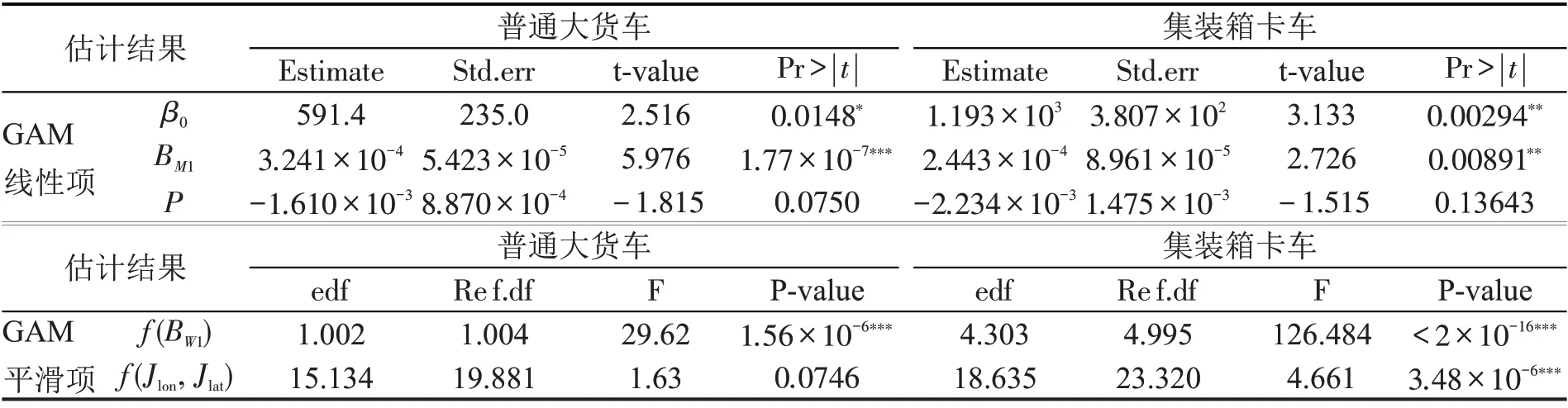
表4 GAM模型拟合参数Table 4 Fitting parameters for GAM model

图10 结果显示，普通大货车交通量与物流仓储用地建筑面积基本保持线性相关性，从工业用地建筑面积对两类货车活动量的影响来看，工业用地对普通货车活动量的影响程度更强，说明普通大货车的活动主要与工业用地紧密相关，但同时也会承担物流园区间的货物运输功能，解释了活动热区中普通大货车主要活动于深圳市外围地区的原因。图11 结果显示，集装箱卡车交通量与物流仓储用地建筑面积之间存在非线性关联，当此类用地规模较小时，曲线增长较为平缓，达到一定规模后增长速率大幅度上升，表明集装箱卡车集中活动于港口以及规模较大的一些特定物流仓储园区，结合活动热区说明，集装箱卡车主要服务于港口货物的集散。此外，图10和图11显示两类货车模型中人口变量均为非显著变量，且与货运交通量成负相关关系，也佐证了大型货运车辆的活动区域集中分布于人口相对稀疏的城市外围大型物流仓储园区和工业园区等空间，较少参与人口密集的城市内部货运。

为验证广义加性模型(GAM)的解释能力优势，本文同步应用了多元线性模型(Multiple Linear Regression,MLR)进行对比。根据上述4 个变量建立多元线性回归模型，通过AIC 值对比GAM 模型与MLR模型性能差异，如表5所示。

表5 GAM模型与MLR模型性能比较Table 5 Performance comparison of GAM model and MLR model

由表5 可以发现，GAM 模型效果均优于MLR模型，但对于集装箱卡车而言，GAM模型提升效果更为显著，体现了GAM 模型在拟合非线性作用机理方面的优越性。

5 结论

本文基于深圳注册的12 t 以上重型货运车辆GPS轨迹数据，提出了出行切割时间阈值的确定方法，重点刻画了不同类型重型货运车辆的活动时-空特征差异性，分析了集装箱卡车和普通大货车活动空间分析的影响因素，主要结论如下：

(1)针对重型货运车辆的轨迹数据处理，需要结合不同类型车辆的运输功能和作业特征，差别化确定轨迹数据切割出行的时间阈值。本文提出，在尝试不同的切割阈值条件下，基于可接受误差水平下的最小样本量确定适当的时间阈值水平。基于深圳的重型货车数据，出行切割的时间阈值整体在30 min左右更合适。

(2)车辆活动的时间特征方面，土方车与重型罐式车使用强度明显高于其他3 类，除土方车以外，重型货车出行时段分布曲线较小客车平缓得多，出发时刻较为分散。重型货运车辆在夜间及凌晨时段(22:00-次日6:00)出行比例相比小客车而言占比更高；普通大货车则主要集中在9:00-15:00 之间，土方车展现了明显的日间早晚波峰，但与小客车的早晚高峰存在一定的错峰现象。重型货运车辆活动的时间特征结果显示，大部分类型货车出行与小客车出行高峰并不完全重叠，这种特征是货运车辆通行管理措施和货运行业运作机制的双重作用结果。

(3)车辆活动的空间特征方面，土方车和重型罐式车这2 类货车主要活动于本地，其他3 类车辆均存在频繁的跨城市活动。除冷链运输车之外，重型货运车辆均存在明显的空间聚集现象，在以街道镇为节点的活动网络中，节点强度在一定条件下服从幂律分布，表明货运交通具有分级特性，少量空间聚集了大部分的货运交通量。其中，集装箱卡车的活动空间最为集中，与港口和大型物流设施的分布密切关联，此外，集装箱卡车活动量因其空间上的高度集中而体现出与物流仓储用地规模的非线性关系，大规模的设施能够集聚更大比例的集装箱车辆交通量；普通大货车活动还与工业园区和工业用地有紧密关联，其活动量与工业用地及物流仓储用地规模呈现出稳定的线性正相关关系。

总结而言，本文提出的轨迹数据的出行切割阈值确定方法能更好体现不同类型货车的作业特征。对重型货运车辆活动时-空间特征的分析和基于广义加性模型(GAM)的影响因素识别，是深入理解货运交通运行规律及差异性的基础工作，对编制货运交通发展战略和规划，构建货运交通需求模型等实际工作有重要的支持作用。