重夸克势能模型中非微扰贡献重要性的定量研究

唐爱琪，杨 航，孙亚男

（广西师范大学物理科学与技术学院，广西 桂林 541004）

1 引言

近数十年，物理学家们一直都在寻找脱离禁闭状态的夸克胶子物质，但夸克胶子物质存在需要非常严苛的条件，例如要在体系的温度或者重子数密度要非常的高才可以存在。在地球，我们可能达到严苛条件的可能只有相对论重离子碰撞试验。在进行重离子碰撞时，会产生处于热平衡的物质称它为“夸克-胶子等离子体”(QGP)，即QGP 产生于碰撞初期。又因为，体系本身会发生膨胀，而导致体系的温度下降，因此QGP 会因温度的降低而演化为强子气体冻出，从而导致我们最终探测器探测到的都是末态的强子，即我们是无法直接观测到QGP 的！在重离子碰撞试验中，我们无法之间观测到夸克胶子等离子体，我们观察到的是末态的强子气体。在实验上就只能去分析这些末态的粒子，当然也需要依靠可靠的理论数据计算。对碰撞早期物质状态敏感的末态粒子称为“QGP 的探针”。[1]本文我们重点利用的探针为：重夸克偶素。由于“重夸克偶素”的质量比较大，相对论效应比较弱，所以，通过非相对论下的薛定谔方程，我们可以很好的去研究“重夸克偶素”性质，通过求解薛定谔方程，我们可以得到“重夸克偶素”的束缚能和本征能。因此，构建出能够很好描述“重夸克偶素”性质的重夸克势能模型对研究重夸克偶素的物理性质是非常重要的。本文将利用由Karsch，Mehr 和Satz 等人引入、郭云教授改进的的重夸克势能模型（以下简称“改进拓展的KMS 重夸克势能模型”）为代表，来进行重夸克势能模型中非微扰贡献重要性的定量研究。

2 改进拓展的KMS 重夸克势能模型简述

2.1 原始KMS 重夸克势能模型推导及介绍

由于组成重夸克偶素的夸克的质量较大，相对运动速度比较小，因此，当粗暴的假设夸克与反夸克之间的相互作用力是一个简单的静态势时，就可以应用非相对论来近似。

第一个著名的势模型是Cornell 势：

其中，αs是强相互作用的耦合常数，σ是弦强度，r 是夸克与反夸克之间的距离。零温度下的Cornell势由微扰部分和非微扰部分的唯象模型σr两部分构成。1988 年，由F.Karsch,M.T.Mehr 和H.Satz 开创性的模仿零温度下Cornell 势，引入了有限温度下的简单的势能模型，称为原始的KMS 重夸克势能模型。

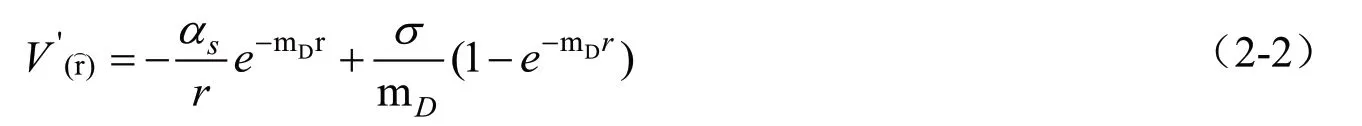
其中德拜质量mD是与温度有关的函数，我们可以看到在有限的温度下，势能（2-2）式表示的重夸克势能为指数的形式。且通过与格点数据进行对比，Karsch 等发现，原始的KMS 重夸克势能模型是能够与格点数据中的自由能数据拟合良好。

当德拜质量mD→0时，则有

我们发现。此时的势能公式与零温度时的Conell 式的形式一模一样！

2.2 改进拓展的KARSCH-MEHR-SATZ 重夸克势能模型的介绍与探索

在2007 年，M.Laine 等人首次提出重夸克势能模型有虚部并将有限温度下的重夸克势能模型表示成复值的形式后，KMS 重夸克势能模型也在不断的发展、变化。实际上，2.1 中提到的（2-2）式就是原始的KMS重夸克势能模型，它可以去定性的描述格点数据，但引起物理学家思考的是：重夸克偶素的质量并不都是足够大的，如粲夸克偶素或底夸克偶素，它们在非相对论的极限下并不能使用微扰势能去描述其间的相互作用，所以，一个包含非微扰项的势能形式脱颖而出了。为描述非微扰的影响，2019 年，郭云教授等借助E.Megias等人提及的二维胶子凝聚的贡献，尝试提出解决的方法：在微扰（延迟）胶子传播子中加入了一个新的唯象式。[错误!未定义书签。]通过傅里叶变换即可得到扩展的KMS 重夸克势能模型的实部具体形式如下：

同理，扩展的KMS 重夸克势能模型虚部具体形式如下：

其中:

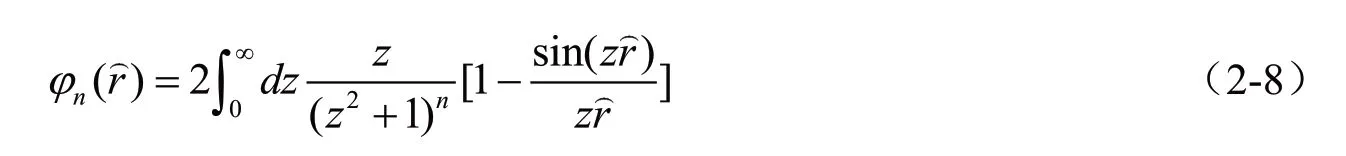
即VKMS=ReV+iImV，为扩展的KMS 势能模型。

那么扩展的KMS 势能模型得到的数据能否在格点数据范围内呢？2017 年，Y.Burnier 和A.Rothkopf 发表了拥有淬火QCD 格点数据的文章，与扩展的KMS 势能模型拟合情况如图1、图2：

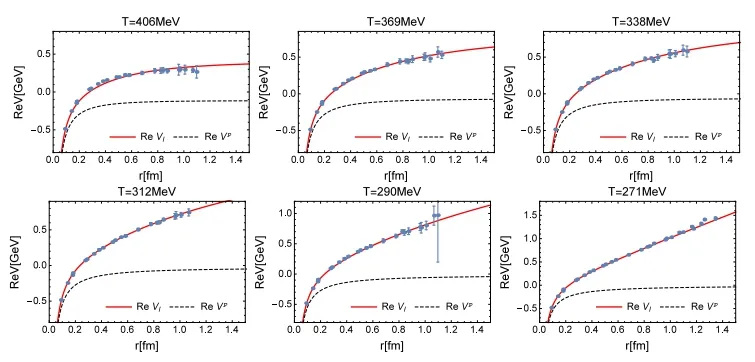
图1 淬火QCD格点数据（蓝点）和扩展KMS势能模型中的实部ReV的比较，其中，ReV由红实曲线表示，只考虑微扰贡献的由黑虚曲线表示。[1]

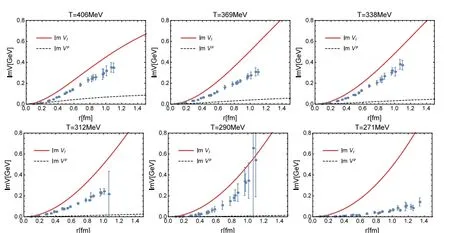
图2 淬火QCD格点数据（蓝点）和扩展KMS势能模型中的实部ImV的比较，其中，ImV由红实曲线表示，只考虑微扰贡献的由黑虚曲线表示。[2]

通过图1 和图2 可以发现：扩展KMS 重夸克势能模型的实部部分与格点数据拟合的很好，且当距离较大时的行为明显是夸克禁闭的行为；但扩展KMS 重夸克势能模型的虚部部分在随着r 的增大，发生集聚增大的变化并超过了格点数据。虽扩展的KMS 模型虚部拟合效果不如人意，但仍比只考虑微扰贡献有了明显进步，这也提醒我们，目前扩展的KMS 势能模型，特别是虚部部分仍然需要进行进一步的改进。

幸运的是，在对扩展的KMS 重夸克势能模型与淬火QCD 格点数据拟合情况并不满意后，为了更好的符合格点数据的虚部部分，郭云教授等继续又对扩展的KMS 重夸克势能模型进行了再一次的改进，改进思路在非微扰项中在二维胶子传播子中继续加入新的贡献，并同样再进行傅里叶变换，即可得到改进拓展KMS重夸克势能模型。

具体形式如下：

同理，改进扩展的KMS 重夸克势能的虚部具体形式如下：

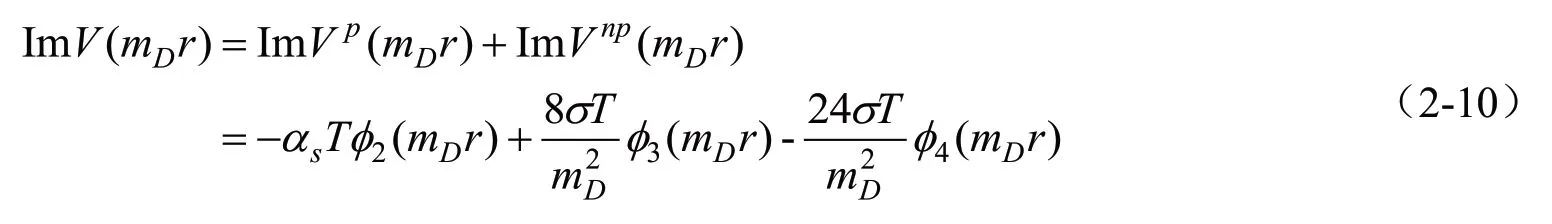
其中:

又，考虑到夸克的质量mQ有限，为提高解得的夸克态波函数的精度，选择加入一个与成比例而与自旋无关的一个修正值。即，为改进扩展的KMS 重夸克势能模型最终形式，如（2-12）式。同样与淬火QCD 格点数据进行对比，发现在实部拟合依然很好的情况下，虚部部分的拟合也有了很大的改进[2]。

现在，我们通过将（2-9）式带入薛定谔方程，即可求出重夸克偶素的本征能，我们将利用mathmatica程序，对改进拓展的KMS 重夸克势能模型带入薛定谔方程进行计算以获得重夸克偶素的本征值。

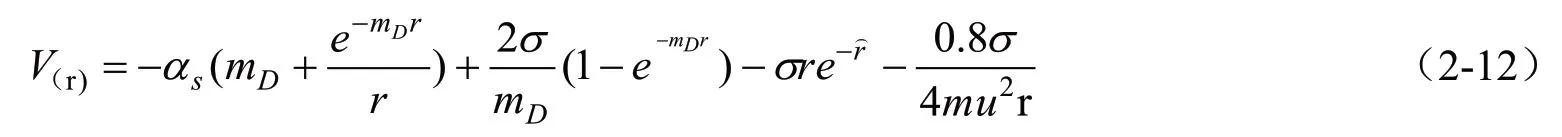
我们可以看到（2-12）式包含微扰项和非微扰项，为了去探索改进拓展的KMS 重夸克势能模型中非微扰贡献重要性，我们选择将σ=0时的改进拓展的KMS 重夸克势能模型，如（2-13）式，并同样利用mathmatica程序将其带入薛定谔方程以获得无非微扰时重夸克偶素的本征值。

当σ=0时，

通过改重变温度和夸克偶素的质量可以得到两种情况下对应不同温度、不同质量的相应本征能。通过的两种情况对比，我们可以得到，当重夸克偶素的质量达到多少时，非微扰不再影响本征能的值，达到定量研究改进拓展的KMS 重夸克势能模型中非微扰贡献重要性的目的

3 实验结果

我们利用mathmatic程序，对改进拓展的KMS重夸克势能模型进行计算，并计算了多种温度下不同质量的下的本征能，利用数据所画图像如图3所示。

图3 黑色曲线为温度0.192*1.1GeV时，其中黑色虚线代表σ=0时本征能随质量的变化，黑色实线代表σ=0.215时本征能随质量的变化；红色曲线为温度0.192*5.0GeV时，其中红色虚线曲线代表σ=0时本征能随质量的变化，红色实线代表σ=0.215时本征能随质量的变化；蓝色曲线为温度0.192*10.0GeV时，其中蓝色虚线代表σ=0时本征能随质量的变化，蓝色实线代表σ=0.215时本征能随质量的变化。

4 结论

通过图3 的横向的对比，我们发现在同一温度下，随着重夸克质量的升高非微扰部分对通过重夸克势能模型得到的本征能的影响逐渐降低，当重夸克质量一定程度时(如温度为0.192*1.1GeV，重夸克质量为50GeV 时），非微扰部分基本不能再影响本征能的值。

即，我们可以得到结论：当重夸克质量一定程度时(如温度为0.192*1.1GeV，重夸克质量为50GeV 时），非微扰部分不能再影响重夸克本征能的值。

而我们知道，实际上，像b夸克偶素态这样的最大的夸克质量也仅为4.7GeV，显然在现实中，重夸克势能模型中的非微扰贡献是非常重要、不能被忽略的！