颗粒沉降效应的探究

杨彦辉，韩舒婷，冯洁

(1.青岛大学材料科学与工程学院，山东 青岛 266000；2.青岛大学物理科学学院，山东 青岛 266000)

1 引言

沉淀物的沉降分离是化工生产中的重要环节，沉降时间的大小关系着生产的效率。然而，对于沉淀物颗粒分别为低浓度和高浓度的情况下是否遵循相同的沉降规律还有待实验研究。特别地，在高浓度情形下，已报导的相关的研究需要计算机进行计算[1]。本文对极低和极高浓度(颗粒体积约占容器总体积的1/5)两种极端情况进行研究，应用Stokes公式、密舍尔斯基方程等理论进行建模，利用得到的实验数据对模型进行修正，最终给出与实验结果符合得较好的公式。

2 模型建立与理论分析

通过预实验发现：低浓度颗粒沉降和高浓度颗粒沉降遵循不同的运动规律。容器倾角越大，低浓度颗粒沉降所用时间越长；高浓度颗粒沉降反之。基于此，对两种不同的模型分别进行理论分析。

2.1 低浓度颗粒沉降

本文约定，颗粒都是半径为r、质量均匀的球体，盛有液体和颗粒的容器是半径为R的圆柱筒，厚度忽略不计，容器与水平面的夹角为θ(0<θ<π/2)。

当颗粒的浓度(单位体积颗粒数)较小时，颗粒间的距离较大，颗粒的运动互不影响。选择一个颗粒作为研究对象，研究其运动情况，推广到整体。图1中Ox，Oy，Oz是三个两两正交的坐标轴，Oxz平面表示过容器轴线的平面，Oy延容器底面直径指向纸面内。为了简化分析，只考虑颗粒初始位置在xz平面附近的情况。颗粒沉降过程分为两个阶段。图（a）阶段一（时间为0～t1）：在重力G、浮力f和粘滞力F作用下，颗粒从初始位置(x0，y0，z0)处以初速度v0=0竖直下落，直至触壁到达(x1，y1，z1)；图（b）阶段二（时间为t1～t2）：在重力G、浮力f、粘滞力F、与管壁的摩擦力Ff、支持力FN作用下，颗粒从位置(x1，y1，z1)处沿管壁做直线运动，最后落到试管底部。

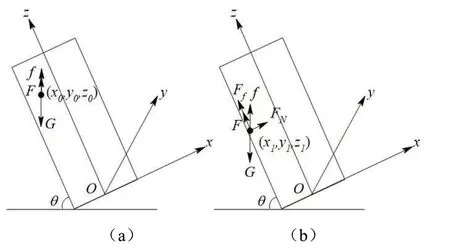
图1 理论分析图

基于Stokes公式[2]，颗粒在运动过程中受到的粘滞力：F=6πηrv.

2.1.1 阶段一

由解析几何的知识求得阶段一竖直下落高度H

竖直下落过程中，颗粒在重力G、浮力f和粘滞力F作用下运动的微分方程为

（3）式满足的初值条件为

其中，ρ为颗粒密度，ρ0为液体密度，g为重力加速度，v为颗粒速度。

由（3）、（4）式求解，得

用（5）式对时间积分求得竖直下落高度H与阶段一竖直下落时间t1的关系

当t1不太小时，（6）式可简化为

所以

基于（2）、（8）式，得出竖直下落所需的时间t1。

2.1.2 阶段二

颗粒在与容器壁相碰后沿切面法向的速度瞬间变为0，即只有沿切面向下的速度，颗粒将沿器壁斜面做直线运动，直至落到底部。

由解析几何的知识求得阶段二碰撞点到底部的距离即沿壁下滑的距离L

沿壁下滑过程中，颗粒在重力G、浮力f、粘滞力F、支持力FN的作用下运动的微分方程为

(10)式满足的初值条件为

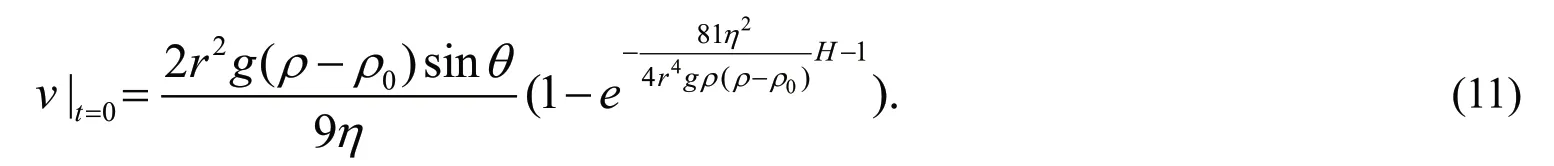
其中，ρ为颗粒密度，ρ0为液体密度，g为重力加速度，v为颗粒速度。

由（10）、（11）式求解，得

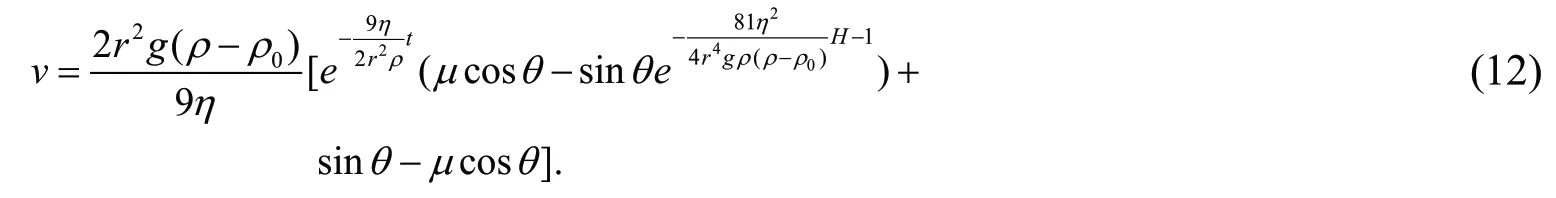
用（12）式对时间积分求得沿壁下滑距离L与阶段二沿壁运动时间t2的关系

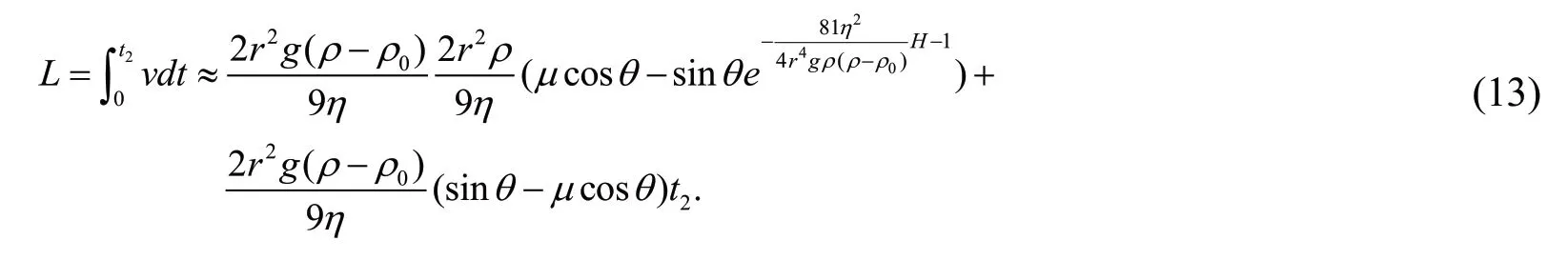
所以

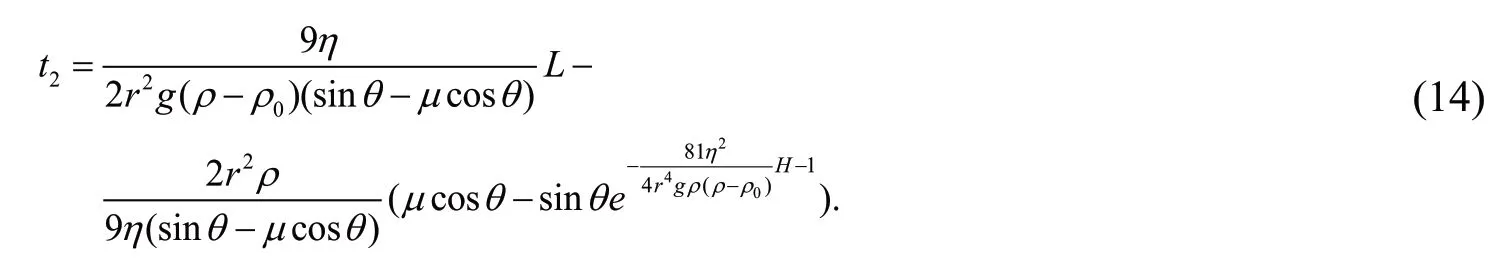
基于（9）、（14）式，得出沿壁下滑所需的时间t2。

整个沉降过程所用时间t

由（2）、（8）、（9）、（14）、（15）式求得

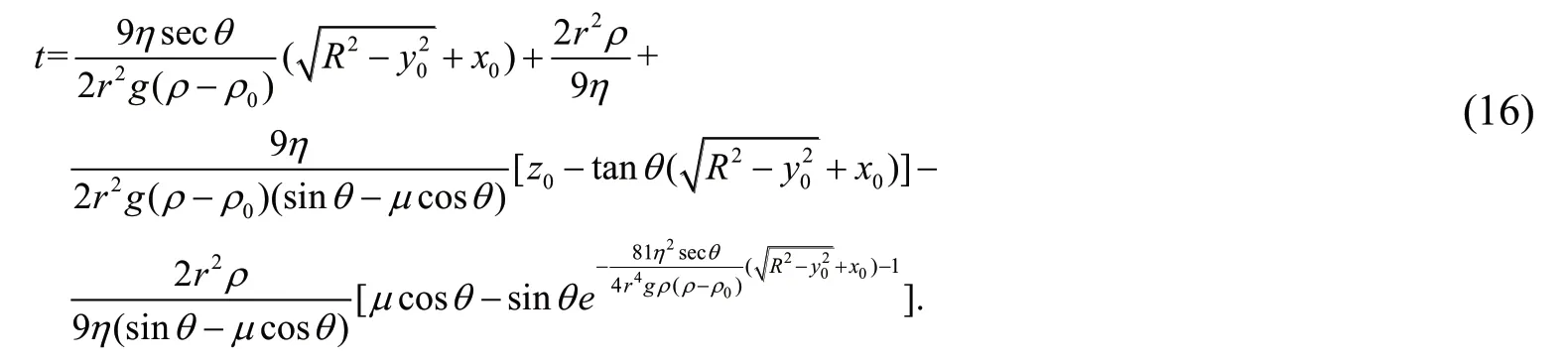
2.2 高浓度情形

当颗粒浓度较大时，颗粒间的相互作用不可忽略。将所有颗粒组成的整体看作连续介质，而每一个小颗粒类比为介质中运动着的粒子，对颗粒整体进行分析。

如图2，在完整的运动过程中，颗粒整体的上表面始终与试管底面平行，且未沉降到底面的颗粒始终均匀分布。流体的黏度较小时，流体黏性对颗粒运动的影响远小于颗粒间相互碰撞的影响和颗粒与管壁摩擦的影响，故可以忽略。

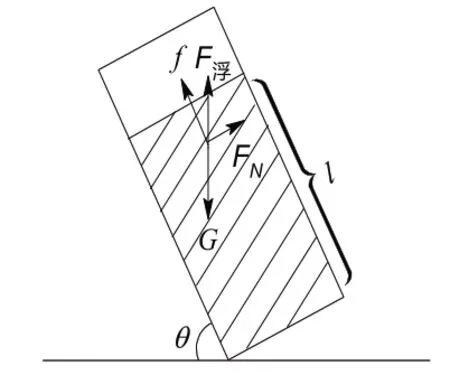
图2 高浓度情形示意图

本文约定，初始状态时颗粒整体的上表面到试管底面的距离为L，沉降到底面的颗粒体积为0（即不在底面堆积），任意时刻到底面的距离为l，颗粒整体质心速度为0，其他条件与低浓度时相同。

将颗粒的沉降视为一个变质量动力学问题，由密舍尔斯基方程[3]可得

其中，MV是颗粒整体的总动量，N是底面作用于颗粒整体上的力，F1是作用于颗粒整体的其它力的合力沿容器壁母线方向的分力。当颗粒质量较小且运动速度不大时底面对颗粒整体施加的反作用力N近似为0，故方程可简化为

（18）式满足的初值条件为

这是一个二阶非线性常微分方程，可以通过换元法求解，求解得沉降时间为

3 实验探究与公式修正

3.1 低浓度颗粒沉降

3.1.1 实验仪器

半径0.5mm的金属小球、蓖麻油、变温黏滞系数实验仪、PID温控实验仪、phyphox软件。

图3 实验仪器

图4 实验操作图

3.1.2 实验分析

在低浓度颗粒沉降中，只需研究其中一个颗粒即可推广到整体。为方便控制变量，采用单粒金属小球在蓖麻油中的沉降实验，探究低浓度颗粒的沉降时间与倾角和温度的关系，并对公式进行修正。

由式（16），需要用到的数据有：蓖麻油粘滞系数η和密度ρ0，变温粘滞系数实验仪与水平面的夹角θ，变温粘滞系数实验仪容器内径R，小球半径r和密度ρ以及初始沉降位置(x0，y0，z0)，小球和管壁间的摩擦系数μ。其中，ρ0、ρ、θ、x0、y0、z0、R、r可直接获得，不同温度下的η值可从文献中查得[4]，μ需采用实验测量。

3.1.3 实验步骤

（1）小球与管壁间摩擦系数μ的测量：使变温粘滞系数实验仪试管水平放置，将金属小球放置在玻璃管口，确保小球不会滑落。缓慢抬起实验仪，待小球刚开始滑落的瞬间停止。用phyphox软件读出此时试管与水平面的夹角θ0，利用公式：

求出小球与管壁间的摩擦系数。

（2）测量不同温度不同倾角下小球沉降时间：在玻璃管中倒入蓖麻油，液面与0刻度线相齐。打开控温装置，设置所需温度，待温度稳定十分钟后，将玻璃管倾斜一定的角度，将半径0.5mm的金属小球从液面中心无初速度下放。下放的瞬间开始计时，待小球落到管底后停止计时。改变倾角，其他条件不变，按相同方法测量小球下落所需时间。升高温度，在不同的温度下再按以上步骤测量下落时间。

3.1.4 实验数据与分析

R=0.01m，r=0.0005m，ρ=7，86*103kg/m3，ρ0=0.95*103kg/m3，g=9。8kg*m/s2，η从文献中查得[4]，由式（21）式求得μ=0.582，下落初始位置的坐标为(0，0，0.382)。将各参数代入（16）式，计算结果如下：

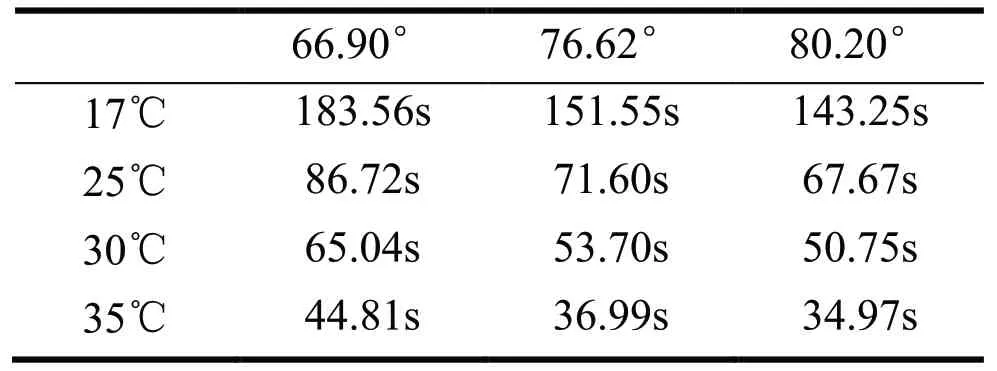
表1 理论数据

通过实验获得的数据如下：

表2 实验数据

对比实验数据和理论计算值可以发现，二者偏差较大，但随着倾角增大，沉降时间的变化趋势相同。

分析主要原因，小球在管壁上滑动时受到的粘滞力偏离Stokes公式，用t实验与t理论作比，除去可疑值后对所得数据取平均，得到表3所示结果：

表3 实验与理论的偏差

3.1.5 模型修正

由表3，在同一温度下，随倾角的变化，理论值与实验值的比值近似为一个常数。计算表明，t理论主要取决于（16）式中的第二项，即

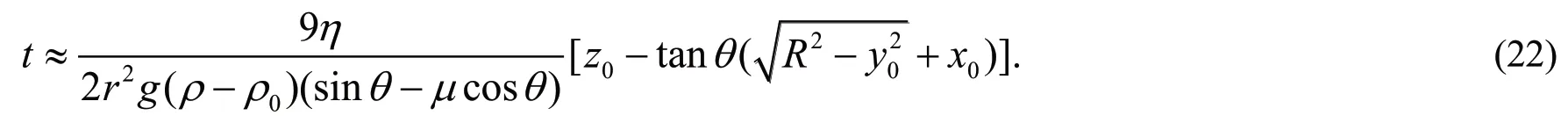
因此，将上式乘上一个与倾角无关的修正系数k则可以得到与实验较符合的结果。

3.2 高浓度颗粒沉降

3.2.1 实验仪器

不同高度的35mm口径的试管、细沙、清水、分样筛、量筒、烧杯、分析天平、背景板

3.2.2 实验分析

由式（20），需要用到的数据有：水的密度ρ0，沙粒的平均密度ρ，试管与水平面的夹角θ，沙粒和管壁间的摩擦系数μ，颗粒整体的上表面到试管底面的距离即试管长度L。其中，ρ0、θ、L可直接获得，ρ、μ需采用实验测量。

3.2.3 实验步骤

（1）沙粒密度的测定：用分样筛对原始沙样品进行筛分，取45目到60目之间的沙粒进行实验。将沙粒样本进行烘干，用干燥容器盛放，准备一个烘干的烧杯。调节好分析天平，放入烧杯，去皮，然后将沙粒样本倒入烧杯中进行称量，读数为x克，然后将烧杯取出，关闭分析天平。准备一精确度较高的量筒，倒入适量的水，读数为n毫升。将烧杯中的沙粒全部倒入量筒中，读数为m毫升。计算沙粒密度为x/(m-n)克每立方厘米。

（2）摩擦系数的测定：将样本试管洗净并烘干。将试管水平放置，并在起靠近试管口出放置少量沙粒。保持试管底部不动，并缓慢抬起试管口，当发现试管内的沙粒刚滑下时停止移动试管，并记录此时的试管与水平方向的夹角θ0。重复上述实验，记录三次实验数据并取平均值。按照公式(21)计算摩擦系数。

图5 实验操作图

（3）沉降时间的测定：将一定量的细沙倒入试管中，注满清水，用软木塞塞紧瓶口，先倒置试管使沙粒充满试管顶部并适当摇晃使沙粒间紧密接触。迅速旋转试管使其竖直（试管口朝上），等待沙粒下降，待沙粒整体的上表面快要脱离试管顶部时将试管旋转至所需的角度，此时沙粒正好完全脱离试管顶部下沉，开始计时。该操作可以使沙粒整体的质心速度近似为0。等到几乎所有沙粒都沉降到试管底部（此时沙粒整体的上表面与桌面间的距离不发生明显变化）时停止计时。其他条件不变，改变倾斜角度，分别测定60°、65°、70°、75°、80°、85°、90°时沉降的时间。适当改变沙子用量，换用不同高度的试管，在其他条件不变的情况下，继续测定这些角度对应的沉降时间。实验现象用相机拍摄记录。

3.2.4 实验数据与分析

ρ=2.69*103kg/m3，ρ0=1.00*103kg/m3，μ=1.676，g=9.8kg*m/s2，将各参数代入（20）式，计算结果如下：

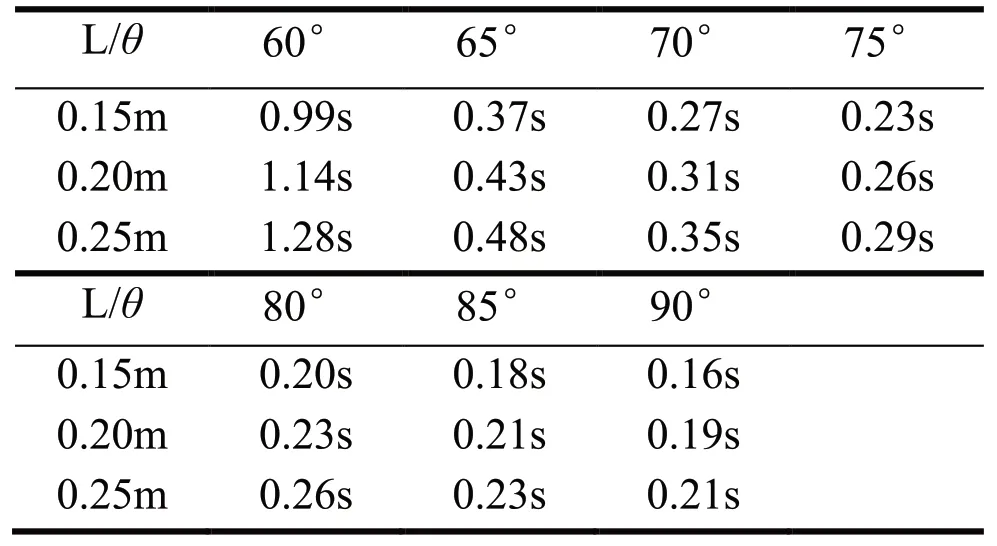
表4 理论数据

通过实验获得的数据如下：

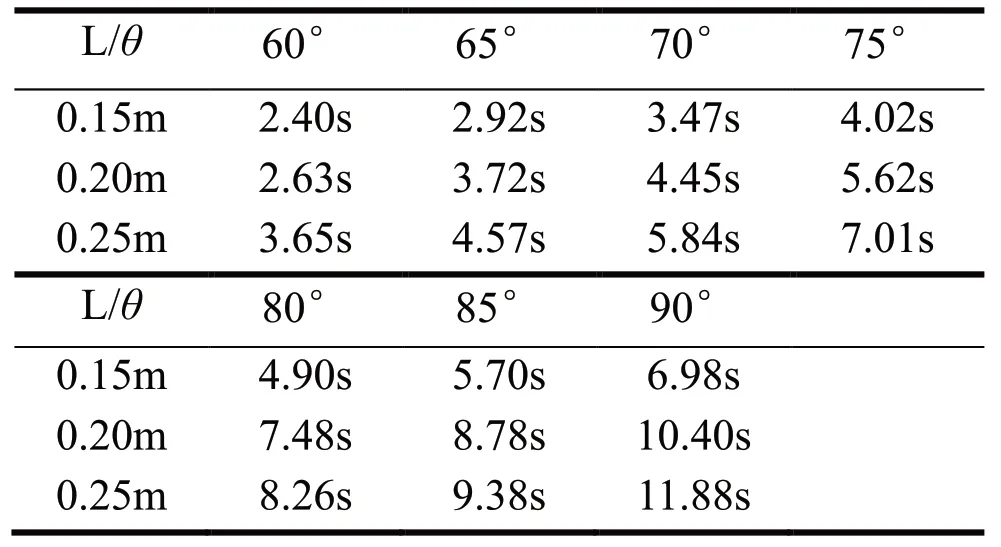
表5 实验数据

对比实验数据和理论计算值可以发现，二者同样差别较大，原因主要是：

(1) 未充分考虑流体的运动对颗粒的影响；

(2) 颗粒沉降到试管底部后会堆积在试管底部，其体积不可忽略；

(3) 由于实验的操作方法，不能保证颗粒整体的质心初速度每次都为0；

(4) 颗粒在沉降过程中不能总是达到均匀分布。

故需要对公式进行修正。考虑到流体运动的复杂性，难以从机理上得到精确的公式，只能在原公式基础上进行修正。通过观察实验数据发现，数据近似成线性关系，因此猜想修正的表达式为

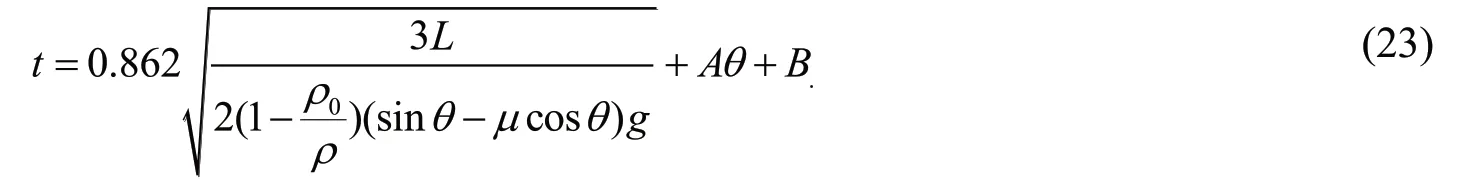
其中A，B为经验参数，且与θ无关。

以t-0.862*sqrt(3*L/(2*(1-r0/r)*(sinθ-μ*cosθ)*g)对θ作图，得到图6的拟合图像。

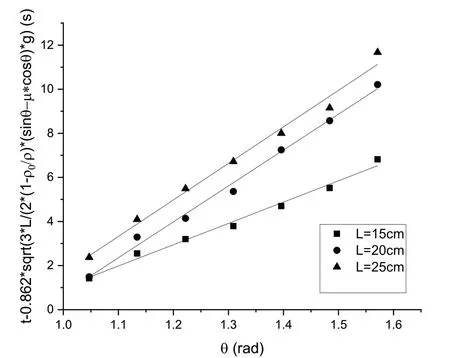
图6 数据拟合图

从上到下拟合得到的三条直线的相关系数的平方分别为r1=0.9940，r2=0.9966，r3=0.9941，修正后的公式与实验结果符合得较好。

4 总结与讨论

在低浓度实验中，当玻璃管倾斜放置时，小球很快落在管壁上，而后沿管壁下滑，沉降时间明显较竖直放置时长。在其他条件不变的前提下，随倾角的增大，小球落到管底的时间越短。可做如下解释：如图7所示，小球沿斜面向下运动时，随倾角的增大，小球获得的沿斜面向下的加速度也增大。由于小球下落的总时间取决于其在管壁上运动的时间，故随倾角的增大，小球下落的总时间减少。

图7 小球下落示意图

在高浓度实验中，可以看到，无论试管是倾斜放置还是竖直放置都可观察到沉降的过程中大量沙粒做上下翻滚运动，且当倾角小于90°时，沉降在短时间内就可完成。并且在其他条件不变的前提下，沉降时间随倾角的增大而增大，这与低浓度时的情况截然相反。究其原因，当大量的颗粒同时向下运动时，本来处于试管底部的流体收到挤压而迅速沿颗粒间的空隙相上运动。由于颗粒浓度较大，空隙较小，这股流体会不断与颗粒碰撞，宏观上看，就像颗粒整体受到了流体的“阻滞”，其整体沉降的速度自然会减慢。而试管倾角越小，颗粒越容易在重力的作用下相互靠拢，从而减小了颗粒间的空隙。空隙的减小使得流体难以从中通过，从而减弱了流体的阻滞效应，所以沉降时间会缩短。

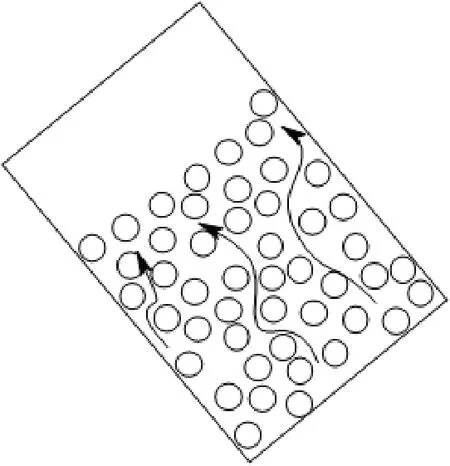
图8 流体运动示意图

5 结论

本文建立了低浓度颗粒沉降与高浓度颗粒沉降有关沉降时间的计算模型，并通过实验进行验证，修正后的模型与实验结果有较好的一致性，可用于分析颗粒沉降过程。在本文的实验条件下且其他条件不变时，单个颗粒沉降的时间随倾角的增大而减小；而高浓度颗粒的沉降时间随倾角的增大而增大。这种现象可以在工业上对沉淀物的分离起指导作用[5]。国外已有报导自来水厂的澄清池中插入斜板以增强悬浮固体的沉降，也有报导将其用于化工领域的例子[6]，相关应用有待进一步的开发和研究。