牵引齿轮传动比对电机轴承温升和换热的影响

刘军强

（中国铁路呼和浩特局集团有限公司大板机务段，内蒙古赤峰 025150）

机车牵引电机轴承是走行部的关键部件。其故障严重时，会导致牵引电机转子轴固死，危及行车安全。机车走行部车载监测装置用于监测轴承冲击和温度信息。监测轴承的温度与冷却空气的温差称为温升，是评定轴承状态的重要指标。温升超过55℃时输出温度报警，影响机车正常运行。机车运行速度相同时，走行部齿轮传动比变大，牵引电机轴承转速的明显提高，导致轴承黏性耗散热量增多，直接影响轴承温升变化。轴承温升受轴承热源及外部换热2方面因素影响。

近年来，杨咸启、宁练等人分别基于数值计算和FLUENT软件模拟对通用滚动轴承和风力机滚动轴承温度场进行了研究［1-2］，然而上述研究中对轴承散热方面的对流换热系数值未明确说明，直接影响其研究结果的可靠性。徐建宁等基于ANSYS软件对油井采油设备齿轮箱轴承温度场进行了模拟分析［3］，然而齿轮摩擦生热引发的轴向导热和润滑油的换热，致使轴承温度场边界复杂化，影响其研究结果。部分研究者对动车组及机车牵引电机轴温开展了现场试验的定性及定量研究［4-6］，未能建立具体的温升模型，同时没有深入研究通风系统对牵引电机轴温的影响。内燃机车牵引电机轴承主要由通风机强制通风及电机转子转动时的空气进行冷却，导致其空气速度场极为复杂，致使软件模拟及在相似原则指导下的试验研究均较为困难。

目前，文献［7］从热平衡角度出发，应用集中参数法构建了牵引电机输出端轴承（以下简称轴承）温升模型。该模型参数表明，轴承温升与走行部齿轮传动比的平方呈正关联，然而该文献仅讨论走行部齿轮传动比为4.5对DF4D型货运机车轴温的影响程度。本研究选取齿轮传动比分别为2.6、3.0、4.5的3类客运机车，结合在同一区段、同一客运车次的轴温数据进行分析。为了降低机车速度不断变化引发的热惯性对瞬态采集数据处理时的影响，保证数据处理结果的准确性，分别对牵引电机功率耗散温升、轴承油脂黏性耗散温升采用时均值的数据处理方法进行对比分析，其分析结果为进一步深入研究牵引电机轴承换热特性及现场轴温数据分析提供参考。

1 温升模型及实测数据处理方法

文献［7］中忽略牵引电机转子轴导热、齿轮摩擦生热、电机体内壁面的辐射换热，从牵引电机进出口温差及轴承油脂黏性耗散研究，根据牵引电机输入功率、输出效率、冷却空气通风量、冷却空气物性参数、机车速度、轮径、传动比、轴承结构尺寸、轴承油脂等参数见表1，构建了轴承温升模型，其公式为式（1）、式（2）：

表1 牵引电机输出轴承温升模型参数

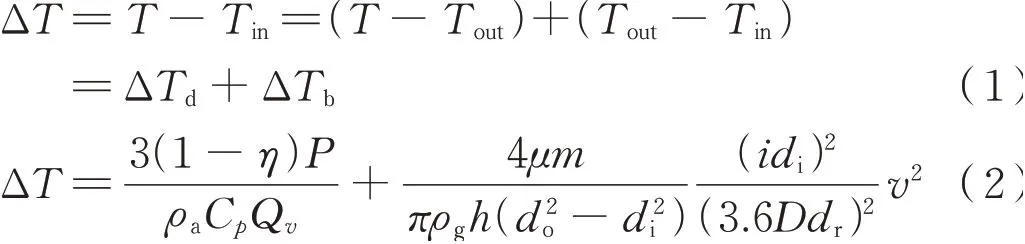
式（1）中：ΔT为牵引电机输出端轴承温升，即轴承测点温度与通风机入口空气温度差值；T为轴承测点温度；Tin为牵引电机通风机入口空气温度；Tout为牵引电机出口空气温度；ΔTd为牵引电机进出口空气温度差值；ΔTb为轴承测点温度与牵引电机出口空气温度差值。

1.1 轴承温升模型修正

式（2）中，对流换热面积为轴承环面为式（3）：

因轴承转动时，内圈运动，外圈静止。沿着轴承旋转中心径向速度变化，轴承座及端盖内空气较多，热阻变大，散热削弱明显。因此，轴承散热以径向为主，其对流换热面积视为外圈滚道的包络区域，为式（4）：

结 合 式（3）、式（4），修 正 后 的 温 升 模 型为式（5）：

式中：等式右边第一项简称为功率耗散项温升ΔTd，第二项简称为油脂耗散项温升ΔTb。由于轴承油脂参数、轴承结构尺寸为常量，在轴承状态及油脂状态良好情况下，机车运行速度一定时，其中油脂耗散项正比于走行部齿轮传动比i平方。为了定量研究走行部齿轮传动比对牵引电机轴承温升的影响，应对电机体进出口温差及油脂黏性耗散引发的温升分别根据机车实测数据的时均值进行计算处理。

1.2 区段ΔTd时均值的数据处理方法

牵引电机进出口温差ΔTd直接与电机功率相关。机车在区间运行时，由于线路坡度变化，不断调整。在一定区段内需加载或减载，柴油机转速也随之改变。该调整过程牵引电机功率损耗量随着牵引电机输入功率而改变，导致热惯性现象更为显著，因此某时刻牵引电机轴温为非稳态的测量值。为了降低热惯性对测量值的瞬态影响，选取该区段内的柴油机转速的时均值所对应的牵引电机输入功率，进一步计算牵引电机功损项产生的进出口温差ΔTd。固定区段内柴油机转速时均值为式（6）：

根据机车柴油机转速时均值，可依据柴油机转速与功率曲线图核算出输出功率，对应牵引电机输入功率。对DF4D型内燃机车柴油机转速nmax标定为1 000 r/min时，柴油机输出功率Pc（nmax）为2 200 kW；机车运行时柴油机满载最高转数时的进出口温差计算为式（7）：

通风机通风量与柴油机转速正比关系，可得柴油机转速为n（单位：r/min）时的通风机通风量为式（8）：

式（8）中柴油机转速为n（单位：r/min）对应的柴油机输出功Pc（n）时，单个牵引电机进出口温差ΔTd和时均值可表示为式（9）：

式（9）忽略空气密度影响，即ρa，max/ρa=1，ΔTd时均值表示为式（10）：

1.3 区段ΔTb时均值的数据处理方法

DF4D型内燃机车共用6台牵引电机驱动，如图1所示。

图1 DF4D型内燃机车牵引电机测点编号分布图

从Ⅰ端至Ⅱ端，牵引电机输出端测点温度依次为T1～T6。该研究遵循上述规定，对t时刻第i台牵引电机轴承温度及温升依次标定为Ti（t）及ΔTi（t）。所以，t时刻全车6台牵引电机温升的均值计算为式（11）：

在给定区段内，牵引电机体内冷却空气视为不可压缩流体，机车持续运行tN时间段时的温升时均值用积分均值方法计算为式（12）：

根据式（1），轴承油脂黏性耗散温升时均值可表示为式（13）：

结合式（6）～式（13），可计算出区段ΔTb时均值，该值用于讨论牵引传动比对轴承换热的影响。

2 结果及讨论

应用机车走行部车载监测装置的实测数据，对同一区段、同一车次选取了3类不同传动比的客运机车。某区段线路长度L为100.3 km，其客运（货转客）机车牵引运行时间t为74 min，该区段内机车速度v均值是81.5 km/h。

选取3类DF4D型内燃机车，其对应走行部齿轮传动比依次为2.6、3.0、4.5，构造速度为170、150、100 km/h，见表2。

表2 不同构造速度车型对应的牵引齿轮传动比

所选DF4D型内燃机车牵引电机输出端均安装E32330EQTU型滚柱轴承，轴承尺寸相同、油脂质量相同，忽略轮径不同引发的温升变化，机车在该区段的速度时均值v一样。式（5）中ΔTb时均值可简化为式（14）：

式（14）表明，轴承油脂黏性耗散引发的温升均值正比于传动比i的平方，反比于对流换热系数h。对流换热系数与牵引电机体内空气流速密切相关，当传动比变大时，经由牵引电机体内的冷却空气对轴承的对流换热效果增强。本研究根据机车运行实测数据的时均值，分别从电机进出口温差、传动比对轴承与冷却空气间的对流换热强度、传动比对轴承油脂黏性耗散温升等3方面分析讨论。

2.1 进出口温差ΔTd时均值的结果及分析

3类机车在该区段内柴油机转速随时间的变化曲线如图2所示。

图2 3类机车柴油机转速随时间曲线图

应用LKJ数据分析软件，每隔3 min记录相应柴油机转速。因该区段多处线路为V型，即机车在加载与减载调整过程，坡顶减载，接近坡底从最低转速加载。从图2可知，3类机车柴油机转速均出现最低转速加载现象。根据式（6）计算，传动比从小到大柴油机转速在该区段内的时均值依次为790、797、805 r/min。该3条时均值数据基本一样，可视为柴油机输出的功率均值一致，即转速n的时均值为800 r/min时，对应柴油机输出功率时均值为1 000 kW。忽略主发输出效率影响，当柴油机最高转速nmax为1 000 r/min时，对应输出功率Pc（nmax）为2 200 kW。单台通风机最大通风量Qv，max为5.5 m3/s；冷气空气密度ρa取10℃标准大气压下干空气密度值，1.25 kg/m3。因牵引电机进出口压差约4 kPa，空气定压比热容Cp取1.005 kJ/（kg·K）。牵引电机输出效率η取0.93。将以上参数代入式（7），可计算出柴油机最大输出功率下对应的牵引电机进出口温差ΔTd，max为式（15）：

式（15）结果表明，在特定参数下，柴油机最大输出功率下牵引电机进出口温差为13℃。

因此，在柴油机转速时均值为800 r/min，输出功率1 000 kW时，将上述值代入式（8）、式（10），可得单台通风机通风量和进出口温差ΔTd时均值分别是为式（16）、式（17）：

式（16）、式（17）结果表明，在整个区段内牵引电机通风机通风量均值为4.5 m3/s，牵引电机进出口温差均值为6℃，进出口温差均值对不同传动比的电机温升均值影响结果相同。

曲线为3类机车在该区段运行时不同时刻对应的全车牵引电机轴承温升均值如图3所示。该曲线表明，机车传动比越大，同一时刻对应的温升值随之增大。在初始阶段的前10 min内，由于热惯性导致异常。初始阶段，机车速度增大时，温升反而降低。形成该现象的原因是，机车站停后，柴油机在最低转速下通风机通风持续冷却牵引电机体，其内积聚的热量短时间及时散失，待机车加载加速运行时，电机体内铜损、铁损等原因，导致电机体缓慢变热。然而电机体加热的速度小于冷却空气散热速度，致使牵引电机进出温差持续变小，导致温升变小。结束阶段的异常现象反之。根据图3数据，联立式（12）、式（13），可得该区段及时间段内传动比2.6、3.0、4.5对应的黏性耗散温升ΔTb时均值是分别是12、13、16.8℃。

图3 机车速度v、温升ΔTb随时间曲线图

2.2 传动比对轴承换热的影响分析

机车以恒定速度v运行时，根据式（5），牵引电机轴承油脂黏性耗散引发的温升为式（18）：

式中：K为常数。

根据文献［8］中的牛顿冷却公式可知，轴承油脂耗散热量的热流密度及对流换热系数为式（19）：

式（19）表明，轴承对流换热的热流密度存在正比对应关系。

i2随ΔTb时均值变化的曲线如图4所示，其中i2间接反映了黏性热源产生热量的多少。从图中可知，传动比2.6、3.0、4.5对应的黏性耗散温升ΔTb的时均值分别是12、13、16.8℃，则传动比平方i2与对应黏性耗散温升时均值的比值分别是：0.56、0.70、1.56，其中该项比值从0.56变为1.56时提高值为（1.56-0.56）/0.56，结果为1.78倍。

图4 i2随ΔTb时均值变化曲线图（i为传动比）

上述3个比值数据间接表明，在机车速度及通风机通风量一定（柴油机转速相同）的情况下，随着传动比的增大，通风系统对轴承的对流换热系数h增大，对流换热强度提高1.78倍，轴承冷却效果增强显著。形成该现象的主要原因是，虽然齿轮传动比增大，导致电机转速升高，油脂黏性耗散热量增加值为（4.52-2.62）/2.62，结果为2倍。然而电机转子转速升高的同时，加速了体内空气的扰流效应，提高了对流换热强度，强化了对轴承的换热，致使轴承冷却效果更为显著。因此，传动比从2.6变为4.5时，其黏性耗散热量增加了2倍，因转子转动扰流效应增强，强化了轴承换热，对流换热强度提高了1.78倍。

2.3 传动比与ΔTb时均值的关联式及分析

ΔTb均值随传动比i的变化曲线如图5所示。该曲线共3对数值，拟合后的关联式为式（20）：

图5 ΔTb时均值随i变化曲线图（i为传动比）

式（20）表明，温升时均值正等于传动比。定义φ=ΔTb代入式（18），则为式（21）：

式（21）中，φ对i、h全微分，可得式（22）：

式（22）中，空气对流换热h的数值在10～100之间，i2/h2为小量，忽略该小项，则式（22）可简化为式（23）：

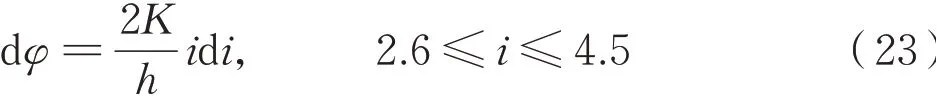
式（23）表明，虽然ΔTb变化量与传动比i呈正关联，然而机车运行时，随着i的增大，对流换热系数h随之增大，导致其变量2Ki/h的值变化非常小，趋近于常数2.5。

3 结论

机车以一定速度运行时，走行部齿轮传动比不同导致牵引电机输出端轴承转速发生变化，直接引发轴承油脂黏性耗散热量的增多，轴承温升随之变化。通过在同一区段，同一客运车次，3类不同传动比的客运机车的实测数据对比分析。机车速度的时均值为81.5 km/h，柴油机运行转数时均值为800 r/min，通风机通风量4.5 m3/s时，结论如下：

（1）模型中轴承油脂黏性耗散引发的温升与传动比平方呈正关联。然而，随着传动比的增大，由于对流换热强度的增强，实测数据显示为线性关系，其斜率为2.5。传动比从2.6变化为4.5时，轴承黏性耗散引发的温升增加4.8℃。

（2）机车速度和电机通风系统主流速度相同时（通风机通风量相同），牵引电机转子转动强化了轴承油换热。齿轮传动比从2.6变为4.5时，黏性耗散热量增加了2倍，转子转速提高致使扰流效应增强，对流换热系数h变大，对流换热强度提高1.78倍。