基于响应面模型的锚支护机组立柱多参数优化
徐诗虎,邓海顺 ,苏国用 ,王文善
(1. 安徽理工大学 机械工程学院,安徽 淮南,232001;2. 安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南,232001)
随着煤矿智能化目标的提出,学者们在掘锚支一体化系统理论方面开展了大量研究,并研制了多款国产掘锚联合机组[1-2],但受制于掘进工作面空间狭小、巷道底板潮湿易下陷等问题,迈步式锚支护机组的普及具有局限性,而立柱作为核心部件,其动态性能直接决定了整机的工作稳定性[3]。若立柱采用较轻质量,在移动过程中能够减少运动惯性和变形,有效降低井下作业的危险性,因此,在投入生产前优化结构尺寸,对于设备的运行性能极为重要。
对于立柱的优化设计,王雷等[4]采用响应面与遗传算法相结合的优化设计方法,得到了Pareto最优解集;蒲凡等[5]建立了立柱动静态特性的联合拓扑优化数学模型,利用 ANSYS 软件对其结构进行多目标拓扑优化设计;童水光等[6]利用起重机刚性支腿的参数化有限元模型和BP神经网络,采用混合遗传算法引导遗传算法的搜索方向;孙晓俊等[7]对立柱进行模态分析,通过灵敏度分析得到关键尺寸参数;陈静等[8]对立柱进行拓扑优化分析,依据分析得到的最佳分布和立柱设计经验改进原立柱结构;方阳等[9]利用Python语言编写计算程序,采用多岛遗传算法进行优化,建立一套迭代优化立柱结构的分析流程。
由于大多方法使用的数值模拟复杂且耗时,给优化过程带来过多工作量,基于此,本文对迈步式锚支护机组立柱的结构尺寸参数进行多目标优化,通过灵敏度分析筛选出对体积、最大总位移和一阶模态频率影响最大的4个待优化参数,通过最优空间填充设计法建立响应面模型,利用遗传算法进行循环迭代优化,最后,将优化后的模型进行对比验证。
1 基于响应面模型的参数确定
1.1 立柱的模态分析
某迈步式锚支护机组立柱为套筒式结构,上顶端与机身进行铰支连接,另一端与地面接触。立柱采用304不锈钢材质,密度ρ为7 930 kg/m3,泊松比μ为0.29,弹性模量E为1.99×1011Pa,许用应力[σ]为137 MPa,采用SolidWorks进行三维建模,在建模时,圆角、倒角、小直径孔等特征会增加后续仿真计算量,因此,需要对整体结构进行简化,通过设置参数调试网格,网格尺寸设置为5 mm;对顶板、侧壁开孔处、底板和筋板等应力集中处进行细分网格,设置尺寸为4 mm的面网格,最后生成234 326个节点和125 666个单元,立柱实物图和生成的有限元网格模型见图1。
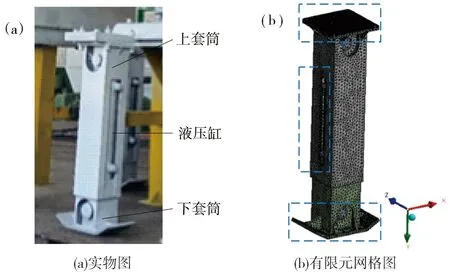
图1 迈步式锚支护机组立柱
立柱通过螺栓孔与机身相连,因此,对上套筒顶板的螺栓孔添加固定约束来模拟边界条件进行模态分析,得到立柱前四阶固有频率和振型,见图2。整机是个具有多自由度的振动系统,其运动都可以由各低阶固有振型的线性组合来表达,高阶振型阻尼较高,则其动态特性的影响明显低于低阶振型,因此,模态分析集中在对结构影响较大的低阶模态上[10]。
1.2 立柱参数的灵敏度分析
在对结构尺寸进行优化设计时,设计变量的灵敏度可反映其与目标函数的关联,对于优化过程的求解效率、可行性设计都有影响[10]。该立柱尺寸参数较多,为了减少优化时的计算量,需要在ANSYS的参数相关性模块(parameters correlation)进行一次灵敏度筛选[11],找出对立柱性能影响大的关键尺寸。本次优化只考虑约束函数对目标函数的影响,采用K-T条件进行计算,即:
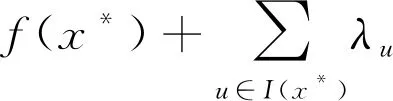
(1)
式中:x*为约束最优点;gu(x*)为不等式约束;hv(x*)为等式约束。其中不等式约束和等式约束可写成:
(2)
式中:φv(x*)和φu(x*)为常数;bv和du是约束条件中发生变差的参数,则约束条件对目标函数的灵敏度可写成:
(3)
采用spearman法对12个输入变量各生成200个样本点,输出参数选择体积、最大总位移和一阶模态频率,设置好后计算样本点参数,运行程序后得到的敏感度分析结果见图3。
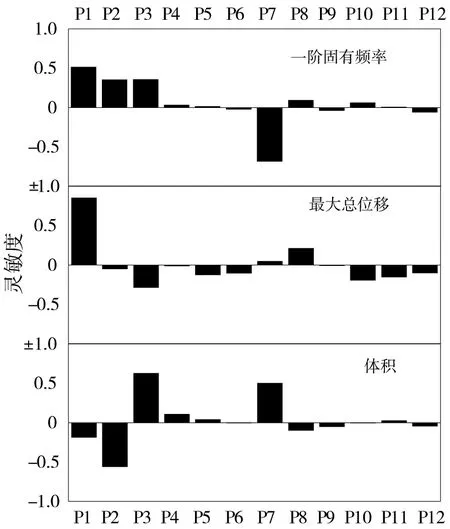
图3 设计变量灵敏度分析结果
对立柱体积影响最大的是P2上套筒开口长度、P3上套筒开口宽度和P7套筒厚度;对立柱最大总位移影响最大的是P1顶板厚度和P7套筒厚度;对立柱一阶模态频率影响最大的是P1顶板厚度。灵敏度分析结果为正表示设计参考点处梯度为正,输入变量与输出变量呈正相关关系,灵敏度为负则相反。根据灵敏度分析结果选择4个待优化设计点参数P1(x1)、P2(x2)、P3(x3)和P7(x4),结构尺寸参数见图4。
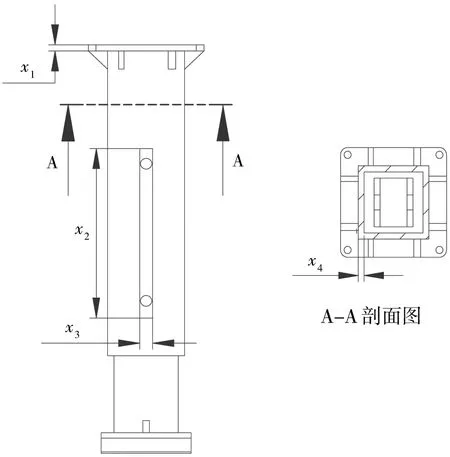
图4 立柱待优化参数示意图
1.3 立柱响应面模型的拟合
响应面模型分析法的核心就是用特定试验设计方法,得到目标函数和约束函数的响应面模型,并预测非试验点的响应值[12-13],可采用不同阶次多项式表达目标与设计参数之间的关系,其近似模型为
(4)
式中:y为输出变量;a为多项式系数;xi为设计变量;n为设计变量个数;待定次数a0、ai、aii、aij个数为(n+1)(n+2)/2。
检验响应面模型拟合精度的常用准则是相对均方根误差(root mean squared error, RMSE),其可表示响应面模型得出的仿真值与实际值之间的差异程度,差值越小则拟合精度越高[14],其定义如下:
(5)
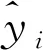
为得到准确合理的试验点,采用响应面最优空间填充设计(optimal space-filling design)在整个设计空间均匀抽取分布点,每个参数生成40个样本进行计算,以立柱体积、最大总位移和一阶固有频率为输出目标函数,得到对应的输入变量约束条件,计算后采用无交叉项的标准二阶响应面评估样本点拟合情况,由图5可知,各设计点生成的响应面与试验设计的样本点之间拟合精度较好,基本都分布在对角线附近,可以进行下一步优化。
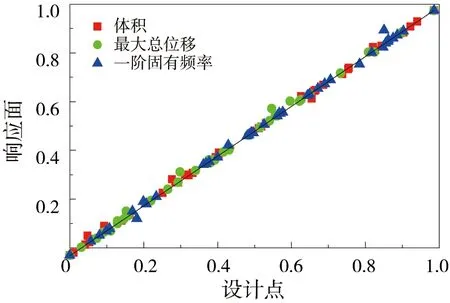
图5 响应面拟合优度曲线
2 基于遗传算法的参数优化
2.1 建立立柱数学模型
本次优化的首要目标是立柱轻量化,首先,将多目标函数转化为单目标函数,进行归一化处理,建立权衡函数[15]为
(6)
式中:ti表示
(7)
式中:n为设计变量个数;f*和f(x)分别代表第i个目标函数的理想可行解和实际值;fmax和fmin分别代表目标函数最大值和最小值。
对立柱的优化目标是在满足性能要求的前提下,实现轻量化设计,以此构建目标函数和特征参数约束(筋板等非影响因素不考虑):
minV(x)=V上+V下=Sx1-x2x3+H1[L2-(L-2x4)2]+H2[(L-2x4)2-(L-4x4)2]=3.2x1-x2x3+45.6x4-74x42
(8)
式中:V上和V下分别为上套筒和下套筒的体积;S为顶板截面积;H1和H2分别为上套筒和下套筒的长度;L为套筒外侧壁宽度。设置好后,进行各参数的优化。
2.2 立柱优化过程及结果
使用MATLAB工具箱的遗传算法(genetic algorithm,GA)对以上优化方案进行求解,能够对多变量优化问题进行全局寻优。设置种群规模为60个,交叉概率为0.7,变异概率为0.01,最大进化代数为60代,设置完毕后进行迭代得到Pareto最优解,各代最佳适应值和平均适应值变化曲线见图6。

图6 目标函数与遗传代数的关系
目标函数在第39代时最佳适应值曲线和平均适应值曲线都收敛,达到最优方案,设计变量优化值取整后见表1,优化后的立柱顶板与套筒厚度有所减少,侧壁开口增大,总体质量减小22.45%,因此,对立柱的优化达到了轻量化的目标。

表1 优化变量对比
3 立柱动态特性对比分析
通过ANSYS Workbench对优化后的立柱添加相同的边界条件进行模态分析,并与优化前立柱模态分析结果进行对比,见表2,由表2可知,优化后的立柱各阶振型形式相同,前三阶固有频率都有较大提升,分别提高了48.97%、52.17%和66.76%,大于立柱发生最大振幅时的激励频率,表明立柱结构更加稳定,因此,对立柱的优化达到了增加低阶固有频率的目标。
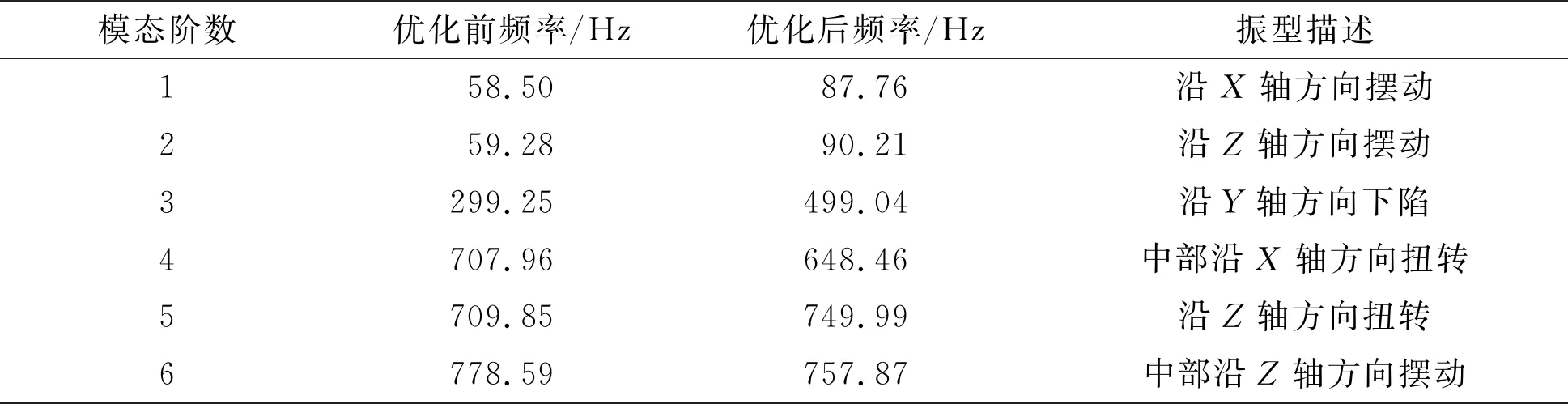
表2 固有频率对比与振型描述
接下来探测立柱在收到周期性载荷时的振动特性,在ANSYS中打开谐响应模块对优化前后的立柱施加相同简谐激振力,得到受迫振动下立柱的三向位移-频响曲线[16]。由图7可知,优化后的立柱在X向、Y向的位移峰值下降明显,Z向由于侧壁开口增大,其位移增加不可避免,但是增量较小。工作时应尽量避免50~70、490~510和740~760 Hz的3个位移响应比较大的频率区间,总体来看,改进后的立柱动态性能较好,因此,对立柱的优化达到了改善动态性能的目标。
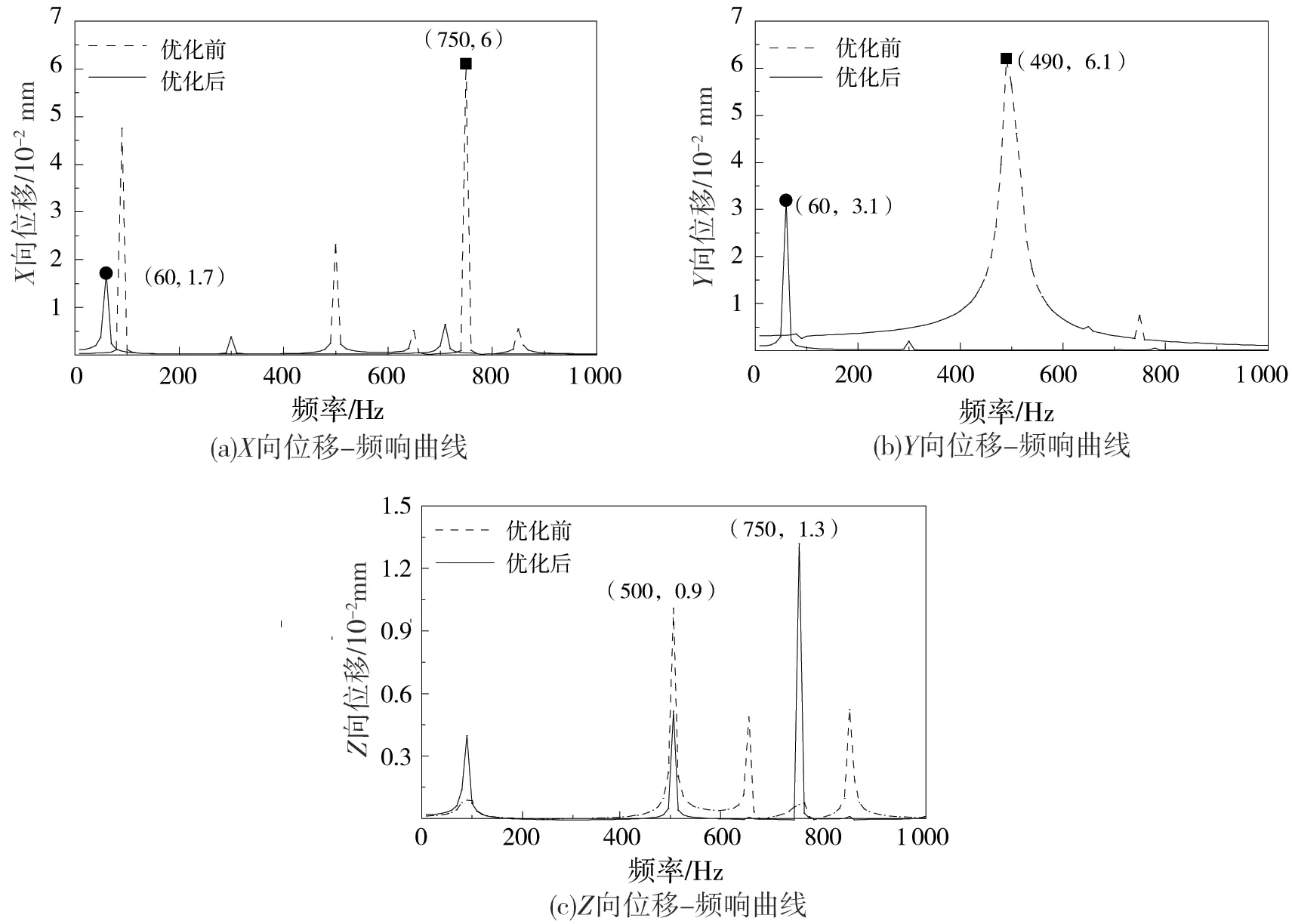
图7 三向位移-频响曲线
4 结语
1)根据模态仿真分析和灵敏度筛选结果进行立柱响应面的拟合,通过RMSE准则验证拟合精度;采用最优空间填充设计在设计空间内抽取样本点,结果表明:各设计点生成的响应面与试验设计的样本点之间拟合精度较好,可以进行下一步优化。
2)建立立柱优化数学模型,使用MATLAB工具箱的遗传算法对其进行迭代求解,在第39代时得到最优方案,此时总体质量减小22.45%,因此,对立柱的优化达到了轻量化的目标。
3)对优化前后的立柱进行动态特性仿真,优化后的立柱各阶振型形式与优化前相同,前三阶固有频率分别提高了48.97%,52.17%和66.76%,大于立柱发生最大振幅时的激励频率,表明立柱结构更加稳定,因此,对立柱的优化达到了增加低阶固有频率的目标;优化后的立柱在X向、Y向的位移峰值下降明显,且预测到工作时应尽量避免50~70、490~510和740~760 Hz的3个位移响应比较大的频率区间,因此,对立柱的优化达到了改善动态性能的目标。

