基于优化的VMD-CNN-LSTM模型的光伏功率预测

吴勇，高昕，郭灏阳，刁海岸，刘庆丰，杨强强

(安徽理工大学 电气与信息工程学院，安徽 淮南，232001)

光伏发电受各气象因素影响，输出功率曲线具非线性和非平稳性，其并网不仅影响了电网的电能质量，还会给负荷经济调度带来困难,因此提升光伏功率预测精度的模型已成为解决光伏发电规划问题的重要工具[1-2]。传统的功率预测模型在处理复杂数据和结果精度等方面占优，但针对存在波动性和时序性特点的光伏功率数据处理方面仍有不足之处。

赵建利等[3]结合卷积神经网络(convolutional neural network,CNN)和长短期记忆(long short-term memory,LSTM)网络构建了风电功率预测模型，通过CNN结构的堆叠作用，抽取出历史数据中的特征量，并降低冗余数据量输入到神经网络。包苑村等[4]在赵建利等[3]的基础上加入了变分模态分解(variational mode decompositon,VMD)针对非线性的月径流时序进行组合预测，较经验模态分解(empirical mode decomposition,EMD)法可以主观防止出现中心频率混叠的问题，且预测结果的峰谷值的拟合优度较高。朱宗玖等[5]将CNN与门控递归单元( gated recursive unit，GRU)模型相结合，可以有效判断功率曲线的变化规律，精准分析在峰值阶段，输入数据特性对预测功率带来的影响。胡威等[6]引进麻雀搜索算法(sparrow search algorithm,SSA)优化VMD的关键参量，采用LSTM神经网络搭建组合预测模型，不仅考虑了动态电价和湿度等多类环境变量，还利用最大相关最小冗余算法剖析了分解量和负荷间的关联性，得到所需模型的最佳输入样本。

为进一步提高光伏功率的预测精度, 针对VMD用经验知识定义模态数和传统功率预测方法缺少对时序数据考虑等问题，本文设计了一种新型深度融合网络组合模型(CS-VMD-CNN-LSTM),引进布谷鸟搜索(cukoo search,CS)算法优化VMD参数，用CNN提取模态分量的时域特征,再通过LSTM叠加预测结果,实验证明了本文方法的有效性。

1 方法与理论

1.1 变分模态分解

VMD是一种自适应、完全非递归的信号分解处理方法，主要探究变分问题的构造和求解[7]，适用于分解非线性信号，得到多个不同递减频率且相对平稳的模态函数。VMD算法重新定义了约束条件更为严格的有限带宽本证模态函数，表达式为

Uk(t) =Ak(t)cos[φk(t)]

(1)

式中：k为模态数；Ak(t)为信号Uk(t)的非负包络幅值；φk(t)为瞬时相位函数。

VMD将信号分量均当作聚积在自中心带宽周围的窄带信号，并依据本证模态函数条件设置约束优化问题的模型，进而确定各模态分量的中心频率乃至重组后的对应分量。VMD约束变分模型如下：

(2)

式中：wk为各模态的中心频率；δ(t)为狄拉克函数；*为卷积运算符；f为原始信号。

为消除上述式中的约束优化问题，可通过增广拉格朗函数将上述等式等效为一个无约束优化问题，通过交替方向乘子法来求解,得到当前模态分量uk和中心频率wk表达式：

(3)

(4)

式中：n为迭代次数；w为频域符号标志；α为惩罚因子；λ为拉格朗日乘子。

1.2 CS算法

CS算法是一种新兴的基于自然元启发式的最小值寻优算法[8-9]，通过初始化鸟窝适应度值，不断迭代，更新出最优鸟窝方位(xbest)和最优解(fmin)。CS优化算法寻求最佳鸟窝的方位和最优路径的表达式如下：

(5)

式中：m为迭代步数；n为鸟窝数；β为步长控制量；L为莱维随机行走搜索路径；s为随机步长，其步长稳定符合一个重尾的概率分布。

1.3 CS优化VMD

VMD相较于EMD分解法可以防止出现两端发散和模态混叠的局面，其分解准确性与模态分解数(K)、惩罚因子值(alpha)息息相关，alpha影响到模态分量的中心频率，K和频率范围影响了时序的选取结果。但选取VMD对时序数据分解时，需依据先验知识设定K、alpha及收敛条件等其他主要参数值。现实需分解时序具有噪音和复杂性，先验设置模态数和惩罚系数相对不易，因此，本文采用CS算法优化VMD的K和alpha。

利用CS自适应优化VMD的重要参数并建立模型时，重要的是以局部包络熵的极小值构建适应度函数，包络熵能够反应原始功率输出序列的稀疏特性[10]。原序列经过希尔伯特变换后得到解析序列，取绝对值构造的包络信号的包络熵Ep函数式如下:

(6)

式中：N为原序列的元素总数；aj为包络信号。

1.4 CNN-LSTM 深度神经网络

CNN包含卷积计算且具有深度结构，区别于其他神经网络，CNN还额外拥有卷积层和池化层结构。卷积层承担提取数据的局部特征，运行时通过次序依次扫视输入数据的特征值，在卷积核范围内对数据特征值用矩阵相乘求和且累加偏差量b，如下：

(7)

式中：特征图Zm为输入和输出的m层；K为Zm的通道数；f、s0、p分别为对应的卷积核大小、卷积步长和填充层数。

传统的循环神经网络(recurrent neural network,RNN)不易提取较长序列方面数据，易导致梯度不稳定。LSTM在RNN的基础上进行改进，引进了新的内部状态和逻辑门控制机制，前者专门通过线性的循环数据传送，后者用来控制数据传达的路径，可提取较长时序数据的内部分布特征。新的内部状态Ct和隐藏层的外部状态Ht表达式如式(8)所示：

(8)

式中：ft、it和ot依次为遗忘门、输入门和输出门。

其核心思路是用遗忘门和输入门有抉择的保存状态控制单元的状态，见图1。

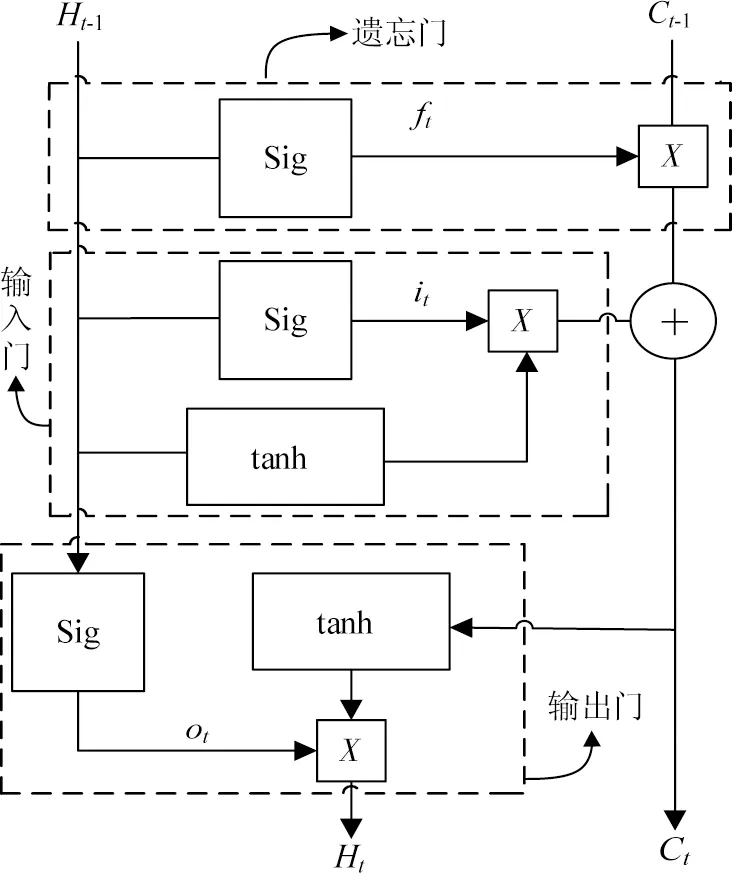
图1 LSTM的基本单元门

结合CNN 和LSTM网络各自的优势，CNN将数个天气特征量组成的多维时序Xt,m和经模态分解后的一条子序列Yt,n作为输入数据。每行t表示具体某一时刻，每列m表示在时间步长t内的具体某一天气特征值，每列n表示模态分解序列号。然后经过卷积和池化操作，得到空间特征，并输出为一维序列。LSTM将获得的一维序列作为输入，从而与全连接层相连接，最终联合空间特征预测值，对实际功率数据进行回归预测。CNN与LSTM结合的 CNN-LSTM 深度网络结构见图2。

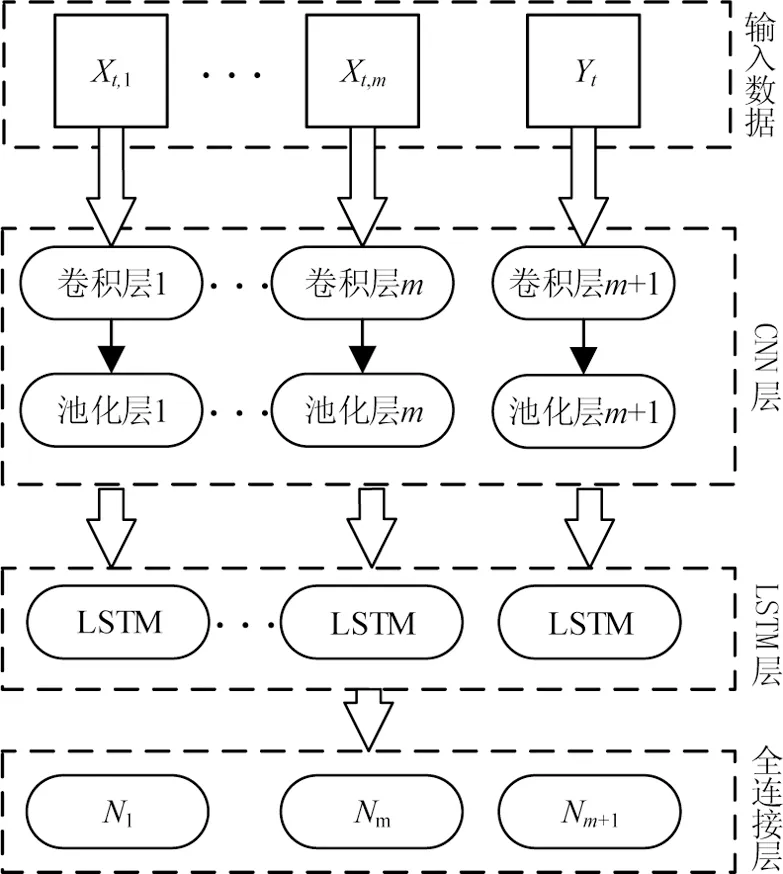
图2 CNN-LSTM组合模型框图

2 CS-VMD-CNN-LSTM组合预测模型

2.1 预测步骤

光伏输出功率容易受到诸如光照辐射、温度、湿度、气压和风速等相关因素的干扰，但原始测试数据维数较多且冗余。灰色关联度分析是一种依据各因素之间发展趋势的相似程度来确定因素之间的关联程度的方法。通过灰色关联度分析法，根据天气特征类型对历史数据进行聚类，来衡量气象因素与光伏发电功率的关联度，见表1。

表1 天气特征向量与输出功率的关联度

由表1可知，总辐射、温度和湿度值与光伏功率数据的关联度最高，因此，舍弃关联度不高的其余天气因素。

首先，通过CS优化后的VMD进行模态分解，来降低光伏功率序列具有的不平稳性；其次，逐一送入具有二维卷积核的CNN神经网络进行特征提取；最后，通过LSTM网络连接全连接层，叠加预测结果。其预测流程见图3。

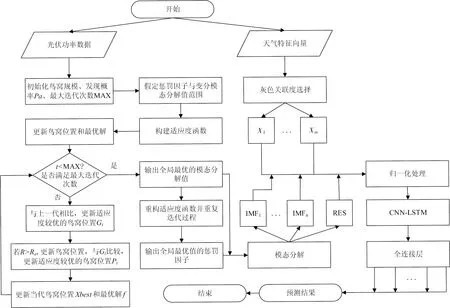
图3 组合预测模型流程图

具体操作步骤如下：1)收集光伏历史功率数据集，包括光伏发电过程中不同时间段的功率数据，并涉及光伏发电时期具多尺度的天气特征数据。2)使用灰色关联度分析将天气特征数据进行聚类，并筛选出与光伏功率值关联度较高的特征向量。3)初始化CS算法的种群大小、迭代次数和鸟窝适应度值等，进行编码。用CS优化算法优化VMD的K和alpha参数值，先确定VMD的模态数和惩罚因子范围。4)假定alpha值，以局部包络熵极小值构建适应度函数，选取较优的一组鸟窝方位X，满足最大迭代次数时输出给定范围内的最优值K。5)根据得到的最优模态分解值，重复步骤4)，满足最大迭代次数时输出给定范围内的最优值alpha。6)依据最优值，将原始光伏功率数据用CS-VMD进行模态分解，自适应分解为多条经过希尔伯特变换后的解析序列。7)将模态分量和保留的天气特征向量均进行最值标准化处理。8)将处理后的特征向量和每个模态分量逐一送入CNN卷积网络，采用二维的卷积层提取上述组合量的隐含特征，每个组合量对应输出的一维组合序列。9)LSTM将一维组合序列作为输入，对光伏功率进行回归预测。LSTM网络包含多个逻辑门控单元，这些逻辑门控单元的输出都可以与全连接层相连，通过计算全连接层中神经元的平均值，得到光伏功率模态分量的预测结果。10)累加各模态分量的预测值并检验组合预测算例的精度，进行评估。

2.2 预测模型评定

本文在评估不同组合预测算例的准确性标准方面，因预测的光伏数据存在较多零序列，权衡采用平均绝对误差(mean absolute error,MAE)和均方根误差(root mean square error,RMSE)作为评估指标，其表达式如下：

(9)

(10)

式中：Xt和Xp分别为第m个数据点的原本光伏功率值和预测光伏功率值。

3 模型仿真

选取宁夏太阳山光伏电站(12 MW) 2017 年3月初至8月底全天天气的光伏输出功率作为研究的数据集，采样频率为15 min，即每天采样 96个样本点。本文采用该光伏电站前五个月(共计1 468个数据点) 作为训练样本，使用灰色关联度分析法选取与预测时刻关联度较高的太阳辐射、温度和湿度方面的天气特征向量作为模型训练输入，对8月份实际光伏输出功率进行整体预测。

3.1 功率时序分解

对原始光伏功率时序进行分解，采用 CS优化VMD设置参数，其中，CS种群大小P为10，发现外来鸟蛋概率Pa为0.25，假定模态分量k和惩罚参数alpha寻优范围分别为3到10、100到2 000，从而减小模型运行时间。以局部包络熵极小值构建适应度函数，来更新鸟窝方位和最优值，最优值代表了模态数和惩罚因子值。根据最优值，VMD将光伏输出功率数据分解为解析序列IMF1-IMF6和保留的RES分量，分解结果见图4。其中：最优值K和alpha分别为6和163.58；最小的局部包络焗为12.52。图4中7个分量具有周期性，频率依次递增，IMF1在6种分量中占比最大，RES分量代表原始光伏功率时序的趋势变化。

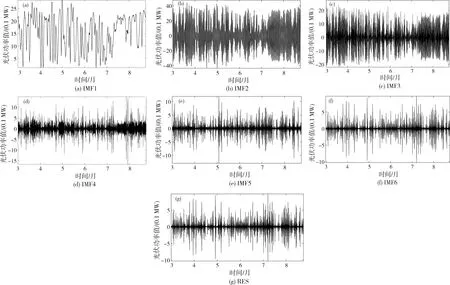
图4 光伏功率的VMD分解结果

3.2 CNN与LSTM参数模型选择

根据历史功率数据的变化规律，将CS-VMD分解的模态数逐一作为CNN-LSTM网络训练集和测试集的输出，通过灰色关联度分析法筛选出天气特征集作为训练集和测试集的输入，用来仿真运行。CNN负责提取原始数据的特征，该模型通过两层卷积核与一层池化层对时序数据提取特征量，采用最大池化方式，后接LSTM层，对时序数据提取内部分布特征，并以全连接层整合输出预测曲线。LSTM层数的确立尤为重要，即隐藏层层数，在测试数据足够多的情况下，增加层数能够增强模型的非线性拟合性能和预测精度，然而也使得模型更为复杂，延长了模型运行时间，甚至引发过拟合问题，因此，本文将隐含层网络结构限制在3层。

3.3 对比实验和算例分析

确立CS-VMD-CNN-LSTM 模型的每个子模块具体参数后，将各模态分量依次送入组合深度神经网络与天气特征值进行训练得出各光伏功率分量预测值，最终累加每一分量模型的输出视为光伏功率的预测值，并与实际功率曲线对比，分析其有效性。并搭建CNN-LSTM，EMD-CNN-LSTM，VMD-CNN-LSTM和GA-VMD-CNN-LSTM等模型与本文提出的CS-VMD-CNN-LSTM模型进行对比实验分析，其中，CNN-LSTM网络以未分解的历史光伏功率值作为模型输入，其余模型预测过程均与本文一致，上述模型的8月份前5天预测结果见图5。

光伏功率曲线具非平稳性且变化范围较广，难以看出上述预测结果的对比精度。从全局角度，图5中各模型的最终预测结果和规律性走势大相庭径，这是因为预测算例均基于深度融合CNN-LSTM神经网络的原因。不同模型在峰值处的功率预测结果更为精准，但在夜间零功率预测方面均存在不足。

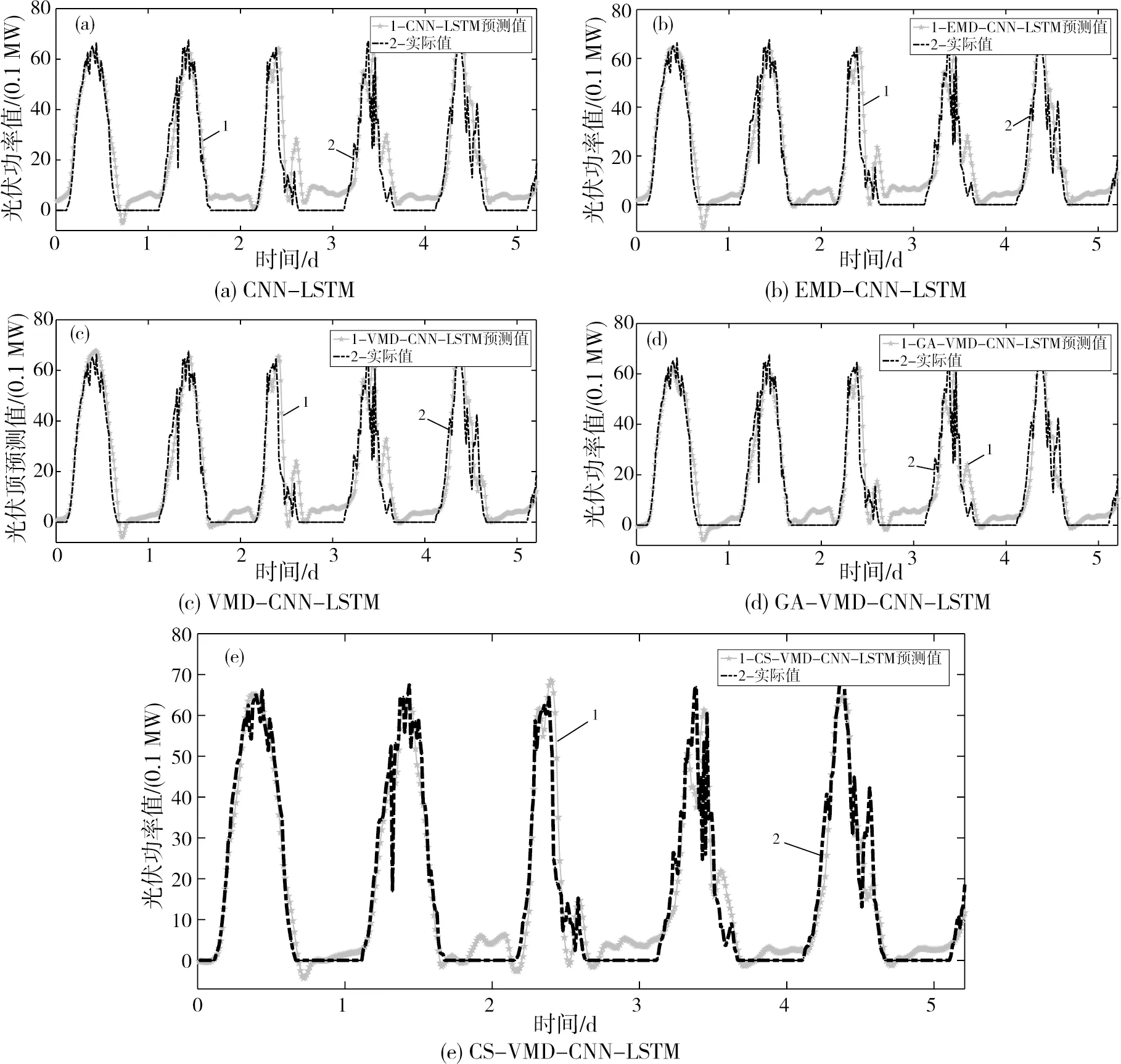
图5 不同模型的预测结果

为进一步探究各模型的预测准确率，具体某一天的日出力预测结果见图6，各预测结果评估指数见表2。在数据处理方面，加入优化后的模态分解组合模型对训练光伏功率数据表现的性能更佳。

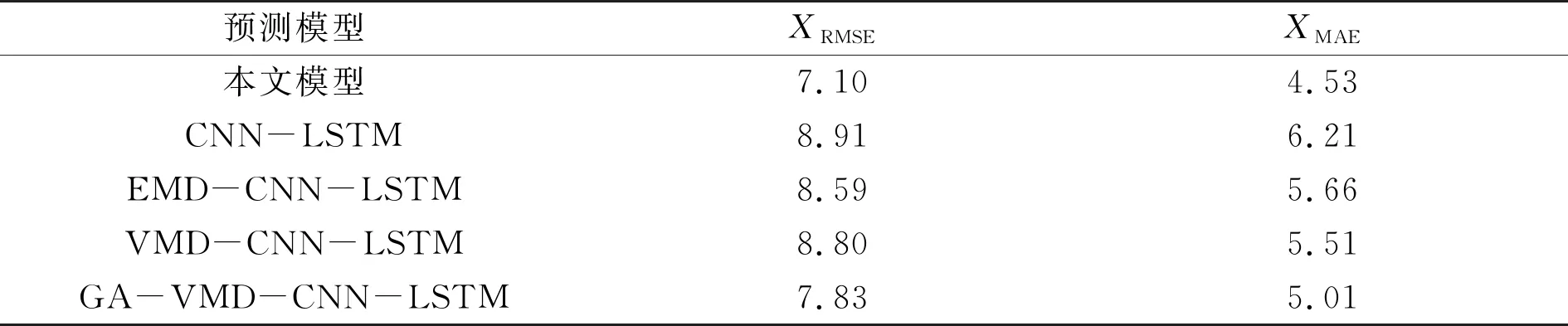
表2 不同预测模型的预测指标

图6中，当处于更为复杂的云层分布环境下，实际光伏功率曲线更具随机性和波动性；5个模型都可以规律性地进行预测，且提出的CS-VMD-CNN-LSTM 组合模型预测结果最贴近实际功率曲线；在预测峰值时，单CNN-LSTM和加入VMD后的CNN-LSTM模型表现均达不到更好效果；相比之下，所提模型较于GA优化的VMD参数，更能提取出数据特征，有效学习光伏功率的变化趋势，保证了预测精度。

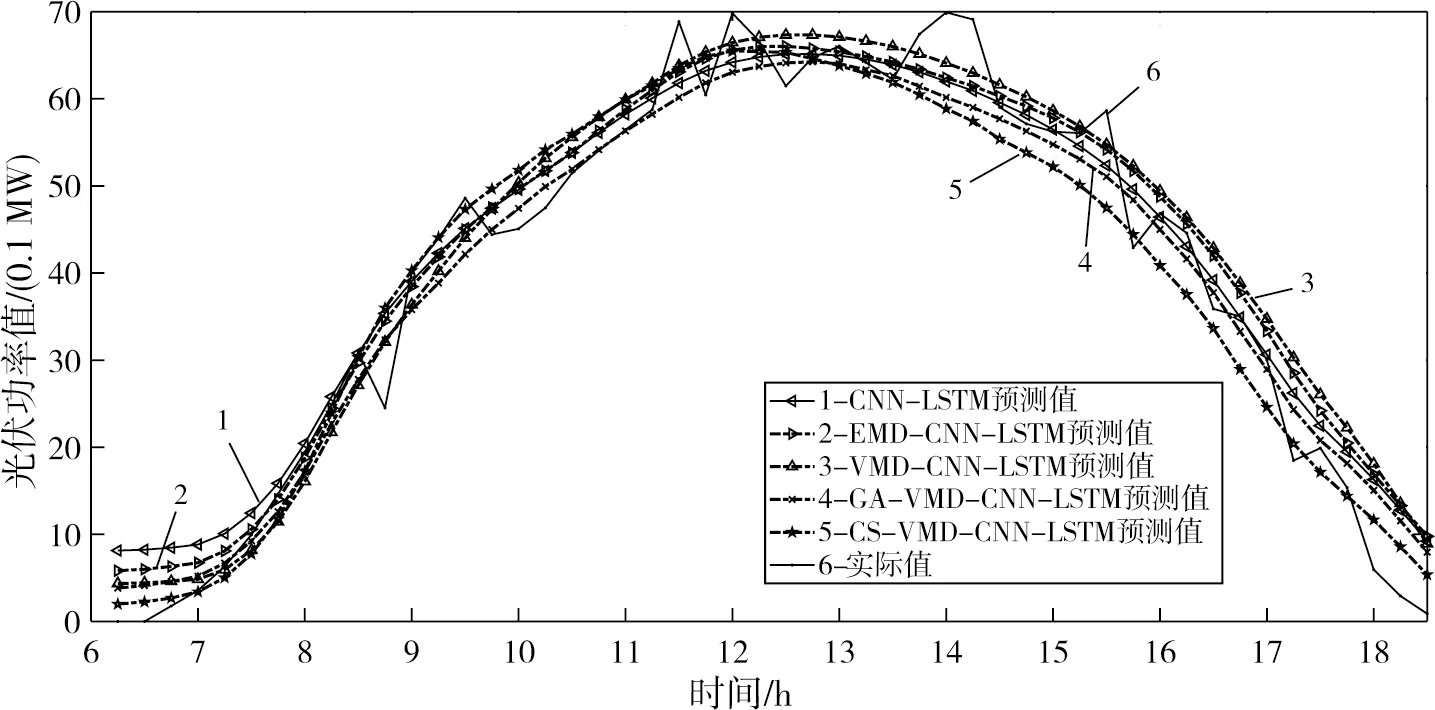
图6 不同模型的预测结果对比

由表2各方法的误差指标比较可知，本文提出的组合预测算例的预测值精度最高。LSTM算例可以充分提取各光伏功率数据中的特征，但CNN-LSTM算例会胜于单一LSTM时序预测算例，因为LSTM数据序列上存在传递依赖问题，而CNN 没有序列上的前后依赖问题，可以高效地并行运算。基于VMD分解的CNN-LSTM算例较之基于EMD分解的CNN-LSTM组合预测算例的偏差指数EMAE降低了15 kW，但指数ERMSE却上升了21 kW,两者预测性能不分伯仲，但基于上述单一分解算法易导致两端分散与模态混叠的局面。虽然VMD能够选择模态分量数，但需介入人为判断。而采用CS和GA优化算法自适应优化VMD参数的预测精度较为提升，与相同预测类型的GA-VMD-CNN-LSTM模型相比，本文方法的ERMSE和EMAE指标均大幅降低了73 kW和48 kW，因为GA优化过程中存在局部搜寻能力不足且不能省时，易导致过早收敛等问题。综合证明本文所提出模型的稳定性以及在光伏功率预测方面的可行性，可以应用于非线性、非平稳的光伏功率曲线时序预测中。

4 结语

为提高光伏功率预测的准确性，本文提出了基于优化的VMD-CNN-LSTM组合预测模型，并得出以下结论：

1)对具非平稳性的光伏功率时序进行预测时，将历史功率数据进行模态分解。基于CS-VMD模型可以寻求最佳模态个数与惩罚因子参数，且较单一EMD、VMD分解方法更能防止中心频率混叠局面的出现，在准确性和稳定性方面优于同类型的GA优化VMD算法。

2)不同天气，不同季节的光照辐射波动和云团运动轨迹均不同，均影响了光伏功输出功率曲线，未来计划引进相似日理论，并以光伏日出力进行功率预测进一步提高预测精度。