复杂应力场中非圆形隧道应力解析解研究

董 鹏，安 学 旭，王 智 阳，胡 志 平，辛 国 庆

(1.陕西省引汉济渭工程建设有限公司，陕西 西安 710024； 2.长安大学 建筑工程学院，陕西 西安 710061；3.中铁十八局集团隧道工程有限公司，重庆 400707)

0 引 言

在中国“西部大开发”及“一带一路”背景下，地下隧道工程不断地向地球深部发展，所面临的应力场环境越来越复杂[1-2]。对于深埋隧道，围岩初始主应力场分布多类似于图1(a)情况，但当初始主应力场与隧道断面主轴非平行时，关于围岩应力分布规律方面的解析研究较少，亟需开展研究。

关于主应力场对隧道断面应力分布影响的解析研究，诸多学者进行了探索，并取得了大量成果。对于隧道断面形状简单的圆形隧道，Wang[3]、陈登国[4]、Gao等[5]分别采用弹塑性理论与复变函数理论，对静水应力场或非静水应力场中隧道围岩应力分布规律进行了研究。对于断面形状复杂的非圆形隧道，目前相关研究多基于复变函数理论。如吕爱钟与张路青[6]、陈子萌等[7]研究了双向应力场中马蹄形、倒U形、方形、六边形、梯形等复杂隧道断面围岩应力分布规律。Muskhelishvili等[8]力学著作中也给了相关研究成果。此外，Kargar[9]、Zhao[10]、姜学焱等[11]还通过复变函数理论中柯西积分方法及幂级数解法对水平和竖向主应力场下隧道围岩应力变化规律进行了研究。但上述研究中，没有考虑隧道支护对围岩应力的影响，对此，王子豪[12]、李岩松等[13]推导了带支护隧道围岩应力解析解，并分析了支护对围岩应力的影响。Lyu[14-15]考虑了支护延迟对隧道围岩应力的影响。施有志[16]、Ma等[17]还通过复变函数理论对平行双孔隧道围岩应力变化规律进行了研究。Lyu[18]、Cai等[19]将隧道应力分布规律用于隧道断面优化及稳定性分析。在此研究基础上，吕爱钟[20-21]、Wang等[22]又研究了正交异性材料中考虑支护与不考虑支护情况下任意隧道断面围岩应力变化规律。

上述研究丰富了复杂隧道断面围岩应力分布解析解方面的理论成果，但现有研究主要集中在隧道断面主轴与初始主应力场平行的情况(图1(b))，对于与初始主应力场成一定角度的隧道断面围岩应力分布规律方面研究还存在空白，而实际地下隧道初始主应力场多类似于这种情况(图1(a))。对此，本文推导了一种考虑初始主应力场水平倾角的隧道围岩应力解析解，结合实际工程案例，研究了不同应力场工况下，主应力场剪切应力分量以及主应力场水平倾角改变对隧道围岩环向应力分布规律的影响。

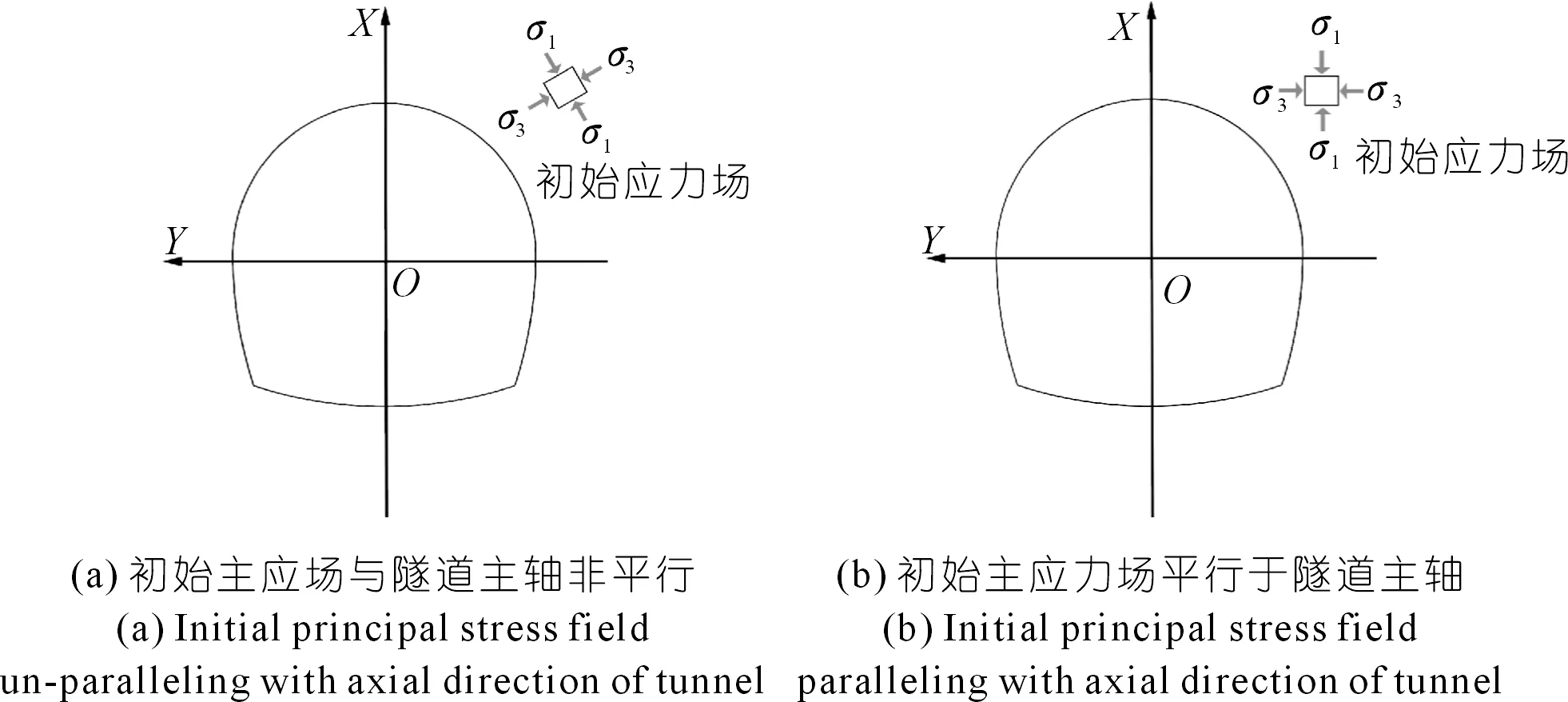
图1 非圆形隧道初始应力场示意

1 非圆形隧道应力基本方程

1.1 复应力函数求解

对于如图1所示隧道初始主应力场，可通过公式(1)分解为如图2所示的力学计算模型。

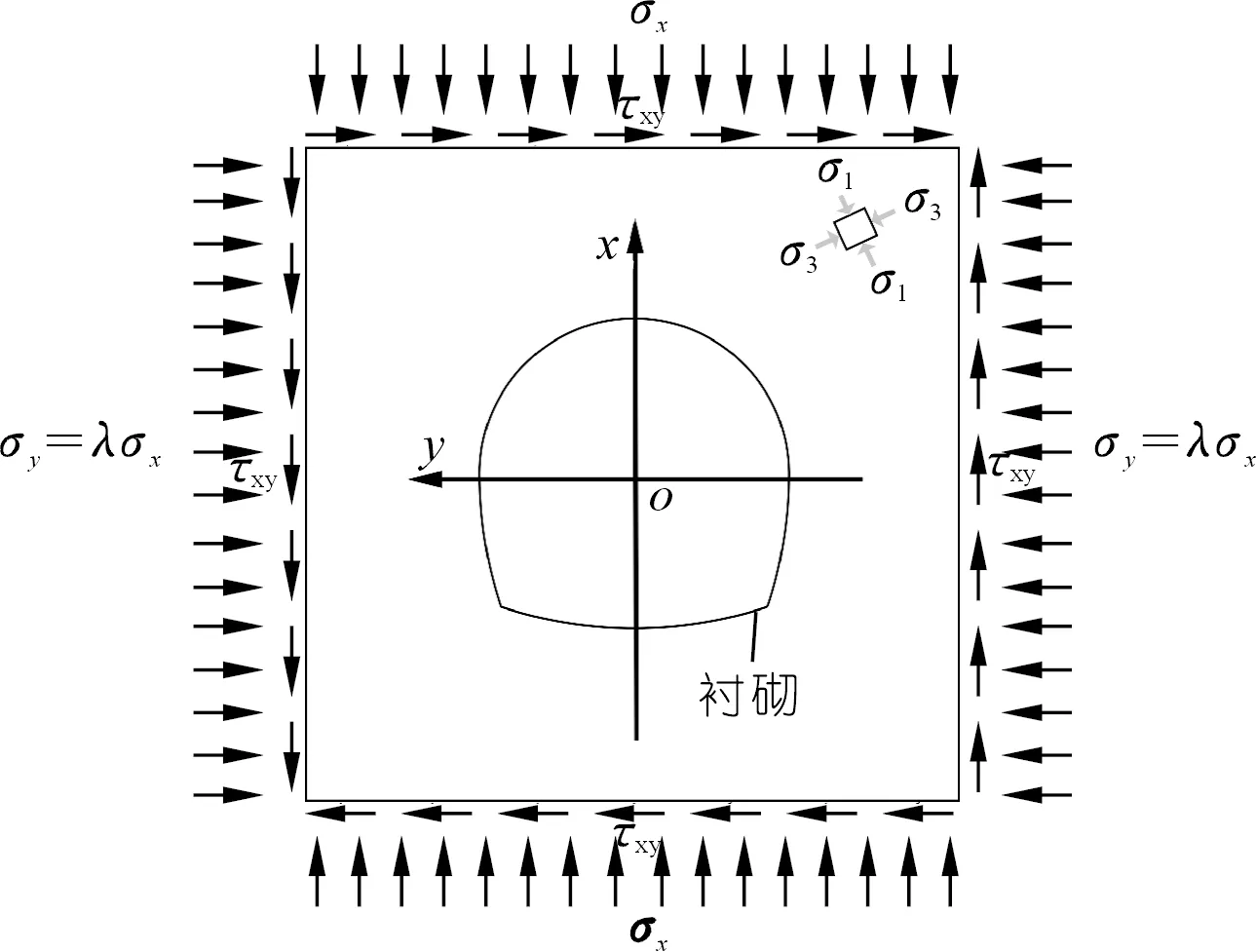
图2 非圆形隧道力学计算模型

(1)

式中：α为主应力场水平倾角；σy为主应力场水平分量；σx为主应力场竖向分量；τxy为主应力场剪切分量。

对于单连通域内任意断面形式L1，可通过保角映射转换为单位圆L2外域(图3)，其映射函数可用公式(2)表示。由于实际地下隧道断面形状的确定过程需要考虑施工难易程度及实用性等要求，断面多为几何形状相对规则的形状，且基本都关于竖轴对称。为了便于求解断面映射函数，通常选择竖轴为实轴，水平轴为虚轴，在此坐标系下断面映射函数系数ck是常实数。

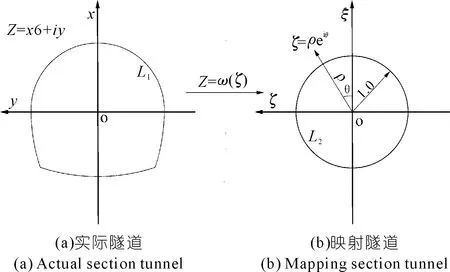
图3 实际隧道断面与映射隧道断面

(2)

式中：ω(ζ)为z平面上隧道断面形状的外部区域转换到ζ平面单位圆外部区域的映射函数；R为反映隧道断面大小的实数；ck为反映隧道形状的系数。

由隧道力学计算模型可知，求围岩应力解所需的两个解析函数可写成：

φ1(ζ)=Γω(ζ)+φo(ζ)

(3)

ψ1(ζ)=(Γ′+iτxy)ω(ζ)+ψo(ζ)

(4)

式中：φo(ζ)，ψo(ζ)可表示为

(5)

(6)

(7)

式中：Г1=σx(1+λ)/4，Г2=σx(λ-1)/2，λ=σx/σy。

(8)

当n≥3时式(8)右边第一项系数Lk为

(9)

由于φo(ζ)是圆外解析函数，因此可以表示为

(10)

模型边界条件中存在非对称剪应力分量，因此，式(10)解析函数φo(ζ)中系数ɑk一定是复数。

ak=ak1+i×ak2

(11)

应用式(8)和式(10)的左边项可构造式(12)：

(12)

当n≥3时，式(12)右边第一项sk系数为

(13)

将公式(12)和公式(7)代入公式(5)右边项，并分别进行柯西积分可得：

(14)

(15)

将公式(14)、(15)、(10)代入公式(5)，通过比较两边关于ζ-k各同幂次项系数，然后整理可得如下矩阵方程：

Xijaj=Ei(i，j=1，2，…，n-2)

(16)

当i=j时，公式(16)中系数Xij=jLi+j+1，若i+j+1>n时，Xij=0；当i≠j时，公式(16)中系数Xij=jL2i+1-1，若i+j+1>n时Xij=-1；公式(16)中右边项Ei可表示为

(17)

将公式(17)及各系数Xij代入公式(16)，可求出复系数ak(k=1，…，n-2)的实部与虚部值，其中an=-2Г1cn，an-1=-2Г1cn-1。然后将ak(k=1，2，…，n)值分别代入公式(10)和公式(13)即可获得圆外解析函数φo(ζ)及sk(k=1，2，…，n-2)值。

对公式(12)共轭，然后进行柯西积分可得：

(18)

对公式(7)共轭，然后进行柯西积分可得：

(19)

将公式(18)、(19)代入公式(6)可求出解析函数ψo(ζ)为

(20)

将公式(20)、(10)分别再代入公式(3)和(4)，可得两个复应力解析函数为：

(21)

(22)

1.2 围岩应力解

极坐标下隧道围岩任意点处的应力分量可通过式(23)、(24)获得：

(23)

(24)

由公式(23)、(24)可知围岩中应力解为

(25)

(26)

(27)

式中：Im()和Re()是对某复数取虚部和实部，σθ、σρ、τρθ分别隧道围岩环向、径向及剪切应力。

上述理论解在Matlab中通过编程即可求解，程序代码见附录。

2 主应力场对隧道应力的影响

2.1 工程概况及断面映射函数

引汉济渭工程是陕西省境内解决渭河流域缺水问题的重大引调水基础设施项目。秦岭输水隧道全长98.3 km，其中秦岭岭北TBM段隧道围岩具有大埋深(最大埋深可达2 012 m)、高地应力、高强度(平均单轴抗压强度为170 MPa)等特点，隧道开挖过程中引发了诸如岩爆、大变形、岩体剥落、掉块等工程灾变问题。为了进行隧道断面支护设计，在岭北6号实验洞附近采用三维水压致裂法进行了地应力测试，测试结果见表1[23]。隧道断面采用圆拱直墙和圆形两种形式，本文以圆拱直墙为例(见图4)，通过采用复合形优化算法，目标函数误差为0.043 9 mm，所求的隧道断面映射函数见公式(28)。为了便于分析，文中应力符号做如下规定，压为正，拉为负，后续围岩应力中正号表示压应力，负号表示拉应力。

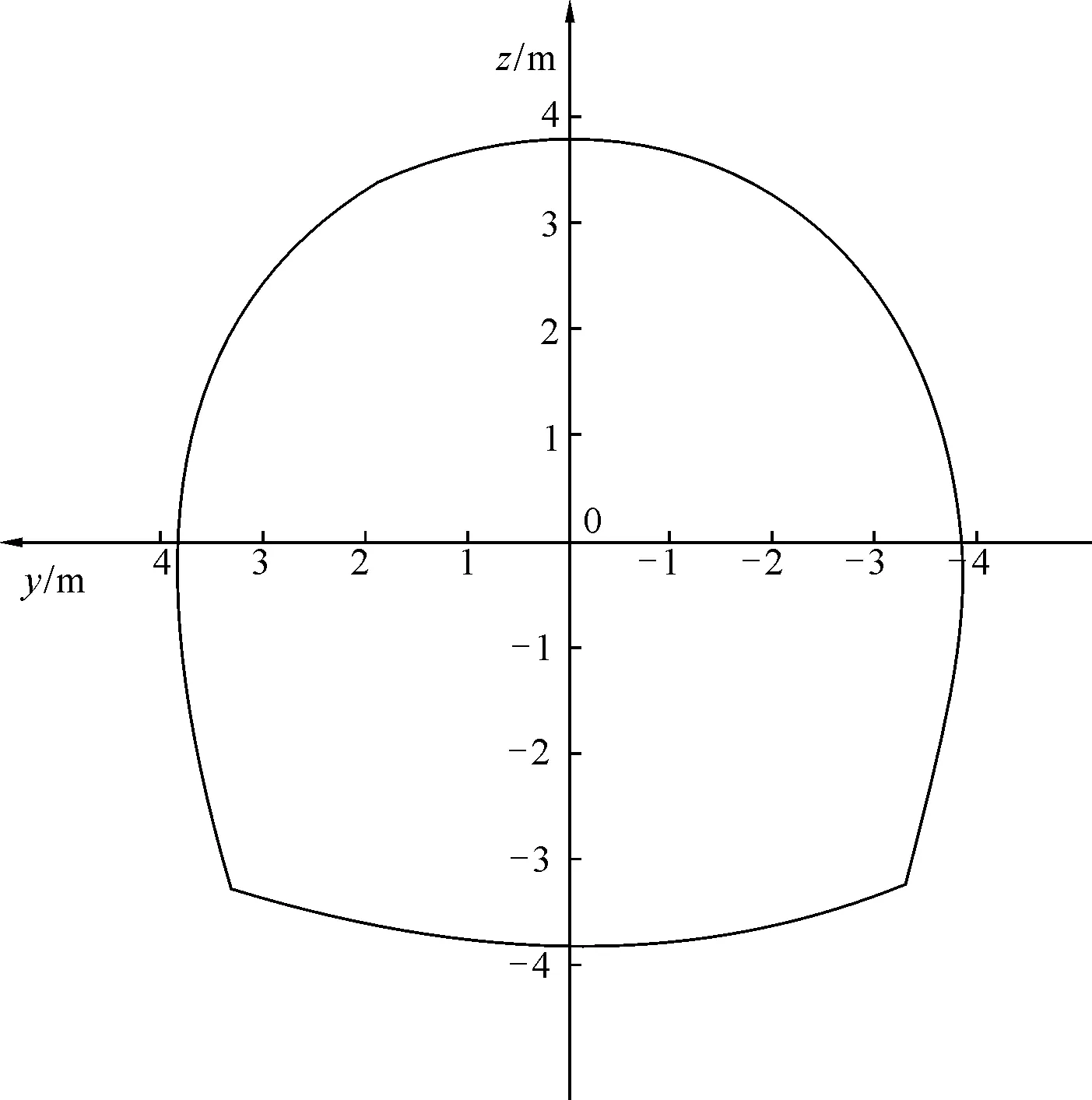
图4 引汉济渭工程非圆形隧道断面形状

表1 6号试验洞地应力测试结果[23]

z=ω(ζ)=3.98377(ζ-0.0519+0.0017ζ-1+

0.0391ζ-2-0.0422ζ-3+0.0229ζ-4-

0.0011ζ-5-0.0071ζ-6) (28)

2.2 主应力场剪切分量的影响

为了探究初始主应力场剪切分量对隧道开挖断面围岩应力分布规律的影响，根据2.1节围岩应力场参数及隧道断面映射函数，采用第一节中非圆形隧道解析理论，通过Matlab编程可分别获得考虑初始主应力场剪切分量(τyz=4.6 MPa)与不考虑初始主应力场剪切分量(τyz=0)时隧道环向应力σθ变化曲线(见图5)。

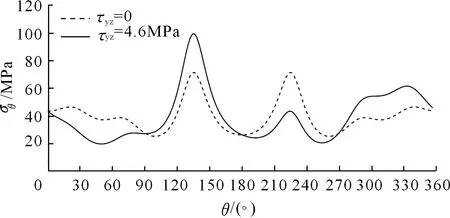
注：极坐标角度是从Z正轴逆时针开始。

由图5可知，考虑围岩初始主应力场剪切分量与不考虑围岩初始主应力场剪切分量时隧道环向应力曲线变化较大。在隧道0°～90°、180°～270°范围内，考虑初始主应力场剪切分量比不考虑时隧道环向应力小，二者最大差值处的比值为0.61；在隧道90°～180°、270°～360°范围内，考虑初始主应力场剪切分量比不考虑时隧道环向应力大，二者最大差值处的比值为1.39。由此可见，隧道初始主应力场剪切分量对隧道环向应力大小影响较大，实际工程中宜考虑主应力剪切分量对隧道断面围岩应力的影响。

从图5分析可知初始主应力场剪切分量对隧道环向应力影响较大，为了进一步探究主应力场剪切分量大小对隧道环向应力的影响，不考虑初始主应力场竖向及水平分量，通过分别改变主应力场剪切力分量大小(τyz=1.0，2.0，3.0，4.0 MPa)，采用解析理论，通过Matlab编程可求得随初始主应力场剪应力分量变化的围岩环向应力变化曲线(见图6)。

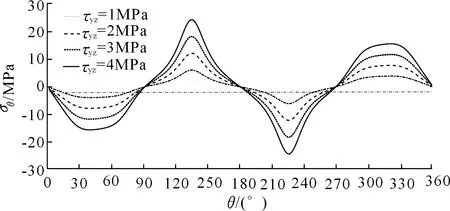
图6 不同τyz时隧道边缘σθ变化曲线

由图6可知，初始主应力场剪切分量对隧道开挖断面处环向应力大小影响显著。随着初始主应力场剪切分量的增大，隧道环向应力曲线的变化幅度整体在增大；不同工况下，剪切应力分量引起的隧道环向应力集中主要分布在30°～60°(左拱肩)、120°～150°(左拱脚)、210°～240°(右拱脚)、300°～330°(右拱肩)方位，且最大环向应力为相应剪切应力分量的6倍，并且在30°～60°与210°～240°方位，隧道围岩中会产生环向拉应力集中现象，尤其210°～240°方位环向拉应力较显著。由于围岩是抗拉强度较低的材料，因此在隧道施工过程需要格外的关注环向拉应力集中的位置，以免造成围岩受拉失稳破坏。

2.3 主应力场水平倾角的影响

为了探究隧道初始主应力场水平倾角对其围岩应力分布规律的影响，结合2.1节应力参数，设置了如表2所列的模型3种应力边界工况。

采用2.1节隧道断面映射函数，将表2中不同应力边界工况代入第一节隧道解析理论，求得随主应力场水平倾角α变化的隧道围岩环向应力变化曲线图(见图7)与环向应力场集中程度σθ/σ1变化曲线(见图8)。

图8 不同α时隧道边缘σθ/σ1变化曲线

表2 力学计算模型不同应力边界参数

由图7可知，初始主应力场水平倾角对隧道环向应力分布规律的影响呈现以下变化特征：

(1)随着主应力场水平倾角逐渐增大，隧道环向应力曲线除270°～330°范围外整体发生向左移动现象，说明主应力场水平倾角的变化会引起隧道围岩应力绕隧道边缘发生旋转。

(2)随着主应力场水平倾角逐渐增大，隧道120°～150°、270°～330°范围内的环向应力在升高，而隧道0°～60°、180°～240°范围内的环向应力却在降低，说明主应力场水平倾角变化会改变隧道围岩应力集中程度。

由图8可知，相对最大主应力场σ1而言，隧道120°～150°、210°～240°范围环向应力集中较大，最大可达3.7倍的最大主应力场。随着主应力场水平倾角的增大，隧道120°～150°、270°～330°范围的环向应力集中程度在逐渐增大，而隧道0°～60°、180°～240°范围环向应力集中在逐渐减小，由此可见，主应力场水平倾角的变化对隧道围岩应力集中程度具有显著影响。

3 结 论

(1)隧道主应力场剪切分量对马蹄形隧道环向应力影响显著。相同隧道断面考虑初始主应力场剪切分量与不考虑相比，二者隧道环向应力在左右拱脚处最大比值分别为1.39和0.61。

(2)初始主应力场剪切分量越大，隧道拱脚及拱肩处环向拉压应力越大，且最大值为相应剪切应力分量的6倍。

(3)主应力场水平倾角变化会引起隧道围岩环向应力绕隧道边缘发生旋转，从而造成隧道围岩环向应力集中分布区域的转移。

(4)随着主应力场水平倾角增大，隧道左拱脚及右拱肩处环向应力集中程度在增大，尤其左拱脚，最大可达3.7倍最大初始主应力，而隧道右拱脚及左拱肩处环向应力集中程度在逐渐降低。