2021年新高考数学I卷第20题学生答题分析与教学思考

赵雪鹏 (西安交通大学苏州附属中学 215028)

2021年新高考数学I卷第20题是一道立体几何题，难度适中，属于常规题.最近笔者所带的两个班级(高二年级比较好的两个理科班，学生的理解能力和运算能力较好)已经学完了空间向量这一章节，在复习课上，限时15分钟在这两个班级做了本道试题.但是学生普遍做得不理想，不少学生得分低，出现了很多出乎意料的错误.通过对学生答题情况进行细致的分析，笔者对学生的常见错误进行了归纳总结，并提出了若干想法.

1 试题赏析

(2021年全国新高考I卷第20题)如图1，在三棱锥A-BCD中，平面ABD⊥平面BCD，AB=AD，O为BD的中点.

图1

(1)证明：OA⊥CD；

(2)若△OCD是边长为1的等边三角形，点E在棱AD上，DE=2EA，且二面角E-BC-D的大小为45°，求三棱锥A-BCD的体积.

本题是一道立体几何题，以常见的三棱锥为模型，主要考查了面面垂直的性质定理、二面角及三棱锥的体积运算，试题背景常见，而且问题呈现的形式也比较常规，主要指向对空间几何的立体感及数学运算、直观想象、逻辑推理等数学核心素养.

2 学生答题情况

2.1 第(1)题答题情况

第(1)题主要考查面面垂直的性质定理，指向学生的空间立体感及逻辑推理能力.该题的常规做法是通过面面垂直的性质定理得到线面垂直，然后再通过线面垂直的性质定理得到线线垂直.具体做法如下：因为AB=AD，O为BD中点，所以AO⊥BD.因为平面ABD∩平面BCD=BD，平面ABD⊥平面BCD，AO⊂平面ABD，因此AO⊥平面BCD.因为CD⊂平面BCD，所以AO⊥CD.

第(1)题属于容易题，学生应该能做出来，但从批改的情况来看，该小题还是出现了以下一些典型的错误：

(1)在用面面垂直和线面垂直的性质定理时漏条件.在用面面垂直的性质定理时，很多学生漏掉了平面ABD∩平面BCD=BD和AO⊂平面ABD这两个条件；在用线面垂直的性质定理时，很多学生漏掉了CD⊂平面BCD这一条件.更有甚者，没有出现AO⊥BD和平面ABD⊥平面BCD这一关键条件，导致不必要的丢分.

(2)审题不清.学生审题不细心，答题不细致，丢了一些冤枉分.例如，第(1)题证明OA⊥CD，但有些学生看成了OA⊥OC；同样，由面面垂直的性质定理应该得到OA⊥面BCD，但有些学生误写成OA⊥面ABD.诸如此类的低级错误比比皆是，因此而丢分，实在可惜.

(3)还有的学生由于不理解面面垂直这一条件，乱写一通.首先得到AO⊥BD，然后默认为AO⊥OC，紧接着由线面垂直的判定定理得到线面垂直，进而得到线线垂直，这样的学生还不占少数.这类情况凸显出学生对试题的不理解，没有领会命题意图，对已学知识的掌握还不够熟练.

从以上这几种典型的错误可以看出，学生对所学知识掌握得不扎实，没有做到理解性地学习.例如，犯第(1)种类型的错误的学生，不理解面面垂直的含义，只是机械性地去背面面垂直的性质定理的条件，根据艾宾浩斯遗忘曲线的规律，很快会忘记，所以在答题时漏这漏那.同样，对于第(3)种错误，受所给图形的误导，默认为OA⊥OC，这是典型的条理不清晰.

2.2 第(2)题答题情况

第(2)题主要考查二面角及三棱锥的体积，指向学生的直观想象和数学运算能力.学生主要有两种解法，一种是综合演绎法，一种是向量坐标法.具体解法如下：

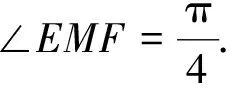
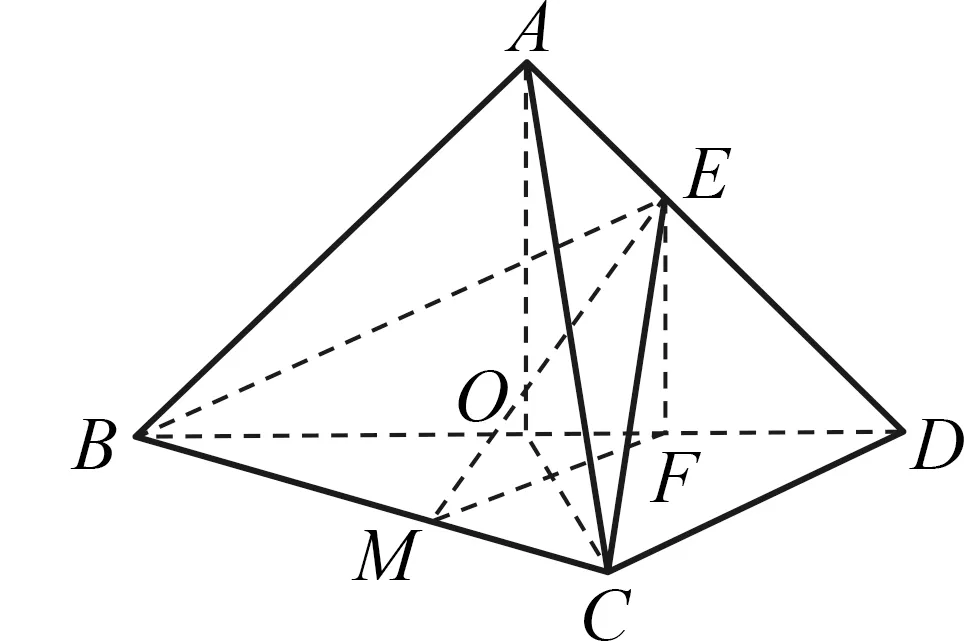
图2

方法2 (向量坐标法)第(2)题大部分学生使用向量坐标法，也是高中数学解决立体几何线面角和二面角等问题的常见方法.由于题中没有给出坐标系，要求学生自己先建系，每个人的建系有所不同，因此第(2)题的向量法解析不再陈述了，主要列举第(2)题解答中出现的一些问题.一些学生没有在解答过程中交代建系的过程，也没有在图中画出坐标系，作答过程极其随意；部分学生作答时缺乏逻辑性，例如，在求面EBC的法向量时，写出点E,B,C的坐标后，并没有接着写出向量EB,EC或BC的坐标形式，直接得到等式并求出法向量，导致解答过程不严谨；计算错误也是该方法中的一个常见问题，例如，部分学生写的方程组是对的，但法向量求错了，更有甚者，点C的坐标就求错了，导致本小题几乎不得分.诸如此类的错误让笔者感到触目惊心，本题本应是一道简单的送分题，硬被某些学生变成了“送命题”.因此，学生的学习方式急需调整.

3 教学建议

数学学科考试以数学基础知识为思维材料和操作对象，考查学生各方面已经得到发展的数学核心素养.在平时的教学过程中，教师要以数学的核心素养为导向进行有效的复习.

3.1 强化基础知识和基本方法

在平时的教学过程中，一定要以教材为依托，对照数学课程标准的学习要求，教学过程中稳扎稳打，讲透每一个知识点，切忌囫囵吞枣，不能让学生有云里雾里的感觉.对于一些重要的知识点，要反复强调，从最基础的题目抓起，通过题目强化学生对知识的理解.对于一些难度较大的题目，要引导学生从一些关键点上去打开缺口，引导优秀的学生自己去钻研，切不可过分提高要求.

对于数学中的一些基础知识和基本方法，记忆是一方面，更重要的是理解.俗话说“好记性不如烂笔头”，这句话稍微改编一下，变为“好记性不如知识理解”，那么学生的学习效果将更好.例如，学生在学习面面垂直的性质定理时，通过实物演示去理解这个过程，那么会更容易地记住这四个条件，无论过多长时间都能记住.因此，理解基础知识和基本方法显得尤为重要，也暗示着在平时的教学复习过程中不能一味地刷题，更要重视知识的形成过程.

同时，对于基础知识和基本方法的训练不应该只是简单的重复和片面的记忆，而要通过整理、归纳和总结，多方面地去认识每个数学知识及它们之间的联系.通过分类、整理，逐步形成一个条理化、有序化、网络化的知识结构体系，以便在解题时，准确依据给定的信息，快速寻求解题途径，优化答题过程，最终在考试过程中对基础知识的理解和基本方法的运用胸有成竹[1].

3.2 注意解题的规范性与完整性

数学解题应包含审题、语言表达、作答规范三个方面.

·审题规范

认真审题对正确解题而言至关重要，审题是对试题进行分析、寻找有用信息以及探求正确的解题思路的过程.审题过程包括弄清楚题干条件及问题、分析题干条件和问题之间的关系、找出正确的解题方法等三部分.

(1)分析题干中的条件和问题

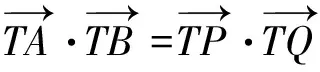
(2)分析条件与目标的联系

正确地解决一道试题，只分析条件或问题是远远不够的，常常需要将条件和问题联系在一起，寻找二者之间的内在联系，进而去联想与其相关的必备知识，逐一尝试，即可顺利解决本题.例如，2021年新高考I卷第19题，如果学生将题干的三等分点和问题结合在一起分析，就能想到互为补角的两个角的余弦值互为相反数，那么就会想到在两个三角形中对这两个角分别用余弦定理，可以得到三角形边的等式关系，进而解决本题.

(3)确定解题思路

一道试题的条件与问题之间必然存在着一系列的关联，这些联系是顺利解题的关键.然而用哪些关联去解题，需要根据这些联系背后的数学知识和其所遵循的数学原理来确定.对某些题目而言，这种联系比较隐蔽，只有通过认真的分析才能发现；而有些试题的条件和问题之间的联系有多种，这也是一题多解的原因所在[1].

·语言叙述规范

数学作为一门理科学科，有其严谨性和条理性.因此，教师在平时的教学(特别是新授课的教学)和学生在平时的学习中要板书清晰和答题规范，不可随意漏步骤和答题混乱.平时的阅卷过程中要看语言叙述是否到位.因此，学生的答题步骤应清楚、正确、完整，详略得当，言必有据.

·作答规范

进入高中，考试对于学生而言是再正常不过的事情，但是一到考试，学生多少会有点紧张，这时很容易犯一些低级的错误，而自己还不自知.例如，在本道试题第(1)题证明中学生所犯的错误.学生的作答要准确、简洁、全面，既要注意结果的验证、取舍，又要注意答案的完整，要做到审清题目的目标，按目标作答.

3.3 提高学生的计算能力

数学运算作为数学六大核心素养之一，渗透在数学考卷的各个方面.现在的数学考试主要考学生的“想”和“算”，而“算”的准确性是学生能拿到基本分的关键，显得尤为重要.本道试题的第(2)题，用向量法做题时，有的学生一开始就把点C的坐标求错，往下的过程虽然全对，但一分不得，这样的错误非常可惜.因此，提高学生的数学运算能力显得尤为重要.要想提高运算能力，一方面需要通过限时的练习来提高做基础题的速度，另一方面要提高运算的准确率.提高运算能力不仅要细心，更需要思考，且“思”要在“算”的前面.通过思考，明确运算的方向，能对运算的结果有一定的预见性.平时的教学过程中一定要重视学生的计算，涉及到计算问题，例如概率统计、空间向量求二面角和解析几何等计算量大的题目，务必让学生去算，甚至课堂上专门拿出时间让学生去做，这是划得来的.通过比较不同的算法，提高数学运算的速度和准确率.

3.4 注意答题细节，养成好的答题习惯

平常数学考试的阅卷过程中经常反馈出来的信息是：难题大家几乎都拿不到分，而简单题、送分题也有很多人得不到分.究其原因，主要是答题习惯差、书写不注意细节.

对于学生做题过程中的主要问题，笔者作了如下的梳理，以备今后教学中注意.

(1)字不必要漂亮，但必须清晰有条理

平时教学中，有教师强调卷面整洁、字体漂亮可以赢得阅卷老师好感，多得分.于是有的学生便刻意而为，字体力求漂亮.其实，在考试紧张的状态下，过分关注字体漂亮，势必会影响答题的速度.因此，遵循“慢思考、快答卷、字迹清”才是更可行的准则.所以，字不必要漂亮，但要一目了然，答题过程要清晰有条理.

(2)答题过程不必要详细，但要突出重点步骤，尽可能覆盖“得分点”

任何考试的阅卷基本原则之一是“看点给分”，这就要求考生能尽量清晰有条理地把必要的知识点、关键步骤写出来.在阅卷过程中，不少学生不着边际地乱写一通，但没有得分点，因此劳而无功，白白浪费了宝贵的时间.

在平时的学习过程中，教师和学生要经常性地反思自己的教学和学习方式，在反思过程中，不断地对自己不合理的教学和学习行为进行批判，督促自己不断地学习进步，成就最好的自己.