Apple grading method based on neural network with ordered partitions and evidential ensemble learning
Liyao Ma|Peng Wei|Xinhua Qu|Shuhui Bi|Yuan Zhou|Tao Shen
1School of Electrical Engineering,University of Jinan,Jinan,China
2Blekinge Institute of Technology,Karlskrona,Sweden
Abstract In order to improve the performance of the automatic apple grading and sorting system,in this paper,an ensemble model of ordinal classification based on neural network with ordered partitions and Dempster–Shafer theory is proposed.As a non‐destructive grading method,apples are graded into three grades based on the Soluble Solids Content value,with features extracted from the preprocessed near‐infrared spectrum of apple serving as model inputs.Considering the uncertainty in grading labels,mass generation approach and evidential encoding scheme for ordinal label are proposed,with uncertainty handled within the framework of Dempster–Shafer theory.Constructing neural network with ordered partitions as the base learner,the learning procedure of the Bagging‐based ensemble model is detailed.Experiments on Yantai Red Fuji apples demonstrate the satisfactory grading performances of proposed evidential ensemble model for ordinal classification.
KEYWORDS apple grading,Demspter–Shafer theory,ensemble learning,ordinal classification
1|INTRODUCTION
Apple is one of the most significant fruits in our daily life due to its good taste,rich nutrient content and convenient preservation.Owning abundant land resources with suitable climate and sunlight,China has become the largest apple producers in the world[1].As an essential step in post‐harvest management,apple grading helps to upgrade the value‐added capability and strengthen the competitiveness of domestic apples.Meanwhile,it is also conducive to standardised operations in apple production and distribution.The traditional manual apple grading has great limitations,such as(1)long working time leads to mistakes and low efficiency,(2)the grading results may differ due to workers'divergent understandings of the grading standards and(3)it is difficult for workers to grade apples with internal qualities that cannot be observed by eyes.
With the development of artificial intelligence technology and sensor technology,machine learning algorithms are gradually applied to automatic apple grading.To predict the apple grades non‐destructively,image[2,3]and near‐infrared spectrum[4,5]are often used.Yang et al.proposed to extract features from multiple images and classify apples by weighted k‐means algorithm[6].Li et al.used size,colour and fruit shape of apples as features and combined multiple BP neural network classifiers to make a final prediction[7].Based on the image acquisition system,Yu et al.proposed to classify apples with colour features,achieving an accuracy of 89%[8].In Ref.[9],Shan et al.combined hyper‐spectral imaging technology and spectral analysis technology to realise the detection of early damage on the apple surface and the prediction of apple SSC.Xi et al.estimated the SSC values of apples based on near‐infrared spectrometer and partial least squares method,and improved the accuracy and efficiency through a multi‐region combination method[10].Authors of this paper also have applied evidential classification forest[11]and multi‐model fusion[12]to solve the apple grading problem.However,without considering the ordinal nature of grading labels,all the existing methods treated apple grading as a traditional classification problem,resulting in insufficient information utilisation.
From the view of machine learning,apple grading is actually a problem of ordinal classification[13](also known as ordinal regression).It is a special kind of supervised learning approach,with consideration of the ordinal variables appeared in various practical problems,such as the apple grades1st grade≻2nd grade≻3rd gradein this paper.Since there are natural ordering relations among labels,it differs from classification and regression.In recent decades,various ordinal classification methods have been proposed by considering ordered labels within classification models,such as incremental learning model[14],support vector machine[15,16],deep learning model[17,18]and so on[19–21].Now ordinal classification has been widely used in many fields such as pain assessment[22],consumer preference[23],medical research[24]and diagnostic system[25].We have used neural network with ordered partitions(NNOP)[26]and support vector ordered regression[27]in apple grading problem1This paper is a revised and extended version of the short paper[26]presented at the ICAMechS conference,Japan,2021..However,actually little research has been done to grade fruits by the ordinal classification model as it is not familiar to researchers in the agricultural area.
In this paper,grading performance of previously used NNOP ordinal classification model[26]is improved:The single NNOP model is adopted as the base learner and extended to the ensemble case;meanwhile,epistemic uncertainty in ordinal grading labels is now considered and handled by Dempster–Shafer theory[28,29],which has the ability to express a variety of states of knowledge,ranging from full information to complete ignorance.Apples are graded according to Soluble Solids Content(SSC),an important indicator of apple's internal quality.Motivated by the decision‐making criterion in partial classification[30],an evidential ordinal encoding scheme is proposed to take better advantage of SSC information.The main contributions of this paper includes as follows:(1)Taking data uncertainty into consideration,the mass generation approach and evidential encoding scheme for apple grading are designed;(2)a Bagging‐based evidential ensemble model with NNOP as base learners is proposed for ordinal classification;(3)the evidential ensemble grading algorithm providing good performance for automatic non‐destructive grading of Red Fuji apples is studied and verified.
The rest of this paper is organised as follows:Section 2 introduces the data collecting and preprocessing for apple grading task.Section 3 is devoted to the construction of proposed evidential ensemble model,especially the evidential encoding scheme,base learner establishment and the ensemble details.Section 4 demonstrates the performance of ensemble model with experiments performed on Red Fuji apples.Finally,the main conclusions are summarised in Section 5.
2|APPLE DATA COLLECTING AND PREPROCESSING
In this paper,apple grading is implemented with the automatic apple grading and sorting system developed by our research team.As shown in Figure 1,for each apple instance,as it moves on the conveyor belt,its near‐infrared spectrum is collected and the apple is graded non‐destructively by the proposed evidential ensemble model of ordinal classification.In the end,the apple instance is sent to the corresponding sorting basket for storage.
The apple grading model,which maps the near‐infrared spectral information of an apple to its grading label,is constructed by the proposed learning approach.The naturally ordered grading label is judged by SSC,which is a key indicator of apple's internal quality.To train and test the learning model,we first introduce the data collecting and preprocessing procedures and generate the datasets used for later discussion.Red Fuji apples produced in Qixia,Yantai were adopted for the grading analysis.A total number of 439 apples with uniformed colour and no obvious external defect were used as instances for model training and testing.All apples had the diameters ranging from 76.0 to 84.5 mm,with mean of 80.5 mm and standard deviation of 3.3 mm.The storage environment of all apple instances before data collection was set at the temperature of 26°C and the humidity of 64%.
Originally,the near‐infrared spectrum and corresponding SSC value were collected for each apple instance,as shown in Figure 2.Using the Fourier transform near‐infrared spectrometer in Figure 2a,we achieved the near‐infrared spectrum,with the wavelength ranging within 4000~10,000 cm−1and the resolution being 8.0 cm−1.Three points were picked equidistantly from the surface of the apple equatorial plane for spectrum collection.The spectral data of the three points were averaged to obtain the final spectrum for this instance.The SSC value of the instance is obtained by physical and chemical experimental methods.Being destructive,a small portion of the apple instance was squeezed by knife,placed in a mortar and mashed into pieces,as shown in Figure 2b.The juice was taken by a rubber dropper into a refractometer to measure the SSC of the instance(Figure 2c).For SSC collection,equipment was washed and dried for each instance,avoiding influence on other measurements.

FIGURE 1 Equipment of the automatic apple grading and sorting system

FIGURE 2 Data collection for apple grading models.From left to right:(a)near‐infrared spectrum collection,(b)physical and chemical experimental process and(c)measurement of Soluble Solids Content
To train the ordinal classification model,the dataset should be generated based on previously collected data.The inputs of the model are features extracted from the apple spectrum.Figure 3 depicts the collected spectra for all 439 apple instances,withx‐axis the wavelength ranging from 4000 cm−1–10,000 cm−1,andy‐axis the corresponding absorbance.The spectra need to be preprocessed before feature extraction.In this paper,baseline drift was reduced by multivariate scattering correction,and the anomalous instances were eliminated by principal component analysis combined with the Markovy distance method.In addition,the noise was filtered by the Savitzky–Golay convolutional smoothing method.In order to retain the valid information to the greatest extent,features of an apple instance were obtained as the first 30 principal components of its processed spectrum.The output of the instance is its grading labelyencoded according to its SSC value,as detailed in the next section.
3|ENSEMBLE LEARNING MODEL BASED ON NEURAL NETWORK WITH ORDERED PARTITIONS AND DEMPSTER–SHAFER THEORY
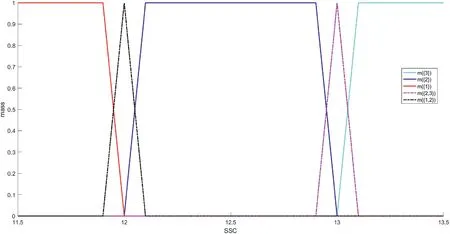
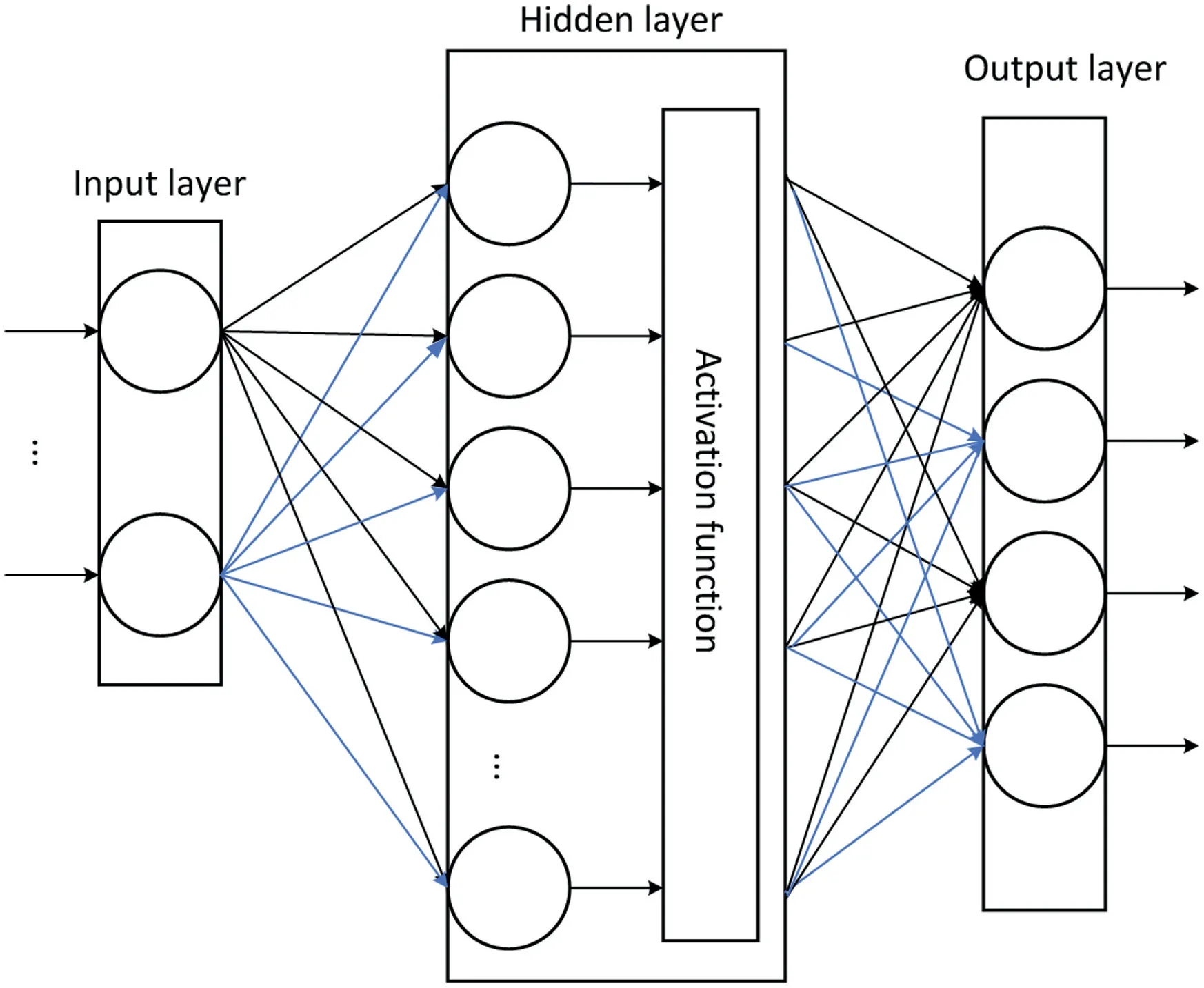
In this section,dealing with epistemic uncertainty by Dempster–Shafer theory,an ensemble learning model based on NNOP is proposed to implement apple grading.Following Section 2,we get the dataset that containsNinstances,withrepresenting the features of apple instanceiconsisting ofpattributes andyibeing its grading label taking value in the finite setY={1,2,…,K}with a strict order relationship 1<2<… FIGURE 3 Near‐infrared spectra for all apple instances Considering the ordering relation of grading labels,the traditional NNOP model works with target outputs in the formation of=[1,…1,0,…,0],where It comes from the idea that if an instance belongs to thek‐th grade,it is also classified into its lower‐order grades{1,2,…,k−1}.Gathering the target outputs of all possible grades together,the ordinal coding matrixis obtained as shown in Table 1.Theith column ofrepresents the encoded output ofith grade.The matrix elementrepresents the output coding bitcorresponding to output nodei,given gradej. Basically,a grading labelycan be decided depending on the SSC value as Here,the boundary 12 and 13 are specifically set according to the particular situation of used apple instances.All the apples with SSC value lower than 12 are set to be the third‐grade apples,while apples with SSC value greater than 13 set to be the first‐grade apples,and the rest the second‐grade ones.However,there is uncertainty within the SSC values,especially when the instances fall in the area near the grading boundaries,leading to misclassification.So in this paper,we take the uncertainty into consideration and propose the evidential encoding scheme based on~T. The epistemic uncertainty in grading labels is modelled and handled within the framework of Dempster–Shafer theory,which generalises both set and probabilistic uncertainty.Let the finite set K={1,2,…,K}be theframe of discernment,containing all the possible exclusive values that the grading label can take.When the true value of the label is ill‐known,we can model its partial information by amass function m:2K→[0,1]such thatm(∅)=0 and A subsetAof K withm(A)>0 is called afocal setofm.We can interpret the quantitym(A)as the amount of evidence indicates that the true value is specifically inAwhile in no strict subset.Considering the uncertainty in SSC values and grading labels,mass functions are generated for apple instances near the grading boundaries.Two focal sets are considered here,the singletonand the setSconsisting ofand its adjacent label.m()depicts the support degree of classifying this apple as grade,whilem(S)shows the amount of evidence indicating that the grade of apple falls in the set of adjacent labels.Given SSC valueys,mass assigned to this set is computed as TABLE 1 Ordinal coding matrix TABLE 1 Ordinal coding matrix Coding True grade Bits 1(III) 2(II) 3(I)~t1 1 1 1~t2 0 1 1~t3 0 0 1 For the instances near boundary 12,m({1,2})is calculated witha=11.9,b=12,c=12.1,while for the instances near boundary 13,m({2,3})is calculated witha=12.9,b=13,c=13.1.The rest of the mass is assigned to the singleton decided by Equation(2).For example,whenys=13.03,its mass function is detailed as which means that according to SSC valueys,we regard this instance as first‐grade with confidence degree of 0.3 and judge it as first‐grade or second‐grade(without any additional judgement)with confidence degree of 0.7.Figure 4 shows the mass assigned to the focal sets with different SSC values. The evidential encoding scheme is based on the ordinal coding matrixand mass functionmof the grading label,following the idea of generalised Maximax criterion in decision theory[31].To generate the evidential coding vectort=[t1,…,tK],each coding bittiis calculated by the upper expected coding value which means that when a focal setBis considered,the maximum coding value of elements in this set is selected.By the proposed encoding scheme,the SSC of an apple in the training set is transferred into a mass function describing its support degree on grading decision and then turned into the evidential coding vectortas the output of this apple instance. FIGURE 4 Mass function generation Now the base learner of NNOP model can be learnt from the training setInputs of an instancexi=arepfeatures extracted from the spectrum.The correspondingK‐bits target output is achieved by the evidential encoding scheme asti=[ti1,…,tiK],where the total coding bit is the same with the number of apple gradesK=|K|. As shown in Figure 5,the NNOP base learner has the structure of one model with multiple outputs,which is similar to the traditional neural network.The model consists of the input layer,the hidden layer and the output layer,with full connections among nodes in adjacent layers.To construct the NNOP model,the input layer transmits the features of spectrum to the hidden layer by multiplying them with weights.The hidden layer then delivers information to the output layer by activation function and weighting operation.With the square error cost function,the weights in the NNOP model are adjusted by back propagation.When the cost function achieves the minimum value,the NNOP model obtains the best training performance. The traditional neural network model is aimed at predicting the probability that an instancexibelongs to a classk,without considering the relation among labels.Therefore,its target vector is in the form oft=(0,…,0,1,0,…,0),with only thek‐th element being 1.One step further,the traditional NNOP model[32]considers the ordering relation of grading labels,with order‐encoded target vectort=(1,1,…,1,0,…,0),in whichti=1,1≤i≤kandti=0,k FIGURE 5 Structure of neural network with ordered partitions In addition,the activation function in the hidden layer of NNOP can still be chosen among the sigmoid function,the linear function,and thetanhfunction.Yet according to the characteristic of order‐encoded vector,activation function in the output layer must be sigmoid function rather than the softmax functionwhereziis the input of thei‐th output node.Weights within the model are tuned to make the output being as close to the given target vector as possible.To this end,the output error is first propagated forward to the output node,then propagated backward from the output layer to the hidden layer and finally to the input layer.In this paper,square error between the prediction vector and the target vector is selected as the cost function,which is detailed as Considering the sigmoid transfer function in the output nodes of NNOP,the derivation offtfor thei‐th output node is which leads to the result that the error propagated to output nodeOiis Once the NNOP model is established,to make a grading prediction for a new apple instance,inputting its spectral features,all the output nodes…of NNOP are scanned in order,until the value of one node falls below the predefined thresholdTor no node left for scanning.Finding the last node with an output greater than thresholdT,its labelkis then selected as the predicted grade of the instance. FIGURE 6 Overall structure of ensemble model learning Based on the evidential encoding scheme and NNOP model construction,the Bagging‐based evidential ensemble model is learnt.As depicted in Figure 6,given the training setTobtained from apple instances,a collection of new training subsets are sampled with replacement fromT,using the Bagging algorithm.For each training subset,an NNOP model is learnt separately as the base learner.The ensemble model treats each NNOP model equally and makes the final grading prediction by decision making of major voting. Algorithm 1 summarises the Bagging‐based evidential ensemble approach of NNOP.Once the evidential ensemble model is learnt,it can be used for grading of new apple instances.Given the features of a new apple instance,the prediction of its grading label is made by major voting of all predictions of NNOP base learners. Algorithm 1 Bagging-based evidential ensemble algorithm To validate the proposed evidential ensemble model of ordinal classification,experiments were carried out on 439 Red Fuji apples grown in Yantai,Shandong.Each apple instance was classified into one of three grades(first‐grade,second‐grade and third‐grade)based on the 30 features extracted from the spectrum by means of principal content analysis.Therefore,each NNOP base learner had the structure of 30 nodes in the input layer and 3 nodes in the output layer.The model was set to have one hidden layer,with activation functions in both the hidden layer and the output layer being sigmoid function. We first discuss the selection of several key parameters in the evidential ensemble model of ordinal classification.It should be noted that all the experimental results shown in Section 4.1 and 4.2 are the grading accuracies obtained on the test sets.To study the influence of model parameters,after eliminating 10 anomalous instances,286 randomly selected apple instances(2/3 of total number)were fixed as the training set,while the rest 143 instances were assigned to the test set.All experiments were repeated three times,with the averaged accuracy as the final result. The ensemble model was first set with the following parameters:number of nodes in the hidden layer of each NNOP modeln=60 and proportion of instance sampling in the Bagging algorithmp=1.The change of grading accuracy with varying number of base learnershis shown in Figure 7.Due to the random initialisation of NNOP weights and the random instance selection in the Bagging algorithm,the curve shows some volatility,which also occurs in the following experiments.Using a single NNOP model with evidential coding vector,the grading accuracy is around 90.3%.As number of base learners increases,the grading accuracy has an increasing trend whenhis relatively small and varies around 91.5% whenhis greater than 15.Basically whenhis larger than 15,the performance is somehow steady,so we seth=20 in the next experiment,with consideration that more base learners lead to more computational time. Seth=20 andp=1;Figure 8 depicts the changing grading accuracies when the NNOP model has different number of nodesnin the hidden layer.Still,volatility exists in the results.Generally,the accuracy varies between 91% and 91.7%.Accuracies of the ensemble models with relatively small number of hidden nodes(say,n∈[30,80])show a larger variance than those with more hidden nodes(such asn∈[80,120]).Considering the feature number of our apple data and the computational complexity of model,n=40 is selected. Let the ensemble model for ordinal classification have 20 base learners,each with 40 hidden nodes.The proportion of instance sampled for the sub‐training set in the Bagging algorithm is discussed.As shown in Figure 9,when the proportion is small,sayp=0.55,the sub‐training setTifor each NNOP model has a scale being only 55% of that of the training setT.With not enough information,the grading accuracy is quite low.Aspincreases,the grading accuracy of the ensemble model increases and exceeds 90%.The larger isp,the more training instances are contained in the sub‐training set,providing more information for model learning.As only several hundreds of instances are used in the experiment,not much computational load will be added even whenp=1.It is also remarkable that due to the data distribution and randomness within the ensemble model,only relatively satisfactory performances can be achieved with selected parameters,rather than the optimal performance. FIGURE 7 Grading accuracy with varying number of base learners FIGURE 8 Grading accuracy with varying number of hidden nodes In this section,to validate the performance of proposed approach,five‐fold cross validation was implemented with the 439 Red Fuji apple instances(among which 10 anomalous ones were eliminated).The grading performances of four models are compared: ·single NNOP model with ordered encoding scheme(S‐O); ·single NNOP model with evidential encoding scheme(S‐E); ·ensemble model with ordered encoding scheme(E‐O); ·ensemble model with evidential encoding scheme(E‐E). The evidential ensemble model was set to contain 20 NNOP base learners,each of which has 40 hidden nodes.When generating the sub‐training sets using the Bagging algorithm,each time a total number of 1*|T|instances were randomly selected from training setT(p=1).Grading accuracies on the test sets are shown in Table 2. Experiment on the Red Fuji apple dataset verifies the effectiveness of proposed approach.Since different data are used for training and testing in each cross validation,the grading accuracies of the same model differ.Basically,no matter which encoding scheme is used,the ensemble model has better performance than a single model.Thanks to the encoding scheme based on mass functions,the approaches with evidential encoded vectors can take better advantage of apple data,leading to higher accuracies than those with traditional order encoded vectors.The proposed ensemble model based on evidential encoding scheme and NNOP base learners can achieve the best performance in all the cross validations,with an averaged grading accuracy of 91.60%(the average of the five E‐E accuracies in Table 2). FIGURE 9 Grading accuracy with varying proportion of Bagging instance sampling To improve the performance of Red Fuji apple grading,a Bagging‐based evidential ensemble model of NNOP is proposed in this paper for ordinal classification.Considering the uncertainty in SSC values,within the framework of Dempster–Shafer theory,mass functions are generated to model the epistemic uncertainty in grading labels.On that basis,the evidential encoding scheme for ordinal label is designed.The training set is thus generated with features extracted from near‐infrared spectrum as inputs and evidential coding vectors as outputs.Following the idea of Bagging algorithm,multiple sub‐training sets are obtained by sampling with replacement from the training set.For each subset,an NNOP model is learnt as the base learner.Aggregating the grading decisions of all base learners by major voting,the ensemble model of ordinal classification provides grading predictions for new instances.With experimental validation,the proposed approach can achieve satisfactory grading performances on Red Fuji apples.It is worthwhile to note that although the proposed approach is designed on a special kind of apples,the evidential ensemble model can also be used for other fruit grading,with details of mass generation and parameter settings modified according to the characteristic of data.In the future work,models with higher grading accuracy will be considered as the base learner of evidential ensemble model.Also,we will discuss the evidential partition of apple instance space with more complicated decision‐making strategies. ACKNOWLEDGEMENTS This paper is supported by the Natural Science Foundation of Shandong Province ZR2021MF074,ZR2020KF027 and ZR2020MF067,and the National Key R & D Program of China 2018AAA0101703. CONFLICT OF INTEREST The authors declare that there is no conflict of interest. DATA AVAILABILITY STATEMENT The data that support the findings of this study are available from the corresponding author upon reasonable request. ORCID Shuhui Bihttps://orcid.org/0000-0002-2832-4985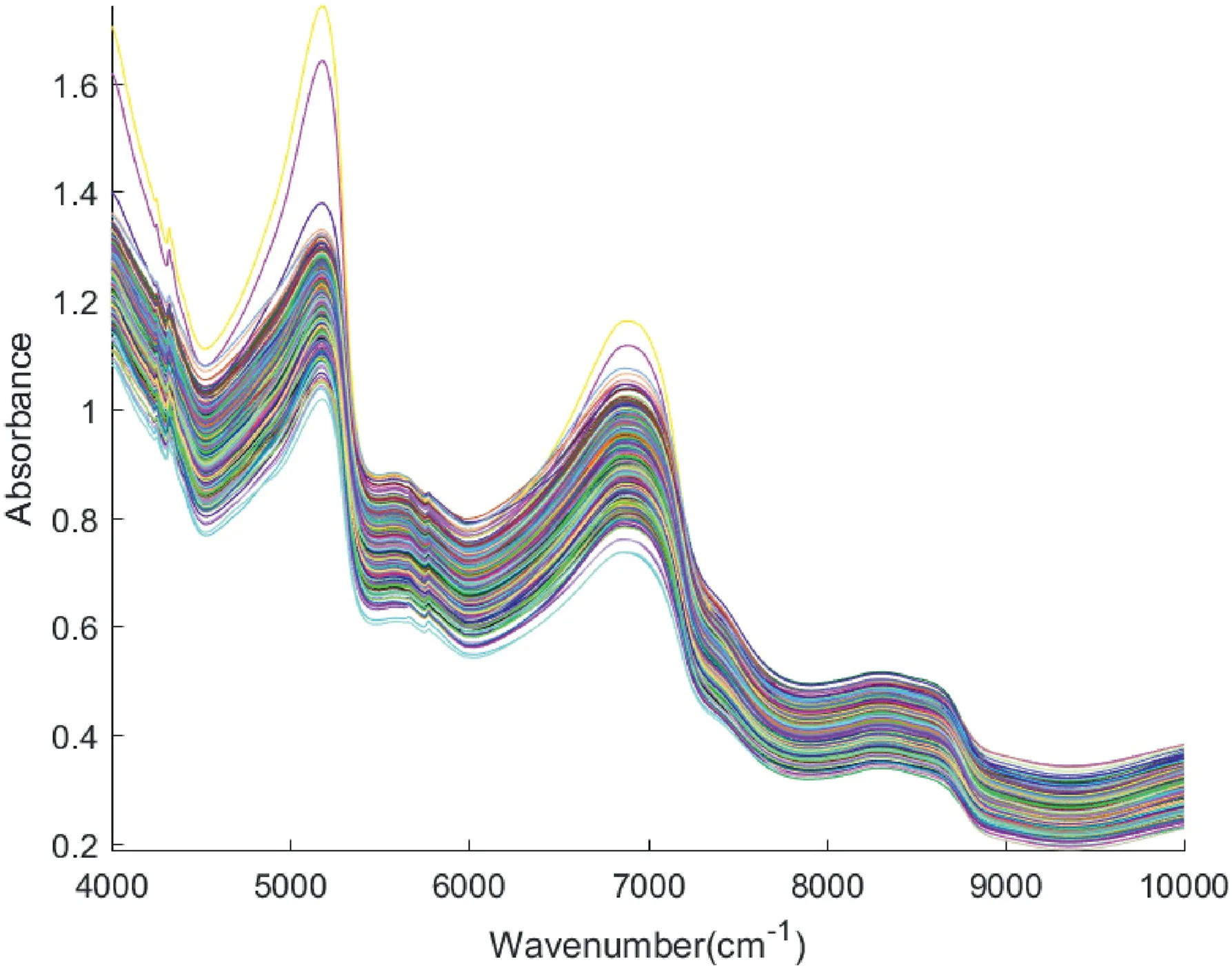
3.1|Evidential encoding scheme for ordinal labels
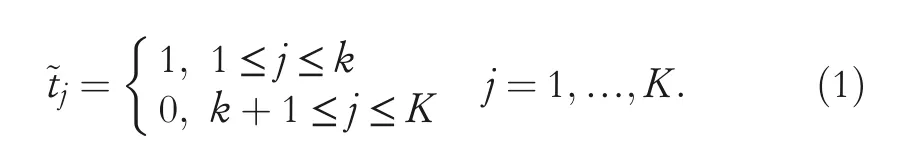

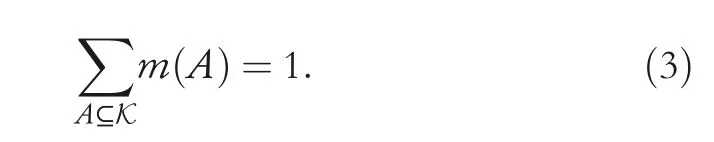




3.2|Construction of NNOP base learners



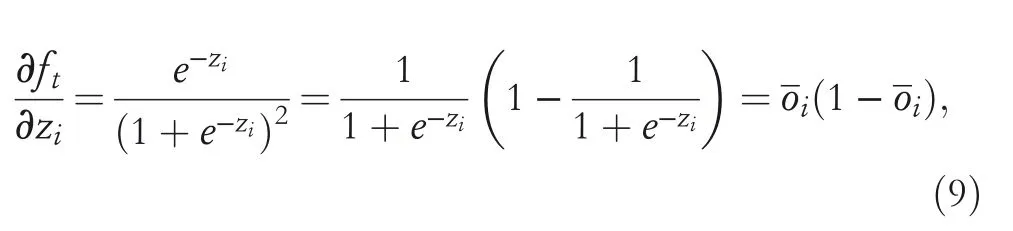


3.3|The ensemble model for ordinal classification

4|EXPERIMENTS ON RED FUJI APPLES
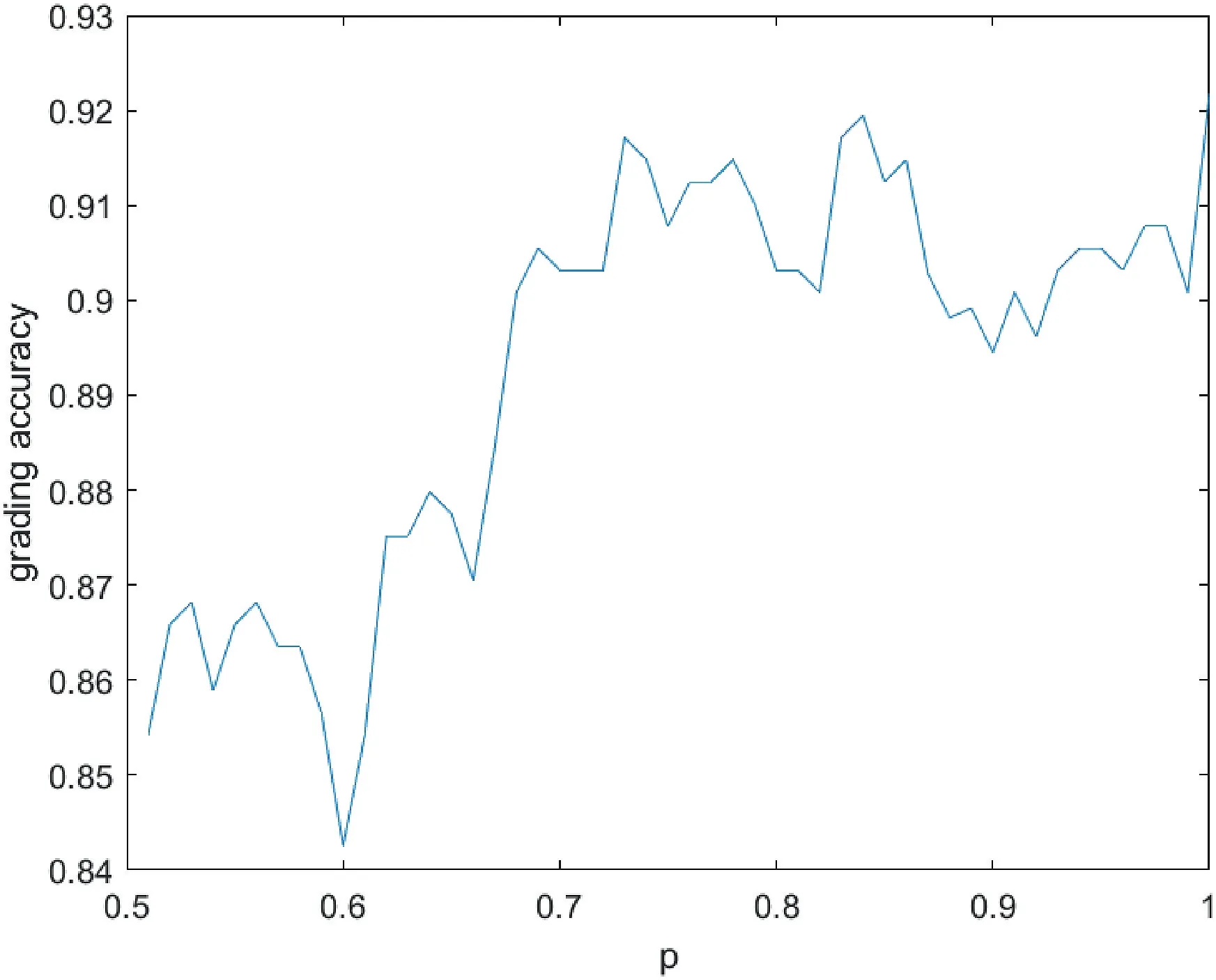
4.1|Selection of model parameters
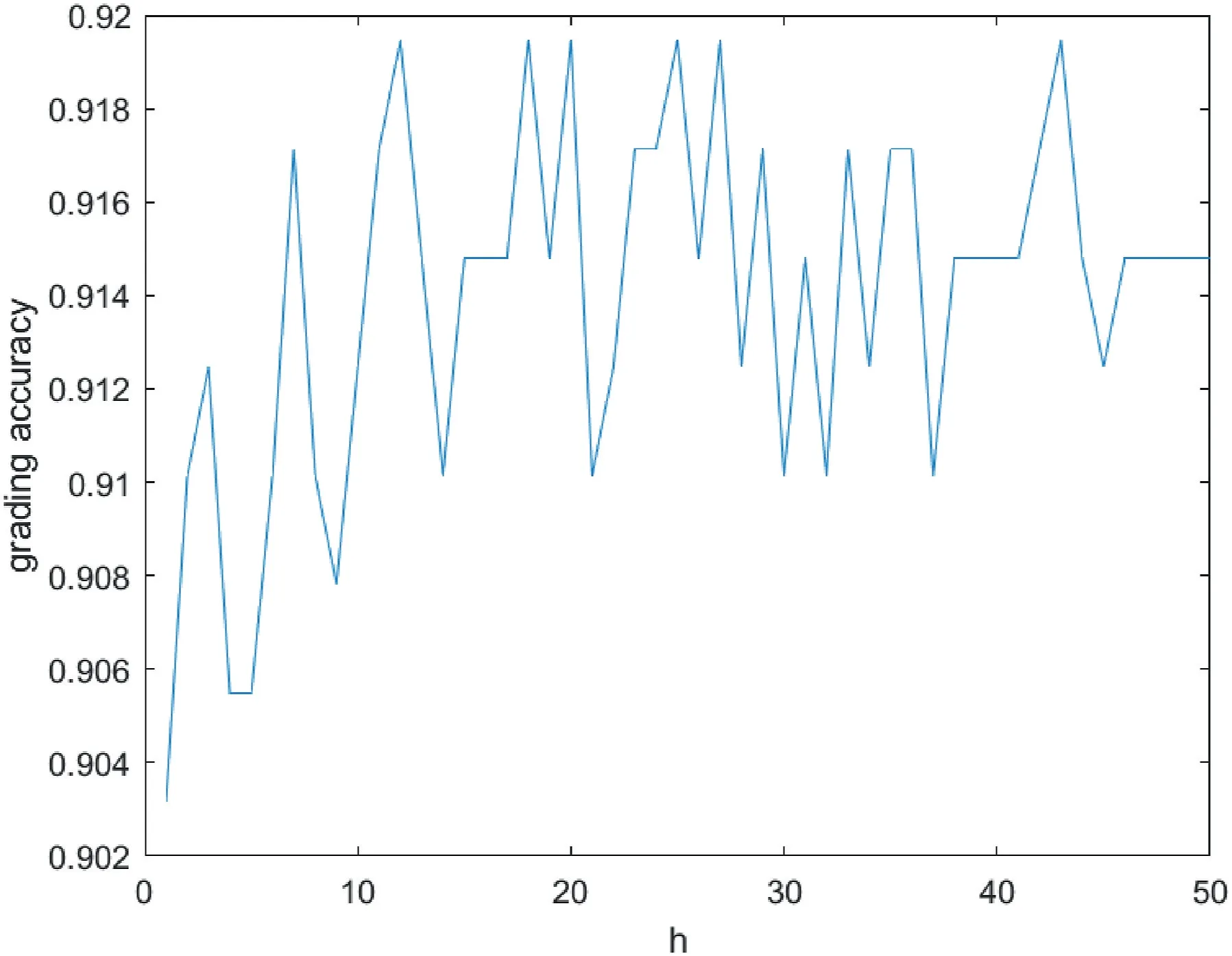

4.2|Performance comparison
5|CONCLUSION
 CAAI Transactions on Intelligence Technology2022年4期
CAAI Transactions on Intelligence Technology2022年4期
