方向性脉冲型地震动对沉管隧道动力响应分析
张钰琦,汪俊诚,吴勇信
(河海大学 土木与交通学院, 江苏 南京 210098)
自20世纪以来,沉管隧道因其适应性强、埋置浅、航运干扰小、防水性能好等优势,已在全世界作为穿越江河、港湾、海底的重要交通设施。沉管隧道大多数修建于水域软弱地层中,周围受到土体的约束,在地震作用下,其动力响应相对于地面结构较为柔和,被认为相对不易受到破坏,导致其地震响应分析研究较晚[1]。但由于沉管隧道所处位置相对特殊,一旦发生震害,将难以修复,因此吸引了不少学者对于沉管隧道的抗震分析。常见的沉管隧道抗震分析方法有数值模拟和模型试验。袁勇等[2-4]以港珠澳大桥沉管隧道为工程背景,开展了沉管隧道的振动台模型试验,研究得出沉管隧道的管节加速度响应及接头最大张开量,提出隧道关键节点的减震控制方法。闫维明等[5-6]通过沉管隧道的振动台试验,关于沉管隧道减震进行了研究。陈贵红等[7-8]、曾朗杰[1]及程新俊[8]采用有限元软件分别对沉管隧道进行了二维和三维模型的动力响应分析,研究得出在水平地震作用下,沉管隧道的动力响应受水的影响不大,且提出了耗能减震式局部沉管隧道接头。Miao等[9]基于Davidenkov骨架曲线的土体非线性动力粘弹性本构模型,分别对武汉三阳路跨江隧道工程和汕头苏埃隧道工程进行模拟,发现土体动力特性和场地非均匀性对不同激励地震动作用下的结构响应影响很大,并且近场地震动对隧道结构响应更大,造成破坏更严重。近断层地震的方向性效应和滑冲效应是产生速度脉冲的主要原因。目前近断层脉冲型地震动对结构的响应已受到许多学者研究,李帅等[10-11]以苏通大桥斜拉桥为研究对象,得出脉冲速度峰值、奇数个脉冲数及有脉冲型地震动对结构响应更显著的规律。宋健等[12]通过研究近断层地震动作用下的土质边坡动力响应,发现速度脉冲型地震动对边坡的破坏作用远强于无速度脉冲型地震动。朱育才等[13-15]研究发现近断层地震动作用下对隧道的动力响应与远场地震动相比,会产生更大的应力、位移响应。
以上研究从原理、试验方法和数值分析上得到沉管隧道响应规律,提出了减震方法;在上部结构、土质边坡以及隧道结构中都有考虑具有长周期、大幅值、短持时的脉冲特性地震动的影响,这种地震动相对于普通地震动对结构的响应大的多,破坏也严重的多[16]。而在沉管隧道的研究上考虑脉冲型地震动对其动力响应分析的影响几乎没有,并且未保证所选的有无速度脉冲地震动的同源性及反应谱的相似性。本文基于Davidenkov骨架曲线的土体非线性动力粘弹性本构模型,采用ABAQUS软件建立了沉管隧道的有限元模型,再通过MATLAB对地震动数据进行处理,一方面可以得到所选站台水平两条正交方向的最大合成加速度时程,另一方面对地震动中速度脉冲进行提取。主要研究分析由方向性效应引起的双向速度脉冲地震动(forward directional pulse groud motions,FD)及相应剔除速度脉冲的无脉冲地震动(non-pulse ground motions,NP)作用下对沉管隧道的动力响应(位移、加速度、应力),研究结果为近断层区域沉管隧道的抗震提供一定的参考。
1 沉管隧道地震响应数值模拟
1.1 模型建立及参数选取
三维数值模型的建立不仅工作量巨大,并且所占电脑内存更多,模型尺寸及网格划分大大限制了其计算速度,根据张国强[17]的研究发现将三维结构模型简化为二维模型的计算结果相差不大,因此本文以广州佛山市沉管隧道[1]为参考采用ABAQUS有限元软件建立了二维的沉管隧道模型。模型设计以公路段为双向四车道三孔的箱型结构,单跨结构净宽8.65 m,中间设净宽为1.5 m的电缆廊道。沉管段标准横断面宽为23 m,高度为9 m,管节横断面如图1。

图1 沉管隧道横断面图Fig.1 Cross-section view of immersed tunnel
采用有限元软件进行计算分析时,需对模型边界进行一定近似的有界处理。目前动力计算分析中比较常用的为黏弹性边界[18],其稳定性良好并且精度较高,但其计算效率低,对于批量工况的计算实属不易,并且其占用内存较高,大多用于均质土体的边界设置,对于多层土适用情况有待研究。因此为了尽可能消除边界影响,在时间域内求解非线性问题,只能把边界取得尽可能远一些来实现[19]。根据楼梦麟等[20]的研究表明,当地基侧向宽度与地下结构宽度之比大于5倍时,可以忽略边界效应带来的影响。因此本文有限元模型取左右对称,地基宽度取500 m,竖向取60 m,两侧边界为自由边界,底部为固定边界。土层参数如表1。沉管隧道及周围土体采用四结点平面应变实体单元模拟,并且隧道结构简化为弹性体进行计算,参数如表2。

表1 土层参数Tab.1 Soil parameters

表2 沉管隧道参数Tab.2 Structural parameters of immersed tunnel
1.2 材料的动力非线性本构
本文采用基于Davidenkov骨架曲线的土体非线性动力粘弹性本构模型[21-23]。Davidenkov模型是由Martin等人通过提出三参数A、B和γ0去拟合各类土体的动剪切模量比G/Gmax-γ曲线的实验结果的方法,基于此方法的骨架曲线建立了一维加卸载应力-应变关系为:
(1)
该式描述了当施加的应力转向后,后续的应力-应变曲线沿当前拐点指向历史最大(小)点的方向前进,应力-应变滞回曲线由初始骨架曲线放大n倍来构造,代替了Masing法则中的放大倍数2。
式中τc、γc别为应力-应变滞回曲线加卸载转折点对应的应力和应变;Gmax最大剪切模量;H为描述应力-应变关系的基本形状函数;参数n分别取1和2,代表初始加载和卸载情况。
在对沉管隧道进行非线性动力反应分析时,定义其周围土体和岩石的应力-应变关系通常用八面体的应力-应变关系,通过瑞利阻尼的概念定义黏性阻尼阵来考虑土体材料的黏性效应,并且假设阻尼矩阵只与刚度矩阵有关,可以定义最终的应力-应变关系为:
(2)
式中:α1为瑞利阻尼系数;Del为初始弹性刚度矩阵。
本文采用隐式积分求解非线性动力问题,编制Jacobi矩阵∂Δσ/∂Δε,在每一时步结束时都按(2)式进行应力更新。
2 脉冲地震动参数选取
近断层一般表示断层距小于20~60 km之间[24-25]。为分析近断层方向性速度脉冲型地震动对沉管隧道的地震响应,本文基于Shahi所记录的243条脉冲型地震动数据,其中具有方向性效应的地震动与断层距分布关系如图2,可见大部分具有方向性效应的地震动的断层距小于30 km,从中选择40组作为计算的脉冲地震动数据。图3以NGA_182地震动为代表描述了方向性脉冲效应的地震动加速度、速度及位移时程曲线。由图可知,该地震动具有明显的速度和位移脉冲,而且脉冲曲线呈双向往复形式,地震动最终位移趋向于0。

图2 方向性脉冲地震动断层距分布图Fig.2 Fault distance distribution map of directional pulse ground motion
地震发生在空间和时间域上均具有高度的不确定性。通常地震动加速度记录仪监测到的地震动在空间上会被分解成三条两两互相垂直的分量:两条水平分量和一条竖直分量,已有研究[26]通过水平方向上两条正交的地震动分量定量分析脉冲效应的方向性,对于同一站台记录的脉冲地震动在两条水平地震动分量上可能不都具备方向性,因此按照式(3)对其按照平行四边形法则进行合成,可以得到任意方位角的地震动[27]。
α(t;θ)=α1cos(θ)+α2sin(θ)
(3)
式中:α(t;θ)为对应θ方向的地震动加速度时程;α1、α2为原始地震动所记录的两条加速度水平分量;θ为在原始地震动记录的基础上旋转的角度。
本文以正北方向为0°,按顺时针变化,通过以每1°进行旋转,得到最大合成PGA的地震动加速度时程及其方位角,判定其具有明显的脉冲效应,同时为了对比分析有无脉冲型地震动作用下结构的响应,不可忽略地震动时程具备同源性和反应谱相似性的特性[28]。因此采用LSF法[26]对脉冲进行提取,可以得到与FD地震动同源但不含速度脉冲的NP地震动,经过处理的NP地震动在长周期段是不含有速度脉冲成分。已有研究近场地震动作用下基于非线性时程分析地下结构的地震动强度参数,以地表峰值加速度作为地震动强度指标更适合于预测结构在地震作用下的动力响应[29-30]。因此本文分析近场方向性脉冲型地震动对沉管动力响应的数值计算时,将输入地震波PGA均调整为0.3 g。所选40组脉冲地震动基本信息见表3,表中R为峰值速度影响系数,即PGV_FD/PGV_NP比值,反映的是FD地震动和NP地震动在PGV上的差异,该值越大表明差异越大。
图4对40组地震动的加速度反应谱进行分析,从中可以看出,在中长周期部分,FD地震动较于NP地震动存在有明显的脉冲,并且在高频部分,两者几乎重合。
图5从40组地震动中选择4组地震动为代表进行加速度反应谱分析,从图中可以看出,通过LSF法除去速度脉冲后,NP地震动的加速度反应谱除了在长周期段与FD地震动有所不同外,其余地方基本相似,并且脉冲部分均在脉冲周期的附近周期段,满足了同源性和反应谱相似性。

图3 方向性效应脉冲地震动(NGA_182)Fig.3 Directional effect pulsed ground motion (NGA_182)
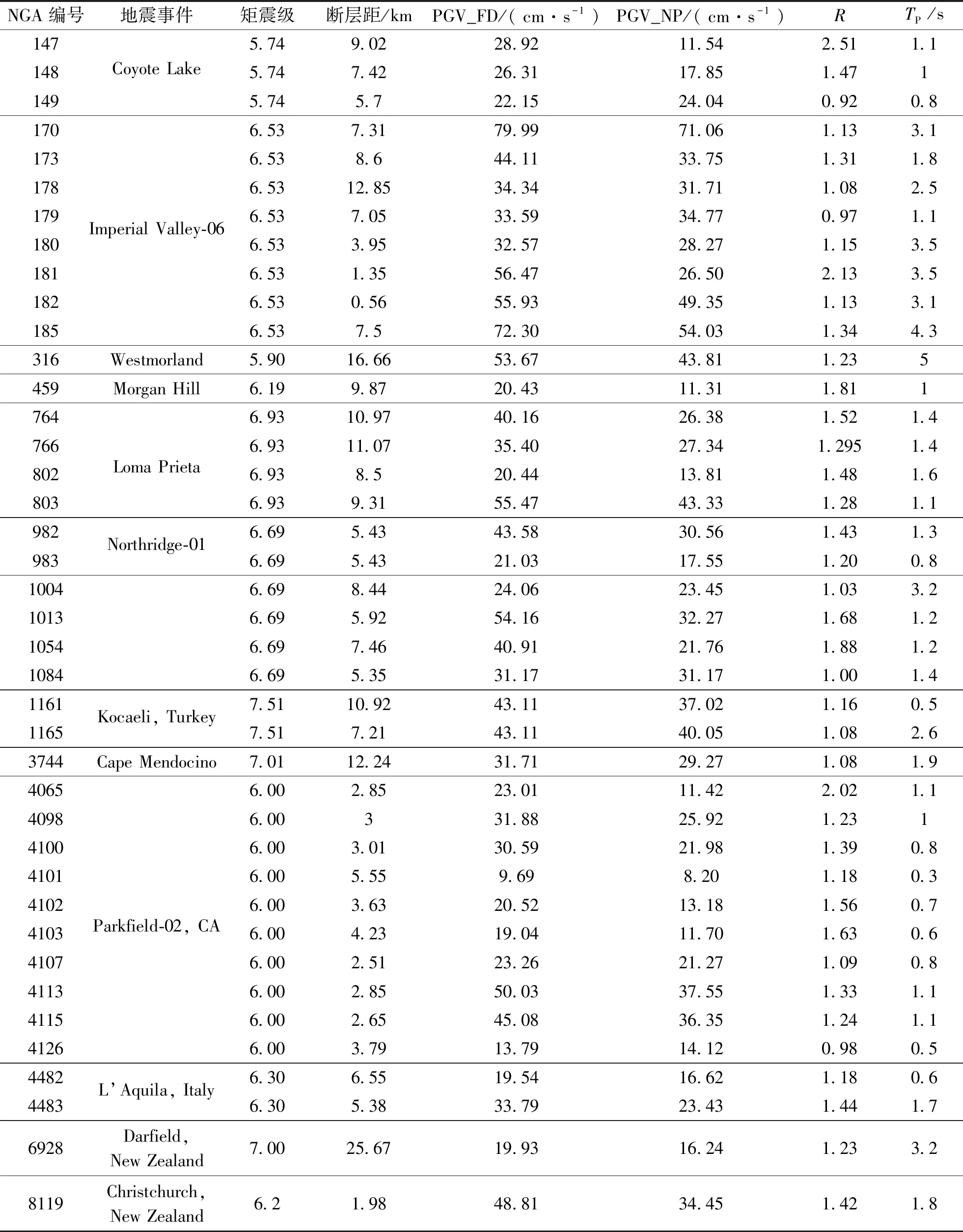
表3 地震动特性参数Tab.3 Ground motion characteristic parameters
3 计算结果分析
本文由频率分析步先计算出结构的自振周期,取其第一阶自振周期结果T1,T1=0.972 3 s。将选定的FD地震动与NP地震动共80组地震动输入沉管隧道进行地震响应分析,主要分析FD、NP地震动在不同峰值速度及脉冲周期下的沉管隧道加速度、位移及其应力响应的影响。定义位移反应脉冲影响系数为KU,沉管底部和顶部加速度反应脉冲影响系数分别为KA_bot和KA_top以及应力反应脉冲影响系数为KS,相应计算公式如下:

图4 40组地震动加速度反应谱Fig.4 40 sets of ground motion acceleration response spectrum
(4)
(5)
(6)
式中:UFD、UNP分别为FD、NP地震动作用下沉管隧道位移响应的最大值;Abot_FD、Abot_NP、Atop_FD、Atop_NP分别为FD、NP地震动作用下沉管底部、顶部加速度响应的最大值;SFD、SNP分别为FD、NP地震动作用下沉管应力响应的最大值。
3.1 位移响应分析
由于沉管隧道的结构对称,通过提取左、右墙的底、顶部之间的水平向相对位移时程,发现数据相差较小,因此仅对隧道左墙的相对水平位移进行分析。图6中显示4组代表性地震动作用下,最大相对水平位移时刻的沉管隧道侧墙随高度的相对水平位移变化。由图可知,左墙相对水平位移随高度的变化曲线接近于双曲线,并且FD地震动产生的相对水平位移要大于NP地震动。
图7反映了40组FD、NP地震动输入沉管隧道的位移响应,提取结构左墙相对水平位移的最大值,随着PGV的增大,FD、NP地震动作用下左墙相对水平位移都呈现出增大趋势,并且FD 地震动产生的相对水平位移要大于NP地震动;图8揭示了峰值速度影响系数R对隧道位移响应的影响,可见随着R的增大,KU也呈现出增大趋势,表明地震动存在速度脉冲会增大沉管隧道的位移响应;图9呈现了脉冲周期对隧道位移响应的影响规律,研究发现,随着脉冲周期的增大,KU呈现出先增后减趋势,并且脉冲周期在结构第一阶自振周期附近区间时,KU值较大,说明此时脉冲周期对沉管隧道位移响应影响较大。

图5 4组代表性地震动加速度反应谱Fig.5 Four groups of representative ground motion acceleration response spectra

图6 4组地震动作用下沉管隧道侧墙随高度的相对水平位移Fig.6 Relative horizontal displacements of the side walls of immersed tunnels with height under four groups of ground motions

图7 PGV对沉管隧道的相对水平位移影响Fig.7 PGV affects the relative horizontal displacement of immersed tunnel
3.2 加速度响应反应
图10、图11分别给出了4组代表性FD、NP地震动作用下沉管隧道结构底部、顶部的水平加速度反应时程。从图中可知:FD、NP地震动作用下沉管隧道的加速度时程上大部分处于重合,FD地震动作用下沉管隧道的PGA要大于NP地震动,且隧道顶部的PGA都要比隧道底部大,可见地震动存在速度脉冲时,对沉管隧道的加速度响应都有一定的增大。

图8 R对沉管隧道位移响应影响Fig.8 Influence of R on displacement response of immersed tunnel

图9 Tp对沉管隧道位移响应影响Fig.9 Influence of Tp on displacement response of immersed tunnel

图10 4组地震动沉管隧道底部的加速度时程Fig.10 Acceleration time history of the bottom of four groups of ground motion immersed tunnel

图11 4组地震动沉管隧道顶部的加速度时程Fig.11 Acceleration time history of the top of four groups of ground motion immersed tunnel

图12 PGV对沉管隧道峰值加速度影响Fig.12 Influence of PGV on peak acceleration of immersed tunnel

图13 R对沉管隧道加速度响应影响Fig.13 Influence of R on acceleration response of immersed tunnel

图14 Tp对沉管隧道加速度响应影响Fig.14 Influence of Tp on acceleration response of immersed tunnel
图12反映了40组FD、NP地震动作用下沉管隧道底部和顶部的峰值加速度响应结果,随着PGV的增大,沉管隧道底部、顶部的峰值加速度也增大,并且FD地震动作用下产生的峰值加速度要大于NP地震动(黑点部分整体偏高于红点部分);图13揭示了峰值速度影响系数R对隧道加速度响应的影响,随着R的增大,KA_bot、KA_top也都呈现出增长的趋势,其中R值越大,FD地震动和NP地震动的响应相差也大,表明地震动中存在速度脉冲会增大沉管隧道的加速度响应;图14呈现了脉冲周期对隧道加速度响应的影响规律,研究发现,随着脉冲周期的增大,KA_bot、KA_top表现为先增后减的趋势,并且脉冲周期在结构第一阶自振周期附近区间时,加速度反应脉冲影响系数值较大,说明此时脉冲周期对沉管隧道的加速度响应影响较大。
3.3 应力响应分析
图15给出了代表性地震动(NGA_182)作用下沉管隧道最大相对位移时刻的Mises应力云图,从图中可以发现,在中柱部分以及结构边角部分的应力较大,并且最大Mises应力都出现在中柱上,同时FD地震动对沉管响应产生的最大Mises应力(14.41 MPa)都大于NP地震动(12.17 MPa)。
图16反映了40组FD、NP地震动作用下沉管隧道的最大Mises应力响应,随着PGV的增大,沉管隧道的应力响应也增大,并且FD地震动作用下产生的应力响应要大于NP地震动;图17呈现了峰值速度影响系数R对隧道应力响应的影响,随着R的增大,KS也都呈现出增长的趋势,其中R值越大,FD地震动和NP地震动的应力响应相差也大,表明地震动中存在速度脉冲会增大沉管隧道的应力响应;图18揭示了脉冲周期对隧道应力响应的影响规律,研究发现,随着脉冲周期的增大,KS表现为先增后减的趋势,并且脉冲周期在结构第一阶自振周期附近区间时,应力反应脉冲影响系数值较大,说明此时脉冲周期对沉管隧道应力响应影响较大。

图15 沉管隧道应力云图(NGA_182)Fig.15 Stress nephograms of immersed tube tunnel (NGA_182)

图16 PGV对沉管隧道应力影响Fig.16 Influence of PGV on stress of immersed tunnel

图17 R对沉管隧道应力响应影响Fig.17 Influence of R on stress response of immersed tunnel

图18 Tp对沉管隧道应力响应影响Fig.18 Influence of Tp on stress response of immersed tunnel
4 结论
1)随着地震动PGV的增大,FD、NP地震动对沉管隧道的位移、加速度和应力响应都呈现出增长的趋势,并且FD地震动相对于NP地震动作用下对沉管隧道的响应要大,具体体现在:FD地震动作用下产生的沉管隧道左墙相对水平位移、结构底部及顶部的加速度峰值、提取最大相对位移时刻的Mises应力都要更大。
2)峰值速度影响系数R越大,说明FD、NP地震动的PGV相差越大。随着R的增大,沉管隧道各响应的脉冲影响系数也呈现增大趋势,表明地震动中存在方向性速度脉冲对结构响应的影响更大,因此在结构抗震中考虑地震动的速度脉冲效应很有必要。
3)随着脉冲周期的增大,位移、加速度和应力响应的脉冲影响系数都表现为先增后减的趋势,并且脉冲周期在结构第一阶自振周期附近区间时,各响应脉冲影响系数值都较大,表明此时FD地震动作用下相对于NP地震动对沉管隧道的破坏更大。

