实时高精度雷达噪声信号产生方法与FPGA实现*

蔡俊晖,潘明海

(南京航空航天大学 电子信息工程学院 雷达成像与微波光子技术教育部重点实验室,南京 211106)

0 引 言

使用数字射频存储器(Digital Radio Frequency Memory,DRFM)对雷达系统进行半实物仿真时,除了需要模拟雷达探测真实目标的回波信号外,各种服从复杂函数分布的噪声信号、干扰信号,以及杂波信号也是雷达回波信号中重要的一部分[1-2]。

信号在传输过程中易受雷达系统内外部噪声和环境杂波的干扰,从而影响雷达系统性能,而雷达噪声信号干扰和杂波模拟的实质就是要求产生具有一定概率分布和功率分布的相关序列[2]。

噪声信号同样在噪声雷达的波形设计中应用广泛[3-5],使用噪声信号波形作为雷达探测信号具有很强的抗干扰性和低截获性。因此考虑到噪声信号在雷达系统应用中的实际需求,快速产生高精度、服从多种函数分布噪声信号具有重要意义。由于现场可编程技术的发展,基于硬件的噪声信号生成方法因其相比软件生成方法具有巨大优势而受到广泛关注。本文提出了一种基于现场可编程逻辑器件(Field Programmable Gate Array,FPGA)的实时高精度噪声信号产生方法,与其他文献相比,在占用较少硬件资源的情况下能够快速产生多种不同分布的高精度随机噪声序列,不仅可以用来模拟信号传输过程中的噪声和杂波信号,同时由于其实质是按照一定算法产生的伪随机序列,也为噪声雷达信号波形的设计提供了选择。

1 典型分布的噪声特点与产生原理

复杂分布噪声存在于雷达系统各个环节。雷达接收的真实回波信号x(t)可由公式(1)给出:

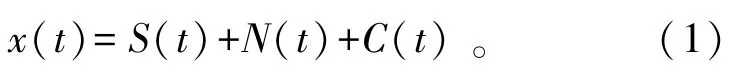
式中:S(t)为散射回波;N(t)为噪声;C(t)为杂波。高斯噪声是雷达系统中最普遍的噪声,接收机内外部噪声以及地杂波起伏特性一般都符合高斯分布。杂波的统计特性多种多样,一般有瑞利分布、对数正态分布、K分布等[6]。本文实际产生了五种典型分布的随机序列,分别是均匀分布随机序列、指数分布随机序列、高斯分布随机序列、瑞利分布随机序列以及莱斯分布随机序列。

在FPGA上产生的随机序列可以分为真随机序列和伪随机序列。真随机序列可以满足任何随机性的统计检验,但是在FPGA上产生真正的随机序列是十分耗费时间和资源的。伪随机序列看起来是随机的,但其实这种序列是由某种特定的算法生成,仍然具有一定的重复周期,但当重复周期非常大时,雷达脉冲周期与其相比可以认为这种伪随机序列是随机、不具备周期性的。

1.1 基于LFSR的均匀分布随机序列产生

线性反馈移位寄存器(Linear Feedback Shift Register,LFSR)是FPGA中产生均匀分布伪随机序列常用的一种工具。典型的4位LFSR硬件结构如图1所示,通过逻辑门电路设定图中的反馈支路,该4位寄存器可以遍历除四位全为0以外的其他4位二进制序列,并且每个序列在一个周期内只出现一次。因此可以增加LFSR的位数,产生周期更长的伪随机序列,N位LFSR的最长序列周期是2N-1。利用上述结构,设计两个32位的LFSR。FPGA时钟工作频率f为312.5 MHz,因此两个32位LFSR的周期为232×232×1/f≈683 217天,远大于雷达的脉冲周期,可以认为产生的伪随机序列是“真随机”的,因此在下文中提到的均匀随机序列都将认为是真随机序列。

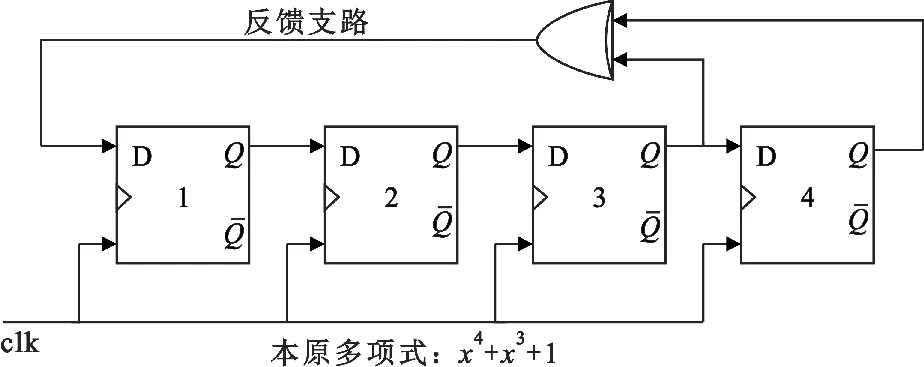
图1 四位LFSR的硬件结构

32位LFSR易在FPGA上实现,能够产生可被认为是真随机的均匀分布随机序列,但是其32位的数据长度会急剧增加FPGA实时计算难度,尤其是乘法运算。因此必须缩小均匀随机数的数据长度来保证实时性,但不能改变数据的均匀分布特性。这里截取32位LFSR前20位来减少数据长度,将截取的数据进行数值分析。图2中展示了未截取32位LFSR和截取的20位LFSR的数据分布特性,从图中可以看出,通过此方法截取产生的均匀随机序列在延长其序列周期的情况下,其概率分布特性仍然保持了较好的均匀分布特性。

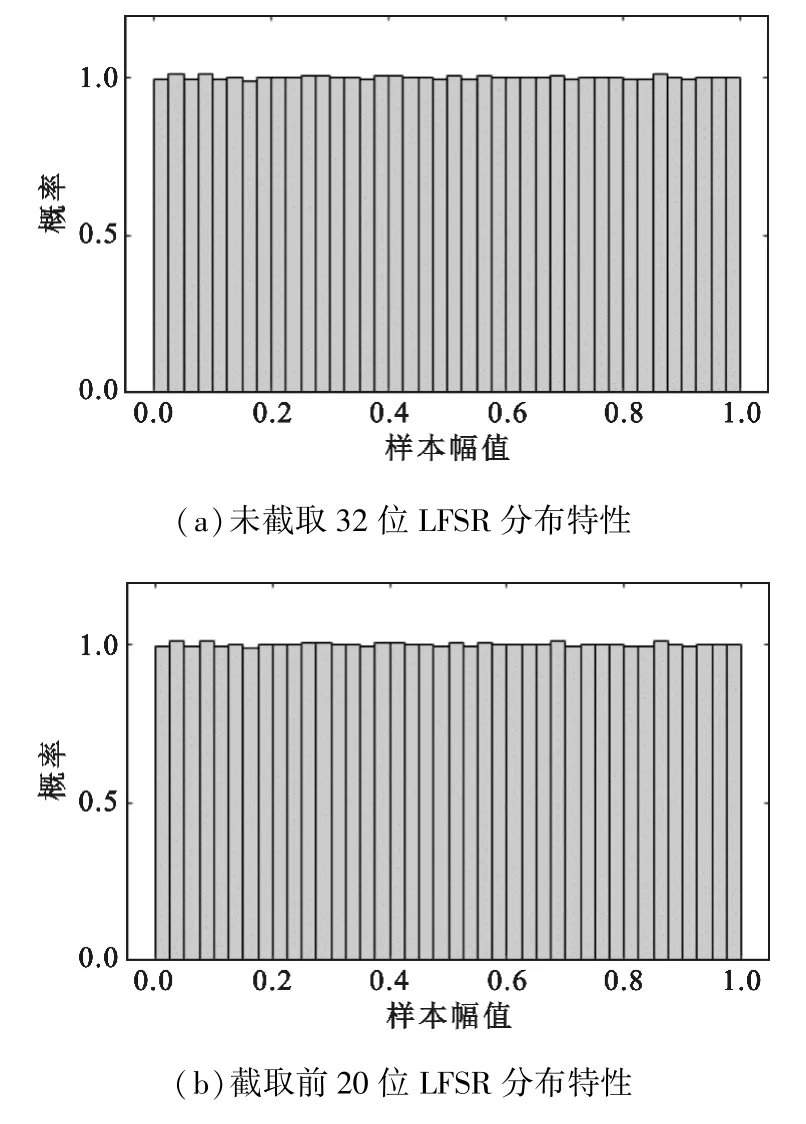
图2 未截取32位LFSR与截取20位LFSR分布特性对比

1.2 基于Box-Muller变换的高斯分布随机序列产生

FPGA便于实现定点运算,不易实现小数运算,因此直接产生服从各种复杂分布函数的随机序列是比较困难的,需要从另外的角度来考虑生成随机数据。本文从概率密度函数方面进行随机序列的生成,主要有Ziggurat算法、Wallace算法和Box-Muller算法。Ziggurat算法是一种经典的拒绝采样方法,但是其数据输出速率不是连续的,不利于硬件仿真[7]。Box-Muller算法是一种速度快、步骤少、便于硬件实现的算法,在各种文献中被广泛引用[4,9-12]。Wallace算法由于其自身反馈结构的原因,会使得部分数据之间会产生相关性。因此,本文采用了Box-Muller算法。该算法仅需通过四种数学运算就可以将均匀分布的随机数转换成服从高斯分布的随机数。该算法可由公式(2)和公式(3)表示:

式中:u0与u1是两组独立的(0,1)之间均匀分布的随机序列。将u0与u1进行上述公式中的计算,得到两组独立的均值为0、方差为1的高斯分布随机序列x0与x1,即x0～N(0,1),x1～N(0,1),其概率密度分布函数为

高斯分布的随机序列为产生瑞利分布、莱斯分布以及指数分布的随机序列提供了基础。

1.3 复杂非高斯分布随机序列的产生

根据定义:当一个随机二维向量的两个分量呈独立的、均值为0、有着相同方差的正态分布时,这个向量的模呈瑞利分布。即当且x0～N(ucosθ,σ2),x1～N(usinθ,σ2)时,则x～其概率密度分布函数为

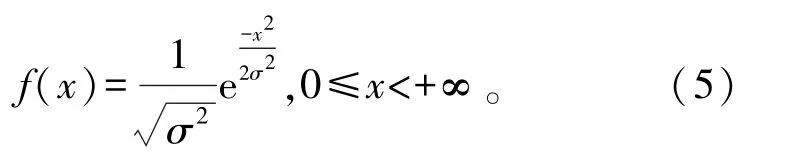
由公式(2)与公式(3)可以看出,Box-Muller算法中产生的两组高斯数据x0与x1是相互正交的,所以公式(2)或公式(3)中的计算所得的随机序列是直接服从瑞利分布的随机序列。

根据定义:当一个随机二维向量的两个分量呈独立的、均值不同、方差相同的正态分布时,这个向量的模呈莱斯分布。即当x0～N(ucosθ,σ2)且x1～N(usinθ,σ2),若,则σ2),其中u和θ为任意实数。其概率密度分布函数为

根据定义:u是服从均匀分布的随机变量,那么如果x=-ln(u)/λ,λ为任意实数,则x服从于指数分布,即x～E(λ),其概率密度分布函数为

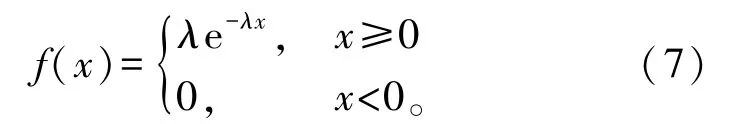
根据Box-Muller算法以及上述复杂分布函数定义,可以总结出:首先产生服从均匀分布的随机序列,通过有限的数学计算,即可得到多种服从不同分布函数的随机序列。将运算过程总结成图3所示的流程图,只需添加一个多路复用器,就可以实时切换选择不同概率分布的噪声信号输出。下文将详细介绍流程图中主要运算模块的原理以及在FPGA上的实现方法。

图3 基于Box-Muller算法流程图

2 噪声信号产生方法的FPGA实现

图3中流程主要包含对数、平方根、乘加以及三角函数四种数学计算。乘法运算以及加法运算易在FPGA上实现,而对数函数运算、平方根运算以及三角函数运算在FPGA上实现较为复杂,目前常用的方法有查表法、分段多项式近似法和坐标旋转数字计算(Coordinate Rotation Digital Computer,CORDIC)法[9]。查表法精度最高,速度最快,但由于本文计算精度都非常高,如果使用查表法必然会耗费大量存储资源。分段多项式的硬件实现较为复杂,需要使用多级乘法器,会带来较大的延迟,不利于信号的实时计算。CORDIC算法是一种用于计算复杂函数的循环迭代算法,用一系列与运算基数相关角度的不停摆动,逼近所需旋转的角度,将复杂的算法分解成加法、移位等易在硬件上实现的操作。因此为了能完成复杂函数的快速计算,降低延迟,提高系统的实时性,本文选择使用CORDIC算法。CORDIC IP核是FPGA开发软件提供的IP核,利用CORDIC算法能够实现平方根、正余弦以及反双曲正切函数的计算,但CORDIC IP核对数据的输入范围有严格要求,超过输入范围外的数据会得到错误的数据,因此在实时计算时需要对输入的数据进行调整来满足输入要求,以便得到高精度的计算结果。

2.1 对数函数的FPGA高精度实时运算

对数函数运算不能直接用CORDIC算法来实现,考虑到双曲正切函数的表达式为

因此其反函数为

令

将其带入式(9),可得

因此可以利用这个等式来实现Box-Muller算法中第一步的对数计算。设置两个新的变量t1=x-1和t2=x+1,x是LFSR产生的在(0,1)之间均匀分布随机序列1,最小值为2,对应的对数函数值-13.863。但是由于CORDIC IP核能够正确计算双曲正切函数的数据输入范围是0.106 85＜x＜2,因此需要对第一步产生的均匀分布随机序列进行放大,如式(12)所示:

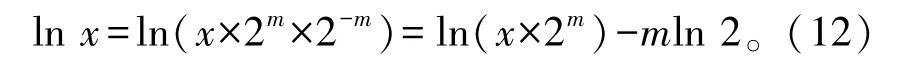
式中:m是使数据左移到数据的小数点后第一位为1的正整数。此时,CORDIC IP核能够正确计算出放大后数据的函数值,最后减去mln 2即可得到正确的原输入数据的对数函数值。通过此方法进行对数运算,得到5位有符号整数位、20位小数位的二进制补码数据,其数值范围是[-13.86,0]。

2.2 平方根函数的FPGA高精度实时运算

CORDIC算法同时能实现求平方根的运算。将对数运算计算出的值乘-2,得到的随机序列数值范围为[0,27.72],但是由于CORDIC IP核只能正确计算[0,2)范围内平方根的运算,因此需要对输入数据进行缩小,否则直接计算会得到错误数据,如式(13)所示:

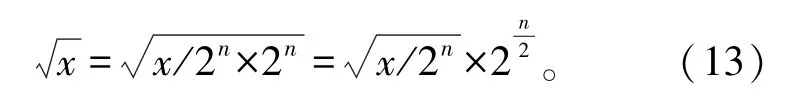
由于需要计算的数值范围是[0,27.72],整数部分需要5位二进制数来表示,因此将数据左移4位后即可得到[0,2)的数据,带入求出平方根数值,最后再将求出数据的右移两位即可,得到无符号3位整数位、20位小数位的二进制补码数据,其数值范围是[0,5.265]。

2.3 其他函数FPGA高精度实时运算

CORDIC算法最易实现三角函数的计算。将产生的均匀分布随机序列2与2π相乘,得到[0,2π]内随机分布的相位。CORDIC IP核相位输入要求是[-π,π],因此需要对随机分布的相位进行调整。根据三角函数的性质,对于相位在[π,2π]的随机相位,只需要减去2π然后进行三角计算即可得到正确的三角函数值。通过此方法计算得到2位有符号整数位、20位小数位的二进制三角函数值,其数值范围是[-1,1]。

本文中,所有函数计算的数据都保留到二进制小数位20 b(9.536×10-7)来保证数据精度,避免影响生成数据的分布特性,同时20位的小数精度能够根据需求自适应调节DAC芯片输入有效位数,产生相对幅度不同的噪声信号。实现上述高精度计算模块之后,利用握手信号来同步随机序列在各模块之间连续计算,以此来提高信号实时产生速率。

3 噪声信号实时产生方法的仿真与实验

噪声信号实时发生器的结构如图4所示。噪声发生器根据上位机的指令实时产生五种分布的随机序列,同时脉冲发生器可以根据需求产生脉冲回波信号或者连续信号,进而产生服从复杂分布噪声的雷达回波信号,为雷达性能测试和噪声雷达波形设计提供目标信号。

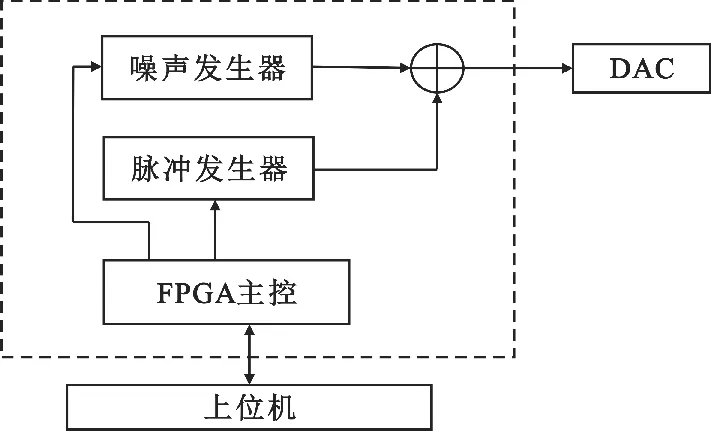
图4 实时噪声信号产生框图

FPGA芯片使用了Xilinx XC7VX415T,此款芯片足以满足本设计的需要。利用Verilog HDL语言实现上述所有功能模块,然后按照图3的处理流程在FPGA上进行综合。设置图3中的参数λ=1、v=0、u1=u2=0或u1=0.8、u2=0.6。用Isim软件监视仿真生成的数据,如图5所示。从图中可以看出,基于本文的快速实时算法在上位机下达的使能信号有效后,立即得到红色服从均匀分布的随机序列,30个时钟周期得到灰色服从指数分布的随机序列,60个时钟周期后得到黄色服从高斯分布的随机序列,90个时钟周期之后得到蓝色服从瑞利(u1=u2=0)或莱斯(u1=0.8,u2=0.6)分布的随机序列。整个算法延迟低,实时性高。

图5 仿真生成的四种随机信号序列

在DRFM开发板上进行试验。FPGA芯片频率工作在312.5 MHz,通过8路并联的方法,噪声信号实时产生速率可达2.5 GHz,与DAC芯片工作频率一致。如有需要,可以通过并行更多通道数实现更高速度的数据实时产生速率。算法硬件开发平台如图6所示。

图6 DRFM开发板卡

由于均匀分布序列的特性前文已经给出,这里使用Chipscope Pro抓取后四种分布数据各106个,图7给出了各种分布数据样本的幅度图。

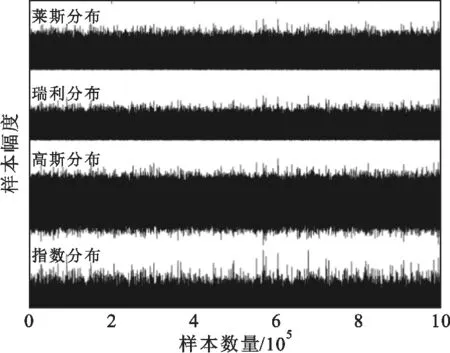
图7 数据样本幅度图

4 产生噪声信号的精度与分析

在数字系统中,数值需要被量化到有限精度,因此在本文中,数据位数的截断会带来量化误差。均匀分布小数位的精度决定了各种分布噪声的最大值,均匀分布序列的最小值为2-20,则理论高斯噪声最大值为5.26σ,其中σ为高斯分布的标准差,这是误差的主要来源。

为了评估生成随机序列的概率密度分布情况和误差,首先利用Matlab将采集到的数据进行分析,图8～11中分别使用直方图展示了硬件产生的指数分布、高斯分布、瑞利分布和莱斯分布随机序列的概率分布情况,同时在每幅图中拟合了各种概率密度函数理想情况下的曲线。可以看出,本文方法产生的复杂函数分布的随机序列直方图能够精准地符合理想的四种复杂函数的概率密度函数(Probability Density Function,PDF)。

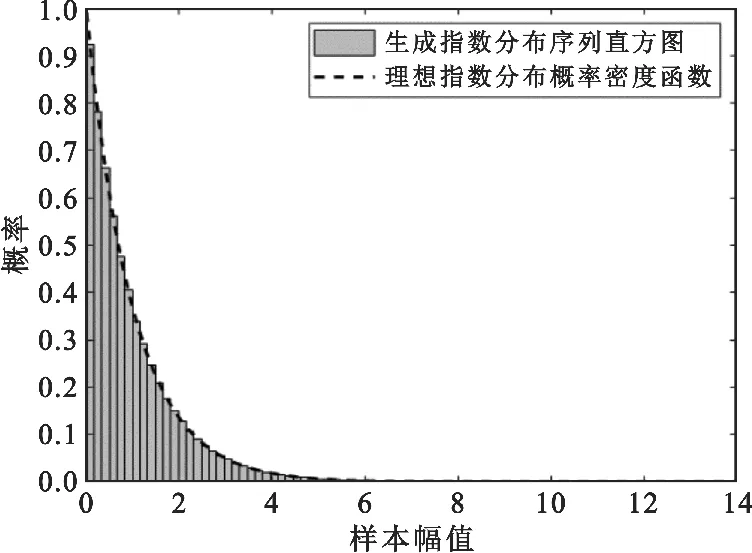
图8 产生指数分布序列样本与理想指数分布PDF对比

图9 产生高斯分布序列样本与理想高斯分布PDF对比

图10 产生瑞利分布序列样本与理想瑞利分布PDF对比

图11 产生莱斯分布样本与理想莱斯分布PDF对比

对生成四种序列的均值和方差进行分析并与理想情况下的均值和方差进行对比,结果如表1所示。从表中可以看出,生成的四种随机分布序列的均值与方差均的误差均优于0.1%,数据精度高。

表1 生成数据误差分析

所提方法的算法流程综合后硬件资源占用情况与其他文献对比如表2所示。文献[11]仅能产生高斯分布序列,应用场景有限。相比文献[4]多产生莱斯分布序列,本文在产生多种分布随机序列的情况下整体资源利用率更低,并且本文给出了具体的实时产生速率,最迟90个时钟周期就能得到多种服从复杂函数分布的随机序列,因而具有较高的实时性。

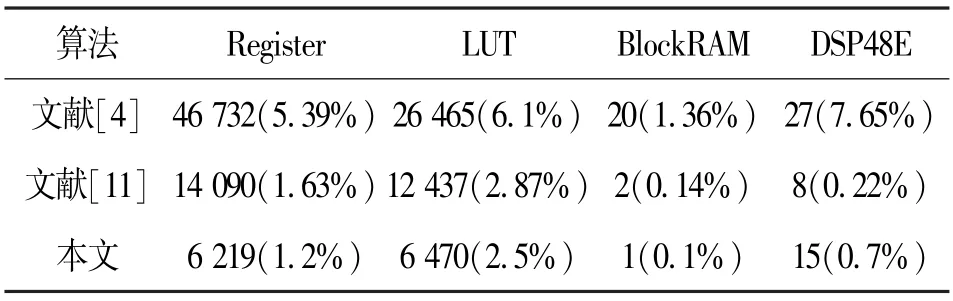
表2 硬件资源占用情况

5 结 论

本文提出了一种基于FPGA的高精度雷达噪声信号产生方法,重点阐述了不同函数分布噪声信号的产生原理以及高精度复杂函数的实时高精度计算方法,并对该方法的实际效果进行了实验验证。实测结果表明,本文提出的方法在占用极少的FPGA资源的情况下,利用CORDIC算法完成复杂函数的快速计算,能够实时产生速率为2.5 GHz的多种高精度复杂函数分布随机信号,为DRFM系统进行雷达回波仿真提供高精度噪声信号,操控简单,可用于测试雷达系统在不同噪声干扰以及杂波环境下的性能检测或噪声雷达波形设计,具有广阔的应用前景。后续将进一步研究不同幅度以及不同类型噪声对DRFM系统模拟雷达回波性能的实际影响。